手撕数据结构02--二分搜索(附源码)
一、理论基础
二分搜索,也称折半搜索、对数搜索,是一种在有序数组中查找某一特定元素的搜索算法。
二分搜索是一种高效的查找算法,适用于在已排序的数组中查找特定元素。它的基本思想是通过不断将搜索区间对半分割,从而快速缩小查找范围。
二分搜索每次把搜索区域减少一半,时间复杂度为 O(logn)(n代表集合中元素的个数)。
二分搜索的基本步骤如下:
1.初始条件:将搜索范围设为数组的整个区间。
2.查找中间元素:计算当前区间的中间索引。
3.比较中间元素:将中间元素与目标值进行比较:
- 如果中间元素等于目标值,查找成功,返回中间索引。
- 如果中间元素小于目标值,将搜索范围缩小到右半部分。
- 如果中间元素大于目标值,将搜索范围缩小到左半部分。
4.重复步骤 2 和 3,直到找到目标值或搜索范围为空。
在下图中为大家展示了二分搜索的过程:

二、代码实现
#include <iostream>
#include <vector>
using namespace std;int binarySearchRecursive(const vector<int>& arr, int left, int right, int target)
{if (left <= right) {int mid = left + (right - left) / 2; if (arr[mid] == target) {return mid;}if (arr[mid] > target) {return binarySearchRecursive(arr, left, mid - 1, target);}return binarySearchRecursive(arr, mid + 1, right, target);}return -1;
}int main()
{vector<int> arr = { 2, 3, 4, 10, 40 };int target = 10;int result = binarySearchRecursive(arr, 0, arr.size() - 1, target);if (result != -1) {cout << "元素在索引 " << result << " 处找到" << endl;}else {cout << "元素未找到" << endl;}return 0;
}相关文章:

手撕数据结构02--二分搜索(附源码)
一、理论基础 二分搜索,也称折半搜索、对数搜索,是一种在有序数组中查找某一特定元素的搜索算法。 二分搜索是一种高效的查找算法,适用于在已排序的数组中查找特定元素。它的基本思想是通过不断将搜索区间对半分割,从而快速缩小…...
单片机工程师继续从事硬件设计还是涉足 Linux 开发?
在开始前刚好我有一些资料,是我根据网友给的问题精心整理了一份「linux的资料从专业入门到高级教程」,点个关注在评论区回复“666”之后私信回复“666”,全部无偿共享给大家!!! 怎么说呢,感觉绝…...

《昇思25天学习打卡营第25天|第28天》
今天是打卡的第二十八天,实践应用篇中的计算机视觉中Vision Transformer图像分类。 从Vision Transformer(ViT)简介开始了解,模型结构,模型特点,实验的环境准备和数据读取,模型解析(…...

Flutter Dio网络请求报错FormatException: Unexpected character
最近开发Flutter项目,网络请求采用的是Dio框架,在发起网络请求的时候报错: 网络请求返回的数据为: var returnCitySN {"cip": "127.0.0.1", "cid": "00", "cname": "未…...

关于@JsonSerialize序列化与@JsonDeserialize反序列化注解的使用(密码加密与解密举例)
注:另一种方式参考 关于TableField中TypeHandler属性,自定义的类型处理器的使用(密码加密与解密举例)http://t.csdnimg.cn/NZy4G 1.简介 1.1 序列化与反序列化 学习注解之前,我们可以先了解一下什么是序列化与反序列…...

第二届世界科学智能大赛逻辑推理赛道:复杂推理能力评估 #大模型技术之逻辑推理方向 #Datawhale #夏令营 <二>
第二届世界科学智能大赛逻辑推理赛道:复杂推理能力评估 #大模型技术之逻辑推理方向 #Datawhale #夏令营-CSDN博客 这里在上一篇的基础上,已经充分理解了一遍baseline的流程,并修复了一些后处理的问题,包括答案抽取,中间…...

C# 关于Linq延迟查询
demo: int Count 0;string[] obj { "item1", "item2", "item3", "item4", "item5", "item6" };var query obj.Where(item > IsTrue(item));// 第一次遍历foreach (var item in query){Console.WriteLine(it…...

Navicat For Mysql连接Mysql8.0报错:客户端不支持服务器请求的身份验证协议
windows通过navicat连接本地mysql时报错:Client does not support authentication protocol requested by server; consider upgrading MySQL client 一、问题原因二、解决方法1--失败1. 连接mysql客户端2. 修改加密方式3.正确的解决方法1.查找my.ini文件2.修改my.ini文件3.重…...
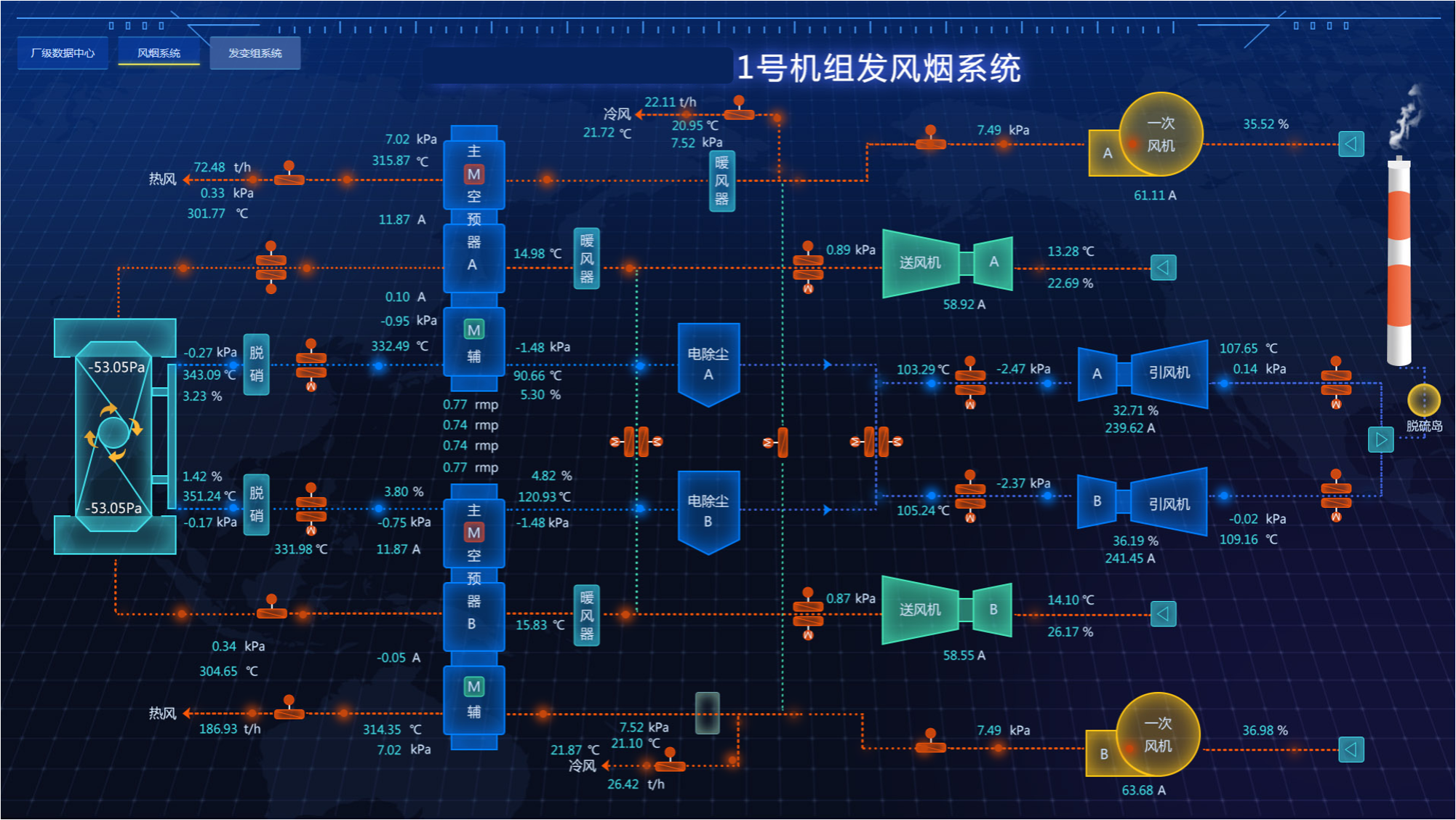
以西门子winCC为代表的组态界面,还是有很大提升空间的。
组态界面向来都是功能为主,美观和体验性为辅的,这也导致了国内的一些跟随者如法炮制,而且很多操作的工程师也是认可这重模式,不过现在一些新的组态软件可是支持精美的定制化界面,还有3D交互效果,这就是确实…...
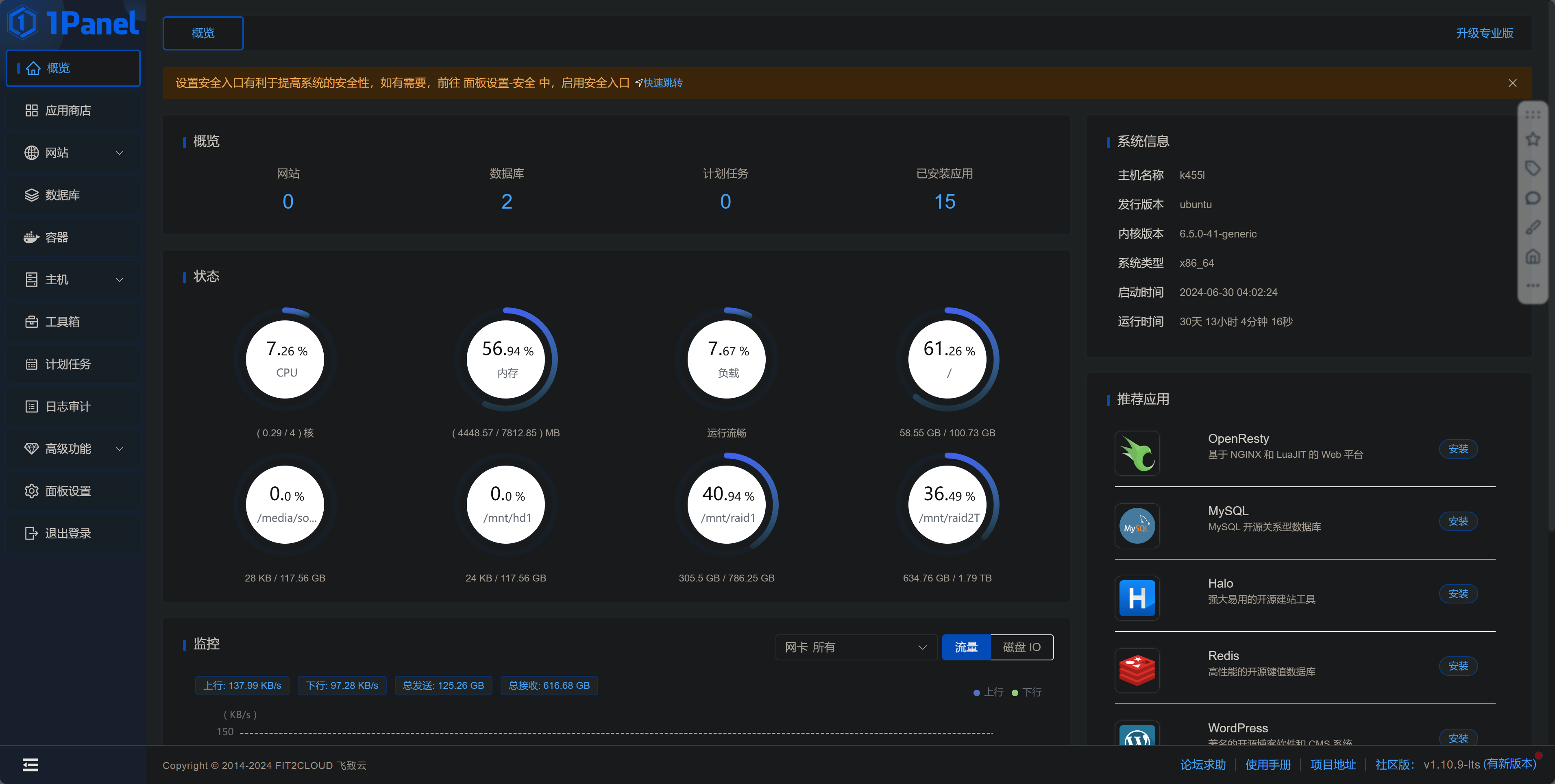
HomeServer平台选择,介绍常用功能
平台选择 HomeServer 的性能要求不高,以下是我的硬件参数,可供参考: 硬件: 平台:旧笔记本CPU:i5 4210u内存 8G硬盘:128G 固态做系统盘,1T1T 机械盘组 RAID1 做存储。硬…...

记录一个k8s集群zookeeper部署过程
由于网管中心交维要求必须是支持高可用配置,原先单节点的zookeeper不被允许。所以在k8s集群中做了一个高可用版本的zookeeper。 期间有点小波折,官方给的镜像版本太老,业务不支持,所以手动做了下处理,重新打了一个镜像…...

TapData 信创数据源 | 国产信创数据库 TiDB 数据迁移指南,加速国产化进程,推进自主创新建设
随着国家对自主可控的日益重视,目前在各个行业和区域中面临越来越多的国产化,采用有自主知识产权的国产数据库正在成为主流。长期以来,作为拥有纯国产自研背景的 TapData,自是非常重视对于更多国产信创数据库的数据连接器支持&…...

开始写人工智能
文章目录 概述 概述 开始写人工智能模块。既然决定开始写这些,那就开始吧!...

盘点.软件测试模型
软件开发模型 软件开发模型(Software Development Model)是指软件开发全部过程、活动和任务的结构框架。软件开发包括需求、设计、编码和测试等阶段,有时也包括维护阶段。 软件开发模型能清晰、直观地表达软件开发全过程,明确规定了要完成的主要活动…...

燃气安全无小事,一双专业劳保鞋让你步步安心!
燃气作为我们日常生活中不可或缺的能源之一,为我们的生活提供了极大便利,其安全性往往被忽视在忙碌的日常生活背后。然而,燃气事故一旦发生,后果往往不堪设想,轻则财产损失,重则危及生命。因此,…...

springboot校园服装租赁系统-计算机毕业设计源码30824
目 录 摘要 1 绪论 1.1 研究背景与意义 1.2国内外研究现状 1.3论文结构与章节安排 2 校园服装租赁系统分析 2.1 可行性分析 2.1.1 技术可行性分析 2.1.2 经济可行性分析 2.1.3 法律可行性分析 2.2 系统功能分析 2.2.1 功能性分析 2.2.2 非功能性分析 2.3 系统用例…...

线性回归和逻辑回归揭示数据的隐藏模式:理论与实践全解析
机器学习之线性回归和逻辑回归 1. 简介1.1 机器学习概述1.2 监督学习的定义与重要性1.3 线性回归和逻辑回归在监督学习中的作用1.3.1 线性回归1.3.2 逻辑回归 2. 线性回归(Linear Regression)2.1 定义与目标2.1.1 回归问题的定义2.1.2 预测连续目标变量 …...

掌握采购询价软件:高效比较供应商报价的技巧
在企业运营中,获取所需的产品往往是一项复杂且耗时的任务,这涉及多个环节和流程。然而,借助电子采购询价(RFQ)系统,许多原本需要采购员手动完成的任务可以自动化运行,从而提高了效率。 那么问题…...

AMQP-核心概念-终章
本文参考以下链接摘录翻译: https://www.rabbitmq.com/tutorials/amqp-concepts 连接(Connections) AMQP 0-9-1连接通常是长期保持的。AMQP 0-9-1是一个应用级别的协议,它使用TCP来实现可靠传输。连接使用认证且可以使用TLS保护…...
在WPF中使用WebView2详解
Microsoft Edge WebView2 Microsoft Edge WebView2 控件允许在本机应用中嵌入 web 技术(HTML、CSS 以及 JavaScript)。 WebView2 控件使用 Microsoft Edge 作为绘制引擎,以在本机应用中显示 web 内容。 使用 WebView2 可以在本机应用的不同部分嵌入 Web 代码&…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
