搜索(剪枝)
定义:
剪枝,就是减少搜索树的规模、尽早排除搜索树中不必要分支的一种手段。
在深度优先搜索中,有以下几类常见的剪枝方法:
- 优化搜索顺序
- 排除等效冗余
- 可行性剪枝
- 最优性剪枝
- 记忆化剪枝
例题1:AcWing 167.木棒
题目:
https://www.acwing.com/problem/content/169/
将一组等长的木棒随机砍断,得到若干小木棍,计算初始木棒的最小长度
思路:
首先从小到达枚举原木棒长度len,最小的是最大小木棍长度,木棍总和sum满足sum%len==0,根数就是sum/len。如果直接这样暴搜的话会时间超限,所以需要剪枝优化。
1.优化搜索顺序:把木棍长度从大到小排序,优先尝试较长木棍。
2.排除等效冗余:
(1) 限制先后加入一根原始木棒的木棍长度是递减的。因为先拼x再拼y和先拼y再拼x是等效的。
(2) 对于当前原始木棒,记录最近一次尝试拼接木棒的长度。如果搜索失败直接返回false
(3) 如果当前原始木棒中尝试拼入的第一根木棍的递归分支就返回失败,那直接判定失败
(4) 如果在当前原始木棒中拼入一根木棍后,木棒恰好被拼接完整,并且接下来拼接剩余木棒的递归分支返回失败,直接返回失败。
AC代码:
#include<bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;
int a[70],v[70],n,len,cnt;bool dfs(int stick, int cab, int last)
{if(stick>cnt)return true;if(cab==len) return dfs(stick+1,0,1);int falg=0;//剪枝(2) for(int i=last;i<=n;i++){if(!v[i] && cab+a[i]<=len && falg!=a[i]){v[i]=1;if(dfs(stick,cab+a[i],i+1))return true;falg=a[i];v[i]=0;//还原现场if(cab==0 || cab+a[i]==len)//剪枝(3)(4) return false; }}return false;//所有分支都尝试过,搜索失败
}signed main()
{IOSwhile(cin>>n && n){int sum=0, val=0;for(int i=1; i<=n; i++){cin>>a[i];sum+=a[i];val=max(val,a[i]);}sort(a+1,a+n+1);reverse(a+1,a+n+1);for(len=val;len<=sum;len++){if(sum%len) continue;cnt=sum/len;//原始木棒长度为len,共cnt根 memset(v,0,sizeof(v));if(dfs(1,0,1)) break;}cout<<len<<'\n';}return 0;
}
例题2:AcWing 168.生日蛋糕
题目:
https://www.acwing.com/problem/content/170/
一个生日蛋糕,每层都是一个圆柱体,给出体积和层数,找出最小表面积
思路:
从下往上搜索,枚举每层的半径和高度作为分支。整个蛋糕的上表面面积之和等于最底层的圆面积,可以在第m层直接累加到s中,这样在第m-1层搜索中,值需要计算侧面积。
剪枝:
1.在第u层,只需枚举范围内的半径和高度即可
首先,r属于[u,min(sqrt(n-v),r[u+1]-1)];h属于[u,min(sqrt(n-v)/r*r,h[u+1]-1)].
2.在确定范围中,使用倒序枚举。
3.预处理出从上往下前i层的最小体积和侧面积。当1~i层的半径分别取1,2,3……i,高度也分别取1,2,3……i,有最小体积和侧面积。如果当前体积v加上前几层的最小体积大于n,剪枝。
4.如果当前表面积s加上前几层的最小侧面积大于已经搜到的答案,剪枝。
5.比较难敲,看图片。图片中的dep等价于上面的u。
AC代码:
#include<bits/stdc++.h>
#define int long long
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
using namespace std;const int N=25,INT=1e9;
int n,m,r[N],h[N],a[N],b[N],ans=INT;void dfs(int u,int v,int s)
{if(v+a[u]>n) return;if(s+b[u]>=ans) return;if(s+2*(n-v)/r[u+1]>=ans) return;if(!u){if(v==n)ans=s;return;}for(int r1=min(r[u+1]-1,(int)sqrt(n-v));r1>=u;r1--)for(int h1=min(h[u+1]-1,(n-v)/r1/r1);h1>=u;h1--){int t=0;if(u==m)t=r1*r1;r[u]=r1,h[u]=h1;dfs(u-1,v+r1*r1*h1,s+2*r1*h1+t);}
}signed main()
{IOScin>>n>>m;for(int i=1;i<=m;i++){a[i]=a[i-1]+i*i*i;b[i]=b[i-1]+2*i*i;}r[m+1]=h[m+1]=INT;dfs(m,0,0);if(ans==INT) ans=0;cout<<ans<<'\n';return 0;
}
相关文章:

搜索(剪枝)
定义: 剪枝,就是减少搜索树的规模、尽早排除搜索树中不必要分支的一种手段。 在深度优先搜索中,有以下几类常见的剪枝方法: 优化搜索顺序排除等效冗余可行性剪枝最优性剪枝记忆化剪枝 例题1:AcWing 167.木棒 题目:…...
python基础知识点
最近系统温习了一遍python基础语法,把自己不熟知的知识点罗列一遍,便于查阅~~ python教程 Python 基础教程 | 菜鸟教程 1、python标识符 以单下划线开头 _foo 的代表不能直接访问的类属性,需通过类提供的接口进行访问,不能用 f…...
)
Android SurfaceFlinger——GraphicBuffer获取内存信息(三十一)
上一篇文章介绍了 GraphicBuffer 初始化的 initWithSize() 函数中的申请内存流程,这里我们看一下另一个比较重要的函数,GraphicBufferMapper. getTransportSize 获取内存信息。该函数通常在需要了解缓冲区的实际内存占用情况时调用,例如在调试内存使用情况或优化性能时。 一…...

基于 SASL/SCRAM 让 Kafka 实现动态授权认证
一、说明 在大数据处理和分析中 Apache Kafka 已经成为了一个核心组件。然而在生产环境中部署 Kafka 时,安全性是一个必须要考虑的重要因素。SASL(简单认证与安全层)和 SCRAM(基于密码的认证机制的盐化挑战响应认证机制ÿ…...
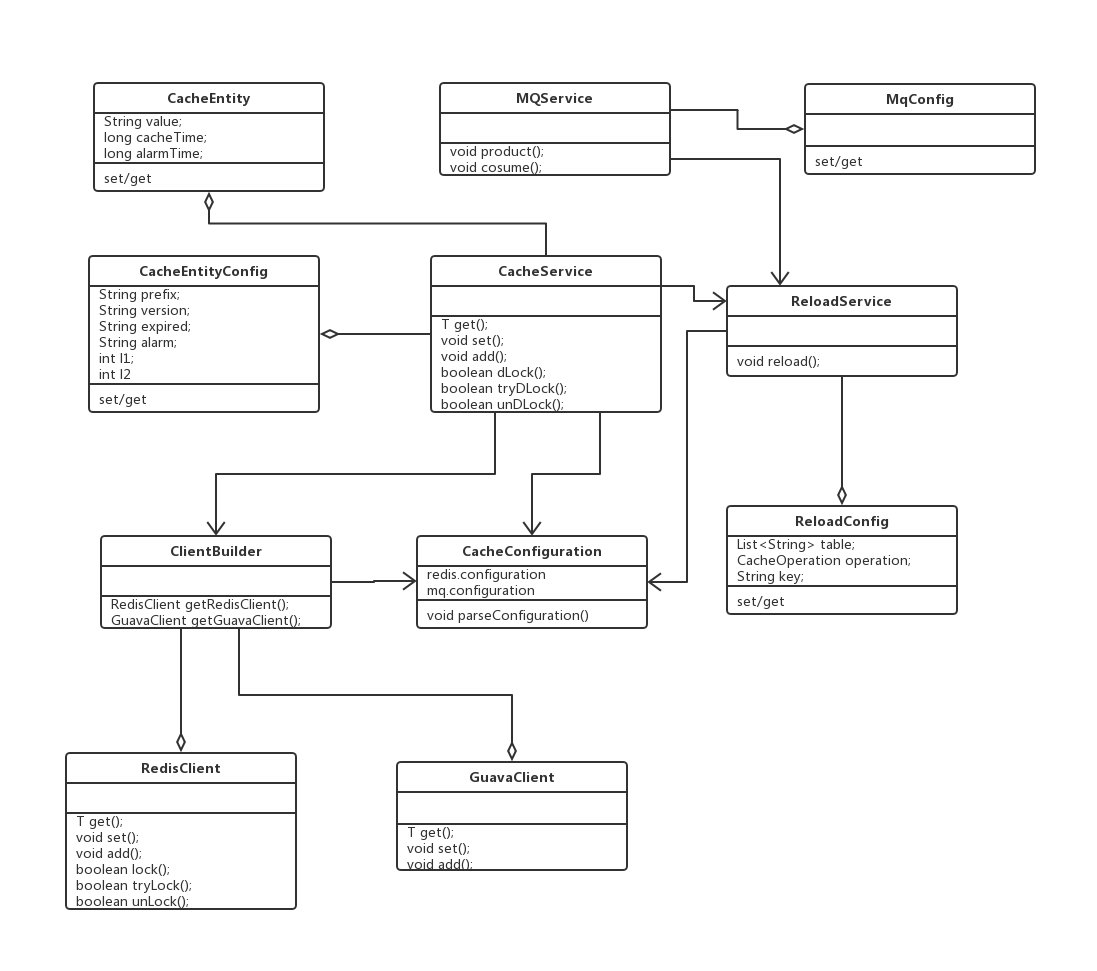
通用多级缓件组件
背景 业界第三方缓存框架一般为redis,本地缓地ehcache或guava,一般通过spring提供的restTemplate操作缓存 然而这样会存在以下问题: 与缓存中间件强耦合需手动整合多级缓存不支持注解数据更新时无法自动刷新缓存存在缓存穿透、缓存击穿、缓…...

MindIE Service服务化集成部署通义千问Qwen模型
一、昇腾开发者平台申请镜像 登录Ascend官网昇腾社区-官网丨昇腾万里 让智能无所不及 二、登录并下载mindie镜像 #登录docker login -u XXX#密码XXX#下载镜像docker pull XXX 三、下载Qwen的镜像 使用wget命令下载Qwen1.5-0.5B-Chat镜像,放在/mnt/Qwen/Qwen1.5-…...
过长问题定位)
chrome 接口请求等待时间(installed 已停止)过长问题定位
参考: 解决实际项目中stalled时间过久的问题 背景: 测试反馈系统开 6 个标签页后, 反应变的很慢 定位: 看接口请求瀑布流, 已停止时间很长, 后端返回速度很快, 确定是前端的问题 推测是并发请求窗口数量的问题, 屏蔽部分一直 pending 的接口, 发现速度正常了, 搜到上面的参…...

HDialog特殊动画效果
基于HDialog的特殊动画效果实现 业务场景 在开发过程中直接使用HDialog所展现的效果很快,同时不能够与用户所点击位置进行交互,会造成用户的体验观感不够好。因此需要实现一种能够从用户点击按钮位置以可变动画效果所展现的Dialog效果。 工作原理及实…...
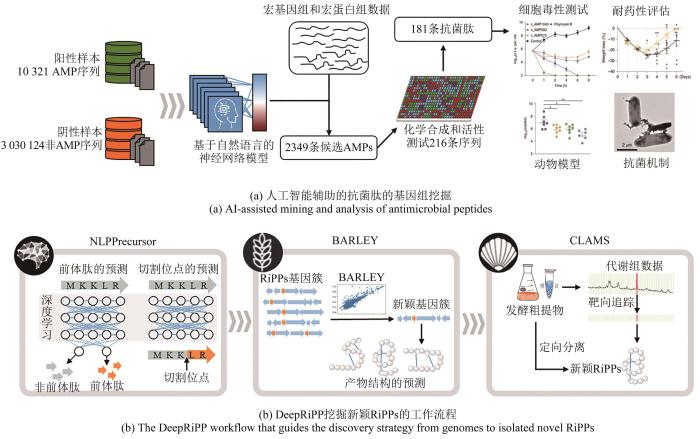
基因组挖掘指导天然药物分子的发现-文献精读34
基因组挖掘指导天然药物分子的发现 摘要 天然产物是临床药物的主要来源,也是新药研发过程中先导化合物结构设计和优化的灵感源泉。但传统策略天然药源分子的发现却遭遇了瓶颈,新颖天然产物的数量逐渐无法满足现代药物开发的需求和应对全球多药耐药的威胁…...

hcip学习 DHCP中继
DHCP 中继 在可能收到 DHCP Discover 报文的接口配置 DHCP 中继, 指明 DHCP 服务器的地址,然后将 DHCP 发现报文以单播的形式送到 DHCP 服务器上 DHCP 中继报文的源地址和目标地址怎么确定 1、源地址:收到 Discover 报文的接口地址 2、目…...

[Mysql-函数、索引]
目录 函数: 日期函数 字符串函数 数学函数 聚合函数 索引: 索引分类 慢查询 创建索引 函数: MySQL函数,是一种控制流程函数,属于数据库用语言。 MySQL常见的函数有: 数学函数 用作常规的数学运…...

org.eclipse.jgit 简单总结
org.eclipse.jgit 是一个用于处理 Git 版本控制系统的纯 Java 库。它允许你读取和写入 Git 仓库,执行如克隆、拉取、推送、提交等操作。下面我将通过几个例子来展示如何使用 org.eclipse.jgit 进行一些常见的 Git 操作。 1. 克隆仓库 克隆一个远程 Git 仓库到本地目…...

Fork软件笔记:一键拉取仓库所有模块
Fork是一个好用的git工具,只是没有中文而已(不过不用翻译也能看使用)。 工具下载地址:https://fork.dev/ 界面展示: 当项目中仓库模块比较多时,可以看到每个模块都是一个分页,每一个都要手动切换…...

常见的锂电保护芯片 单节锂电保护/双节锂电保护芯片
目前外出贸易的要求不断增多,出口的产品基本上都需要带上锂电保护芯片 以下是常见的单节锂电保护芯片的选型 包括了市面上大部分的可用型号。 锂电保护芯片的脚位上面基本都是通用,可以直接替代 双节的锂电保护使用情况较少,需要外置MOS管调节…...
)
初识Java(六)
一、String类 1、类中有操作字符串的方法 查找:找到某个字符是字符串内的第几个:charAt;找到某个字符在字符串内第一次出现的下标:index 替换:替换所有:replaceAll;替换首个:repla…...

Spring-原理篇-DispatcherServlet 初始化 怎么和IOC进行了打通?
委托模式的体现,在初始化醒目的时候Spring MVC为我们提供了一个DispatcherServlet,映射了所有的路径,所有的请求都会先到达这里然后被转发到具体的Controller 进行处理,此文来探索一下,DispatcherServlet 初始化的时候…...

关于swift- OC混编使用Pod遇到的2个错误
错误1 Cannot find interface declaration for UITableViewCell, superclass of "DEFUITalbleViewCell" Cannot find interface declaration for UIView, superclass of "DefUIView" Cannot find interface declaration for 系统类, superclass of "自…...

Golang | Leetcode Golang题解之第290题单词规律
题目: 题解: func wordPattern(pattern string, s string) bool {word2ch : map[string]byte{}ch2word : map[byte]string{}words : strings.Split(s, " ")if len(pattern) ! len(words) {return false}for i, word : range words {ch : patt…...

【Django5】模型定义与使用
系列文章目录 第一章 Django使用的基础知识 第二章 setting.py文件的配置 第三章 路由的定义与使用 第四章 视图的定义与使用 第五章 二进制文件下载响应 第六章 Http请求&HttpRequest请求类 第七章 会话管理(Cookies&Session) 第八章 文件上传…...

HTML--JavaScript操作DOM对象
目录 本章目标 一.DOM对象概念 编辑 二.节点访问方法 常用方法: 层次关系访问节点 三.节点信息 四.节点的操作方法 操作节点的属性 创建节点 删除替换节点 五.节点操作样式 style属性 class-name属性 六.获取元素位置 总结 本章目标 了解DOM的分类和节…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

【实施指南】Android客户端HTTPS双向认证实施指南
🔐 一、所需准备材料 证书文件(6类核心文件) 类型 格式 作用 Android端要求 CA根证书 .crt/.pem 验证服务器/客户端证书合法性 需预置到Android信任库 服务器证书 .crt 服务器身份证明 客户端需持有以验证服务器 客户端证书 .crt 客户端身份…...
