机器学习 | 回归算法原理——随机梯度下降法
Hi,大家好,我是半亩花海。接着上次的多重回归继续更新《白话机器学习的数学》这本书的学习笔记,在此分享随机梯度下降法这一回归算法原理。本章的回归算法原理还是基于《基于广告费预测点击量》项目,欢迎大家交流学习!
目录
一、随机梯度下降法概述
二、案例分析
1. 设置问题
2. 定义模型
3. 随机梯度下降法(拓展)
一、随机梯度下降法概述
随机梯度下降法是一种优化算法,用于最小化目标函数,即减少模型预测和实际结果之间的差距。它是梯度下降算法的一种变体,其核心原理是在每次迭代搜索中,算法随机选择一个样本或数据点(或一小批样本),计算该样本的梯度,然后用这个梯度更新模型参数。
随机梯度下降算法(Stochastic Gradient Descent,SGD)和批量梯度下降算法(Batch Gradient Descent,BGD)的区别在于:随机梯度算法每次只使用少数几个样本点或数据集(每次不重复)的梯度的平均值就更新一次模型;而批量梯度下降算法需要使用所有样本点或数据集的梯度的平均值更新模型。、
举一个经典而形象的例子:假设你现在在山上,为了以最快的速度下山,且视线良好,你可以看清自己的位置以及所处位置的坡度,那么沿着坡向下走,最终你会走到山底。但是如果你被蒙上双眼,那么你则只能凭借脚踩石头的感觉判断当前位置的坡度,精确性就大大下降,有时候你认为的坡,实际上可能并不是坡,走一段时间后发现没有下山,或者曲曲折折走了好多路才能下山。类似的,批量梯度下降法就好比正常下山,而随机梯度下降法就好比蒙着眼睛下山。
因此,随机梯度下降算法的效率明显提高,目前已经得到了广泛应用。
例子来源于:《详解随机梯度下降法(Stochastic Gradient Descent,SGD)_随机梯度下降公式-CSDN博客》
二、案例分析
1. 设置问题
在介绍随机梯度下降法之前,我们先得知道之前研究过最速下降法,它除了计算花时间以外,还有一个缺点那就是容易陷入局部最优解。
在讲解回归时,我们使用的是平方误差目标函数。这个函数形式简单,所以用最速下降法也没有问题。现在我们来考虑稍微复杂一点的,比如这种形状的函数:

用最速下降法来找函数的最小值时,必须先要决定从哪个 开始找起。之前我用
说明的时候是从
或者
开始的,那是为了讲解而随便选的作为初始值。选用随机数作为初始值的情况比较多。不过这样每次初始值都会变,进而导致陷入局部最优解的问题。
假设这张图中标记的位置就是初始值:

倘若从这个点开始找,似乎可以求出最小值。但是如果我们换一个初始点,如下所示,那么可能没计算完就会停止,便陷入了局部最优解。

这个算法虽然简单,但是容易发生各种问题,但最速下降法也不会白学,随机梯度下降法就是以最速下降法为基础的。
2. 定义模型
由 《机器学习 | 回归算法原理——最速下降法(梯度下降法)-CSDN博客》可知,最速下降法的参数更新表达式为:
这个表达式使用了所有训练数据的误差,而在随机梯度下降法中会随机选择一个训练数据,并使用它来更新参数。下面这个表达式中的 就是被随机选中的数据索引。
最速下降法更新 1 次参数的时间,随机梯度下降法可以更新 次。 此外,随机梯度下降法由于训练数据是随机选择的,更新参数时使用的又是选择数据时的梯度,所以不容易陷入目标函数的局部 最优解,在实际运用上的确会收敛。
3. 随机梯度下降法(拓展)
我们前面提到了随机选择 1 个训练数据的做法,此外还有随机选择 个训练数据来更新参数的做法。设随机选择
个训练数据的索引的集合为
,则更新参数如下:
现在假设训练数据有 100 个,那么在 时,创建一个有 10 个随机数的索引的集合,例如
,然后重复更新参数,这种做法被称为小批量(mini-batch)梯度下降法。 这像是介于最速下降法和随机梯度下降法之间的方法。
ps:不论是随机梯度下降法还是小批量梯度下降法,我们都必须考虑学习率 ,将
设置为合适的值是尤为重要。
相关文章:
机器学习 | 回归算法原理——随机梯度下降法
Hi,大家好,我是半亩花海。接着上次的多重回归继续更新《白话机器学习的数学》这本书的学习笔记,在此分享随机梯度下降法这一回归算法原理。本章的回归算法原理还是基于《基于广告费预测点击量》项目,欢迎大家交流学习!…...

LeetCode 面试经典 150 题 | 位运算
目录 1 什么是位运算?2 67. 二进制求和3 136. 只出现一次的数字4 137. 只出现一次的数字 II5 201. 数字范围按位与 1 什么是位运算? ✒️ 源自:位运算 - 菜鸟教程 在现代计算机中,所有数据都以二进制形式存储,…...

postMessage 收到消息类型 “webpackWarnings“
场景描述: 当A系统中的parent页面使用iframe内嵌C系统的child页面,并且在parent页面中通过postMessageg给child页面发送消息时,如果C系统中使用了webpack,则webpack也会给child页面发送消息 ,消息类型为webpackWarnings。那么如何…...

计算机基础(day1)
1.什么是内存泄漏?什么是内存溢出?二者有什么区别? 2.了解的操作系统有哪些? Windows,Unix,Linux,Mac 3. 什么是局域网,广域网? 4.10M 兆宽带是什么意思?理论…...

cesium添加流动线
1:新建Spriteline1MaterialProperty.js文件 import * as Cesium from cesium;export function Spriteline1MaterialProperty(duration, image) {this._definitionChanged new Cesium.Event();this.duration duration;this.image image;this._time performance.…...

使用java自带的队列进行存取数据ArrayBlockingQueue 多线程读取ExecutorService
场景: 防止接收数据时处理不过来导致阻塞,使用ArrayBlockingQueue队列存储数据后,以多线程的方式处理数据 保证系统性能。 package com.yl.demo.main4;import java.text.SimpleDateFormat; import java.util.Date; import java.util.concurr…...

【音视频之SDL2】Windows配置SDL2项目模板
文章目录 前言 SDL2 简介核心功能 Windows配置SDL2项目模板下载SDL2编译好的文件VS配置SDL2 测试代码效果展示 总结 前言 在开发跨平台的音视频应用程序时,SDL2(Simple DirectMedia Layer 2)是一个备受欢迎的选择。SDL2 是一个开源库&#x…...

JavaScript 里的深拷贝和浅拷贝
JavaScript 里的深拷贝和浅拷贝 JS中数据类型分为基本数据类型和引用数据类型。 基本类型值指的是那些保存在栈内存中的简单数据段。包含Number,String,Boolean,Null,Undefined ,Symbol。 引用类型值指的是那些保存…...

Oracle基础-集合
集合:两个结果集的字段个数和字段类型必须相同,才能使用集合操作。 --UNION 并集 重复行会去重 (SELECT A,B FROM DUAL UNION SELECT C,D FROM DUAL) UNION (SELECT A,B FROM DUAL UNION SELECT E,F FROM DUAL ); --UNION ALL 全集 包含所有记录 不去重…...

《浅谈如何培养树立正确的人工智能伦理观念》
目录 摘要: 一、引言 二、《机械公敌》的情节与主题概述 三、人工智能伦理与法律问题分析 1.伦理挑战 2.法律问题 四、培养正确的人工智能伦理观念的重要性 五、培养正确的人工智能伦理观念的途径与方法 1.加强教育与宣传 2.制定明确的伦理准则和规范 3.…...
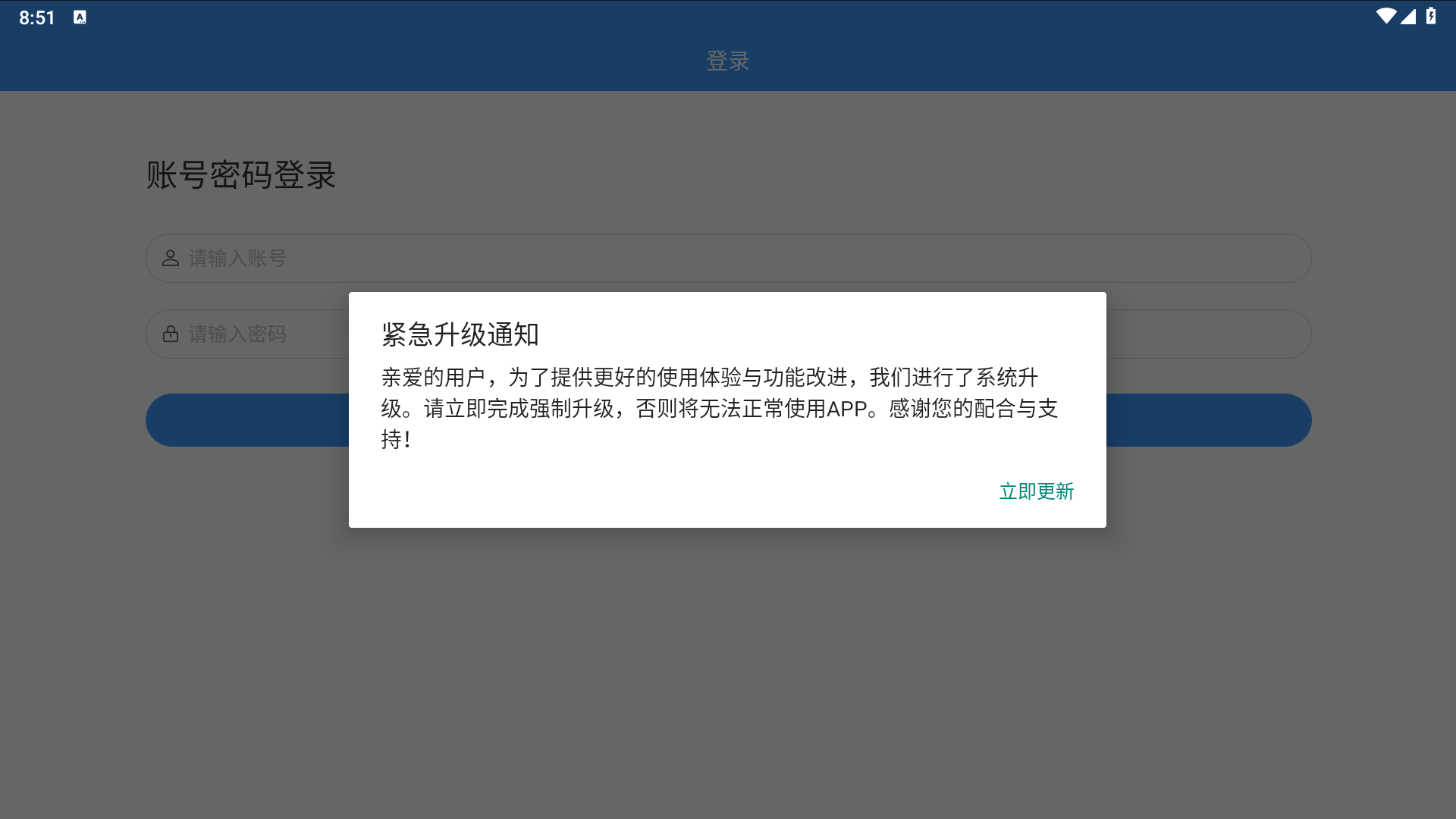
uniapp实现局域网(内网)中APP自动检测版本,弹窗提醒升级
uniapp实现局域网(内网)中APP自动检测版本,弹窗提醒升级 在开发MES系统的过程中,涉及到了平板端APP的开发,既然是移动端的应用,那么肯定需要APP版本的自动更新功能。 查阅相关资料后,在uniapp的…...
)
【Golang 面试 - 进阶题】每日 3 题(六)
✍个人博客:Pandaconda-CSDN博客 📣专栏地址:http://t.csdnimg.cn/UWz06 📚专栏简介:在这个专栏中,我将会分享 Golang 面试中常见的面试题给大家~ ❤️如果有收获的话,欢迎点赞👍收藏…...
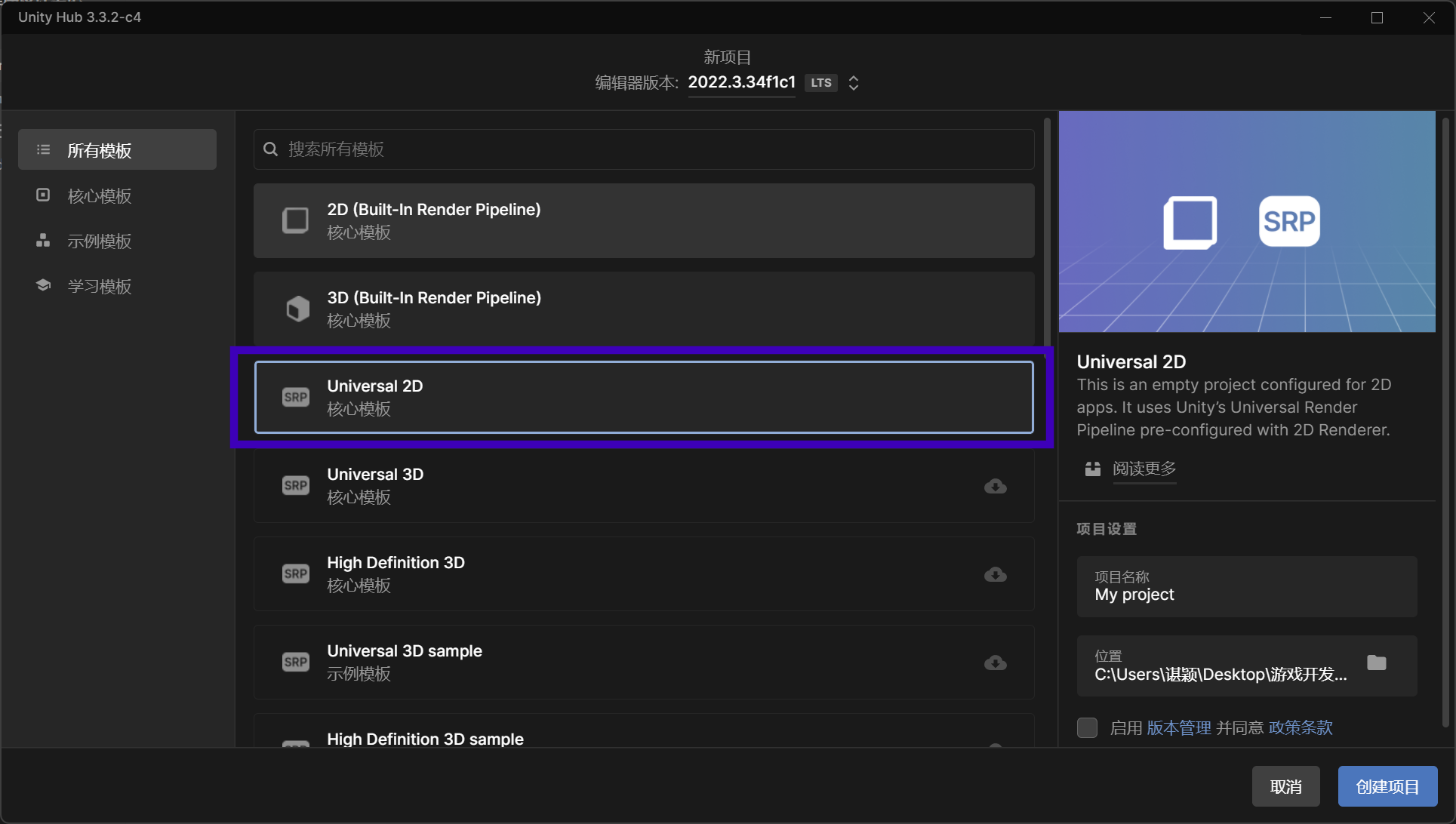
Unity横板动作游戏 -项目准备
项目准备 这是一篇 Unity 2022 最新稳定版本的教程同步笔记,本文将会讲解一些开始学习必须的条件。 安装环境 首先是安装 UnityHub,然后在 UnityHub 中安装 Unity 的版本(2022)。 只需要安装 开发者工具 和文档即可,导出到其他平台的工具等…...

基于Gunicorn + Flask + Docker的高并发部署策略
标题:基于Gunicorn Flask Docker的高并发部署策略 引言 随着互联网用户数量的增长,网站和应用程序需要能够处理越来越多的并发请求。Gunicorn 是一个 Python WSGI HTTP 服务器,Flask 是一个轻量级的 Web 应用框架,Docker 是一…...

jdk版本管理利器-sdkman
1.什么是sdkman? sdkman是一个轻量级、支持多平台的开源开发工具管理器,可以通过它安装任意主流发行版本(例如OpenJDK、Kona、GraalVM等等)的任意版本的JDK。通过下面的命令可以轻易安装sdkman: 2.安装 curl -s "https://…...

Kafka知识总结(事务+数据存储+请求模型+常见场景)
文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 文章收录在网站:http://hardyfish.top/ 事务 事务Producer保证消息写入分区的原子性,即这批消…...

C#中重写tospring方法
在C#中,重写ToString方法允许你自定义对象的字符串表示形式。当你想要打印对象或者在调试时查看对象的状态时,重写ToString方法非常有用。 默认情况下,ToString方法返回对象的类型名称。通过重写这个方法,你可以返回一个更有意义…...

【机器学习基础】机器学习的数学基础
【作者主页】Francek Chen 【专栏介绍】 ⌈ ⌈ ⌈Python机器学习 ⌋ ⌋ ⌋ 机器学习是一门人工智能的分支学科,通过算法和模型让计算机从数据中学习,进行模型训练和优化,做出预测、分类和决策支持。Python成为机器学习的首选语言,…...

fastapi之零
FastAPI 详细介绍 FastAPI 是一个现代、快速(高性能)的 web 框架,用于构建 API。它基于标准的 Python 类型提示,使用 Starlette 作为 web 框架,Pydantic 进行数据验证和解析。以下是对 FastAPI 的详细介绍,…...

SpringBoot整合PowerJob 实现远程任务
PowerJob介绍 PowerJob 是全新一代分布式任务调度和计算框架,提供了可视化界面,可通过单机、远程等形式调用任务并提供了运行监控和日志查看的功能模块,是当前比较流行的分布式定时任务框架之一; PowerJob 官网文档地址 环境搭建…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...
