[补题记录]Leetcode 15. 三数之和
传送门:三数之和
思路
为了去重,需要先排序。
排序之后,显然每一个 n u m s [ i ] nums[i] nums[i] 就可以作为三数之中的第一个数。
因此,对于每一个 i i i,第二、三个数只能在 [ i + 1 , n ] [i + 1, n] [i+1,n] 之间取得。
这时候如果使用 map 去维护每个 nums 对应的所有下标(例如:std::map <int, std::vector<int>> mp;),实际上还是会超时。因为即使确定了第一、二个数,当查找第三个数时,哪怕用二分,都还要再乘上一个 l o g n logn logn 的复杂度。
但这也同时提醒我们,如果确定了第二、三个数,那就可以判断出 n u m s [ 2 ] + n u m s [ 3 ] nums[2] + nums[3] nums[2]+nums[3] 是大于还是小于 − n u m s [ 1 ] - nums[1] −nums[1],这就意味着我们可以通过移动 2、3 指针的方式,来找到 n u m s [ 2 ] + n u m s [ 3 ] = − n u m s [ 1 ] nums[2] + nums[3] = - nums[1] nums[2]+nums[3]=−nums[1] 的情况。
因此这道题可以用双指针的方式来做,还是有点难想的。
还需要额外注意 [… , a , a , …] 和 [ … , a , b , b , … ] 这两种特殊情况。
代码
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {std::sort(nums.begin(), nums.end());std::vector<std::vector<int>> result;for (int i = 0; i < nums.size(); ++ i) {int sum = -nums[i];// 防止 a aif (i >= 1 && nums[i] == nums[i - 1]) continue;int r = nums.size() - 1; for (int l = i + 1; l < nums.size(); ++ l) {// 防止 a b bif (l > i + 1 && nums[l] == nums[l - 1]) continue;while (r > l && nums[l] + nums[r] > sum) r--;if (l == r) break;if (nums[l] + nums[r] == sum) {result.push_back({nums[i], nums[l], nums[r]});}}} return result;}
};
相关文章:

[补题记录]Leetcode 15. 三数之和
传送门:三数之和 思路 为了去重,需要先排序。 排序之后,显然每一个 n u m s [ i ] nums[i] nums[i] 就可以作为三数之中的第一个数。 因此,对于每一个 i i i,第二、三个数只能在 [ i 1 , n ] [i 1, n] [i1,n]…...

什么是sql注入攻击,如何预防介绍一下mysql中的常见数据类型
什么是sql注入攻击,如何预防 sql注入攻击指的是应用程序对用户输入数据的合法性没有判断或者过滤不严格,在sql语句中插入任意的恶意语句进行非法操作。 预防方式1:使用预编译语句比如PrepareStatement,用户输入的所有数据都以参数…...

史上最全的Seata教学并且连接springcloudAlibaba进行使用
来都来了点个赞收藏一下在走呗~~🌹🌹玫瑰 一、Seata是什么 Seata(Simple Extensible Autonomous Transaction Architecture,简单可扩展自治事务框架)是一种分布式事务解决方案,旨在解决分布式系统中的事务…...
InternLM Git 基础知识
提交一份自我介绍。 创建并提交一个项目。...

【Unity模型】古代亚洲建筑
在Unity Asset Store上,一款名为"Ancient Asian Buildings Pack"(古代亚洲建筑包)的3D模型资源包,为广大开发者和设计师提供了一个将古代亚洲建筑风格融入Unity项目的机会。本文将详细介绍这款资源包的特点、使用方式以…...

木马后门实验
实验拓扑 实验步骤 防火墙 配置防火墙—充当边界NAT路由器 边界防火墙实现内部 DHCP 分配和边界NAT需求,其配置如下 登录网页 编辑接口 配置e0/0 配置e0/1 编辑策略 测试:内部主机能获得IP,且能与外部kali通信 kali 接下来开启 kali 虚…...

【React】useState:状态更新规则详解
文章目录 一、基本用法二、直接修改状态 vs 使用 setState 更新状态三、对象状态的更新四、深层次对象的更新五、函数式更新六、优化性能的建议 在 React 中,useState 是一个非常重要的 Hook,用于在函数组件中添加状态管理功能。正确理解和使用 useState…...

C#中的异步编程:Task、Await 和 Async
public async void DoSth() {await Task.Run(() > {//...DoSth...}); } ①函数的返回类型前加上: async ②函数内加上: await Task.Run(() > { }); ③在上面{ ... } 内添加要处理的程序代码, 这样运行到 DoSth() 函数就…...
SSRF-labs-master靶场
目录 file_get_content.php sql_connect.php download.php dns-spoofing.php dns_rebinding.php 访问链接 http://127.0.0.1/SSRF/# file_get_content.php 在编程语言中,有一些函数可以获取本地保存文件的内容。这些功能可能能够从远程URL以及本地文件 如果没…...

HBuilder X中配置vue-cli项目和UI库
目录 一.前端项目结构 二.在HBuilder X中搭建vue-cli项目 1. 安装node.js前端环境 2. HBuilder X创建一个vue-cli项目 3. vue-cli项目结构 4. 如何运行前端项目 5. 创建组件 6. 组件路由(页面跳转) 6.1 创建router目录 6.2 使用路由 6.3 在main.js中配置路由 6.4 路…...
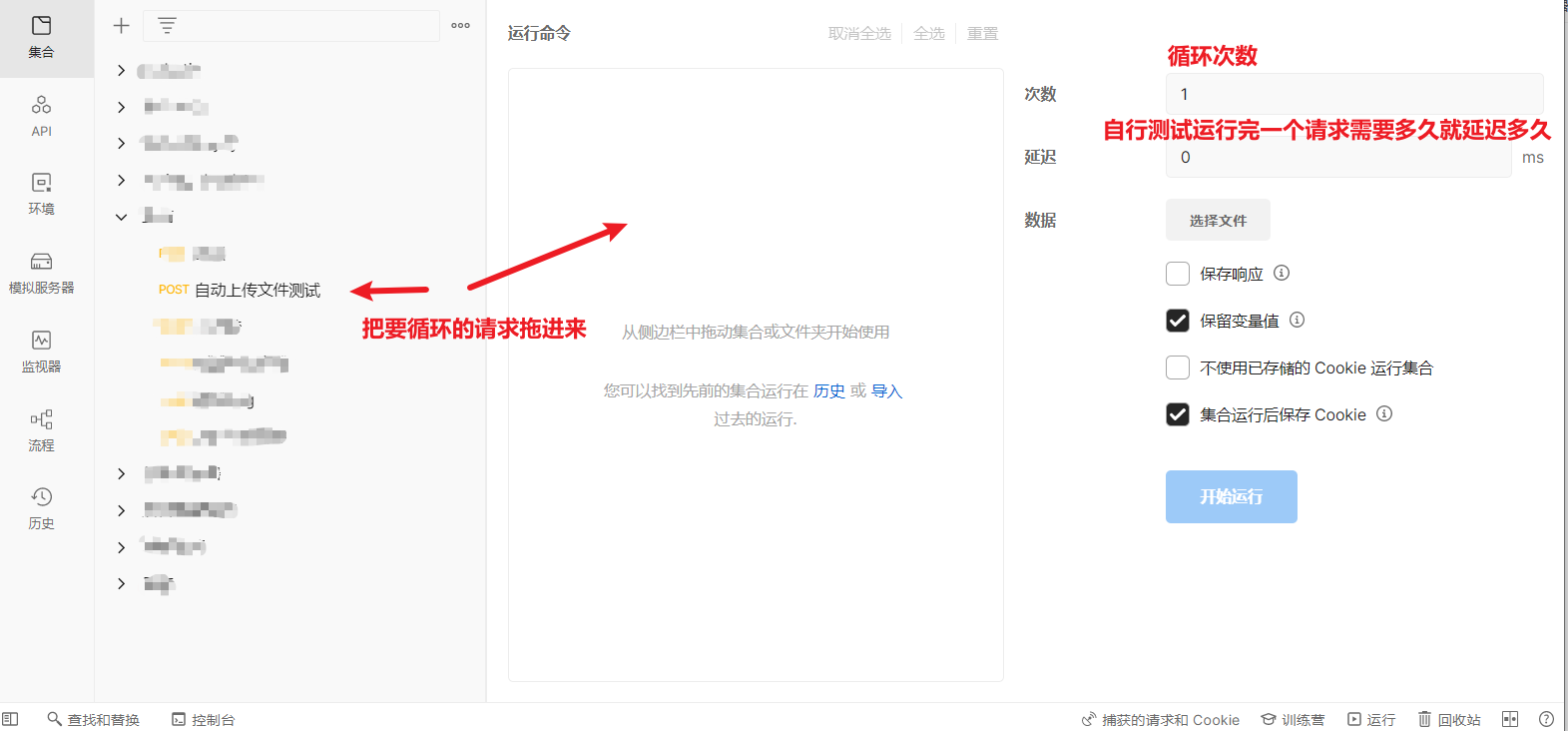
如何用PostMan按照规律进行循环访问接口
①设置动态变量 步骤一: 设置环境变量 1. 创建环境变量集合 在 Postman 左上角选择 "环境",然后点击 "添加" 来创建一个新的环境变量集合。给它起一个名称,比如 "uploadDemo". 2. 添加初始变量 在新创建的环境变量集…...
稳态准直太阳光模拟器仪器光伏电池组件IV测试
太阳能模拟器电池IV测试仪、单体测试仪,配备匹配标准的AAA Class稳态太阳能模拟器及相关测试附件,可对太阳能电池片的IV性能进行测量、分级分选等; 介绍 AAA class太阳光模拟器整合完整的IV测量系统,针对各种太阳能电池的性能&a…...
-代理Set和Map及ref原理)
vue3 reactive原理(二)-代理Set和Map及ref原理
Set和Map类型的数据也属于异质对象,它们有特定的属性和方法用来操作自身。因此创建代理时,针对特殊的方法需要特殊的对待。 Vue 的ref 是基于reactive函数实现的,它在其基础上,增加了基本类型的响应性、解决reactive在解构时丢失…...

Python自然语言处理库之NLTK与spaCy使用详解
概要 自然语言处理(NLP)是人工智能和数据科学领域的重要分支,致力于让计算机理解、解释和生成人类语言。在Python中,NLTK(Natural Language Toolkit)和spaCy是两个广泛使用的NLP库。本文将详细介绍NLTK和spaCy的特点、功能及其使用方法,并通过具体示例展示如何使用这两…...

Hive-内部表和外部表
区别 内部表实例 准备数据 查看数据 删除数据 外部表实例 准备数据 查看数据 删除数据 区别 内部表:管理元数据(记录数据的文件和目录的信息)和数据。当删除内部表时,会删除数据和表的元数据,所以当多个表关…...
)
Java并发编程(三)
Java并发编程 1、什么是 Executors 框架 Executors框架是一个根据一组执行策略调用,调度,执行和控制的异步任务的框架。 无限制的创建线程会引起应用程序内存溢出。所以创建一个线程池是个更好的的解决方案,因为可以限制线程的数量并且可以…...

Flink Doirs Connector 常见问题:Doris目前不支持流读
常见问题 Doris Source 在数据读取完成后,流为什么就结束了? 目前 Doris Source 是有界流,不支持 CDC 方式读取。 问题:对于 Flink Doris DataStream,Flink 想要在 流式读取 Doirs / 实时读 Doris,目前读…...

期末复习资料——计算机系统基础
第一章 1、下列关于机器字长、指令字长和存储字长的说法中,正确的时_②、③_ ①三者在数值上总是相等的。②三者在数值上可能不相等。③存储字长是存放在一个存储单元中的二进制代码位数。④数据字长就是MDR的位数。 机器字长、指令字长和存储字长,三…...
——ReactRouter(上)【已完结】)
一天搞定Recat(5)——ReactRouter(上)【已完结】
Hello!大家好,今天带来的是React前端JS库的学习,课程来自黑马的往期课程,具体连接地址我也没有找到,大家可以广搜巡查一下,但是总体来说,这套课程教学质量非常高,每个知识点都有一个…...

TCP/IP 网络模型详解(二)之输入网址到网页显示的过程
当键入网址后,到网页显示,其间主要发生了以下几个步骤: 一、解析URL 下图是URL各个元素所表示的意义: 右边蓝色部分(文件的路径名)可以省略。当没有该数据时,代表访问根目录下事先设置的默认文…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

海云安高敏捷信创白盒SCAP入选《中国网络安全细分领域产品名录》
近日,嘶吼安全产业研究院发布《中国网络安全细分领域产品名录》,海云安高敏捷信创白盒(SCAP)成功入选软件供应链安全领域产品名录。 在数字化转型加速的今天,网络安全已成为企业生存与发展的核心基石,为了解…...

Git 命令全流程总结
以下是从初始化到版本控制、查看记录、撤回操作的 Git 命令全流程总结,按操作场景分类整理: 一、初始化与基础操作 操作命令初始化仓库git init添加所有文件到暂存区git add .提交到本地仓库git commit -m "提交描述"首次提交需配置身份git c…...

【Redis】Redis从入门到实战:全面指南
Redis从入门到实战:全面指南 一、Redis简介 Redis(Remote Dictionary Server)是一个开源的、基于内存的键值存储系统,它可以用作数据库、缓存和消息代理。由Salvatore Sanfilippo于2009年开发,因其高性能、丰富的数据结构和广泛的语言支持而广受欢迎。 Redis核心特点:…...

【Pandas】pandas DataFrame dropna
Pandas2.2 DataFrame Missing data handling 方法描述DataFrame.fillna([value, method, axis, …])用于填充 DataFrame 中的缺失值(NaN)DataFrame.backfill(*[, axis, inplace, …])用于**使用后向填充(即“下一个有效观测值”)…...

基于微信小程序的作业管理系统源码数据库文档
作业管理系统 摘 要 随着社会的发展,社会的方方面面都在利用信息化时代的优势。互联网的优势和普及使得各种系统的开发成为必需。 本文以实际运用为开发背景,运用软件工程原理和开发方法,它主要是采用java语言技术和微信小程序来完成对系统的…...
