LeetCode每日练习 | 二分查找 | 数组 |Java | 图解算法


🌈个人首页: 神马都会亿点点的毛毛张

📌 你真的刷明白了二分查找吗⁉️记得看毛毛张每个题目中写的【注意细节】⚠️
文章目录
- 0.前言🍁
- 1.[704. 二分查找🍍](https://leetcode.cn/problems/binary-search/)
- 1.1 题目描述🥥
- 1.2 题解🍈
- 1.2.1 二分查找写法1
- 1.2.2 二分查找写法2
- 1.3 注意细节⚠️
- 2.[35. 搜索插入位置🍎](https://leetcode.cn/problems/search-insert-position/)
- 2.1 题目描述🍏
- 2.2 题解🥦
- 2.2.1 暴力求解
- 2.2.2 二分查找写法1
- 2.2.3 二分查找写法2
- 3.[69. x 的平方根 🍊](https://leetcode.cn/problems/sqrtx/)
- 3.1 题目描述🌽
- 3.2 题解🍓
- 3.2.1 使用内置函数
- 3.2.2 暴力解法
- 3.2.3 二分查找法
- 3.2.4 牛顿迭代法
- 3.3 练习:[367. 有效的完全平方数🍒](https://leetcode.cn/problems/valid-perfect-square/)
- 3.3.1 题目描述🍇
- 3.3.2 题解
- 3.3.2.1 使用内置函数
- 3.3.2.2 暴力解法
- 3.3.2.3 二分查找法
- 3.3.2.4 牛顿迭代法
- 3.4 注意细节⚠️
- 4.[34. 在排序数组中查找元素的第一个和最后一个位置🍌](https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/)
- 4.1 题目描述🍍
- 4.2 题解🥭
- 4.2.1 暴力解法
- 4.2.2 二分查找写法1
- 4.2.3 二分查找写法2
- 5.总结🌍
- 参考文献🎁
0.前言🍁
- 📌毛毛张在刷算法题的时候有两个感悟:
- 1️⃣有很多算法题的难点在于对于特殊情况的判断,很多时候我们实现的算法能通过大部分的测试案例,但是对于一些特殊案例不能通过,这可能是因为逻辑本来就错误,那么我们的算法需要重新设计考虑,另一种原因是因为算法对于一些边界问题没有考虑进去,那么我们需要对于算法的一些特殊情况的判断要考虑进去
- 2️⃣很多算法题刷到后面就是数学题,如果能有比较好的数学基础,对于求解一些算法题是有帮助的,但是对于大多数人来说,数学都不是很好,包括毛毛张在内,所以毛毛张在刷算法题的时候很少直接使用数学方法来求解题目,毛毛张在介绍的时候也希望通过简单的逻辑思考而不需要很高深的数学问题来求解算法,这样才能让每个人都学习算法,而不是觉得算法很难,不能接受
- 📌今天毛毛张要分享的代码随想录中的第一个题目:二分查找,这个在查找算法中一个比较简单的算法,并且在
LeetCode也是一道比较简单的题目,但是里面却有很多需要注意的细节
1.704. 二分查找🍍
LeetCode标签:简单
1.1 题目描述🥥
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
1.2 题解🍈
- 二分查找是利用数组的有序性,每轮缩窄一半的查找区间(即排除一半元素),直到找到目标值或查找区间为空时返回的查找算法
- 时间复杂度: 由于每轮可以排除一半元素,因此查找最多循环 l o g 2 N log_2N log2N 次,所以时间复杂度 O ( l o g 2 N ) O(log_2N) O(log2N)
- 在数据量较大时,二分查找的效率大幅高于线性查找 O ( N ) O(N) O(N)
- 我们通过下面算法流程来理解二分查找法的缩窄区间的含义:给定升序数组
nums和目标值target,二分查找流程如下- 第一步:定义查找区间,初始化双指针
min、max分别指向数组首、尾元素,代表查找区间为闭区间[min,max]; - 第二步:循环二分,缩窄查找区间:
- 使用向下取整除法,计算区间 [ m i n , m a x ] [min,max] [min,max]的中点
mid; - 若 n u m s [ m i d ] < t a r g e t nums[mid]<target nums[mid]<target ,根据数组有序性,易得 t a r g e t target target一定不在闭区间 [ m i n , m i d ] [min,mid] [min,mid]中,因此执行 m i n = m i d + 1 min=mid+1 min=mid+1 ,即将查找区间缩窄至 [ m i d + 1 , m a x ] [mid+1,max] [mid+1,max];
- 若 n u m s [ m i d ] > t a r g e t nums[mid]>target nums[mid]>target, 根据数组有序性,易得 t a r g e t target target一定不在闭区间 [ m i d , m a x ] [mid,max] [mid,max]中,因此执行 m a x = m i d − 1 max=mid−1 max=mid−1,即将查找区间缩窄至 [ m i n , m i d − 1 ] [min,mid−1] [min,mid−1];
- 若 n u m s [ m i d ] = t a r g e t nums[mid]=target nums[mid]=target ,说明找到 t a r g e t target target,返回索引 m i d mid mid即可;
- 使用向下取整除法,计算区间 [ m i n , m a x ] [min,max] [min,max]的中点
- 不满足 m i n ≤ m a x min≤max min≤max时跳出循环,此时代表无法在数组中找到目标值
target,因此返回 − 1 -1 −1
- 第一步:定义查找区间,初始化双指针
- 上面的二分查找的流程非常详细,然鹅在具体的代码实现过程中,根据二分查找区间的开闭情况又可以分为两种写法:
- 如果二分查找区间均为闭区间
[min,max],则循环结束判断条件为while(min <= max),对应下面写法1 - 如果二分查找区间均为左闭右开区间
[min,max),则循环结束判断条件为while(min < max),对应下面写法2
- 如果二分查找区间均为闭区间
- 上面的理论分析和分类说明比较枯燥,大家可以看下面的图解和代码实现
1.2.1 二分查找写法1
算法图解:



算法实现:
class Solution {public int search(int[] nums, int target) {// 左边索引int min = 0;// 右边索引int max = nums.length - 1;// 开始二分查找逻辑while (min <= max) {// 中间索引int mid = (max - min) / 2 + min;// 获取中间值,并进行比较if (nums[mid] == target) {return mid;} else if (target > nums[mid]) {min = mid + 1;} else {max = mid - 1;}}return -1;}
}
1.2.2 二分查找写法2
算法图解:
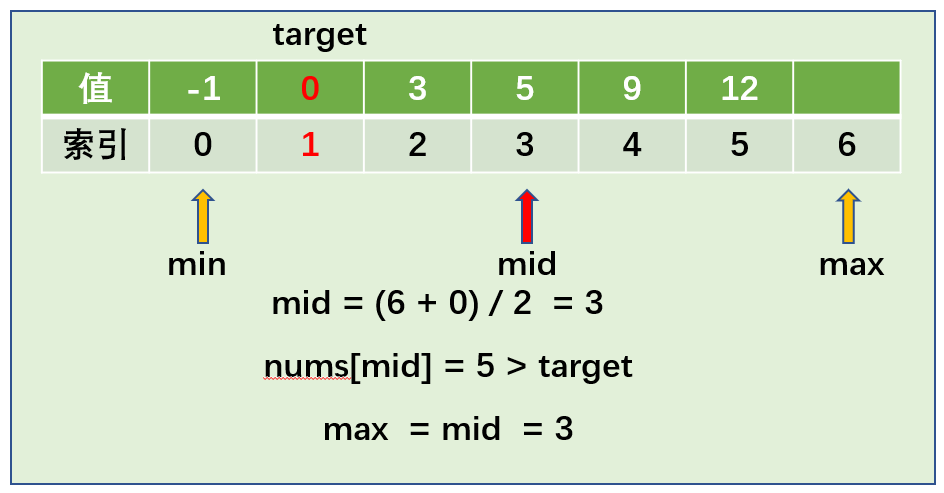
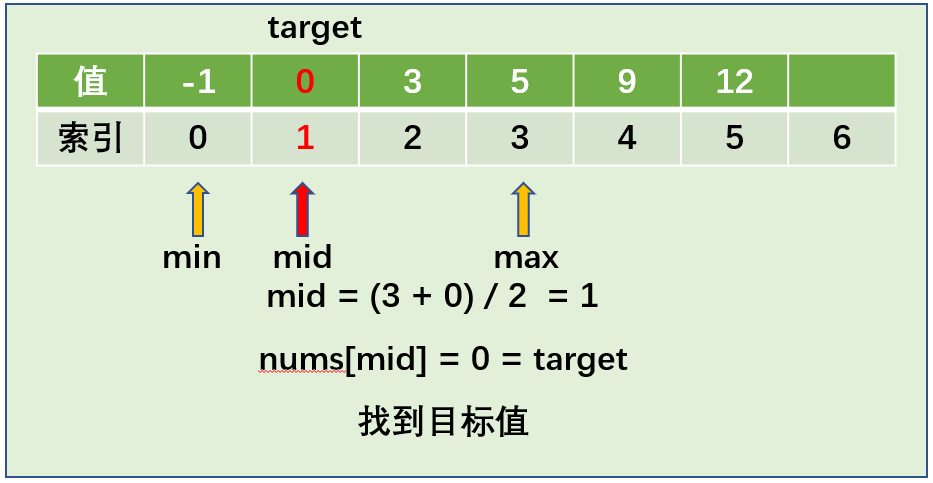
算法实现:
class Solution {public int search(int[] nums, int target) {// 左边索引int min = 0;// 右边索引int max = nums.length;// 开始二分查找逻辑while (min < max) {// 中间索引int mid = (max - min) / 2 + min;// 获取中间值,并进行比较if (nums[mid] == target) {return mid;} else if (target > nums[mid]) {min = mid + 1;} else {max = mid;}}return -1;}
}
1.3 注意细节⚠️
- 这个题目的是二分查找的入门题目,比较简单,但是有两个细节需要注意:
- 细节1: 就是前面说到的根据查找区间的开闭情况不同,结束循环的条件也应该不同
- 细节2: 计算中间索引所用的公式,有以下两种写法
- 写法1:
int mid = (max + min) / 2;,但是可能会导致溢出,如果max和min都是非常大的正数或负数,max + min的值可能会超过int类型的范围。 - 写法2:
int mid = (max - min) / 2 + min;,避免了溢出问题,因为max - min不会超过max或min的范围。 - 代码说明:
max = Integer.MAX_VALUE; min = Integer.MAX_VALUE - 1; int mid = (max - min) / 2 + min; // 结果为 Integer.MAX_VALUE - 1 int mid = (max + min) / 2; // 结果可能导致溢出,变为负数
- 写法1:
- 根据毛毛张在上面的写法中可以看出,对于计算中间值
mid,毛毛张跟倾向于下面的写法,虽然在此题中不会出现溢出的情况,但是在别的题目中就可能会出现,例如下面的相关题目!
2.35. 搜索插入位置🍎
LeetCode标签:简单
2.1 题目描述🍏
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
- 1 < = n u m s . l e n g t h < = 1 0 4 1 <= nums.length <= 10^4 1<=nums.length<=104
- − 1 0 4 < = n u m s [ i ] < = 1 0 4 -10^4 <= nums[i] <= 10^4 −104<=nums[i]<=104
nums为 无重复元素 的 升序 排列数组- − 1 0 4 < = t a r g e t < = 1 0 4 -10^4 <= target <= 10^4 −104<=target<=104
2.2 题解🥦
- 这很明显是一道查找的题目,并且要求时间复杂度为
O(log n)的算法,于是很容易想到采用二分查找。 - 与上面第一道题目的不同之处在于,第一道题目关注的是否找得到,此题还需要关注找不到时插入的位置,因此,我们需要关注退出循环之后的
min和max的值代表什么? 清楚知道这一点是求解本题的关键,同样根据二分查找区间的开闭情况分为两种写法 - 在做题之前我们还需要考虑到这个题目插入的四种情况:
- 目标值在数组所有元素之前
- 目标值等于数组中某一个元素
- 目标值插入数组中的位置
- 目标值在数组所有元素之后

- 这道题目要求算法实现复杂度为 O ( l o g ( N ) ) O(log(N)) O(log(N)),但是也不要忘记了最简单质朴的解法,所以毛毛张在这里首先还是要介绍一下暴力解法
2.2.1 暴力求解
class Solution {public int searchInsert(int[] nums, int target) {//暴力解法int i;for(i = 0;i < nums.length;i++){// 一旦发现大于或者等于target的num[i],那么i就是我们要的结果if(nums[i] >= target) break; }//如果target大于整个数组,那么循环结束后 i = nums.lengthreturn i;}
}
2.2.2 二分查找写法1
class Solution {public int searchInsert(int[] nums, int target) {//二分查找int left = 0;int right = nums.length;while(left < right){// 因为left == right的时候,在[left, right)是无效的空间int mid = (left + right) / 2;if(target == nums[mid]) return mid;// 数组中找到目标值的情况,直接返回下标else if(target > nums[mid]){left = mid + 1;// target 在右区间,在 [mid+1, right)中}else{right = mid;// target 在左区间,在[left, mid)中}}// 分别处理如下四种情况// 目标值在数组所有元素之前 [0,0)// 目标值等于数组中某一个元素 return mid// 目标值插入数组中的位置 [left, right) ,return right 即可// 目标值在数组所有元素之后的情况 [left, right),因为是右开区间,所以 return rightreturn right;}
}
2.2.3 二分查找写法2
class Solution {public int searchInsert(int[] nums, int target) {//二分查找int left = 0;int right = nums.length - 1;// 定义target在左闭右闭的区间里,[left, right]while(left <= right){// 当left==right,区间[left, right]依然有效int mid = (left + right) / 2;if(target == nums[mid]) return mid;// nums[mid] == targetelse if(target > nums[mid]){left = mid + 1;// target 在右区间,所以[mid + 1, right]}else{right = mid - 1;// target 在左区间,所以[left, mid - 1]}}// 分别处理如下四种情况// 目标值在数组所有元素之前 [0, -1]// 目标值等于数组中某一个元素 return mid;// 目标值插入数组中的位置 [left, right],return right + 1// 目标值在数组所有元素之后的情况 [left, right], 因为是右闭区间,所以 return right + 1return right + 1;}
}
3.69. x 的平方根 🍊
LeetCode标签:简单
3.1 题目描述🌽
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意: 不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
- 0 < = x < = 2 31 − 1 0 <= x <= 2^{31} - 1 0<=x<=231−1
3.2 题解🍓
-
有人说算法的本质就是数学,这道题目本质就是一道数学题目:如何求得一个非负整数的算数平方根的整数部分
-
在数学上有两种方法来求解这道题目:二分查找和牛顿迭代法,这两种方法的本质就是通过公式不断迭代来逼近目标值
-
二分查找: 由于
x平方根的整数部分mid是满足 k 2 ≤ x k^2≤x k2≤x的最大 k k k值,因此我们可以对 k 进行二分查找,从而得到答案。- 二分查找的下界为 0,上界可以粗略地设定为x。
- 在二分查找的每一步中,我们只需要比较中间元素 mid 的平方与 x 的大小关系,并通过比较的结果调整上下界的范围。
- 由于我们所有的运算都是整数运算,不会存在误差,因此在得到最终的答案 mid 后,也就不需要再去尝试 mid+1了
-
二分查找图解:

-
牛顿迭代法: 说实话这个题目用牛顿法来进行求解就是纯纯的数学题了,涉及到数学上面的推导,做起来还是比较复杂的,如果感兴趣的同学可以参考LeetCode上面的数学推导:牛顿迭代法数学推导,由于这是数学中的一个比较常见的问题,毛毛张在这里直接附上使用牛顿迭代法的计算公式:
- 如果要求 S ( S > 1 ) S\left(S>1\right) S(S>1)的平方根,选取 1 < x 0 < S 1<x_0<S 1<x0<S,其迭代公式为: x n + 1 = 1 2 ( x n + S x n ) x_{n+1}=\frac12\left(x_n+\frac S{x_n}\right) xn+1=21(xn+xnS)
-
牛顿迭代法举例: 求 125348 \sqrt{125348} 125348的算是平方根
 )
) -
同样大家不要忘记了如何使用内置函数和暴力方法进行求解,让我们先看一下最基础的解法是怎么样的,然后再来看二分查找和牛顿迭代法
3.2.1 使用内置函数
class Solution {public int mySqrt(int x) {return (int)Math.sqrt(x);}
}
3.2.2 暴力解法
class Solution {public int mySqrt(int x) {//暴力解法long i =0,square = 0;while(square <= x){i++;square = i * i;}return (int) i-1;}
}
3.2.3 二分查找法
class Solution {public int mySqrt(int x) {//二分查找法int left = 0;int right = x;while(left <= right){int mid = left + (right - left) / 2;long square = (long) mid * mid;if(square > x){right = mid - 1;}else if(square < x){left = mid + 1;}else{return mid;}}return right;}
}
3.2.4 牛顿迭代法
class Solution {public int mySqrt(int x) {if (x == 0) {return 0;}double C = x, x0 = x;while (true) {double xi = 0.5 * (x0 + C / x0);if (Math.abs(x0 - xi) < 1e-7) {break;}x0 = xi;}return (int) x0;}
}
3.3 练习:367. 有效的完全平方数🍒
LeetCode标签:简单
3.3.1 题目描述🍇
给你一个正整数 num 。如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
完全平方数 是一个可以写成某个整数的平方的整数。换句话说,它可以写成某个整数和自身的乘积。
不能使用任何内置的库函数,如 sqrt 。
示例 1:
输入:num = 16
输出:true
解释:返回 true ,因为 4 * 4 = 16 且 4 是一个整数。
示例 2:
输入:num = 14
输出:false
解释:返回 false ,因为 3.742 * 3.742 = 14 但 3.742 不是一个整数。
提示:
- 0 < = x < = 2 31 − 1 0 <= x <= 2^{31} - 1 0<=x<=231−1
3.3.2 题解
- 这道练习和上面一道题目类似,毛毛张就不做过多介绍了,大家根据上面的的方法来进行求解,并且这道题目比上面的一道题目还要简单一些
3.3.2.1 使用内置函数
class Solution {public boolean isPerfectSquare(int num) {//对目标值直接进行开根号,并强制转化为整数int a = (int) Math.sqrt(num);return a * a == num ? true : false;}
}
3.3.2.2 暴力解法
class Solution {public boolean isPerfectSquare(int num) {//暴力解法long i = 1,square = 1;while(square <= num){if(square == num) return true;i++;square = i * i;}return false;}
}
3.3.2.3 二分查找法
class Solution {public boolean isPerfectSquare(int num) {int left = 1;int right = num ;while(left <= right){int mid = (right - left) / 2 + left;//注意,此处求平方一定要进行转换成更大的类型long square = (long) mid * mid;if(square > num){right = mid - 1;}else if(square < num){left = mid + 1;}else{return true;}}return false;}
}
3.3.2.4 牛顿迭代法
class Solution {public boolean isPerfectSquare(int num) {double x0 = num;while (true) {double x1 = (x0 + num / x0) / 2;if (x0 - x1 < 1e-6) {break;}x0 = x1;}int x = (int) x0;return x * x == num;}
}
3.4 注意细节⚠️
- 这道题目在计算的过程中就可能会遇到数据溢出的情况,需要注意,一个地方是二分法中,计算mid值的时候,另一个地方是在计算平方的时候
int mid = (right - left) / 2 + left; //注意,此处求平方一定要进行转换成更大的类型 long square = (long) mid * mid;
4.34. 在排序数组中查找元素的第一个和最后一个位置🍌
LeetCode标签:中等
4.1 题目描述🍍
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
- 0 < = n u m s . l e n g t h < = 1 0 5 0 <= nums.length <= 10^5 0<=nums.length<=105
- − 1 0 9 < = n u m s [ i ] < = 1 0 9 -10^9 <= nums[i] <= 10^9 −109<=nums[i]<=109
nums是一个非递减数组- − 1 0 9 < = t a r g e t < = 1 0 9 -10^9 <= target <= 10^9 −109<=target<=109
4.2 题解🥭
-
很简单的思路就是先找到符合条件的元素,在分别向左边和右边进行搜索,这样就有了我们的暴力解法,但是这样求解的时间负责度和直接从左到右进行查找的时间复杂度本质是相同的,均为 O ( n ) O(n) O(n)
-
这道题目要求时间复杂度为 O ( l o g n ) O(log\ n) O(log n),因此我们就需要使用二分查找法来进行解决, 这道题目也是充分考虑二分查找的特性的题目,第二题使用二分查找法是充分利用循环结束后查找区间的端点值
[min,max],这道题目既要利用这一特性,同时还需要在二分查找的判断语句上下功夫 -
二分法寻找左边界:
if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新rightright = middle - 1;leftBorder = right; } else {left = middle + 1; } -
二分法寻找右边界:
if (nums[middle] > target) {right = middle - 1; } else { // 寻找右边界,nums[middle] == target的时候更新leftleft = middle + 1;rightBorder = left; }
4.2.1 暴力解法
class Solution {public int[] searchRange(int[] nums, int target) {// 创建结果返回值int[] result = { -1, -1 };// 判断特殊情况if (nums == null || nums.length == 0)return result;int left = 0;int right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] == target) {int l = mid, r = mid;// 获取左端点索引while ((l - 1) >= 0 && nums[l - 1] == nums[l]) {l--;}// 获取右端点索引while ((r + 1) <= (nums.length - 1) && nums[r + 1] == nums[r]) {r++;}result[0] = l;result[1] = r;return result;} else if (target > nums[mid]) {left = mid + 1;} else {right = mid - 1;}}return result;}
}
- 这个解法看似使用了二分法,但是其时间复杂度还是 O ( n ) O(n) O(n),还不如直接
for循环进行求解
4.2.2 二分查找写法1
class Solution {int[] searchRange(int[] nums, int target) {int leftBorder = getLeftBorder(nums, target);int rightBorder = getRightBorder(nums, target);// 情况一if (leftBorder == -2 || rightBorder == -2)return new int[] { -1, -1 };// 情况三if (rightBorder - leftBorder > 1)return new int[] { leftBorder + 1, rightBorder - 1 };// 情况二return new int[] { -1, -1 };}int getRightBorder(int[] nums, int target) {int left = 0;int right = nums.length - 1;int rightBorder = -2; // 记录一下rightBorder没有被赋值的情况while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] > target) {right = middle - 1;} else { // 寻找右边界,nums[middle] == target的时候更新leftleft = middle + 1;rightBorder = left;}}return rightBorder;}int getLeftBorder(int[] nums, int target) {int left = 0;int right = nums.length - 1;int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况while (left <= right) {int middle = left + ((right - left) / 2);if (nums[middle] >= target) { // 寻找左边界,nums[middle] == target的时候更新rightright = middle - 1;leftBorder = right;} else {left = middle + 1;}}return leftBorder;}
}
- 上面的写法比较复杂,因此我们在先如何将上面的寻找左边界和右边界进行统一,于是我们可以在二分查找的函数中加上一个标志位,这样就能把两种方式进行统一,于是就有了下面的写法2
4.2.3 二分查找写法2
class Solution {public int[] searchRange(int[] nums, int target) {//左边界int leftIdx = binarySearch(nums,target,false);int rightIdx = binarySearch(nums,target,true) - 1;if (leftIdx <= rightIdx && rightIdx < nums.length) {return new int[]{leftIdx, rightIdx};} return new int[]{-1, -1};}//二分查找public int binarySearch(int[] nums,int target,boolean flag){//flag用来标志查找左边界还是右边界int left = 0;int right = nums.length-1;while(left <= right){int mid = left + (right - left) / 2;if(target > nums[mid] || (flag && target >= nums[mid])){left = mid + 1;}else{right = mid - 1;}}return left;}
}
5.总结🌍
- 相信通过上面四道题目+一道练习,大家可以算是对二分法的特性有了初步的了解,但是,上面的几道题目仅仅二分法中比较简单的题目
- 如果想练习更多二分法的题目可以点击此处进行跳转:宫水三叶二分法类型题解


参考文献🎁
- LeetCode官网
- 代码随想录
相关文章:

LeetCode每日练习 | 二分查找 | 数组 |Java | 图解算法
🙋大家好!我是毛毛张! 🌈个人首页: 神马都会亿点点的毛毛张 📌 你真的刷明白了二分查找吗⁉️记得看毛毛张每个题目中写的【注意细节】⚠️ 文章目录 0.前言🍁1.[704. 二分查找🍍](https://l…...

2024年获客新渠道,大数据爬虫获客:技术实现精准抓取数据资源
**2024年获客新渠道:大数据爬虫获客及技术实现精准抓取数据资源** ### 一、大数据爬虫获客概述 在2024年,随着大数据技术的不断发展和互联网的普及,大数据爬虫获客已经成为企业获取客户信息、实现精准营销的重要渠道。爬虫技术通过自动化程…...

滑模变结构控制仿真实例(s-function代码详解)
目录 一、建立系统数学模型二、控制器设计1. 设计滑模面(切换面)2.设计控制器 u3. 稳定性证明 三、 Matlab 仿真1. s-function 模型2. 主要代码3. 仿真结果(采用符号函数sign(s))4. 仿真结果(采用饱和函数sat(s)) 一、建立系统数学模型 { x ˙ 1 x 2 x ˙ 2 x 3 x ˙ 3 x 1 …...

MySQL处理引擎
MySQL中的数据用各种不同的技术存储在文件(或者内存)中。这些技术中的每一种都 使用不同的存储机制、索引技巧、锁定水平并且最终提供广泛的、不同的功能和能力。通过 选择不同的技术,能够获得额外的速度或者功能,从而改善应用的整体性能。 这些不同的技…...

HTTP 方法详解:GET、POST 和 PUT
HTTP 方法详解:GET、POST 和 PUT HTTP 方法(GET、POST、PUT)用于客户端和服务器之间的通信。它们在输入、输出和传输内容上有显著区别。 1. GET 方法 – 获取资源 用途:从服务器获取资源。 输入: 请求行ÿ…...

被工信部认可的开源软件治理解决方案
近日,工信部网络安全产业发展中心正式发布了“2023年信息技术应用创新解决方案”,开源网安凭借“基于SCA技术开源软件治理解决方案”顺利入选,成为经工信部认可的优秀解决方案,这是开源网安连续两届荣获此荣誉。 工业和信息化部网…...

文件包含漏洞--pyload
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 一.PHP伪协议利用 php://协议 php://filter :用于在读取作用和写入文件时进行过滤和转换操作。 作用1:利用base64编码过滤器读取源码 通常利用文件包含执行php://filte…...

C++包管理之`vcpkg`简介
文章目录 工程文件安装vcpkg安装fmt库安装全局的库安装仅该工程使用的库 在CMake中使用vcpkg通过CMAKE_TOOLCHAIN_FILE使用vcpkg通过CMakePresets.json使用vcpkg 在C开发中,我们经常会使用一些第三方库,比如说Boost、fmt、spdlog等等。这些库的安装和使用…...

【机器学习】必会核函数之:高斯核函数
高斯核函数 1、引言2、高斯核函数2.1 定义2.2 核心原理2.3 应用场景2.4 代码示例3、总结1、引言 在机器学习和数据科学领域,核方法 ( K e r n e l M e t h o d s ) (Kernel Methods) (Kerne...

51单片机和STM32区别
51单片机和 STM32 区别 51单片机和 STM32 是两种常见的微控制器,它们在架构、性能、外设接口、功耗和开发环境等方面有所不同。 1. 架构差异 51单片机基于传统的哈佛总线结构,采用 CISC 架构,而 STM32 基于 ARM Cortex-M 系列的32位处理器核…...

Python 伪随机数生成器
random.sample() 函数原理 在 Python 中,随机数的生成通常依赖于伪随机数生成器(PRNG)。random 模块提供了一个易于使用的接口来生成伪随机数。以下是 random 模块中随机数生成的基本原理和方法: 伪随机数生成器(PRN…...
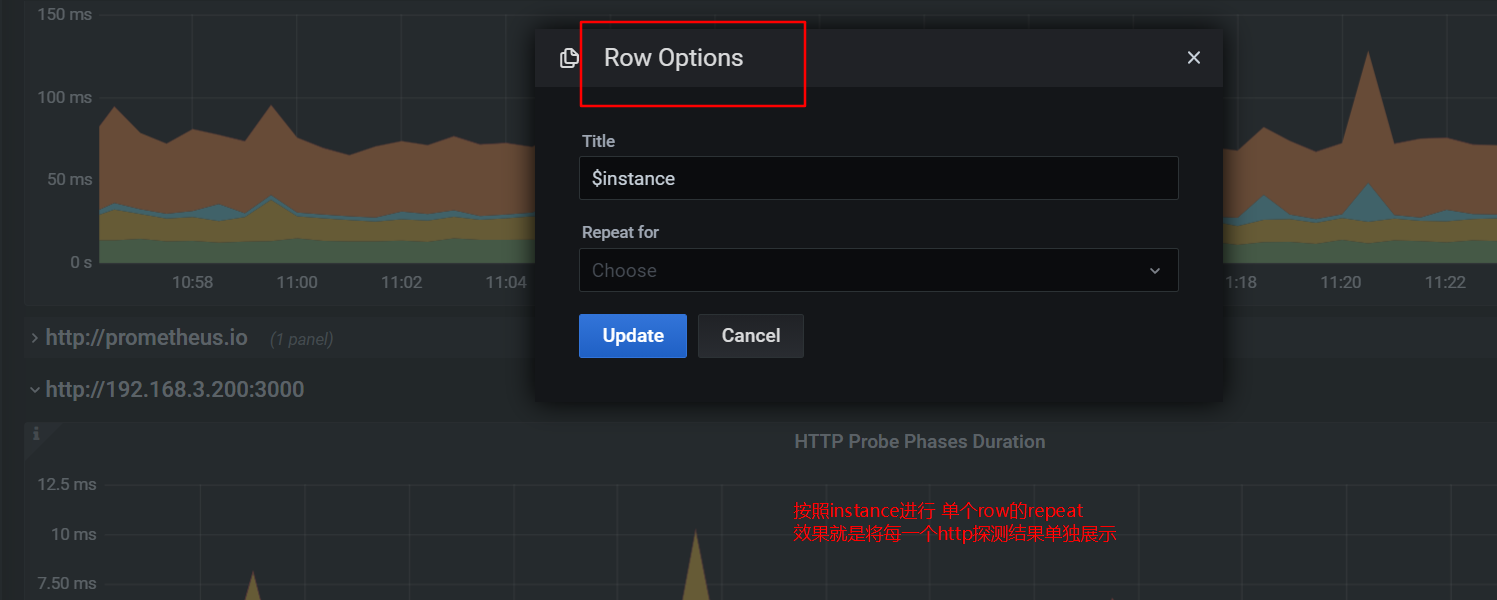
7.5 grafana上导入模板看图并讲解告警
本节重点介绍 : blackbox_exporter grafana大盘导入和查看告警配置讲解 grafana大盘 grafana 上导入 blackbox_exporter dashboard 地址 https://grafana.com/grafana/dashboards/13659举例图片http总览图value_mapping设置 展示设置阈值,展示不同背景色 告警配…...

BUG解决(vue3+echart报错):Cannot read properties of undefined (reading ‘type‘)
这是 vue3echart5 遇到的报错:Cannot read properties of undefined (reading ‘type‘) 这个问题需要搞清楚两个关键方法: toRaw: 作用:将一个由reactive生成的响应式对象转为普通对象。 使用场景: 用于读取响应式…...

VSCode+git的gitee仓库搭建
在此之前你已经在gitee创建好了账号,并新建了一个仓库。 1. 安装 Visual Studio Code Visual Studio Code 是编辑 Markdown 和站点配置文件的基础,以下将其简称为 VSCode,你可以在它的 官方网站 下载到它。 如若不理解各个版本之间的区别…...

Golang | Leetcode Golang题解之第297题二叉树的序列化与反序列化
题目: 题解: type Codec struct{}func Constructor() (_ Codec) {return }func (c Codec) serialize(root *TreeNode) string {if root nil {return "X"}left : "(" c.serialize(root.Left) ")"right : "("…...

交叉熵和MSE的区别
交叉熵 交叉熵损失通常用于分类问题,尤其是二分类和多分类问题。它度量的是预测概率分布与真实标签概率分布之间的差异。 适用于分类问题。常用于神经网络中的Softmax层之后作为损失函数。适用于二分类、多分类中的模型优化(如图像分类、文本分类等&am…...

具身智能又进一步!卡内基梅隆Meta苏黎世联邦实现虚拟人超灵活抓取
论文链接:https://arxiv.org/pdf/2407.11385 github链接:https://www.zhengyiluo.com/Omnigrasp-Site/ 亮点直击 本文设计了一种灵巧且通用的人形机器人运动表示,这显著提高了样本效率,并使得通过简单而有效的状态和奖励设计来学习…...

嘉盛:货币政策走向与市场预期
在当前经济背景下,美联储的政策决策备受关注。尽管本周的会议可能不会带来实质性利率变动,但其后的走向可能对未来产生深远影响。市场预期与政策走向 随着近几个月大量通胀数据公布,市场普遍预计,美联储将为即将到来的降息措施奠定…...

[C#]基于wpf实现的一百多种音色的Midi键盘软件
键盘 音色库 源码地址:https://download.csdn.net/download/FL1623863129/89599322...

关于香橙派系统烧录,1.1.8或者1.1.10两个版本都无法启动Orangepi5
先执行 git clone https://github.com/orangepi-xunlong/orangepi-build.gitgit log 默认会显示较新的提交记录。如果你需要查看更多的提交记录,可以使用以下方法: git log --oneline --graph --all这会以简洁的方式显示所有分支的提交记录,…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...
