【C++/STL】:哈希的应用 -- 位图布隆过滤器
目录
- 🚀🚀前言
- 一,位图
- 1. 位图的概念
- 2. STL库中的位图
- 3. 位图的设计
- 4. 位图的模拟实现
- 5. 位图的优缺点
- 6. 位图相关考察题⽬
- 二,布隆过滤器
- 1. 布隆过滤器的概念
- 2. 布隆过滤器的实现
- 3. 布隆过滤器删除问题
- 4. 布隆过滤器的优缺点
点击跳转至文章: 【C++/STL】:哈希 – 线性探测&哈希桶
🚀🚀前言
在前面的文章里我们已经学习了什么是哈希和以哈希表为底层的unordered系列容器的使用。本篇文章的位图&布隆过滤器也是哈希思想下的产物,经常使用它们来解决有关海量数据的问题。
一,位图
1. 位图的概念
在引出位图的概念之前,先来看一个经典面试题:

深入分析:
解题思路2是否可行,我们先算算40亿个数据⼤概需要多少内存。
1G = 1024MB =1024 * 1024KB = 1024*1024 * 1024byte约等于10亿多byte,那么40亿个整数约等于16G,说明40亿个数是无法直接放到内存中的,只能放到硬盘文件中。而二分查找只能对内存数组中的有序数据进行查找。
解题思路3:数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使⽤⼀个⼆进制⽐特位来代表数据是否存在的信息,如果⼆进制⽐特位为1,代表存在,为0代表不存在。
那么我们设计⼀个⽤二进制比特位表⽰数据是否存在的数据结构,这个数据结构就叫位图。
2. STL库中的位图

根据文档可知,位图bitset 是非类型模板,N是指需要多少比特位。使用时需要包含头文件:
#include <bitset>
位图常用的核心接口主要有三个:
(1) x 映射位标记成1(插入 x,有这个数据了)

(2) x 映射位标记成0(删除 x,没有这个数据了)

(3) 检查是否存在这个数据
x映射的位是1,返回真
x映射的位是0,返回假

3. 位图的设计
位图本质是⼀个直接定址法的哈希表,每个整型值映射⼀个bit位,位图提供控制这个bit的相关接口。
实现中需要注意的是,C/C++没有对应位的类型,只能看int/char这样整形类型,我们再通过位运算去控制对应的⽐特位。⽐如我们数据存到vector< int >中,相当于每个int值映射对应的32个值,⽐如第⼀个整形映射0-31对应的位,第⼆个整形映射32-63对应的位,后⾯的以此类推,那么来了⼀个整形值x,i = x / 32;j = x % 32;计算出x映射的值在vector的第 i 个整形数据的第 j 位。

4. 位图的模拟实现
#include<vector>//非类型模板参数。需要多少比特位
template <size_t N>
class bitset
{
public:bitset(){_bs.resize(N / 32 + 1);}//x映射位标记成1void set(size_t x){//映射的位置:第i个整型数据的第j位size_t i = x / 32;size_t j = x % 32;_bs[i] |= (1 << j);}//x映射位标记成0void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_bs[i] &= (~(1 << j));}//x映射的位是1,返回真//x映射的位是0,返回假bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _bs[i] & (1 << j);}
private:vector<size_t> _bs;
};5. 位图的优缺点
优点:增删查改快,节省空间
缺点:只适⽤于整形
6. 位图相关考察题⽬

深入分析:
第一题和第三题是同一类型的题,我们先来分析这两题。首先我们知道把数据放入位图中只能标记在或不在两种状态,而题目要求的是找出出现几次的数据,可能是出现0次,1次……,显然单用一个位图的一个比特位是无法满足的。
用两个位图的标记就可以解决。我们规定00表示数据出现0次,01表示数据出现1次,10表示数据出现2次,11表示数据出现3次及以上
代码实现如下:
注意:这里用的bitset是上文我们自己实现的bitset。
我们针对第一题和第三题设计一个结构:
template<size_t N>
class twobitset
{
public:void set(size_t x){bool bit1 = _bs1.test(x);bool bit2 = _bs2.test(x);if (!bit1 && !bit2) // 00->01{_bs2.set(x);}else if (!bit1 && bit2) // 01->10{_bs1.set(x);_bs2.reset(x);}else if (bit1 && !bit2) // 10->11{_bs1.set(x);_bs2.set(x);}}// 返回0 出现0次数// 返回1 出现1次数// 返回2 出现2次数// 返回3 出现2次及以上int get_count(size_t x){bool bit1 = _bs1.test(x);bool bit2 = _bs2.test(x);if (!bit1 && !bit2){return 0;}else if (!bit1 && bit2){return 1;}else if (bit1 && !bit2){return 2;}else{return 3;}}private:bitset<N> _bs1;bitset<N> _bs2;
};//测试代码,可以统计出100以内哪个数据出现了几次
void test_twobitset()
{twobitset<100> tbs; //开100个bit位int a[] = { 5,7,9,2,5,99,5,5,7,5,3,9,2,55,1,5,6,6,6,6,7,9 };for (auto e : a){tbs.set(e);}for (size_t i = 0; i < 100; ++i){cout << i << "->" << tbs.get_count(i) << endl;//if (tbs.get_count(i) == 1 || tbs.get_count(i) == 2)//cout << i << endl;}
}
第二题的代码实现:
把数据分别放入两个位图中,如果两个位图的标记均为1,说明都存在,就是二者的交集。
void test_bitset1()
{int a1[] = { 5,7,9,2,5,99,5,5,7,5,3,9,2,55,1,5,6 };int a2[] = { 5,3,5,99,6,99,33,66 };bit::bitset<100> bs1;bit::bitset<100> bs2;for (auto e : a1)bs1.set(e);for (auto e : a2)bs2.set(e);for (size_t i = 0; i < 100; i++){if (bs1.test(i) && bs2.test(i))cout << i << endl;}
}

二,布隆过滤器
有⼀些场景下⾯,有⼤量数据需要判断是否存在,⽽这些数据不是整形,那么位图就不能使⽤了,使⽤红⿊树/哈希表等内存空间可能不够。这些场景就需要布隆过滤器来解决。
1. 布隆过滤器的概念
布隆过滤器是⼀种可以⽤来告诉你"某样东西⼀定不存在或者可能存在"的数据结构,它是⽤多个哈希函数,将⼀个数据映射到位图结构中。
布隆过滤器的思路就是把key先映射转成哈希整型值,再映射⼀个位,如果只映射⼀个位的话,冲突率会⽐较多,所以可以通过多个哈希函数映射多个位,降低冲突率。
布隆过滤器这⾥跟哈希表不⼀样,它⽆法解决哈希冲突的,因为他压根就不存储这个值,只标记映射的位。它的思路是尽可能降低哈希冲突。判断⼀个值key在是不准确的,判断⼀个值key不在是准确的。
2. 布隆过滤器的实现
说明:我们这里用的bitset是我们上文自己实现的bitset,不是库里的。
#include "BitSet.h"
#include <string>struct HashFuncBKDR
{size_t operator()(const std::string& s){size_t hash = 0;for (auto ch : s){hash *= 31;hash += ch;}return hash;}
};struct HashFuncAP
{ size_t operator()(const std::string& s){size_t hash = 0;for (size_t i = 0; i < s.size(); i++){if ((i & 1) == 0) // 偶数位字符hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));else // 奇数位字符hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >> 5)));}return hash;}
};struct HashFuncDJB
{size_t operator()(const std::string& s){size_t hash = 5381;for (auto ch : s)hash = hash * 33 ^ ch;return hash;}
};//要用多个哈希函数多映射几个位,以便降低哈希冲突
template <size_t N,size_t X = 5,class K = string,class Hash1 = HashFuncBKDR,class Hash2 = HashFuncAP,class Hash3 = HashFuncDJB>
class BloomFilter
{
public:void Set(const K& key){size_t hash1 = Hash1()(key) % M;size_t hash2 = Hash2()(key) % M;size_t hash3 = Hash3()(key) % M;_bs.set(hash1);_bs.set(hash2);_bs.set(hash3);}//如果其中一个位为0,就确定不在,如果都为1,那就在(存在误判)bool Test(const K& key){size_t hash1 = Hash1()(key) % M;if (!_bs.test(hash1))return false;size_t hash2 = Hash2()(key) % M;if (!_bs.test(hash2))return false;size_t hash3 = Hash3()(key) % M;if (!_bs.test(hash3))return false;return true;}
private:static const size_t M = N * X; //布隆过滤器的bit长度bit::bitset<M> _bs;
};//测试代码
void TestBloomFilter1()
{BloomFilter<10> bf;bf.Set("猪八戒");bf.Set("孙悟空");bf.Set("唐僧");cout << bf.Test("猪八戒") << endl;cout << bf.Test("孙悟空") << endl;cout << bf.Test("唐僧") << endl;cout << bf.Test("沙僧") << endl;cout << bf.Test("猪八戒1") << endl;cout << bf.Test("猪戒八") << endl;
}

3. 布隆过滤器删除问题
布隆过滤器默认是不⽀持删除的,因为⽐如"猪⼋戒“和”孙悟空“都映射在布隆过滤器中,他们映射的位有⼀个位是共同映射的(冲突的),如果我们把孙悟空删掉,那么再去查找“猪⼋戒”会查找不到,因为那么“猪⼋戒”间接被删掉了。
4. 布隆过滤器的优缺点
优点:增删查改快,节省空间
缺点:只适⽤于整形
相关文章:

【C++/STL】:哈希的应用 -- 位图布隆过滤器
目录 🚀🚀前言一,位图1. 位图的概念2. STL库中的位图3. 位图的设计4. 位图的模拟实现5. 位图的优缺点6. 位图相关考察题⽬ 二,布隆过滤器1. 布隆过滤器的概念2. 布隆过滤器的实现3. 布隆过滤器删除问题4. 布隆过滤器的优缺点 点击…...
非线性面板数据实证模型及 Stata 具体操作步骤
目录 一、引言 二、文献综述 三、理论原理 四、实证模型 五、稳健性检验 六、程序代码及解释 一、引言 在当今的经济和社会研究中,非线性面板数据模型的应用日益广泛。这类模型能够更好地捕捉数据中的复杂关系,为研究者提供更深入和准确的分析结果。…...

视角 | 麻省理工学院提出出温度计校准法,专治AI大模型过度自信
在数字化浪潮的推动下,人工智能(AI)正成为塑造未来的关键力量。硅纪元视角栏目紧跟AI科技的最新发展,捕捉行业动态;提供深入的新闻解读,助您洞悉技术背后的逻辑;汇聚行业专家的见解,…...
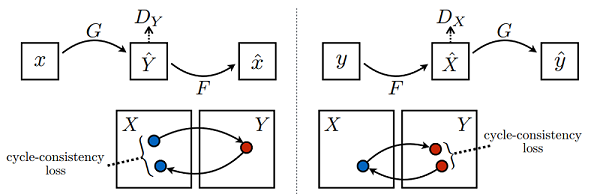
昇思25天学习打卡营第XX天|CycleGAN图像风格迁移互换
CycleGAN是一种用于图像到图像翻译的生成对抗网络,它突破了传统域迁移模型的限制,无需成对样本即可学习图像在不同域间的转换。这种无监督的方法特别适用于难以获取配对数据的场景,例如艺术风格迁移。与需要成对训练样本的Pix2Pix不同&#x…...

嵌入式Linux学习: interrupt实验
Linux中的Interrupt(中断)系统是一个至关重要的组成部分,它负责管理和处理系统中发生的各种硬件和软件中断,确保系统能够正确响应外部设备的请求,保持系统的稳定性和可靠性。 1.中断的作用 允许设备在没有CPU干预的情…...

GPT-4o mini 来袭:开发者如何驾驭新一代AI模型?
GPT-4o Mini 来袭:开发者如何驾驭新一代 AI 模型? 引言 随着人工智能(AI)技术的飞速发展,越来越多的先进模型不断涌现,给各行各业带来了深远的影响。OpenAI 最新推出的 GPT-4o Mini 是一种创新的 AI 模型…...

校园点餐系统
1 项目介绍 1.1 摘要 在这个被海量信息淹没的数字化时代,互联网技术以惊人的速度迭代,信息的触角无处不在,社会的脉动随之加速。每一天,我们都被汹涌而至的数据浪潮包裹,生活在一个全方位的数字信息矩阵中。互联网的…...

进口不锈钢309S螺栓的应用优势
进口不锈钢309S螺栓因其优异的性能和广泛的应用范围而在许多行业中备受青睐。309S不锈钢是一种含硫的易切削不锈钢,具有良好的耐高温和耐腐蚀性能,使其成为高温环境下理想的选择。下面我们就来详细探讨一下进口不锈钢309S螺栓的应用优势。 一、309S不锈钢…...

C# 设计模式之工厂方法模式
总目录 前言 本文是个人基于C#学习设计模式总结的学习笔记,希望对你有用! 在简单工厂模式中说到了简单工厂模式的缺点:简单工厂模式系统难以扩展,一旦添加新产品就不得不修改简单工厂方法,这样就会造成简单工厂的实现…...

Webpack 从入门到精通
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 一、Webpack 简介 二、Webpack 的核心概念 三、Webpack 的安装与配置 安装 Node.js 安装 Webpack 初始…...

基于VScode和C++ 实现Protobuf数据格式的通信
目录 1. Protobuf 概述1.1 定义1.2Protobuf的优势 2. Protobuf 语法3、序列号和反序列化3.1 .pb.h 头文件3.2 序列化3.3 反序列化 4、测试用例 Protobuf详细讲解链接 1. Protobuf 概述 1.1 定义 protobuf也叫protocol buffer是google 的一种数据交换的格式,它独立…...

linux环境openssl升级
1、下载openssl https://openssl-library.org/source/ 或者通过wget --no-check-certificate https://www.openssl.org/source/openssl-3.0.13.tar.gz 2、解压openssl tar -zxvf openssl-3.0.13.tar.gz 3、切换到解压后的目录 cd openssl-3.0.13/ 4、配置openssl安装目录…...

150Kg载重遥控履带式无人车技术详解
150Kg载重遥控履带式无人车是一种专为复杂地形和重载运输设计的无人化智能平台。它结合了先进的动力技术、履带式行走机构、远程遥控系统、高精度感知与导航技术及模块化设计,能够在恶劣环境下执行物资运输、侦察监视、灾害救援等多种任务。该车以其卓越的越野能力、…...

STM32的外部中断详解
一、什么是中断? 想象一下你正在家里做饭,突然门铃响了,你听到门铃声后,会暂时放下手中的事情(比如炒菜),去开门看看是谁。在这个例子中,门铃声就是一个“中断”,它打断…...

关于python问题 ,生成的excel文件内无爬取的数据存在,请问应如何解决?
🏆本文收录于《CSDN问答解惑-专业版》专栏,主要记录项目实战过程中的Bug之前因后果及提供真实有效的解决方案,希望能够助你一臂之力,帮你早日登顶实现财富自由🚀;同时,欢迎大家关注&&收…...

详细介绍Avalonia中的文件操作StorageProvider服务
文章目录 一、介绍二、StorageProvider的原理三、StorageProvider的实现1. 创建文件选择和保存对话框2. 选择目录四、StorageProvider的配置五、StorageProvider的高级用法1. 读取和写入文件2. 获取文件和目录信息3. 管理文件和目录4. 处理不同平台的差异六、总结一、介绍 在桌…...

「7.31更新日志」JVS·智能BI、逻辑、规则引擎功能更新说明
项目介绍 JVS是企业级数字化服务构建的基础脚手架,主要解决企业信息化项目交付难、实施效率低、开发成本高的问题,采用微服务配置化的方式,提供了 低代码数据分析物联网的核心能力产品,并构建了协同办公、企业常用的管理工具等&am…...

编程语言 | C | 代码整理 | 4月
八月拍了拍你,并对你说:“好运就要开始了”! 目录 编程语言 | C | 代码整理 | 4月2019/4/12019/4/22019/4/22019/4/32019/4/42019/4/52019/4/62019/4/72019/4/82019/4/92019/4/102019/4/112019/4/122019/4/132019/4/142019/4/152019/4/162019…...

模板可变参数
当涉及到 C 编程中的模板参数处理时,特别是在处理可变数量的参数时,模板可变参数(variadic templates)是一个非常有用的特性。本篇博客将深入介绍模板可变参数的基本概念、语法、应用场景以及示例代码,帮助读者理解如何…...

是你!是你!我们的黄金写手!
...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

