dp:221. 最大正方形
221. 最大正方形

看到这个题目真能立马想到dp吗?貌似很难,即使知道是一个dp题也很难想到解法。
直观来看,使用bfs以一个点为中点进行遍历,需要的时间复杂度为 O ( n 2 m 2 ) O(n^2m^2) O(n2m2)
但是可以很容易发现,如果求以一个点为角 构成的最大正方形,可以通过其他周围的点作为角来快速找到这个点的最大正方形。
我们用数组存以该点为右下角,左下角,左上角,右上角的最大正方形,可以通过周围的转移,然后求出以它为“中心”构成的最大正方形。于是有如下代码
class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int n = matrix.size();int m = matrix[0].size();if(n == 1 && m == 1) return matrix[0][0];vector<vector<vector<int>>> dp(n, vector<int>(m, vector<int>(4, 0)));int ans = 0;for(int j = 0; j < m; ++ j){dp[0][j][0] = dp[0][j][1]= dp[0][j][2] = dp[0][j][3] = matrix[0][j];}for(int i = 1; i < n - 1; ++ i){dp[i][0][0] = dp[i][0][1] = dp[i][0][2] = dp[i][0][3] = matrix[i][0];for(int j = 1; j < m - 1; ++ j){dp[i][j][0] = min(dp[i - 1][j][0], min(dp[i - 1][j - 1][0], dp[i][j - 1][0])) + 1;dp[i][j][1] = min(dp[i - 1][j][1], min(dp[i - 1][j + 1][1], dp[i][j + 1][1])) + 1;····}//最后一列}//最后一行return ans * ans;}
};
但是实际上,以该点为右下角就足以解决这个问题,因为对于任何一个最大正方形而言,它一定有一个右下角,那么找到这个右下角能构成的最大正方形就是这个正方形了。
class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {int n = matrix.size();int m = matrix[0].size();if(n == 1 && m == 1) return matrix[0][0] - '0';vector<vector<int>> dp(n, vector<int>(m, 0));int ans = 0;for(int i = 0; i < m; ++ i){dp[0][i] = matrix[0][i] - '0';ans = max(ans, dp[0][i]);}for(int i = 1; i < n; ++ i){dp[i][0] = matrix[i][0] - '0';ans = max(ans, dp[i][0]);for(int j = 1; j < m; ++ j){if(matrix[i][j] == '0') dp[i][j] = 0;else dp[i][j] = min(dp[i - 1][j], min(dp[i][j - 1], dp[i - 1][j - 1])) + 1;ans = max(ans, dp[i][j]);}}return ans * ans;}
};
相关文章:

dp:221. 最大正方形
221. 最大正方形 看到这个题目真能立马想到dp吗?貌似很难,即使知道是一个dp题也很难想到解法。 直观来看,使用bfs以一个点为中点进行遍历,需要的时间复杂度为 O ( n 2 m 2 ) O(n^2m^2) O(n2m2) 但是可以很容易发现,…...

花10分钟写个漂亮的后端API接口模板!
你好,我是田哥 在这微服务架构盛行的黄金时段,加上越来越多的前后端分离,导致后端API接口规范变得越来越重要了。 比如:统一返回参数形式、统一返回码、统一异常处理、集成swagger等。 目的主要是规范后端项目代码,以及…...
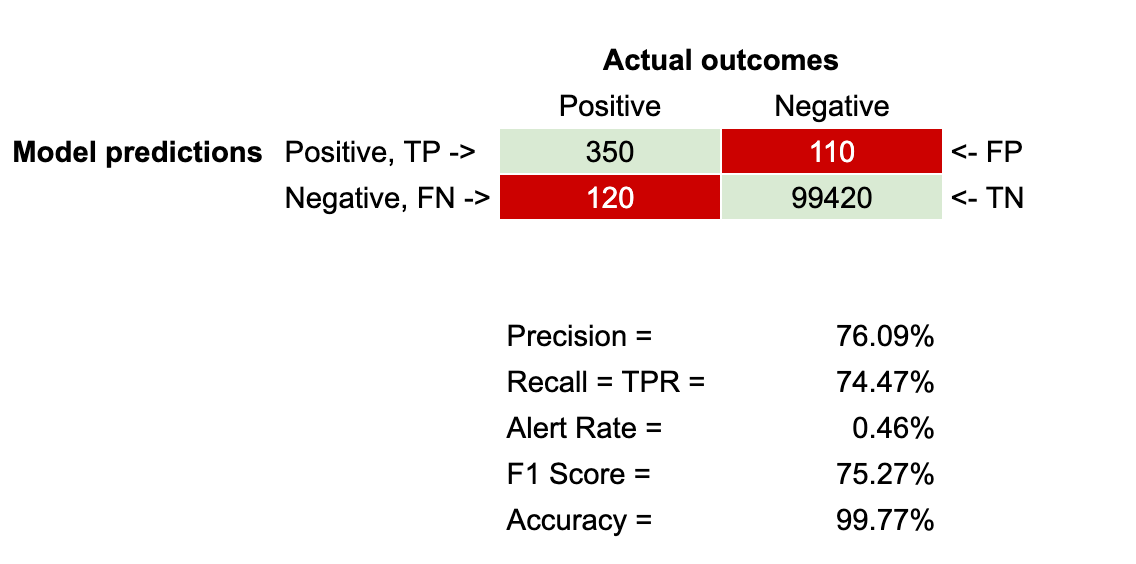
评估分类机器学习模型的指标
欢迎来到雲闪世界。一旦我们训练了一个监督机器学习模型来解决分类问题,如果这就是我们工作的结束,我们会很高兴,我们可以直接向他们输入新数据。我们希望它能正确地对所有内容进行分类。然而,实际上,模型做出的预测并…...

农机自动化:现代农业的未来趋势
随着人口的增长和农业生产的需求不断增加,提高农业生产效率成为现代农业的重要目标。农机自动化作为一种新兴技术,可以大幅度提升农机的使用效率和生产能力。农机自动化是指利用先进的传感技术、数据处理和人工智能技术,使农机能够自动完成农…...

25考研操作系统复习·1.1/1.2/1.3 操作系统的基本概念/发展历程/运行环境
目录 操作系统的基本概念 概念(定义) 功能和目标 资源的管理者 向上层提供服务 给普通用户的 给软件/程序员的 对硬件机器的拓展 操作系统的特征 操作系统的发展历程 操作系统的运行环境 操作系统的运行机制 中断和异常 中断的作用 中断的…...

如何培养学生的创新意识和实践能力
培养学生的创新意识和实践能力是一个复杂而系统的过程,涉及多个方面的努力和措施。以下是一些具体的做法: 一、培养学生的创新意识 提供创新环境: 为学生创造一个开放、自由、支持创新的学习环境,让他们能够自由地表达自己的想法…...
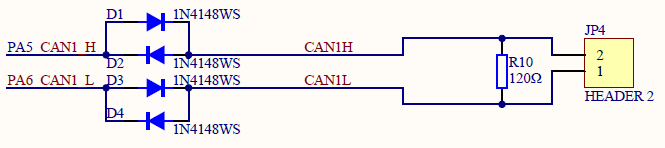
四、GD32 MCU 常见外设介绍(15)CAN 模块介绍
CAN是控制器局域网络(Controller Area Network)的简称,它是由研发和生产汽车电子产品著称的德国BOSCH公司开发的,并最终成为国际标准(ISO11519),是国际上应用最广泛的现场总线之一。 CAN总线协议已经成为汽车计算机控…...

AIGC大模型产品经理高频面试大揭秘‼️
近期有十几个学生在面试大模型产品经理(薪资还可以,详情见下图),根据他们面试(包括1-4面)中出现高频大于3次的问题汇总如下,一共32道题目(有答案)。 29.讲讲T5和Bart的区…...

【嵌入式笔记】【C语言】struct union
结构体(Struct)定义: struct 结构体名 {member1; // 成员1,可以是任何基本数据类型或复合类型member2; // 成员2... };//例如: struct Point {float x;float y;...
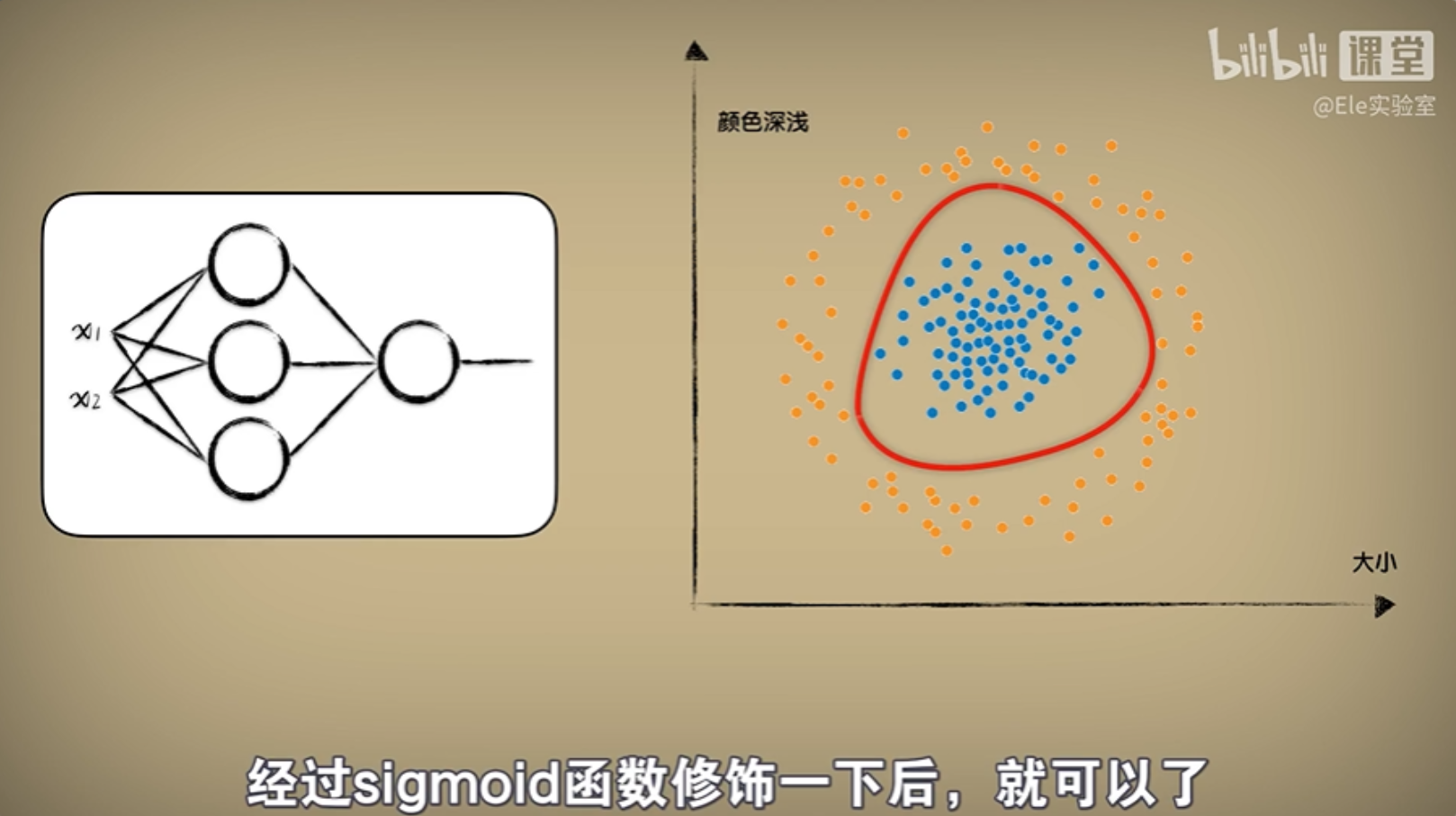
【初学人工智能原理】【9】深度学习:神奇的DeepLearning
前言 本文教程均来自b站【小白也能听懂的人工智能原理】,感兴趣的可自行到b站观看。 代码及工具箱 本专栏的代码和工具函数已经上传到GitHub:1571859588/xiaobai_AI: 零基础入门人工智能 (github.com),可以找到对应课程的代码 正文 深度…...

[RoarCTF 2019]Easy Calc1
打开题目 查看源码,看到 看到源代码有 calc.php,构造url打开 看到php审计代码, 由于页面中无法上传num,则输入 num,在num前加入一个空格可以让num变得可以上传,而且在进行代码解析时,php会把前…...
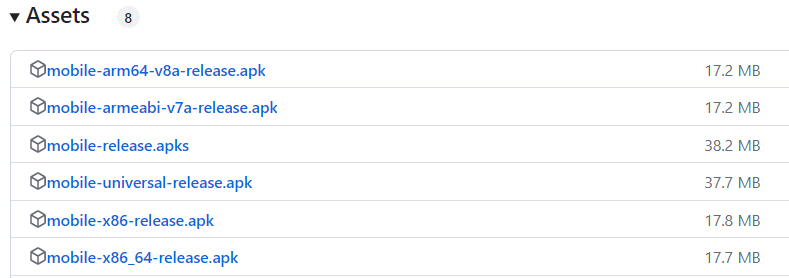
安卓APK安装包arm64-v8a、armeabi-v7a、x86、x86_64有何区别?如何选择?
在GitHub网站下载Android 安装包,Actions资源下的APK文件通常有以下版本供选择: 例如上图是某Android客户端的安装包文件,有以下几个版本可以选择: mobile-release.apk(通用版本,体积最大)mobi…...

【AI大模型】通义千问:开启语言模型新篇章与Function Call技术的应用探索
文章目录 前言一、大语言模型1.大模型介绍2.大模型的发展历程3.大模型的分类a.按内容分类b.按应用分类 二、通义千问1.通义千问模型介绍a.通义千问模型介绍b.应用场景c.模型概览 2.对话a.对话的两种方式通义千问API的使用 b.单轮对话Vue页面代码:Django接口代码 c.多…...

详细教程 MySQL 数据库 下载 安装 连接 环境配置 全面
数据库就是储存和管理数据的仓库,对数据进行增删改查操作,其本质是一个软件。 首先数据有两种,一种是关系型数据库,另一种是非关系型数据库。 关系型数据库是以表的形式来存储数据,表和表之间可以有很多复杂的关系&a…...

门控循环单元GRU
目录 一、GRU提出的背景:1.RNN存在的问题:2.GRU的思想: 二、更新门和重置门:三、GRU网络架构:1.更新门和重置门如何发挥作用:1.1候选隐藏状态H~t:1.2隐藏状态Ht: 2.GRU: 四、底层源码…...

程序员修炼之路
成为一名优秀的程序员,需要广泛而深入地学习多个领域的知识。这些课程不仅帮助建立扎实的编程基础,还培养了问题解决、算法设计、系统思维等多方面的能力。以下是一些核心的必修课: 计算机基础 计算机组成原理:理解计算机的硬件组…...

PHP时间相关函数
时间、日期 time()获取当前时间戳(10位)microtime(true)返回一个浮点时间戳data(格式,时间戳)日期格式化 $time time(); echo date(Y-m-d H:i:s, $time);strtotime&am…...

python进阶——python面向对象
前言 Python是一种面向对象的编程语言,可在Python中使用类和对象来组织和封装代码。面向对象编程(OOP)是一种编程范例,它将数据和操作数据的方法封装在一个对象内部,通过对象之间的交互来实现程序的功能。 1、面向对象…...

【无标题】vue2鼠标悬停(hover)时切换图片
在Vue 2中,要实现鼠标悬停(hover)时切换图片的功能,你不能直接在模板的:src绑定中处理这个逻辑,因为Vue的模板不支持条件渲染的复杂逻辑(如基于鼠标状态的动态图片切换)。但是,你可以…...
- 分析法)
每天一个数据分析题(四百五十九)- 分析法
故障树分析法经常与哪些方法联合使用? A. 头脑风暴法 B. 五问法 C. 配对法 D. 引力法 数据分析认证考试介绍:点击进入 题目来源于CDA模拟题库 点击此处获取答案 数据分析专项练习题库 内容涵盖Python,SQL,统计学…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
