【注意力MHA,MQA,GQA,MLA】
注意力机制优化简明图解
1. 多头注意力(MHA)
图示:
Input --> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Attention Head N]--> [Concatenate] --> Output
公式:
Output = Concat ( head 1 , head 2 , … , head N ) \text{Output} = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_N) Output=Concat(head1,head2,…,headN)
head i = Attention ( Q , K , V ) \text{head}_i = \text{Attention}(Q, K, V) headi=Attention(Q,K,V)
2. 多查询注意力(MQA)
图示:
Input --> [Shared Keys & Values]--> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Concatenate] --> Output
公式:
Output = Concat ( head 1 , head 2 , … , head N ) \text{Output} = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_N) Output=Concat(head1,head2,…,headN)
head i = Attention ( Q , K shared , V shared ) \text{head}_i = \text{Attention}(Q, K_{\text{shared}}, V_{\text{shared}}) headi=Attention(Q,Kshared,Vshared)
3. 分组查询注意力(GQA)
图示:
Input --> [Attention Group 1]--> [Attention Group 2]--> ...--> [Concatenate] --> Output
公式:
Output = Concat ( group 1 , group 2 , … , group M ) \text{Output} = \text{Concat}(\text{group}_1, \text{group}_2, \ldots, \text{group}_M) Output=Concat(group1,group2,…,groupM)
group j = Attention ( Q group j , K group j , V group j ) \text{group}_j = \text{Attention}(Q_{\text{group}_j}, K_{\text{group}_j}, V_{\text{group}_j}) groupj=Attention(Qgroupj,Kgroupj,Vgroupj)
4. 多头潜在注意力(MLA)
图示:
Input --> [Compressed Keys & Values]--> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Concatenate] --> Output
公式:
Output = Concat ( head 1 , head 2 , … , head N ) \text{Output} = \text{Concat}(\text{head}_1, \text{head}_2, \ldots, \text{head}_N) Output=Concat(head1,head2,…,headN)
head i = Attention ( Q , K compressed , V compressed ) \text{head}_i = \text{Attention}(Q, K_{\text{compressed}}, V_{\text{compressed}}) headi=Attention(Q,Kcompressed,Vcompressed)
低秩键值联合压缩公式:
K compressed = U K ⋅ S K ⋅ V K T K_{\text{compressed}} = U_K \cdot S_K \cdot V_K^T Kcompressed=UK⋅SK⋅VKT
V compressed = U V ⋅ S V ⋅ V V T V_{\text{compressed}} = U_V \cdot S_V \cdot V_V^T Vcompressed=UV⋅SV⋅VVT
图示概述
- MHA: 每个头独立操作,最终结果拼接。
- MQA: 多个头共享键和值,只计算一次查询,减少计算量。
- GQA: 查询分组,每组共享键和值,进一步减少计算量。
- MLA: 键和值进行压缩,减少内存和计算需求。
这些方法通过不同的策略优化注意力机制,提高了计算效率,降低了内存消耗,使Transformer模型在实际应用中更加高效。
相关文章:

【注意力MHA,MQA,GQA,MLA】
注意力机制优化简明图解 1. 多头注意力(MHA) 图示: Input --> [Attention Head 1]--> [Attention Head 2]--> [Attention Head 3]--> ...--> [Attention Head N]--> [Concatenate] --> Output公式: Outpu…...

《从零开始做个摸鱼小网站! · 序》灵感来源
序 大家好呀,我是summo,这次来写写我在上班空闲(摸鱼)的时候做的一个小网站的事。去年阿里云不是推出了个活动嘛,2核2G的云服务器一年只要99块钱,懂行的人应该知道这个价格在业界已经是非常良心了,虽然优惠只有一年&a…...

计算机基础(Windows 10+Office 2016)教程 —— 第5章 文档编辑软件Word 2016(上)
文档编辑软件Word 2016 5.1 Word 2016入门5.1.1 Word 2016 简介5.1.2 Word 2016 的启动5.1.3 Word 2016 的窗口组成5.1.4 Word 2016 的视图方式5.1.5 Word 2016 的文档操作5.1.6 Word 2016 的退出 5.2 Word 2016的文本编辑5.2.1 输入文本5.2.3 插入与删除文本5.2.4 复制与移动文…...

短视频矩阵管理系统源码:实现短视频内容全面布局
随着移动互联网的普及,短视频应用逐渐成为人们获取信息、娱乐休闲的重要途径。为了满足用户多样化需求,实现短视频内容的全面布局,短视频矩阵管理系统应运而生。本文将详细介绍短视频矩阵管理系统的源码实现,帮助您更好地理解并应…...
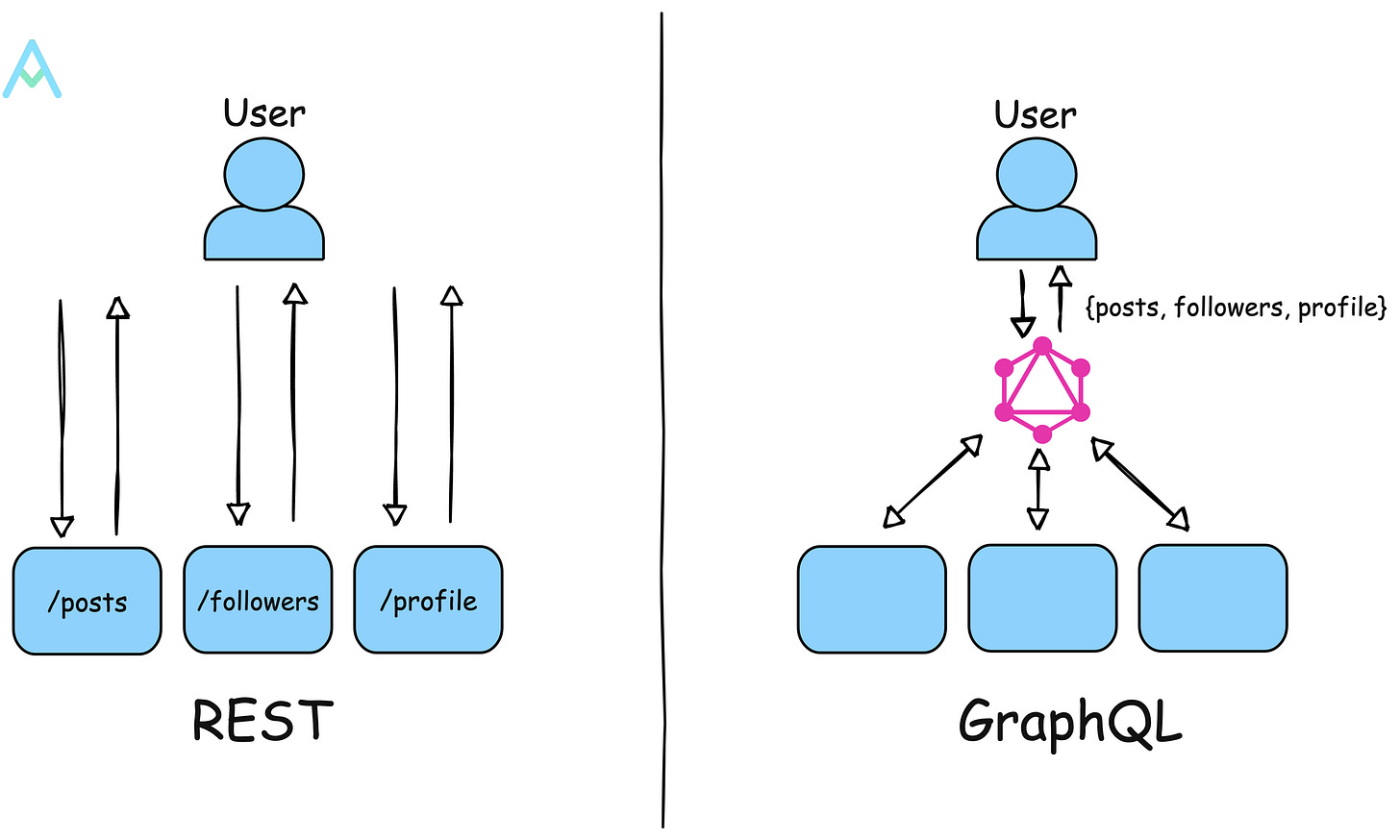
系统设计中15 个最重要的权衡
系统设计的第一法则:一切都与权衡有关。 在设计系统时,我们需要决定要包含哪些功能以及要忽略哪些功能。每次我们做这个决定时,我们都在进行权衡。在本文中,我们将探讨系统设计中遇到的15个最常见的权衡问题,并使用实…...

12年外贸实战经验,一定对你有帮助!
更多外贸干货及开发客户的方法,尽在微信【千千外贸干货】 NO1 客户总是抱怨价格太高,我常以我们产品质量过硬作为回应。但自从我进入贸易公司后,才真正意识到,在商业世界里,价格才是王道。 NO2 如果顾客提出要去工厂检…...
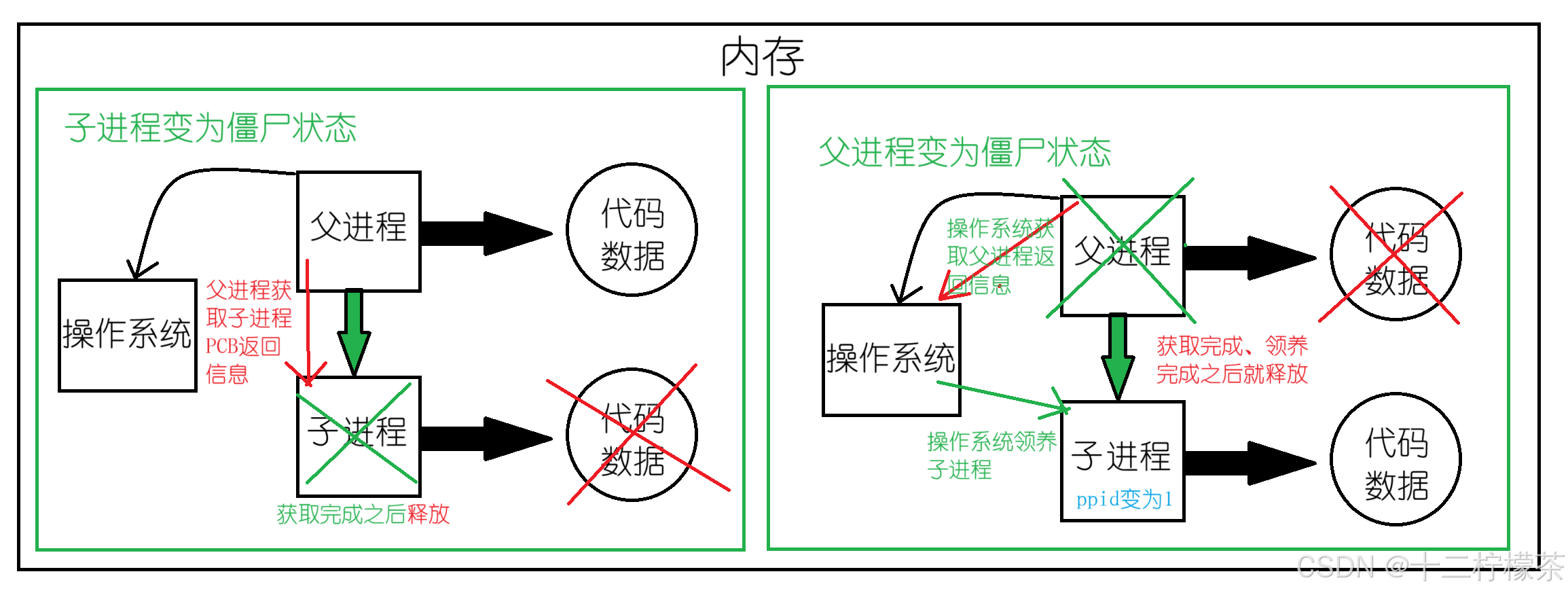
Linux---进程(3)---进程状态
目录 进程排队 进程状态 运行状态 阻塞状态 挂起状态 Linux内核具体进程状态 浅度睡眠状态 运行状态 深度睡眠状态 暂停状态 可被追踪的暂停状态 终止状态 僵尸状态 进程排队 进程不是一直在运行的,进程放在了CPU上,也不是一直运行的。 进程…...

Drools规则引擎实现停车计费
业务规则: 20:00至次日7时不收费白天7:00-20:00每小时5元,每半个小时计费一次进场30分钟内不收费,但计入时间每天最高收费50元 测试项目搭建 pom<?xml version="1.0" encoding="UTF-8"?> <project xmlns="http://maven.apache.org/POM/…...

【python虚拟环境】安装第三方包失败/failed with error code1
问题: 今天新建了一个项目,默认的虚拟环境pip包版本是19.0.3,太低了。安装第三方包的时候一直超时 解决方案: 更新pip: python -m pip install -U --force-reinstall pip然后就可以正常pip install包了 清华镜像源࿱…...

DiffusionModel-latent diffusion,VAE,U-Net,Text-encoder
Diffusers StableDdiffusion 参考: Stable Diffusion原理详解(附代码实现) Latent Diffusion 自编码器(Variational Autoencoder, VAE): 自编码器是一种无监督学习的神经网络,用于学习数据的有效表示或编码。在稳定扩…...
C# form的移植工作
前言: 目标,将一个项目的form移植到新的工程下,且能够正确编译执行: 1 Copy form的两个文件到新工程下: 比如笔者的logo form 2 修改命名空间: 然后,找到新项目的主程序: 的命名…...

linux防火墙相关命令
防火墙启动关闭 启动防火墙 systemctl start firewalld 关闭防火墙 systemctl stop firewalld 查看状态 systemctl status firewalld 开放或限制端口 开放端口 firewall-cmd --zonepublic --add-port22/tcp --permanent 重新载入一下防火墙设置,使设置生效…...

实习中学到的一点计算机知识(MP4在企业微信打不开?)
我在实习中,常有同事向我反馈说我在微信发的视频格式打不开。这就导致我还要一帧帧的盯着某一个时刻来截图,今天查了一下资料尝试修改视频后缀来解决视频的播放问题。 在网上下载mp4的格式,在本地都能播放,怎么可能发上企业微信就…...

ElasticSearch入门语法基础知识
1、创建测试索引 PUT /test_index_person {"settings": {"analysis": {"analyzer": {"ik_analyzer": {"type": "custom","tokenizer": "ik_smart"}}}},"mappings": {"proper…...
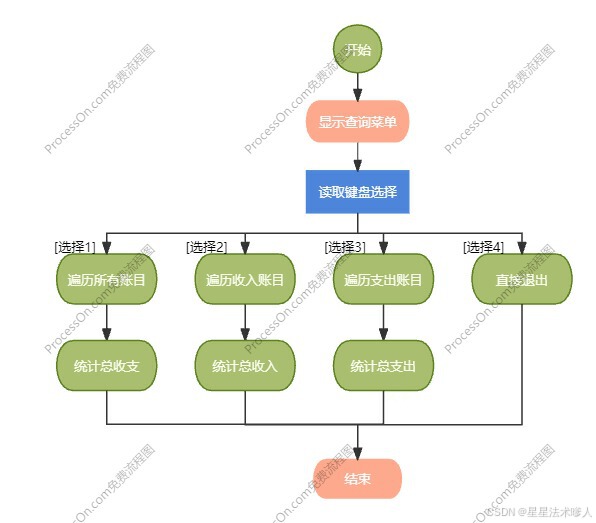
【C++】C++应用案例-dolphin海豚记账本
目录 一、整体介绍 1.1、需求和目标 1.2、整体功能描述 二、页面及功能描述 2.1 主菜单 2.2 记账菜单 2.3 查询菜单 2.4 退出功能 三、流程设计 3.1 主流程 3.2 记账操作流程 3.3 查询操作流程 四、代码设计 4.1 核心思路 4.2 项目文件分类设计 4.2.1 头文件 …...

Matlab数据处理学习笔记
1 :数据清洗 注:数据读取 (1)读取工作表 % 指定要读取的工作表 filename sales_data.xlsx; sheetName Sheet2; % 或者使用工作表编号,例如:sheetNumber 2;% 读取指定工作表的数据 data readtable(fi…...

浏览器中的同源策略、CORS 以及相关的 Fetch API 使用
前言 笔者对前端 Web 技术的认真学习,其实开始于与 Fetch API 的邂逅。当时觉得 fetch() 的设计很不错,也很希望能够请求其它网站下的数据并作处理和展示。学习过程中 HTML 和 CSS 都还好说,由于几乎没有 Web 技术的基础,学习 Fe…...
爬虫 APP 逆向 ---> 粉笔考研
环境: 粉笔考研 v6.3.15:https://www.wandoujia.com/apps/1220941/history_v6031500雷电9 模拟器:https://www.ldmnq.com/安装 magisk:https://blog.csdn.net/Ruaki/article/details/135580772安装 Dia 插件 (作用:禁…...
场 河南大学)
2024河南萌新联赛第(三)场 河南大学
B. 正则表达式 题目: https://ac.nowcoder.com/acm/contest/87865/B 给出n个地址,每个地址的形式为x.x.x.x,找四个x都满足x>0&&x<255的个数 思路: 首先定义四个数组和一个字符,然后按题目所给的形式…...

回溯法---分割回文串
题目:给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。 思路: 第一步:确定参数与返回值。参数为字符串s,分割起始下标startIndex,无返回值 第二…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
