算法刷题笔记 Kruskal算法求最小生成树(详细算法介绍,详细注释C++代码实现)
文章目录
- 题目描述
- 基本思路
- 实现代码
题目描述
- 给定一个
n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数。 - 求最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。
最小生成树的概念:给定一张边带权的无向图G=(V,E),其中V表示图中点的集合,E表示图中边的集合,n=|V|,m=|E|。由V中的全部n个顶点和E中n−1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树。
输入格式
- 第一行包含两个整数
n和m。 - 接下来
m行,每行包含三个整数u,v,w,表示点u和点v之间存在一条权值为w的边。
输出格式
- 共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出
impossible。
数据范围
1 ≤ n ≤ 10^5,1 ≤ m ≤ 2×10^5,- 图中涉及边的边权的绝对值均不超过
1000。
基本思路
- 读题获得的信息:根据该图的点的个数
n和边的条数m的取值范围,可以判定该图是一个稀疏图。 - 算法的基本流程和时间复杂度:
Kruskal算法的基本思路其实非常简单。- 将无向图中的所有边按照权重从小到大进行排序。这一步骤可以使用时间复杂度较低的排序算法,如快速排序。在C++中,我们可以直接利用
<algorithm>头文件中的sort函数来完成排序。值得注意的是,这一步是Kruskal算法的性能瓶颈。当使用快速排序时,其时间复杂度为O(mlogm),其中m是无向图中边的数量。快速排序的常数因子相对于其他同数量级时间复杂度的算法来说较小,因此它具有较好的时间性能,这也使得Kruskal算法在采用快速排序时表现出较高的效率。 - 创建一个空的集合,用于存储最终的边集。接着,遍历无向图中的每一条边。对于每条边,假设其起点编号为
u,终点编号为v,权重为w。如果u和v不在同一个连通分量中,则将该边加入到集合中,并将u和v视为已连通。这里可以使用并查集这种数据结构来高效地实现这一过程。并查集的两个经典操作是:连接两个元素和判断两个元素是否在同一个连通分量中。由于并查集每次操作的时间复杂度为O(α(n)),其中α是阿克曼函数的反函数,其增长非常缓慢,几乎可以认为是常数时间,因此处理所有边的时间复杂度接近O(m)。 - 综上所述,
Kruskal算法的总时间复杂度为O(mlogm + m) = O(mlogm)。
实现代码
#include <cstdio>
#include <algorithm>
using namespace std;// 【辅助结构体定义】无向边结构体
struct undirectedEdge
{int u; // 第一个端点int v; // 第二个端点int w; // 边长(权重)
};
// 【辅助常量定义】记录无向图中点个数的上限
const int N = 100010;// 【变量定义】无向图中点的个数和边的条数
int n, m;
// 【变量定义】每一条无向边的起点编号、终点编号和边长(权重)
int u, v, w;
// 【变量定义】记录无向图中每一条无向边的数组
undirectedEdge graph[2 * N];
// 【变量定义】并查集,记录每一个元素所属的集合编号
int p[N];
// 【变量定义】记录最小生成树的权重之和
int result;
// 【变量定义】记录最小生成树中的边的数量
int edgeCount;// 【辅助函数定义】比较无向边的边长的函数(用于后续无向边边长的升序排序)
inline bool CompareByLength(const undirectedEdge& e1, const undirectedEdge& e2)
{return e1.w < e2.w;
}
// 【辅助函数定义】用于查找和修改指定元素所属的集合编号的函数(用于并查集)
int find(int x)
{return x == p[x] ? x : p[x] = find(p[x]);
}int main(void)
{// 【变量输入】输入点的个数和无向边的条数scanf("%d%d", &n, &m);// 【变量输入】输入每一条无向边的起点编号、终点编号和边长(权重)for(int i = 0; i < m; ++ i){scanf("%d%d%d", &u, &v, &w);// 使用预先定义好的向量来存储无向边graph[i] = {u, v, w};}// 【Krustal算法第一步】依据边长从小到大的顺序对无向边进行排序sort(graph, graph + m, CompareByLength);// 【Krustal算法第二步】从小到大遍历无向边向量,找出所有未连通的边,将边的两个端点合并到一个集合中// 将并查集初始化,让每个元素初始所属的集合编号就是其本身的编号for(int i = 1; i <= n; ++ i) p[i] = i;for(int i = 0; i < m; ++ i){// 首先找到u和v两个端点所属的集合int uRoot = find(graph[i].u), vRoot = find(graph[i].v);// 判定无向边的两个端点是否位于同一个集合中(即是否连通),如果不连通则修改为连通,即加入同一个并查集if(uRoot != vRoot){result += graph[i].w; // 最小生成树权重之和增加++ edgeCount; // 最小生成树边数增加p[uRoot] = vRoot; // 修改两个端点之间的连通性}}// 【Krustal算法第三步】判定是否获得了最小生成树if(edgeCount < n - 1) printf("impossible");else printf("%d", result);return 0;
}
相关文章:
)
算法刷题笔记 Kruskal算法求最小生成树(详细算法介绍,详细注释C++代码实现)
文章目录 题目描述基本思路实现代码 题目描述 给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数。求最小生成树的树边权重之和,如果最小生成树不存在则输出impossible。 最小生成树的概念:给定一张边带权的无向…...

5年经验的软件测试人员,碰到这样的面试题居然会心虚......
我们这边最近的面试机会比较多,但是根据他们的反馈,结束后大部分都没音信了,因为现在企业面试问的非常多,范围非常广,而且开放性的问题很多,很多人即便面试前刷了成百上千道面试题,也很难碰到一…...

C#进阶-轻量级ORM框架Dapper的使用教程与原理详解
本文详细介绍了Dapper在C#中的使用方法,包括Dapper的基本概念、与其他持久层框架的比较、基本语法和高级语法的使用,并通过实例讲解了如何在项目中集成和使用Dapper。Dapper以其高效的性能和简洁的API受到开发者的青睐,适用于各种数据库操作需…...
-MFC-C/C++ - 编辑框(Edit Control) - CEdit)
Windows图形界面(GUI)-MFC-C/C++ - 编辑框(Edit Control) - CEdit
公开视频 -> 链接点击跳转公开课程博客首页 -> 链接点击跳转博客主页 目录 编辑框(Edit Control) - CEdit 基本概念 成员函数 示例代码 编辑框(Edit Control) - CEdit 基本概念 编辑框(Edit Control)是一个允许用户输入和编辑文本的窗…...
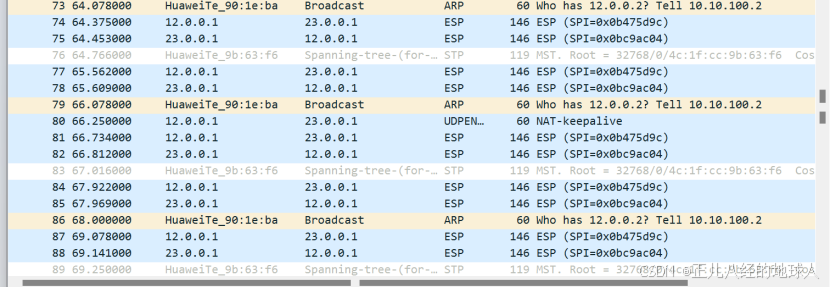
网络安全防御【IPsec VPN搭建】
目录 一、实验拓扑图 二、实验要求 三、实验思路 四、实验步骤: 修改双机热备的为主备模式: 2、配置交换机LSW6新增的配置: 3、防火墙(FW4)做相关的基础配置: 4、搭建IPsec VPN通道 (1…...

java环境配置与tomcat的配置
1、java环境配置 一、JDK下载 访问Oracle官网: 前往Oracle官网(Oracle | Cloud Applications and Cloud Platform),在首页的顶部菜单中选择“Resources” > “Downloads” > “Java” > “JDK”。注意:Orac…...

OD C卷 - 来自异国的客人/幸运数字
来自异国的客人/幸运数字(100) 输入描述: 输入k,n,m k表示物品价值(十进制) k>0 n表示幸运数字, n > 0 m表示异国采用的进制;m > 1 n < m 输出描述: 输出幸运数字的个数࿰…...

C++ | 动态内存管理 new、delete (用法、底层)详解
目录 简单回顾C语言动态内存管理 new、delete的用法 内置类型 new delete 自定义类型 new、delete底层讲解(重要) operator new 与 operator delete 定位 new 结语 简单回顾C语言动态内存管理 在C语言的学习阶段 我们接触到了三个能在堆上开辟…...

【C语言】结构体内存布局解析——字节对齐
🦄个人主页:小米里的大麦-CSDN博客 🎏所属专栏:https://blog.csdn.net/huangcancan666/category_12718530.html 🎁代码托管:黄灿灿 (huang-cancan-xbc) - Gitee.com ⚙️操作环境:Visual Studio 2022 目录 一、引言 二、什么是字节对齐&…...

模型表达方式
目录 一、模型表达概述 二、模型精确表达 2.1 几何表示 (Geometrical Representation) 三、模型非精确表达 3.1 网格表示 (Mesh Representation) 3.2 体素表示 (Voxel Representation) 一、模型表达概述 模型的表达方式多种多样,选择适合的表达方式取决于具体应用场景和…...

校园课程助手【4】-使用Elasticsearch实现课程检索
本节将介绍本项目的查询模块,使用Elasticsearch又不是查询接口,具体流程如图所示(如果不了解Elasticsearch可以使用sql语句进行查询): 这里是两种方法的异同点: Mysql:擅长事务类型操作&#…...

经典运维面试题
1、Linux常见的日志文件都有哪些,各自的用途?日志轮询配置文件在哪里?欢迎界面配置文件在哪里? /var/log/messages #内核及公共消息日志/var/log/cron #计划任务日志/var/log/dmesg #系统引导日志/var/log/malilog #邮件系…...

别再盲目推广了!Xinstall助你开启App线下推广新篇章
在这个数字化飞速发展的时代,App已经成为我们生活中不可或缺的一部分。然而,App市场的竞争也日益激烈,如何让你的App在众多竞争者中脱颖而出,成为每个推广者必须面对的问题。今天,就让我们一起探讨一下App线下推广的痛…...

大厂linux面试题攻略五之数据库管理
一、数据库管理-MySQL语句 0.MySQL基本语句: 1.SQL语句-增 创建xxx用户: mysql>create user xxx % indentified by 123456; xxx表示用户名 %b表示该用户用来连接数据库的方式(远程或本地连接) indentified by 123456设置密码…...

【pytorch】模型集成
在集成学习中,我们会训练多个模型(通常称为「弱学习器」)解决相同的问题,并将它们结合起来以获得更好的结果。最重要的假设是:当弱模型被正确组合时,我们可以得到更精确和/或更鲁棒的模型。 常用的模型集成…...

初识集合和数据结构
目录 初识集合框架数据结构基本概念和术语数据数据元素数据项数据对象前四者的关系数据结构逻辑结构和物理结构逻辑结构物理结构 算法算法设计要求 初识集合框架 Java的集合框架也可被称为容器,是定义在Java.util包下的一些接口和实现类。其就是将多个元素存储到一…...

cocos creator 3.x中动态加载 resources 文件夹下的图片时提示找不到
文件目录如下 类型为spriteFrame 代码案例 图片设置为 sprite-frame、texture 或其他图片类型后,将会在 资源管理器 中生成一个对应类型的资源。但如果直接加载 equipments/testea,得到的类型将会是 ImageAsset,必须指定路径到具体的子资源…...

第九十八周周报
学习时间: 2024.7.27-204.8.3 学习产出: 这周主要在按照审稿人的意见修改论文,由于有个模型保存的文件找不到了,所以重新训练花了点时间,目前已经把修改后的论文和cover letter发给杨老师了。...

程序员找工作之数据结构面试题总结分析
文章目录 1. 数据结构的基本概念与分类2. 数据结构的存储与表示3. 数据元素的存储与关系4. 存储结构的选择与考量5. 特定数据结构的定义与特性6. 数据结构操作与应用7. 数组与存储8. 特定数据结构的存储与访问 程序员在找工作面试中,数据结构方面可能会被问到的问题…...

设置provider解决maven找不到JUnit 5测试样例
问题描述 尝试复现一个用大模型生成测试样例的工作,但使用maven生成的JUnit 5测试样例死活不执行。又不想用命令行运行,因此进行排查 基本知识 <dependencies> junit-jupiter-api JUnit 5写代码时调用的库 junit-jupyter-engine 运行JUnit 5测…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
