当前位置： 首页 > news >正文

机器学习练手（三）：基于决策树的iris 多分类和波士顿房价预测

news 2025/12/7 0:12:21

总结：本文为和鲸python 可视化探索训练营资料整理而来，加入了自己的理解（by GPT4o）

原活动链接

原作者：vgbhfive，多年风控引擎研发及金融模型开发经验，现任某公司风控研发工程师，对数据分析、金融模型开发、风控引擎研发具有丰富经验。

在前一关中学习了如何使用肘部法则计算最佳分类数，也知道了计算 KMeans 分类的特征要求。在新的一关中，我们将开始学习训练决策树模型。

总结：注意训练模型后打印特征重要性的操作，clf.feature_importances_ ，用于后续优化模型

目录

      • 决策树
      • iris 数据集之多分类问题
        • 引入依赖
        • 加载数据
        • 训练模型和计算测试集指标
        • 特征重要性
        • 可视化决策树
        • 总结
      • 波士顿房价之回归问题
        • 加载数据
        • 预处理数据
        • 训练回归模型
        • 计算测试集指标
      • 闯关题
        • STEP1：请根据要求完成题目

决策树

决策树字如其名，其主要展示类似于树状结构。

在分类问题中，表示基于特征对实例进行分类的过程，过程可以认为是 if-then 的集合 ;而在回归问题中，会被认为特征分布在分类空间上的条件概率分布。

iris 数据集之多分类问题

Iris 数据集算是机器学习算法的入门数据集，其包含有三个分类结果和四个特征信息，其分别是花萼长度，花萼宽度，花瓣长度，花瓣宽度，通过上述四个特征信息预测鸢尾花卉属于哪一类？

引入依赖
import pandas as pd
import numpy as npfrom sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
from sklearn.metrics import accuracy_score, r2_score, mean_squared_error
加载数据
# 1. 加载数据iris = load_iris()
x, y = pd.DataFrame(iris.data), iris.target
x.head(), y

(     0    1    2    30  5.1  3.5  1.4  0.21  4.9  3.0  1.4  0.22  4.7  3.2  1.3  0.23  4.6  3.1  1.5  0.24  5.0  3.6  1.4  0.2,array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]))
训练模型和计算测试集指标
# 2. 切分数据集x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3,random_state=42)
x_train, x_test, y_train, y_test

(       0    1    2    381   5.5  2.4  3.7  1.0133  6.3  2.8  5.1  1.5137  6.4  3.1  5.5  1.875   6.6  3.0  4.4  1.4109  7.2  3.6  6.1  2.5..   ...  ...  ...  ...71   6.1  2.8  4.0  1.3106  4.9  2.5  4.5  1.714   5.8  4.0  1.2  0.292   5.8  2.6  4.0  1.2102  7.1  3.0  5.9  2.1[105 rows x 4 columns],0    1    2    373   6.1  2.8  4.7  1.218   5.7  3.8  1.7  0.3118  7.7  2.6  6.9  2.378   6.0  2.9  4.5  1.576   6.8  2.8  4.8  1.431   5.4  3.4  1.5  0.464   5.6  2.9  3.6  1.3141  6.9  3.1  5.1  2.368   6.2  2.2  4.5  1.582   5.8  2.7  3.9  1.2110  6.5  3.2  5.1  2.012   4.8  3.0  1.4  0.136   5.5  3.5  1.3  0.29    4.9  3.1  1.5  0.119   5.1  3.8  1.5  0.356   6.3  3.3  4.7  1.6104  6.5  3.0  5.8  2.269   5.6  2.5  3.9  1.155   5.7  2.8  4.5  1.3132  6.4  2.8  5.6  2.229   4.7  3.2  1.6  0.2127  6.1  3.0  4.9  1.826   5.0  3.4  1.6  0.4128  6.4  2.8  5.6  2.1131  7.9  3.8  6.4  2.0145  6.7  3.0  5.2  2.3108  6.7  2.5  5.8  1.8143  6.8  3.2  5.9  2.345   4.8  3.0  1.4  0.330   4.8  3.1  1.6  0.222   4.6  3.6  1.0  0.215   5.7  4.4  1.5  0.465   6.7  3.1  4.4  1.411   4.8  3.4  1.6  0.242   4.4  3.2  1.3  0.2146  6.3  2.5  5.0  1.951   6.4  3.2  4.5  1.527   5.2  3.5  1.5  0.24    5.0  3.6  1.4  0.232   5.2  4.1  1.5  0.1142  5.8  2.7  5.1  1.985   6.0  3.4  4.5  1.686   6.7  3.1  4.7  1.516   5.4  3.9  1.3  0.410   5.4  3.7  1.5  0.2,array([1, 2, 2, 1, 2, 1, 2, 1, 0, 2, 1, 0, 0, 0, 1, 2, 0, 0, 0, 1, 0, 1,2, 0, 1, 2, 0, 2, 2, 1, 1, 2, 1, 0, 1, 2, 0, 0, 1, 1, 0, 2, 0, 0,1, 1, 2, 1, 2, 2, 1, 0, 0, 2, 2, 0, 0, 0, 1, 2, 0, 2, 2, 0, 1, 1,2, 1, 2, 0, 2, 1, 2, 1, 1, 1, 0, 1, 1, 0, 1, 2, 2, 0, 1, 2, 2, 0,2, 0, 1, 2, 2, 1, 2, 1, 1, 2, 2, 0, 1, 2, 0, 1, 2]),array([1, 0, 2, 1, 1, 0, 1, 2, 1, 1, 2, 0, 0, 0, 0, 1, 2, 1, 1, 2, 0, 2,0, 2, 2, 2, 2, 2, 0, 0, 0, 0, 1, 0, 0, 2, 1, 0, 0, 0, 2, 1, 1, 0,0]))

# 3. 构建决策树模型并训练模型clf = DecisionTreeClassifier(criterion='gini')clf.fit(x_train, y_train)

DecisionTreeClassifier()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. 
DecisionTreeClassifier()
# 4. 预测测试集y_pred = clf.predict(x_test)

# 5. 计算测试集的准确率acc = accuracy_score(y_test, y_pred)
acc

1.0
特征重要性
# 6. 特征重要性
# feature_importances_ 是一个数组类型，里边的元素分别代表对应特征的重要性，所有元素之和为1。元素的值越大，则对应的特征越重要。imprtances = clf.feature_importances_
imprtances

array([0.        , 0.01911002, 0.42356658, 0.5573234 ])
可视化决策树
# 打印决策树from sklearn.tree import export_graphviz
import graphviz# clf 为决策树对象
dot_data = export_graphviz(clf)
graph = graphviz.Source(dot_data)# 生成 Source.gv.pdf 文件，可以下载打开
# graph.view()

Image Name

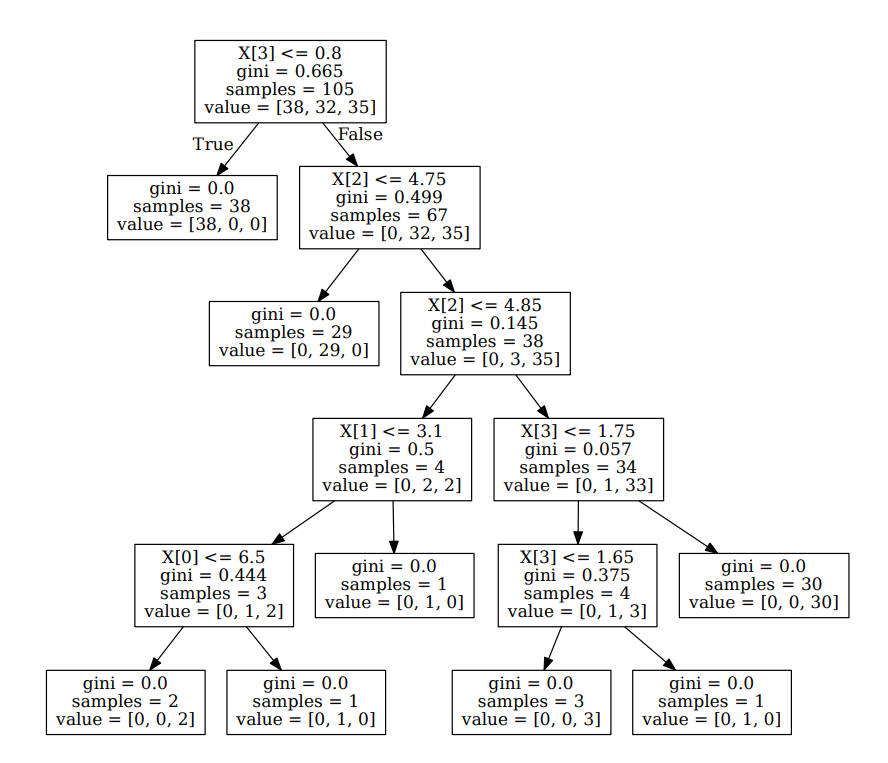
总结

通过可视化决策树，可以看出正如前面介绍的那样，分类决策树是 if-then 的集合，最终得到对应的分类结果。

波士顿房价之回归问题

在二手房产交易中，其中最受关注的便是房屋价格问题，其涉及到多个方方面面，例如房屋面积、房屋位置、户型大小、户型面积、小区平均房屋价格等等信息。现在 sklearn 提供波士顿的房屋价格数据集，其中有 506 例记录，包含城镇人均犯罪率、住宅用地比例、平均房间数等特征信息，学习使用这些信息准确预测波士顿的房屋价格，之后以此类推收集想要购买区域的房屋价格信息，就可以预测自身购买房屋价格是否划算。

波士顿房价数据集数据含义如下：

特征列名称特征含义
CRIM城镇人均犯罪率
ZN占地面积超过25,000平方英尺的住宅用地比例
INDUS每个城镇非零售业务的比例
CHASCharles River虚拟变量
NOX一氧化氮浓度（每千万份）
RM每间住宅的平均房间数
AGE1940年以前建造的自住单位比例
DIS波士顿的五个就业中心加权距离
RAD径向高速公路的可达性指数
TAX每10,000美元的全额物业税率
PTRATIO城镇的学生与教师比例
B1000*(Bk / 0.63)^2 其中Bk是城镇黑人的比例
LSTAT区域中被认为是低收入阶层的比率
MEDV自有住房的中位数报价, 单位1000美元
加载数据
# 1. 加载数据boston = pd.read_csv('./data/housing-3.csv')
boston.head()
CRIMZNINDUSCHASNOXRMAGEDISRADTAXPIRATIOBLSTATMEDV
00.0063218.02.3100.5386.57565.24.09001296.015.3396.904.9824.0
10.027310.07.0700.4696.42178.94.96712242.017.8396.909.1421.6
20.027290.07.0700.4697.18561.14.96712242.017.8392.834.0334.7
30.032370.02.1800.4586.99845.86.06223222.018.7394.632.9433.4
40.069050.02.1800.4587.14754.26.06223222.018.7396.905.3336.2
预处理数据
# 2. 获取特征集和房价
x = boston.drop(['MEDV'], axis=1)
y = boston['MEDV']
x.head(), y.head()

(      CRIM    ZN  INDUS  CHAS    NOX     RM   AGE     DIS  RAD    TAX  \0  0.00632  18.0   2.31     0  0.538  6.575  65.2  4.0900    1  296.0   1  0.02731   0.0   7.07     0  0.469  6.421  78.9  4.9671    2  242.0   2  0.02729   0.0   7.07     0  0.469  7.185  61.1  4.9671    2  242.0   3  0.03237   0.0   2.18     0  0.458  6.998  45.8  6.0622    3  222.0   4  0.06905   0.0   2.18     0  0.458  7.147  54.2  6.0622    3  222.0   PIRATIO       B  LSTAT  0     15.3  396.90   4.98  1     17.8  396.90   9.14  2     17.8  392.83   4.03  3     18.7  394.63   2.94  4     18.7  396.90   5.33  ,0    24.01    21.62    34.73    33.44    36.2Name: MEDV, dtype: float64)

# 3. 测试集与训练集 7:3x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.33)
x_train.head(), x_test.head(), y_train.head(), y_test.head()

(         CRIM    ZN  INDUS  CHAS    NOX     RM    AGE     DIS  RAD    TAX  \492   0.11132   0.0  27.74     0  0.609  5.983   83.5  2.1099    4  711.0   266   0.78570  20.0   3.97     0  0.647  7.014   84.6  2.1329    5  264.0   91    0.03932   0.0   3.41     0  0.489  6.405   73.9  3.0921    2  270.0   379  17.86670   0.0  18.10     0  0.671  6.223  100.0  1.3861   24  666.0   89    0.05302   0.0   3.41     0  0.489  7.079   63.1  3.4145    2  270.0   PIRATIO       B  LSTAT  492     20.1  396.90  13.35  266     13.0  384.07  14.79  91      17.8  393.55   8.20  379     20.2  393.74  21.78  89      17.8  396.06   5.70  ,CRIM    ZN  INDUS  CHAS    NOX     RM   AGE     DIS  RAD    TAX  \399  9.91655   0.0  18.10     0  0.693  5.852  77.8  1.5004   24  666.0   305  0.05479  33.0   2.18     0  0.472  6.616  58.1  3.3700    7  222.0   131  1.19294   0.0  21.89     0  0.624  6.326  97.7  2.2710    4  437.0   452  5.09017   0.0  18.10     0  0.713  6.297  91.8  2.3682   24  666.0   121  0.07165   0.0  25.65     0  0.581  6.004  84.1  2.1974    2  188.0   PIRATIO       B  LSTAT  399     20.2  338.16  29.97  305     18.4  393.36   8.93  131     21.2  396.90  12.26  452     20.2  385.09  17.27  121     19.1  377.67  14.27  ,492    20.1266    30.791     22.0379    10.289     28.7Name: MEDV, dtype: float64,399     6.3305    28.4131    19.6452    16.1121    20.3Name: MEDV, dtype: float64)
训练回归模型
# 4. 创建 CART 回归树dtr = DecisionTreeRegressor()

# 5. 训练构造 CART 回归树dtr.fit(x_train, y_train)

DecisionTreeRegressor()
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org. 
DecisionTreeRegressor()
# 6. 预测测试集中的房价y_pred = dtr.predict(x_test)
y_pred

array([ 7.5, 28.7, 19.2, 16.7, 22. , 26.6, 21. , 15. , 13.2, 23.2,  8.8,25. , 13.8, 30.7, 32. , 13.3, 22.9, 19.6, 22.7,  8.8, 19.9, 15.6,7.5, 11.7, 36.2, 28.1, 17. , 20.2, 14.9, 25. , 20.2, 27.1, 17.5,36. , 14.9,  9.5, 23. , 16.7, 24.8, 20. , 20. ,  8.3, 31.6, 14.1,23.7, 19.4, 33.4, 29.6, 14.1, 22. , 23.1, 50. , 50. ,  8.3, 11.8,21. , 27.5, 15.2, 20. , 18.3,  8.3, 20.1, 17.6, 18.5, 32. , 17. ,19.9, 18.8, 11.7, 25. , 16. , 26.4, 32.7, 20.6, 50. , 14.4, 34.6,11.8, 20.1, 22.4, 28.6, 36.4, 12.6, 19.8, 34.6, 22.9,  5. , 33.1,50. , 20.3, 26.7, 18.2, 28.1, 44.8, 50. , 16. , 26.4, 23.2, 22.2,12. ,  8.3, 18.2, 19.6, 21.6, 11.9, 18.3, 28.1, 24.7, 22. , 32.5,20.6, 16.6, 18.2, 14.1, 20.5, 22. , 22.9,  7.5, 16.6, 19.9, 18.7,27.9, 23.2, 17.2, 23.8, 22.2, 20.9, 13.6, 19.3,  9.5, 27.9,  7.5,34.6, 13.8,  8.3, 50. , 10.2, 12.6, 32. , 24.2, 17. , 19.5, 23.7,24.3, 13.6, 22.6,  8.3, 23.1, 21.6, 24.5, 14. , 23.3, 24.4, 16.6,14.9, 22. ,  8.3, 19.9, 12.6, 10.2, 23.4, 24.7, 50. , 19.4, 20. ,14.3, 23. ])
计算测试集指标
# 7. 测试集结果评价
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error# r2_score 决定系数，反映因变量的全部变异能通过回归关系被自变量解释的比例。
r2 = r2_score(y_test, y_pred)
mse = mean_squared_error(y_test, y_pred)
# 计算均值绝对误差 (MAE)
mae = mean_absolute_error(y_test, y_pred)
r2, mse, mae

(0.6862919611706397, 22.763832335329337, 3.143712574850299)

闯关题

STEP1：请根据要求完成题目

Q1. iris数据集中共有四个特征，重要性最小的特征是哪个？
A. 花萼长度
B. 花萼宽度
C. 花瓣长度
D. 花瓣宽度

a1 = 'A'

# 获取数据集描述
print(iris.DESCR)

.. _iris_dataset:Iris plants dataset
--------------------**Data Set Characteristics:**:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:- sepal length in cm- sepal width in cm- petal length in cm- petal width in cm- class:- Iris-Setosa- Iris-Versicolour- Iris-Virginica:Summary Statistics:============== ==== ==== ======= ===== ====================Min  Max   Mean    SD   Class Correlation
============== ==== ==== ======= ===== ====================
sepal length:   4.3  7.9   5.84   0.83    0.7826
sepal width:    2.0  4.4   3.05   0.43   -0.4194
petal length:   1.0  6.9   3.76   1.76    0.9490  (high!)
petal width:    0.1  2.5   1.20   0.76    0.9565  (high!)
============== ==== ==== ======= ===== ====================:Missing Attribute Values: None
:Class Distribution: 33.3% for each of 3 classes.
:Creator: R.A. Fisher
:Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov)
:Date: July, 1988The famous Iris database, first used by Sir R.A. Fisher. The dataset is taken
from Fisher's paper. Note that it's the same as in R, but not as in the UCI
Machine Learning Repository, which has two wrong data points.This is perhaps the best known database to be found in the
pattern recognition literature.  Fisher's paper is a classic in the field and
is referenced frequently to this day.  (See Duda & Hart, for example.)  The
data set contains 3 classes of 50 instances each, where each class refers to a
type of iris plant.  One class is linearly separable from the other 2; the
latter are NOT linearly separable from each other... dropdown:: References- Fisher, R.A. "The use of multiple measurements in taxonomic problems"Annual Eugenics, 7, Part II, 179-188 (1936); also in "Contributions toMathematical Statistics" (John Wiley, NY, 1950).- Duda, R.O., & Hart, P.E. (1973) Pattern Classification and Scene Analysis.(Q327.D83) John Wiley & Sons.  ISBN 0-471-22361-1.  See page 218.- Dasarathy, B.V. (1980) "Nosing Around the Neighborhood: A New SystemStructure and Classification Rule for Recognition in Partially ExposedEnvironments".  IEEE Transactions on Pattern Analysis and MachineIntelligence, Vol. PAMI-2, No. 1, 67-71.- Gates, G.W. (1972) "The Reduced Nearest Neighbor Rule".  IEEE Transactionson Information Theory, May 1972, 431-433.- See also: 1988 MLC Proceedings, 54-64.  Cheeseman et al"s AUTOCLASS IIconceptual clustering system finds 3 classes in the data.- Many, many more ...

​

相关文章：

机器学习练手（三）：基于决策树的iris 多分类和波士顿房价预测

总结：本文为和鲸python 可视化探索训练营资料整理而来，加入了自己的理解（by GPT4o） 原活动链接 原作者：vgbhfive，多年风控引擎研发及金融模型开发经验，现任某公司风控研发工程师，对…...

编程日记 2024/8/4 5:05:57

PS 2024 百种常用插件下载安装教程【免费使用，先到先得】

文章目录 软件介绍软件下载安装步骤 专栏推荐： 超多精品软件（持续更新中…） 软件推荐： PS 2024 PR 2024 软件介绍 PS常用插件 此软件整合了市面近百款ps处理插件，可实现：一键制作背景，一键抠图…...

编程日记 2024/8/4 5:04:56

逻辑推理之lora微调

逻辑推理微调 比赛介绍准备内容lora微调lora微调介绍lora优势代码内容 start_vllm相关介绍调用 运行主函数提交结果总结相应连接 比赛介绍 本比赛旨在测试参与者的逻辑推理和问题解决能力。参与者将面对一系列复杂的逻辑谜题，涵盖多个领域的推理挑战。 比赛的连接:…...

编程日记 2024/8/4 5:03:54

前端-防抖代码

//防抖debounce(fn, time 1000) {let timer null;return function (...args) {if (timer) clearTimeout(timer);timer setTimeout(() > {fn.apply(this, args);}, time);};},// 输入变化处理函数async inputChange(value) {if (!this.debouncedInputChange) {this.deboun…...

编程日记 2024/8/4 5:02:53

langchain 入门指南 - 让 LLM 自动选择不同的 Prompt

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。 让 LLM 自动选择不同的 Prompt 在上一篇文章中，我们学会了如何让 langchain 来自动选择不同的 LLM Chain，以便回…...

编程日记 2024/8/4 5:01:52

web浏览器播放rtsp视频流，海康监控API

概述 这里记录一下如何让前端播放rtsp协议的视频流 ​ 项目中调用海康API，生成的视频流(hls、ws、rtmp等)通过PotPlayer播放器都无法播放，说明视频流有问题，唯独rtsp视频流可以播放。 但是浏览器本身是无法播放rtsp视频的，即使…...

编程日记 2024/8/4 5:00:51

操作系统原理：程序、进程、线程的概念

文章目录 程序、进程、线程的概念程序（Program）进程（Process）线程（Thread）关系总结 在日常对操作系统的使用中，大家肯定对程序、进程和线程多少有所耳闻。作为操作系统的重要一部分，…...

编程日记 2024/8/4 4:59:48

Golang是如何实现动态数组功能的?Slice切片原理解析

Hi 亲爱的朋友们，我是 k 哥。今天，咱们聊一聊Golang 切片。 当我们需要使用数组，但是又不能提前定义数组大小时，可以使用golang的动态数组结构，slice切片。在 Go 语言的众多特性里，slice 是我们经常用到的数…...

编程日记 2024/8/4 4:58:48

SQL注入 报错注入+附加拓展知识，一篇文章带你轻松入门

第5关--------------------------------------------> 前端直接不会显示账号密码的打印；但是在接收前端的数据的那部分后端那里，会看前端传递过来的值是否正确，如果不正确，后端接收值那里就会当MySQL语句执行错误，…...

编程日记 2024/8/4 4:57:44

springboot项目里的包spring-boot-dependencies依赖介绍

springboot项目里的包’spring-boot-dependencies‘依赖 我们一般是在项目的pom dependencyManagement标签里引入spring-boot-dependencies，或者根spring-boot-starter-parent里也是继承了它,也正是因为继承了这个依赖，所以我们在写依赖时才不需要写版本…...

编程日记 2024/8/4 4:56:43

C# 下的限定符运算详解（全部，任意，包含）与示例

文章目录 1.限定符概述2. 全部限定符运算（All）3. 任意限定符运算（Any）4. 包含限定符运算（Contains）总结 当我们在C#编程中需要进行条件判断或集合操作时，限定符（qualifiers&#xff…...

编程日记 2024/8/4 4:54:41

消息队列RabbitMQ部分知识

1.简述RabbitMQ的架构设计 RabbitMQ 是一个开源的消息代理，采用了高级消息队列协议（AMQP），其架构设计主要包括以下几个关键组件和概念： 1.消息生产者（ Producer）： 负责发送消息到…...

编程日记 2024/8/4 4:53:40

看门狗应用编程-I.MX6U嵌入式Linux C应用编程学习笔记基于正点原子阿尔法开发板

看门狗应用编程 看门狗应用编程介绍 看门狗定时器的基本概念 看门狗是一个可以在一定时间内被复位/重置的计数器 如果在规定时间内没有复位，看门狗计时器溢出会对CPU产生复位信号使系统重启 有些看门狗可以只产生中断信号而不会使系统复位 I.MX6UL/I.MX6ULL So…...

编程日记 2024/8/4 4:52:39

Bug 解决 | 本地项目上线后出现错误

目录 一、前言 二、原因分析 1、本地代码误发线上 2、环境差异 3、配置差异 4、资源路径差异 5、API 接口差异 6、用量差异 一、前言 大家好，我是小洪爱分享。在开发上线项目的过程中，我们经常会遇到一种让人头疼的情况。那就是开发好的项目功能…...

编程日记 2024/8/4 4:51:37

为什么我工作 10 年后转行当程序员？逆袭翻盘！

今天文章的主人公暂且称他为 A 君。不过 A 君有点特别，非科班，工作 10 年后才转行 iOS 程序员。今年 36 岁，目前在某行业头部企业任职前端负责人，管理 40 人的前端团队。 废话不多说，我们开始 A 君（为了描…...

编程日记 2024/8/4 4:50:35

见证中国数据库的崛起：从追赶到引领的壮丽征程《四》

见证中国数据库的崛起：从追赶到引领的壮丽征程《四》 四、未来展望：中国数据库的机遇与挑战新技术带来的机遇全球化竞争的挑战数据安全与隐私保护的挑战人才培养的持续挑战 【纪录片】中国数据库前世今生 在数字化潮流席卷全球的今天，数据库作…...

编程日记 2024/8/4 4:49:34

OpenCV||超细节的基本操作

一、图像读取 retval cv2.imread(filename[, flags]) filename：需要读取的图片路径名，支持多种图片格式，如JPEG、PNG、TIFF等。flags：一个可选参数，指定加载图像的颜色类型。常用的值包括： cv2.IMGEAD_A…...

编程日记 2024/8/4 4:48:33

算法训练（leetcode）第三十八天 | 1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和、392. 判断子序列

刷题记录 *1143. 最长公共子序列1035. 不相交的线53. 最大子数组和392. 判断子序列 *1143. 最长公共子序列 leetcode题目地址 本题和718. 最长重复子数组相似，只是本题不要求连续，需要记录前面最长的子序列，在此基础上累计长度。 dp[i][j]…...

编程日记 2024/8/4 4:47:32

STM32——外部中断（EXTI）

目录 前言 一、外部中断基础知识 二、使用步骤 三、固件库实现 四、STM32CubeMX实现 总结 前言 外部中断（External Interrupt，简称EXTI）是微控制器用于响应外部事件的一种方式，当外部事件发生时（如按键按下、传感器信号…...

编程日记 2024/8/4 4:46:31

MySQL多实例部署

1、软件包下载 //环境：一台rocky Linux虚拟机，并且做好的基本配置及时钟同步，使用Xshell连接 [rootmysql ~]# yum -y install tar lrzsz libncurses* libaio perl//将包文件拖进去 [rootmysql ~]# rz -E rz waiting to receive. [rootmysql…...

编程日记 2024/8/4 4:44:28

SkyWalking 10.2.0 SWCK 配置过程

SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外，K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案，全安装在K8S群集中。 具体可参…...

编程新知 2025/8/23 5:51:08

stm32G473的flash模式是单bank还是双bank？

今天突然有人stm32G473的flash模式是单bank还是双bank？由于时间太久，我真忘记了。搜搜发现，还真有人和我一样。见下面的链接：https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

编程新知 2025/12/5 22:36:45

51c自动驾驶~合集58

我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留，CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制（CCA-Attention），…...

编程新知 2025/12/2 6:11:19

PHP和Node.js哪个更爽?

先说结论，rust完胜。 php：laravel，swoole，webman，最开始在苏宁的时候写了几年php，当时觉得php真的是世界上最好的语言，因为当初活在舒适圈里，不愿意跳出来，就好比当初活在…...

编程新知 2025/9/14 7:59:52

Admin.Net中的消息通信SignalR解释

定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

编程新知 2025/9/10 5:36:56

关于nvm与node.js

1 安装nvm 安装过程中手动修改 nvm的安装路径， 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解，但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后，通常在该文件中会出现以下配置&…...

编程新知 2025/12/3 23:11:03

CentOS下的分布式内存计算Spark环境部署

一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架，相比 MapReduce 具有以下核心优势： 内存计算：数据可常驻内存，迭代计算性能提升 10-100 倍（文档段落：3-79…...

编程新知 2025/12/4 21:05:06

服务器硬防的应用场景都有哪些？

服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式，避免服务器受到各种恶意攻击和网络威胁，那么，服务器硬防通常都会应用在哪些场景当中呢？ 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

编程新知 2025/11/9 19:17:07

定时器任务——若依源码分析

分析util包下面的工具类schedule utils： ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类，封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz，先构建任务的 JobD…...

编程新知 2025/12/4 22:44:51

在四层代理中还原真实客户端ngx_stream_realip_module

一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡（如 HAProxy、AWS NLB、阿里 SLB）发起上游连接时，将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后，ngx_stream_realip_module 从中提取原始信息…...

编程新知 2025/11/18 8:33:43