最短路径算法:Floyd-Warshall算法
引言
在图论中,Floyd-Warshall算法是一种用于计算任意两点之间最短路径的动态规划算法。它适用于加权有向图和无向图,可以处理带有负权重边的图,但要求图中不能有负权重环。本文将详细介绍Floyd-Warshall算法的定义、步骤及其实现。
Floyd-Warshall算法
定义
Floyd-Warshall算法是一种用于计算图中所有顶点对之间最短路径的算法。该算法利用动态规划的思想,通过不断更新顶点对之间的最短路径,最终得到所有顶点对的最短路径矩阵。
算法步骤
- 初始化:创建一个距离矩阵dist,其中dist[i][j]表示顶点i到顶点j的初始距离。如果i和j之间有边,则dist[i][j]为边的权重;如果i和j之间没有边且i≠j,则dist[i][j]为正无穷大;如果i=j,则dist[i][j]为0。
- 更新距离矩阵:对于每一对顶点(i, j),通过中间顶点k更新其最短路径。具体来说,如果dist[i][j] > dist[i][k] + dist[k][j],则更新dist[i][j] = dist[i][k] + dist[k][j]。
- 重复更新:重复上述步骤,直到所有顶点对之间的最短路径都被计算出来。
示例
假设我们有一个带权有向图,顶点集合为 ({A, B, C, D}),边和权重集合为 ({(A, B, 3), (A, C, 8), (A, D, -4), (B, D, 1), (B, C, -2), (C, A, 4), (D, C, 7), (D, B, -5)})。
Floyd-Warshall算法图解
- 初始化距离矩阵:
A B C D
A 0 3 8 -4
B ∞ 0 -2 1
C 4 ∞ 0 ∞
D ∞ -5 7 0
- 通过顶点A更新距离矩阵:
A B C D
A 0 3 8 -4
B 7 0 -2 1
C 4 ∞ 0 ∞
D 3 -5 7 0
- 通过顶点B更新距离矩阵:
A B C D
A 0 3 1 -4
B 5 0 -2 1
C 4 7 0 ∞
D 3 -5 2 0
- 通过顶点C更新距离矩阵:
A B C D
A 0 3 1 -4
B 5 0 -2 1
C 4 7 0 ∞
D 3 -5 2 0
- 通过顶点D更新距离矩阵:
A B C D
A 0 -1 1 -4
B 5 0 -2 1
C 4 -1 0 -3
D 3 -5 2 0
Floyd-Warshall算法实现
下面是用Java实现Floyd-Warshall算法的代码示例:
import java.util.Arrays;public class FloydWarshallAlgorithm {private static final int INF = 99999; // 表示无穷大的值// 计算任意两点之间的最短路径public void floydWarshall(int[][] graph) {int vertices = graph.length;int[][] dist = new int[vertices][vertices];// 初始化距离矩阵for (int i = 0; i < vertices; i++) {for (int j = 0; j < vertices; j++) {dist[i][j] = graph[i][j];}}// 更新距离矩阵for (int k = 0; k < vertices; k++) {for (int i = 0; i < vertices; i++) {for (int j = 0; j < vertices; j++) {if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];}}}}printSolution(dist);}// 打印最短路径矩阵private void printSolution(int[][] dist) {int vertices = dist.length;System.out.println("顶点对之间的最短路径矩阵:");for (int i = 0; i < vertices; i++) {for (int j = 0; j < vertices; j++) {if (dist[i][j] == INF) {System.out.print("INF ");} else {System.out.print(dist[i][j] + " ");}}System.out.println();}}public static void main(String[] args) {int[][] graph = {{0, 3, 8, -4},{INF, 0, -2, 1},{4, INF, 0, INF},{INF, -5, 7, 0}};FloydWarshallAlgorithm floydWarshall = new FloydWarshallAlgorithm();floydWarshall.floydWarshall(graph);}
}
代码注释
-
常量定义:
private static final int INF = 99999; // 表示无穷大的值INF表示无穷大,用于表示顶点之间没有直接连接。 -
Floyd-Warshall算法:
public void floydWarshall(int[][] graph) {int vertices = graph.length;int[][] dist = new int[vertices][vertices];// 初始化距离矩阵for (int i = 0; i < vertices; i++) {for (int j = 0; j < vertices; j++) {dist[i][j] = graph[i][j];}}// 更新距离矩阵for (int k = 0; k < vertices; k++) {for (int i = 0; i < vertices; i++) {for (int j = 0; j < vertices; j++) {if (dist[i][k] != INF && dist[k][j] != INF && dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];}}}}printSolution(dist); }floydWarshall方法实现了Floyd-Warshall算法,计算任意两点之间的最短路径。 -
打印最短路径矩阵:
private void printSolution(int[][] dist) {int vertices = dist.length;System.out.println("顶点对之间的最短路径矩阵:");for (int i = 0; i < vertices; i++) {for (int j = 0; j < vertices; j++) {if (dist[i][j] == INF) {System.out.print("INF ");} else {System.out.print(dist[i][j] + " ");}}System.out.println();} }printSolution方法用于打印最短路径矩阵。
结论
通过上述讲解和实例代码,我们详细展示了Floyd-Warshall算法的定义、步骤及其实现。Floyd-Warshall算法是一种重要的最短路径算法,适用于计算任意两点之间的最短路径。希望这篇博客对您有所帮助!
如果您觉得这篇文章对您有帮助,请关注我的CSDN博客,点赞并收藏这篇文章,您的支持是我持续创作的动力!
关键内容总结:
- Floyd-Warshall算法的定义
- Floyd-Warshall算法的步骤
- Floyd-Warshall算法的实现及其
代码注释
推荐阅读:深入探索设计模式专栏,详细讲解各种设计模式的应用和优化。点击查看:深入探索设计模式。
特别推荐:设计模式实战专栏,深入解析设计模式的实际应用,提升您的编程技巧。点击查看:设计模式实战。
如有任何疑问或建议,欢迎在评论区留言讨论。谢谢阅读!
相关文章:

最短路径算法:Floyd-Warshall算法
引言 在图论中,Floyd-Warshall算法是一种用于计算任意两点之间最短路径的动态规划算法。它适用于加权有向图和无向图,可以处理带有负权重边的图,但要求图中不能有负权重环。本文将详细介绍Floyd-Warshall算法的定义、步骤及其实现。 Floyd-…...

3DM游戏运行库合集离线安装包2024最新版
3DM游戏运行库合集离线安装包是一款由国内最大的游戏玩家论坛社区3DM推出的集成式游戏运行库合集软件,旨在解决玩家在玩游戏时遇到的运行库缺失或错误问题。该软件包含多种常用的系统运行库组件,支持32位和64位操作系统,能够自动识别系统版本…...

【Bigdata】什么是混合型联机分析处理
这是我父亲 日记里的文字 这是他的生命 留下留下来的散文诗 几十年后 我看着泪流不止 可我的父亲已经 老得像一个影子 🎵 许飞《父亲写的散文诗》 混合型联机分析处理(Hybrid OLAP,简称 HOLAP)是一种结合了多…...

Java 并发编程:volatile 关键字介绍与使用
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 026 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...

【Spark计算引擎----第三篇(RDD)---《深入理解 RDD:依赖、Spark 流程、Shuffle 与缓存》】
前言: 💞💞大家好,我是书生♡,本阶段和大家一起分享和探索大数据技术Spark—RDD,本篇文章主要讲述了:RDD的依赖、Spark 流程、Shuffle 与缓存等等。欢迎大家一起探索讨论!࿰…...

四、日志收集loki+ promtail+grafana
一、简介 Loki是受Prometheus启发由Grafana Labs团队开源的水平可扩展,高度可用的多租户日志聚合系统。 开发语言: Google Go。它的设计具有很高的成本效益,并且易于操作。使用标签来作为索引,而不是对全文进行检索,也就是说&…...

xdma的linux驱动编译给arm使用(中断检测-测试程序)
1、驱动链接 XDMA驱动源码官网下载地址为:https://github.com/Xilinx/dma_ip_drivers 下载最新版本的XDMA驱动源码,即master版本,否则其驱动用不了(xdma ip核版本为4.1)。 2、驱动 此部分来源于博客:xd…...

探索之路——初识 Vue Router:构建单页面应用的完整指南
目录 1. Vue Router 简介 2. 安装与配置 Vue Router 安装步骤 配置路由 3. 在 Vue 应用中使用路由 4. 进阶使用 路由守卫 懒加载 高级路由技术 嵌套路由 动态路由匹配 编程式的路由导航 路由懒加载 路由元信息 在现代前端开发中,单页面应用(SPA)因其出…...

传输层_计算机网络
文章目录 运输层UDPTCPTCP连接管理TCP三次握手TCP四次挥手 可靠机制流量控制拥塞控制 QUIC 运输层 网络层提供了主机之间的逻辑通信 运输层为运行在不同主机上的进程之间提供了逻辑通信 UDP(用户数据报协议)提供一种不可靠、无连接的服务,数据报 TCP(传输控制协议)…...
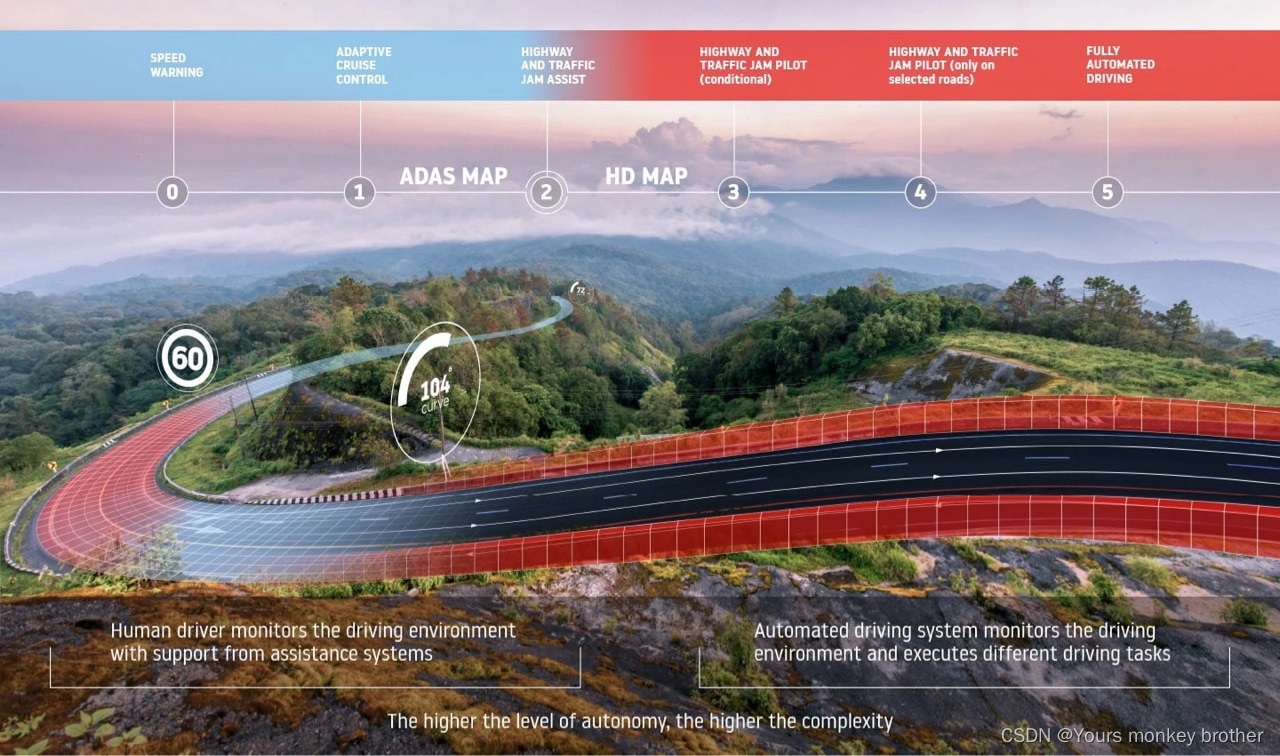
自动驾驶的六个级别是什么?
自动驾驶汽车和先进的驾驶辅助系统(ADAS)预计将帮助拯救全球数百万人的生命,消除拥堵,减少排放,并使我们能够在人而不是汽车周围重建城市。 自动驾驶的世界并不只由一个维度组成。从没有任何自动化到完整的自主体验&a…...

深度学习复盘与论文复现F
文章目录 1、Environment construction1.1 macos conda1.2 macos PyTorch1.3 iTerm settings1.4 install jupyter 2、beam search2.1 greedy search2.2 exhaustive search2.3 beam search 3、Attention score3.1 Masking softmax operation3.2 Additive attention3.3 Zoom dot …...

如何学习自动化测试工具!
要学习和掌握自动化测试工具的使用方法,可以按照以下步骤进行: 一、明确学习目标 首先,需要明确你想要学习哪种自动化测试工具。自动化测试工具种类繁多,包括但不限于Selenium、Appium、JMeter、Postman、Robot Framework等&…...

短信接口被恶意盗刷
短信接口被恶意盗刷是指攻击者通过各种手段,大量发送短信请求,导致短信资源被浪费,服务提供商可能面临经济损失,正常用户的服务也可能受到影响。以下是一些可能导致短信接口被恶意盗刷的原因和相应的解决方案: 原因&a…...

实验4-2-1 求e的近似值
//实验4-2-1 求e的近似值 /* 自然常数 e 可以用级数 11/1!1/2!⋯1/n!⋯ 来近似计算。 本题要求对给定的非负整数 n,求该级数的前 n1 项和。 输入格式:输入第一行中给出非负整数 n(≤1000)。 输出格式:在一行中输出部分和的值,保留…...

内网穿透--LCX+portmap转发实验
实验背景 通过公司带有防火墙功能的路由器接入互联网,然后由于私网IP的缘故,公网 无法直接访问内部web服务器主机,通过内网其它主机做代理,穿透访问内网web 服务器主机 实验设备 1. 路由器、交换机各一台 2. 外网 kali 一台&…...

缓存一致性问题
1. 引言 1.1 数据库与缓存的工程实践 在软件工程领域,数据库(Database)和缓存(Cache)是两种常见的数据存储解决方案,它们在系统架构中扮演着至关重要的角色。数据库是数据持久化的后端存储,它…...

【MYSQL】MYSQL逻辑架构
mysql逻辑架构分为3层 mysql逻辑架构分为3层 1). 连接层:主要完成一些类似连接处理,授权认证及相关的安全方案。 2). 服务层:在 MySQL据库系统处理底层数据之前的所有工作都是在这一层完成的,包括权限判断,SQL接口&…...

【Python】数据类型之字符串
本篇文章将继续讲解字符串其他功能: 1、求字符串长度 功能:len(str) ,该功能是求字符串str的长度。 代码演示: 2、通过索引获取字符串的字符。 功能:str[a] str为字符串,a为整型。该功能是获取字符…...

c++编写java模式的线程类
在 C11 中,我们可以使用 <thread> 标准库来创建和管理线程。然而,C 不像 Java 那样提供一个内置的 Thread 类,而是提供了一个更底层的 API。下面是一个模拟 Java 中 Thread 类功能的 C11 实现。 我们将创建一个名为 SimpleThread 的类…...

vcpkg install libtorch[cuda] -allow-unsupported-compiler
在vcpkg中不懂如何使用 nvcc 的 -allow-unsupported-compiler, 所以直接注释了CUDA中对版本的检查代码. C:\Program Files\NVIDIA GPU Computing Toolkit\CUDA\v11.8\include\crt\host_config.h 奇了怪了,我是用的是vs2022,但是还是被检查为不支持的编译器!!! 可以试一下改这…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
