浅谈基础数论（c++）

一些常见的符号表示

• 整除 （|）：a|b表示b是a的倍数
• 同余符号（$mod$、%、$\equiv ）:a\equiv b(modp)$
• 互质符号$（\perp ）：a\perp b\to gcd(a,b)=1$
• 求和符号($\sum$)
• 连乘符号($\prod$)
• 阶乘符号(!)：$n!=\prod _{i=1}^n(0!=1)$

阶乘

$a,b\in \mathbb{Z}$,且存在$q\in \mathbb{Z}$，使得$b=a\times q$,则称b被a整除，记作a|b，则b是a的倍数，a是b的约数

定理

• a|b且b|c，则a|c
• a|b且b|c，对于任意的$x,y\in \mathbb{Z}$,有a|dx+cy
• $a\ne 0,b=qa+c$，则a整除b的充要条件是a整除c

快速幂

如何求 $x^y$

• 暴力for循环，一边乘法一边取模
• pow(a,b)
• 快速幂
  若 y的二进制表示如下：$y=2^{p_1}+2^{p_2}\dots \dots +2^{p_k}$
  $x^y=x^{2^{p_1}+2^{p_2}\dots \dots +2^{p_k}}$
  $=x^{2^{p_1}}+x^{2^{p_2}}\dots \dots +x^{2^{p_k}}$
  复杂度可以优化到O(log y)

模板题代码

#include <iostream>
#include <algorithm>using namespace std;typedef long long LL;LL qmi(int a, int b, int p)
{LL res = 1 % p;while (b){if (b & 1) res = res * a % p;a = a * (LL)a % p;b >>= 1;}return res;
}int main()
{int n;scanf("%d", &n);while (n -- ){int a, b, p;scanf("%d%d%d", &a, &b, &p);printf("%lld\n", qmi(a, b, p));}return 0;
}

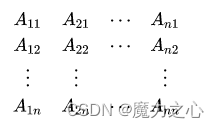
扩展：矩阵快速幂

公式打不动了，粘照片吧

主要作用

优化DP 已达到DDP（动态动态规划）

欧拉函数

定义：欧拉函数$(\varphi )$为正整数n与序列1,2,3,4,5……n-1，n中互质的数的个数（有逆元的个数）
首先对于质数P讨论欧拉函数：

• 对于质数p，$\varphi (p)=p-1$
• 对于一个数n，满足$n=p^k$，那么$\varphi (n)=(p-1)\times p^{k-1}$
  latex已爆炸
  

扩展

积性函数

欧拉函数求法

int phi(int x)
{int res = x;for (int i = 2; i <= x / i; i ++ )if (x % i == 0){res = res / i * (i - 1);while (x % i == 0) x /= i;}if (x > 1) res = res / x * (x - 1);return res;
}

筛选法求欧拉函数（积性函数）

#include<bits/stdc++.h>
using namespace std;
const int N=1000010; 
int prime[N],cnt,phi[N];
bool st[N];
long long get_eulers(int a){phi[1]=1;for(int i=2;i<=a;i++){if(!st[i]){prime[cnt++]=i;phi[i]=i-1;}for(int j=0;prime[j]<=a/i;j++){st[prime[j]*i]=true;if(i%prime[j]==0){phi[prime[j]*i]=prime[j]*phi[i];break;}phi[prime[j]*i]=(prime[j]-1)*phi[i];}}long long res=0;for(int i=1;i<=a;i++)res+=phi[i];return res;} 
int main(){int n;scanf("%d",&n);cout<<get_eulers(n)<<endl;return 0;
}

扩展欧几里得

裴蜀定理

对于两个整数a，b，存在一对整数x,y，满足ax+by=gcd(a,b)

问题

那么，我们如何求解ax+by=gcd（a,b）的任意一组解（x,y）呢？

分析

代码

#include<bits/stdc++.h>
using namespace std;
int exgcd(int a,int b,int &x,int &y){if(!b){x=1,y=0;return a;}int d=exgcd(b,a%b,y,x);y-=a/b*x;return d;
}

问题

若是求ax+by=k的可行解呢？

分析

当且仅当gcd(a,b)|k有解，否则无解
注意：
满足ax+by=gcd（a,b）的（x,y），有很多，假设（x_0,y_0）是其中一组。则所有解为$(x_0+k\frac{b}{gcd(a,b)},y_0-k\frac{a}{a,b}),k\in \mathbb{Z}$
ax+by=d,d|(a,b),则整个方程同除以（a,b）即可

同余与逆元

同余加法、减法、乘法的结果与先做运算再取模结果一致
也就是说$(a\times b)$%p=(a%p)$\times$ (b%p)%p
C++中乘除和取模的优先级同级
需要注意的是，除法并不满足同余，但在很多题目中，由于答案过大常让我们输出答案对一个数取模后的答案，那如果在这种题目中我们遇到除法怎么办？

如何求解逆元

扩展欧几里得

由此可知，逆元存在的条件为gcd（a,m）=1，如果m为质数，则对于任意$0<a<m,a\in \mathbb{Z}$有逆元

例题讲解

X-Magic Pair

题面翻译

给一个数对 $(a,b)$ ，每次可以进行操作 $(a,b)\to (|a-b|,b)$ 或 $(a,|a-b|)$ 。问最后能否令 $a=x$ 或 $b=x$ 。$a,b,x\le 10^{18}$

题目描述

You are given a pair of integers $ (a, b) $ and an integer $ x $ .

You can change the pair in two different ways:

• set (assign) $ a := |a - b| $ ;
• set (assign) $ b := |a - b| $ ,

where $ |a - b| $ is the absolute difference between $ a $ and $ b $ .The pair $ (a, b) $ is called $ x $ -magic if $ x $ is obtainable either as $ a $ or as $ b $ using only the given operations (i.e. the pair $ (a, b) $ is $ x $ -magic if $ a = x $ or $ b = x $ after some number of operations applied). You can apply the operations any number of times (even zero).

Your task is to find out if the pair $ (a, b) $ is $ x $ -magic or not.

You have to answer $ t $ independent test cases.

输入格式

The first line of the input contains one integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The next $ t $ lines describe test cases.

The only line of the test case contains three integers $ a $ , $ b $ and $ x $ ( $ 1 \le a, b, x \le 10^{18} $ ).

输出格式

For the $ i $ -th test case, print YES if the corresponding pair $ (a, b) $ is $ x $ -magic and NO otherwise.

样例 #1

样例输入 #1

8
6 9 3
15 38 7
18 8 8
30 30 30
40 50 90
24 28 20
365 216 52
537037812705867558 338887693834423551 3199921013340

样例输出 #1

YES
YES
YES
YES
NO
YES
YES
YES

思路

首先对题面进行一下分析就会发现题面中有两种操作，假设当前两个数是 $(a,b)(a>=b)$,则在下一步，会分别变成状况一：$(a-b,b)$ 或状况二：$(a,a-b)$，在下一步，第二种情况就会变成状况三：$(a,b)$ 或状况四：$(a-b,b)$,状况三会退回了初始状况，状况四与状况一相同，所以，题面中的两种操作是等价的，那么，接下来的叙述中，只考虑操作一。

$(a,b)$ 操作一之后变为 $(a-b,b)$，如果 $a-b>b$,则变为 $(a-2b,b)$ 否则，变为 $(a-b,2b-a)$。

显然，我们只需要让 $a$ 变成 $a$,之后交换 $a$ 和 $b$ 的位置，再继续递归执行即可

AC代码

#include<bits/stdc++.h>
using namespace std;
inline bool dfs(long long a,long long b,long long x){if(a<b)swap(a,b);if(a==x||b==x)return true;if(a<x)return false;if(a==0||b==0)return false;if(x%b==a%b)return true;return dfs(a%b,b,x);
}
int main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);long long t;cin>>t;while(t--){long long a,b,x;cin>>a>>b>>x;if(dfs(a,b,x))puts("YES");else puts("NO");}
} 

[NOIP2014 普及组] 比例简化

题目背景

NOIP2014 普及组 T2

题目描述

在社交媒体上，经常会看到针对某一个观点同意与否的民意调查以及结果。例如，对某一观点表示支持的有 $1498$ 人，反对的有 $902$ 人，那么赞同与反对的比例可以简单的记为 $1498:902$。

不过，如果把调查结果就以这种方式呈现出来，大多数人肯定不会满意。因为这个比例的数值太大，难以一眼看出它们的关系。对于上面这个例子，如果把比例记为 $5:3$，虽然与真实结果有一定的误差，但依然能够较为准确地反映调查结果，同时也显得比较直观。

现给出支持人数 $A$，反对人数 $B$，以及一个上限 $L$，请你将 $A$ 比 $B$ 化简为 $A^{\prime }$ 比 $B^{\prime }$，要求在 $A^{\prime }$ 和 $B^{\prime }$ 均不大于 $L$ 且 $A^{\prime }$ 和 $B^{\prime }$ 互质（两个整数的最大公约数是 $1$）的前提下，$\frac{A^{\prime }}{B^{\prime }}\ge \frac{A}{B}$ 且 $\frac{A^{\prime }}{B^{\prime }}-\frac{A}{B}$ 的值尽可能小。

输入格式

共一行，包含三个整数 $A,B,L$，每两个整数之间用一个空格隔开，分别表示支持人数、反对人数以及上限。

输出格式

共一行，包含两个整数 $A^{\prime },B^{\prime }$，中间用一个空格隔开，表示化简后的比例。

样例 #1

样例输入 #1

1498 902 10

样例输出 #1

5 3

提示

对于 $100\%$ 的数据，$1\le A\le 10^6,1\le B\le 10^6,1\le L\le 100,\frac{A}{B}\le L$。

思路

我们尽量让a，b互质，即c=1，接着构造，如果两数不互质就加减，直到互质为止

AC代码

#include<bits/stdc++.h>
using namespace std;
inline int gcd(int x,int y)
{if(y==0) return x;return gcd(y,x%y);
}
int main()
{int i,j,a,b,ansa,ansb,l;cin>>a>>b>>l;ansa=l;ansb=1;for(i=1;i<=l;i++)for(j=1;j<=l;j++)if(gcd(i,j)==1&&i*b>=j*a&&i*ansb<j*ansa){ansa=i;ansb=j;}cout<<ansa<<" "<<ansb<<endl;return 0;
}

小凯的数字

题目背景

NOIP2018 原创模拟题T1

NOIP DAY1 T1 or DAY 2 T1 难度

是否发现与NOIP2017 DAY1 T1 有异曲同工之妙

题目描述

小凯有一天突发奇想，写下了一串数字：$\overline{l(l+1)(l+2)...(r-1)r}$

例如：$l=2,r=5$时，数字为：$2345$

$l=8,r=12$时数字为：$89101112$

小凯很喜欢数字 $9$，所以他想问你他写下的数字除以 $9$ 的余数是多少

例如：$l=2,r=5$时，$2345mod9=5$

输入格式

输入格式：

第一行为数字 $Q$,表示小凯有 $Q$ 个问题

第 $2$ 到 $Q+1$ 行，每行两个数字 $l,r$ 表示数字范围

输出格式

输出格式：

对于每行的问题输出一行，一个数字，表示小凯问题的回答

样例 #1

样例输入 #1

2
2 5
8 12

样例输出 #1

5
5

样例 #2

样例输入 #2

3
1 999
123 456
13579 24680

样例输出 #2

0
6
0

提示

样例1解释：$2345mod9=5$ $89101112mod9=5$

30% 数据满足：$Q\le 10;l,r\le 100$

50% 数据满足：$Q\le 100;l,r\le 10000$

70% 数据满足：$Q\le 1000;l,r\le 10^6$

100%数据满足：$Q\le 10000;0<l,r\le 10^{12}$ 且 $l\le r$

AC代码

#include <bits/stdc++.h>
using namespace std;
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--){long long l,r;cin>>l>>r;long long cnt=(r-l+1)%9;;long long ans=cnt*(l%9)%9+(cnt)*(cnt-1)%9*5%9;cout<<ans%9<<endl;}return 0;
}

【模板】二元一次不定方程 (exgcd)

题目描述

给定不定方程

$$ax+by=c$$

若该方程无整数解，输出 $-1$。
若该方程有整数解，且有正整数解，则输出其正整数解的数量，所有正整数解中 $x$ 的最小值，所有正整数解中 $y$ 的最小值，所有正整数解中 $x$ 的最大值，以及所有正整数解中 $y$ 的最大值。
若方程有整数解，但没有正整数解，你需要输出所有整数解中 $x$ 的最小正整数值， $y$ 的最小正整数值。

正整数解即为 $x,y$ 均为正整数的解，$0$ 不是正整数。
整数解即为 $x,y$ 均为整数的解。
$x$ 的最小正整数值即所有 $x$ 为正整数的整数解中 $x$ 的最小值，$y$ 同理。

输入格式

第一行一个正整数 $T$，代表数据组数。

接下来 $T$ 行，每行三个由空格隔开的正整数 $a,b,c$。

输出格式

$T$ 行。

若该行对应的询问无整数解，一个数字 $-1$。
若该行对应的询问有整数解但无正整数解，包含 $2$ 个由空格隔开的数字，依次代表整数解中，$x$ 的最小正整数值，$y$ 的最小正整数值。
否则包含 $5$ 个由空格隔开的数字，依次代表正整数解的数量，正整数解中，$x$ 的最小值，$y$ 的最小值，$x$ 的最大值，$y$ 的最大值。

读入输出量较大，注意使用较快的读入输出方式

样例 #1

样例输入 #1

7
2 11 100
3 18 6
192 608 17
19 2 60817
11 45 14
19 19 810
98 76 5432

样例输出 #1

4 6 2 39 8
2 1
-1
1600 1 18 3199 30399
34 3
-1
2 12 7 50 56

提示

【数据范围】

对于 $100\%$ 的数据，$1\le T\le 2\times {10}^5$，$1\le a,b,c\le {10}^9$。

AC代码

#include<bits/stdc++.h>
using namespace std;
long long gcd(long long n,long long m)
{return (n%m==0)?m:gcd(m,n%m);
}
void exgcd(long long a,long long b,long long &x,long long &y)
{if(!b){x=1;y=0;return;}long long p;exgcd(b,a%b,x,y);p=x;x=y;y=p-(a/b)*y;return;
}
int t;
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);cin>>t;while(t--){long long x=0,y=0,a,b,c,g,xin,yin,xax,yax,npa=0,k;cin>>a>>b>>c;g=gcd(a,b);if(c%g!=0)cout<<"-1"<<endl;else{a/=g,b/=g,c/=g;exgcd(a,b,x,y);x*=c,y*=c;xin=x>0&&x%b!=0?x%b:x%b+b;yax=(c-xin*a)/b;yin=y>0&&y%a!=0?y%a:y%a+a;xax=(c-yin*b)/a;if(xax>0)npa=(xax-xin)/b+1;if(!npa)cout<<xin<<" "<<yin<<endl;else cout<<npa<<" "<<xin<<" "<<yin<<" "<<xax<<" "<<yax<<endl;}}return 0;
}

【模板】模意义下的乘法逆元

题目背景

这是一道模板题

题目描述

给定 $n,p$ 求 $1\sim n$ 中所有整数在模 $p$ 意义下的乘法逆元。

这里 $a$ 模 $p$ 的乘法逆元定义为 $ax\equiv 1(\mathrm{mod}p)$ 的解。

输入格式

一行两个正整数 $n,p$。

输出格式

输出 $n$ 行，第 $i$ 行表示 $i$ 在模 $p$ 下的乘法逆元。

样例 #1

样例输入 #1

10 13

样例输出 #1

1
7
9
10
8
11
2
5
3
4

提示

$ 1 \leq n \leq 3 \times 10 ^ 6$，$n < p < 20000528 $。

输入保证 $ p $ 为质数。

AC代码

#include <bits/stdc++.h>
const int N = 3000010;
int n, p;
int inv[N], factinv[N];
int main() {scanf("%d%d", &n, &p);factinv[1] = inv[1] = 1;printf("%d\n", 1);for (int i = 2; i <= n; ++i) {inv[i] = 1ll * (p - p / i) * inv[p % i] % p;printf("%d\n", inv[i]);factinv[i] = 1ll * factinv[i - 1] * inv[i] % p;}return 0;
}

注意

本题的时间限制较小，只能写O（1）的递推算法

[SDOI2008] 仪仗队

题目描述

作为体育委员，C 君负责这次运动会仪仗队的训练。仪仗队是由学生组成的 $N\times N$ 的方阵，为了保证队伍在行进中整齐划一，C 君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐（如下图）。

现在，C 君希望你告诉他队伍整齐时能看到的学生人数。

输入格式

一行，一个正整数 $N$。

输出格式

输出一行一个数，即 C 君应看到的学生人数。

样例 #1

样例输入 #1

4

样例输出 #1

9

提示

对于 $100\%$ 的数据，$1\le N\le 40000$。

思路

如果一个位置可以被看见，那么不难证明，它的x，y坐标互质
理由如下，如果x与y不互质，则一定有一个c=gcd(x,y)
且一定存在xx=x/c,yy=y/c
则x,y会被挡住，与假设不符

AC代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<queue>
#include<algorithm>
using namespace std;
typedef long long ll;const int maxn=50000;int vis[maxn];
int prime[maxn];
int phi[maxn];
int sum[maxn];int main()
{phi[1]=1;sum[1]=1;int k=-1;for(int i=2;i<=40000;i++){if(!vis[i]){prime[++k]=i;phi[i]=i-1;}for(int j=0;j<=k&&i*prime[j]<=40000;j++){vis[i*prime[j]]=1;if(i%prime[j]==0){phi[i*prime[j]]=phi[i]*prime[j];break;}phi[i*prime[j]]=phi[i]*phi[prime[j]];}sum[i]=sum[i-1]+phi[i];}int n;scanf("%d",&n);if(n==1)printf("0\n");elseprintf("%d\n",2*sum[n-1]+1);return 0;
}

Array

题面翻译

描述

对于长度为n的数组A，A中只包含从1到n的整数（可重复）。如果A单调不上升或单调不下降，A就可称为美丽的。
找出在长度为n时，有几个美丽的A。

输入

一个整数n,(1<=n<=10^5)

输出

输出长度为n时，有几个美丽的A，由于答案可能非常的大，输出时需要将答案对1000000007取模.

Translated by KethGeorge

题目描述

Chris the Rabbit has been interested in arrays ever since he was a child. At the moment he is researching arrays with the length of $ n $ , containing only integers from $ 1 $ to $ n $ . He is not good at math, that’s why some simple things drive him crazy. For example, yesterday he grew keen on counting how many different beautiful arrays there are. Chris thinks that an array is beautiful if it meets one of the two conditions:

• each elements, starting from the second one, is no more than the preceding one
• each element, starting from the second one, is no less than the preceding one

Having got absolutely mad at himself and at math, Chris came to Stewie and Brian to ask them for help. However, they only laughed at him and said that the answer is too simple and not interesting. Help Chris the Rabbit to find the answer at last.

输入格式

The single line contains an integer $ n $ which is the size of the array ( $ 1<=n<=10^{5} $ ).

输出格式

You must print the answer on a single line. As it can be rather long, you should print it modulo $ 1000000007 $ .

样例 #1

样例输入 #1

2

样例输出 #1

4

样例 #2

样例输入 #2

3

样例输出 #2

17

思路

首先，因为不增和不降是相对称的，所以我们只用从一个角度入手进行计算。
其次，运用隔板法，推出排列组合序列

AC代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int mod=1e9+7,N=1e5+233;
int n,ans=1,et[N];
signed main(){cin>>n;et[1]=1;for(int i=2;i<=n;i++)et[i]=(mod-mod/i)*et[mod%i]%mod; for(int i=1;i<=n;i++)ans=ans*et[i]%mod*(n+i)%mod;cout<<((ans-n)%mod+mod)%mod;return 0;
}

测测你的矩阵乘法

题目描述

给定两个大小为均为 $512\times 512$，每个元素均为整数，值域为 $ [0, 1024) $ 矩阵 $A,B$，定义为

$$\begin{array}{rl}A\left[i,j\right]& =\left(\left(i\mathrm{or}j\right)+j\right)\mathrm{xor}{\mathrm{seed}}_A\\ B\left[i,j\right]& =\left(\left(i\mathrm{and}j\right)+i\right)\mathrm{xor}{\mathrm{seed}}_B\end{array}$$

其中 $i,j\in [0,512)$。

请计算 $C=A\times B$。

输入格式

输入为两个整数 ${\mathrm{seed}}_A,{\mathrm{seed}}_B$（$0\le {\mathrm{seed}}_A,{\mathrm{seed}}_B<1024$）。

你可以使用以下代码模板，完成其中的 multiply 即可。

你可以修改 $N$（即数组长度），但是不能修改 $n$（矩阵大小，恒为 $512$）。

#include <bits/stdc++.h>
const int n = 512, N = n;
void multiply (int c[N][N], int a[N][N], int b[N][N]) {// c = a * b
}
int c[N][N], a[N][N], b[N][N];
int main() {int seedA, seedB;scanf("%d%d", &seedA, &seedB);for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)a[i][j] = ((i | j) + j) ^ seedA;for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)b[i][j] = ((i & j) + i) ^ seedB;multiply(c, a, b);for (int i = 0; i < n; i++) {int sum = 0;for (int j = 0; j < n; j++) sum ^= c[i][j];printf("%d\n", sum);}
}

输出格式

输出 $512$ 行，分别是 $C$ 每行的异或和。

输入中的代码会帮助你完成输出。

样例 #1

样例输入 #1

0 0

样例输出 #1

8126464
14942208
33554432
...(省略506行)
29097984
146800640
148570112

题面有点奇怪

#include <bits/stdc++.h>
const int n = 512, N = n;
void multiply (int c[N][N], int a[N][N], int b[N][N]) {for(int i = 0; i < N; i++) {for(int j = 0; j < N; j++) {for(int k = 0; k < N; k++) {c[i][j] += a[i][k] * b[k][j];}}} 
}
int c[N][N], a[N][N], b[N][N];
int main() {int seedA, seedB;scanf("%d%d", &seedA, &seedB);for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)a[i][j] = ((i | j) + j) ^ seedA;for (int i = 0; i < n; i++)for (int j = 0; j < n; j++)b[i][j] = ((i & j) + i) ^ seedB;multiply(c, a, b);for (int i = 0; i < n; i++) {int sum = 0;for (int j = 0; j < n; j++) sum ^= c[i][j];printf("%d\n", sum);}return 0;
}

这是我的第十四篇文章，如有纰漏也请各位大佬指正

辛苦创作不易，还望看官点赞收藏打赏，后续还会更新新的内容。