基于FPGA的数字信号处理（20）--半减器和全减器

目录

1、前言

2、半减器

3、全减器

4、减法器

---

         文章总目录点这里：《基于FPGA的数字信号处理》专栏的导航与说明

---

1、前言

        既然有半加器和全加器，那自然也有半减器和全减器了。尽管在电路中减法的实现基本都是 补码 + 加法 的形式，但是正所谓技多不压身，了解一下半减器和全减器还是有一定作用的，至少能扩宽知识面嘛。

2、半减器

        最简单的减法器叫做 半减器（Half Subtractor），它将2个1bit的输入数据相减，输出一个1bit的结果即 差Di（Difference），以及向高位的借位Bo（Borrow output）。例如：

• 1 - 1 = 01 -1 = 0，不需要向高位借位，差为0，即Bo = 0，Di = 0

• 1 - 0 = 01 -0 = 1，不需要向高位借位，差为1，即Bo = 0，Di = 1

• 0 - 1 = 10 -1 = 1， 需要向高位借位，差为1，即Bo = 1，Di = 1

• 0 - 0 = 00 -0 = 0，不需要向高位借位，差为0，即Bo = 0，Di = 0

        2个1bit数相减，最多只有4种情况（在上面已经例出来了），据此可以写出半减器的真值表：

被减数	减数	差	向高位借位
X	Y	Di	Bo
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

        从这个真值表，不难推断出输出的逻辑表达式：

• 差Di在2个输入不同时为1，所以它是输入异或的结果，即 Di = a ^ b

• 向高位借位Bo在X = 0 且 Y = 1 时才为1，即 Bo= ~X & Y

        有了逻辑表达式后，可以很容易地画出对应的门电路结构：

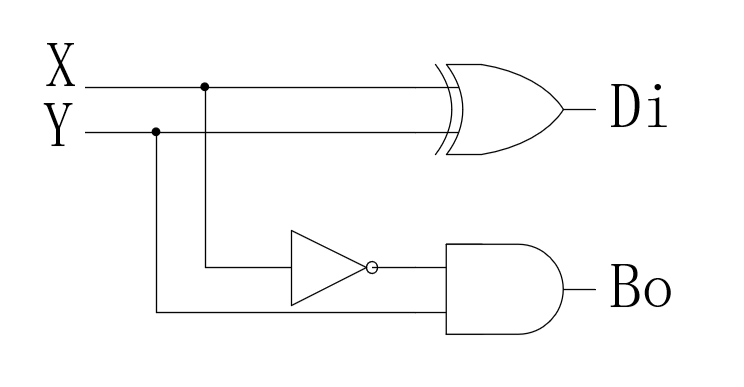
        顺便提一句，虽然半减器的基本电路是上面这个样子的，但是因为在FPGA中只有查找表LUT而没有具体的门电路，所以如果用FPGA来综合半减器的话，它的电路应该是这个样子的（因为只有2个输入和2个输出，所以只要1个LUT6就可以覆盖到所有情况）：

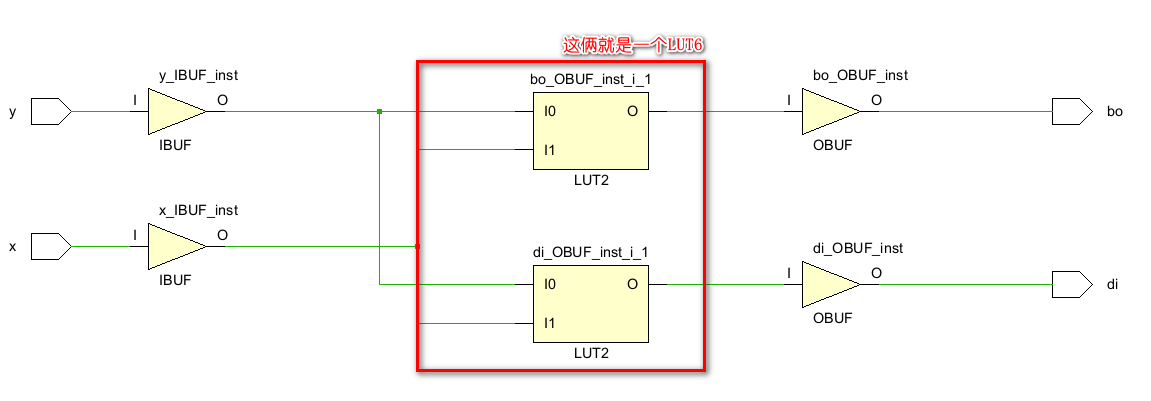
如果你不了解LUT，可以看看这篇文章：从底层结构开始学习FPGA（2）----LUT查找表，或者看看这个专栏：从底层结构开始学习FPGA

        IBUF和OBUF是Vivado自动添加的对输入输出管脚的缓冲，尽管上图显示的是2个LUT2（可能这样的显示更清晰一点），但是实际上就是1个LUT6，下面的资源显示情况也证明了这一点：

        用verilog实现半减器如下：

//使用逻辑表达式来描述半减器
module half_subtractor(input   x,      //被减数input   y,      //减数output  di,     //差output  bo      //向高位借位
);
​
//根据化简结果分别表示：差 与 向高位借位
assign di = x ^ y;  
assign bo = ~x & y;endmodule

        有了RTL，接下来就该要写个对应的TB来测试电路功能是否正常。由于这个电路足够简单（一共只有4种情况），所以我们可以把所有可能的情况都穷举出来，然后观察输出是否符合预期即可。TB如下：

`timescale 1ns/1ns              //时间刻度：单位1ns,精度1ns
​
module tb_half_subtractor();            
​
//定义变量  
reg     x;
reg     y;
wire    di;
wire    bo;
​
//设置初始化条件
initial begin//第1种情况x =1'b0;    y =1'b0;    #10     //第2种情况x =1'b0;    y =1'b1;    #10     //第3种情况x =1'b1;    y =1'b0;#10     //第4种情况x =1'b1;    y =1'b1;#10 $stop();    //结束仿真  
end
​
//例化被测试模块
half_subtractor u_half_subtractor(.x      (x),.y      (y),    .di     (di),   .bo     (bo)
);endmodule

        仿真结果如下：

        通过和真值表的对比（或者验证逻辑表达式也可以），可以发现，电路的输出是符合预期的。

3、全减器

        虽然半减器可以实现2个1bit数的减法，但在实际应用中，更常见的是要实现2个多bits数的减法，那么该如何实现？以2个2bits数的减法为例：

1. 先把低位和高位的减法先分开。

2. 低位是2个1bit的减法，所以可以用1个HS（半减器）来实现，它产生的差就是最终结果的低位，它产生的向高位借位要被送入到高位参与它们的减法。

3. 高位除了要计算减数和被减数的高位外，还有1个来自低位的借位。

        好，现在问题是半减器没有设计来自低位的借位，所以它处理不了这种情况。为此，全减器被设计出来了，它在半减器的基础上，增加了来自低位的借位输入。这样多个全减器就可以级联起来实现多bits的减法了。

        全减器（Full Subtractor），它处理2个1bit的输入和来自低位的借位Bi（Borrow input）输入共3个数，输出一个差Di和向高位的借位Bi。例如（格式：被减数- 减数 - 来自低位的借位）：

• 1 - 1 - 1 = 11 - 1 - 1 = 0，来自低位的借位为1， 需要向高位借位，差为0，即Bi = 1，Bo = 0，Di = 0

• 1 - 1 - 0 = 01 - 1 - 0 = 0，来自低位的借位为0，不需要向高位借位，差为0，即Bi = 0，Bo = 0，Di = 0

• 1 - 0 - 1 = 01 - 0 - 1 = 0，来自低位的借位为1，不需要向高位借位，差为0，即Bi = 1，Bo = 0，Di = 0

• 1 - 0 - 0 = 01 - 0 - 0 = 0，来自低位的借位为0，不需要向高位借位，差为1，即Bi = 0，Bo = 0，Di = 1

• ······

        3个输入一共只有8种情况，把所有情况都穷举出来，就可以列出全减器的真值表：

被减数	减数	来自低位的借位	差	向高位的借位
X	Y	Bi	Di	Bo
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

        从这个真值表，不难推断出两个输出的逻辑表达式：

• Di为1的4种情况，~x&~y&bi + ~x&y&~bi + x&~y&~bi + x&y&bi=~x&(~y&bi+y&~bi)+x&(~y&~bi+y&bi) = ~x&(y^bi) + x&~(y^bi) = x ^ y ^ bi

• Bo为1的4种情况，~x&~y&bi + ~x&y&~bi + ~x&y&bi + x&y&bi = ~x&(~y&bi+y&~bi) + (~x+x)&y&bi = ~x&(y^bi) + y&bi

        有了逻辑表达式后，就很容易画出电路图了（偷了个懒，不是画的，是用vivado生成的）：

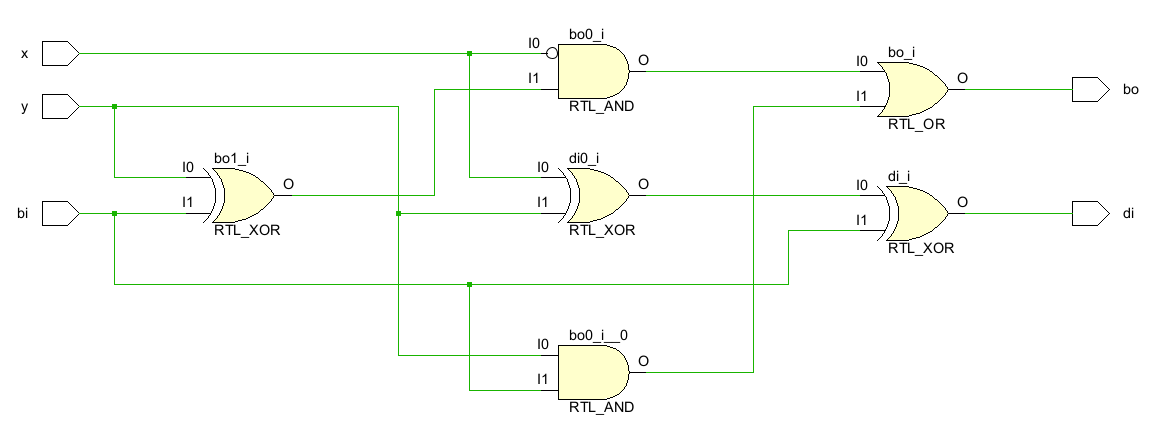
        根据门电路，可以写出全减器的Verilog实现：

//使用逻辑表达式来描述全减器
module full_subtractor(input   x,      //被减数input   y,      //减数input   bi,     //来自低位的借位output  di,     //差output  bo      //向高位借位
);
​
//根据化简结果分别表示：差 与 向高位借位
assign di = x ^ y ^ bi; 
assign bo = ~x & (y ^ bi) | y & bi;endmodule 

        接下来写个TB测试电路，输入一共只有8个，所以依然用穷举法来测试：

`timescale 1ns/1ns              //时间刻度：单位1ns,精度1ns
​
module tb_full_subtractor();            
​
//定义变量  
reg     x;
reg     y;
reg     bi;
wire    di;
wire    bo;
​
//设置初始化条件
initial begin//第1种情况x =1'b0;    y =1'b0;    bi =1'b0;   #10     //第2种情况x =1'b0;    y =1'b1;bi =1'b0;   #10     //第3种情况x =1'b1;    y =1'b0;bi =1'b0;#10     //第4种情况x =1'b1;    y =1'b1;bi =1'b0;#10     //第5种情况x =1'b0;    y =1'b0;    bi =1'b1;#10     //第6种情况x =1'b0;    y =1'b1;bi =1'b1;#10     //第7种情况x =1'b1;    y =1'b0;bi =1'b1;#10     //第8种情况x =1'b1;    y =1'b1;bi =1'b1;   #10 $stop();    //结束仿真  
end
​
//例化被测试模块
full_subtractor u_full_subtractor(.x      (x),.y      (y),    .di     (di),.bi     (bi),.bo     (bo)
);endmodule

        仿真结果如下所示：

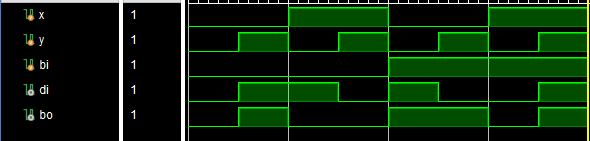
        通过和真值表的对比（或者验证逻辑表达式也可以），可以发现，电路的输出是符合预期的。

4、减法器

        有了全减器后，就可以实现两个多bits数的减法了，这样的电路也被称为减法器。和行波进位加法器的结构类似，我们也可以将多个全减器级联起来搭建减法器，以4bits的减法为例，它的结构如下：

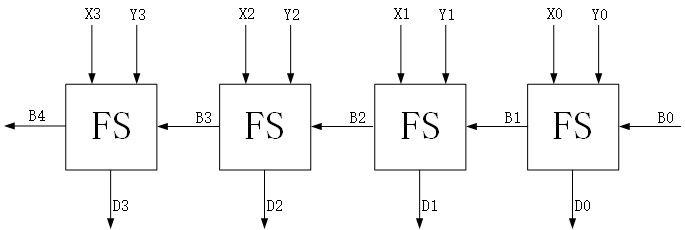
        根据结构图，可以很快地写出它对应的Verilog代码：

//使用多个全减器建联构建减法器
module subtractor(input   [3:0]   x,  //被减数input   [3:0]   y,  //减数input           bi, //来自低位的借位output  [3:0]   di, //差output          bo  //向高位借位
);
​
wire    b1,b2,b3;   //借位连接
​
//例化全减器来构建减法器
full_subtractor u0(.x      (x[0]),.y      (y[0]), .di     (di[0]),.bi     (bi),.bo     (b1)
);
full_subtractor u1(.x      (x[1]),.y      (y[1]), .di     (di[1]),.bi     (b1),.bo     (b2)
);
full_subtractor u2(.x      (x[2]),.y      (y[2]), .di     (di[2]),.bi     (b2),.bo     (b3)
);
full_subtractor u3(.x      (x[3]),.y      (y[3]), .di     (di[3]),.bi     (b3),.bo     (bo)
);
​
endmodule

        这里记得要把之前的全减器也添加进工程。生成的示意图如下（这个排布不能很好地看出来层次结构，但确实没错）：

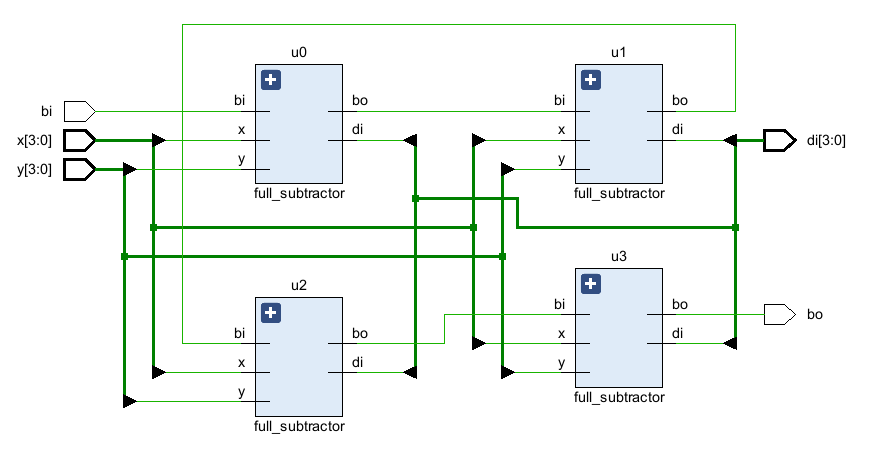
        然后写个TB测试一下这个减法器电路，因为4个bits即16×16=256种情况，加上低位借位的两种情况，也才256×2=512种情况，所以依然用穷举法来测试：

`timescale 1ns/1ns              //时间刻度：单位1ns,精度1ns
​
module tb_full_subtractor();            
​
//定义变量  
reg     [3:0]   x;      //被减数
reg     [3:0]   y;      //减数
reg             bi;     //来自低位的借位
wire    [3:0]   di;     //差
wire            bo;     //向高位借位
​
reg [3:0]   di_real;    //差的真实值，作为对比
reg         bo_real;    //向高位借位的真实值，作为对比
wire        di_flag;    //di正确标志信号
wire        bo_flag;    //bo正确标志信号
​
assign di_flag = di == di_real; //di结果正确时拉高该信号
assign bo_flag = bo == bo_real; //bo结果正确时拉高该信号
​
integer z,i,j;  //循环变量
//设置初始化条件
initial begin//初始化x =1'b0;    y =1'b0;    bi =1'b0;   //设定低位借位为0//穷举所有情况for(z=0;z<=1;z=z+1)beginbi = z;for(i=0;i<16;i=i+1)beginx = i;for(j=0;j<16;j=j+1)beginy = j;if((i-j-z)<0)begin                  //减法结果是负数di_real = (i - j - z)+ 5'd16;   //加上向高位的借位bo_real = 1;                    //向高位的借位为1endelse begin                          //减法结果是正数数di_real = i - j - z;            //结果就是减法本身bo_real = 0;                    //向高位的借位为0end#5;             end endend#10 $stop();    //结束仿真  
end
​
//例化被测试模块
subtractor u_subtractor(.x      (x),.y      (y),    .di     (di),.bi     (bi),.bo     (bo)
);endmodule

        TB中分别用3个嵌套循环将所有情况穷举出来，即bi=0~1、x=0~15和y=0~15的所有情况。减法运算的预期结果也是很容易就可以找出来的，就是直接写减法就行。接着构建了两个标志向量di_flag和bo_flag作为电路输出与预期结果的对比值，当二者一致时即拉高这两个信号。这样我们只要观察这两个信号，即可知道电路输出是否正确。仿真结果如下：

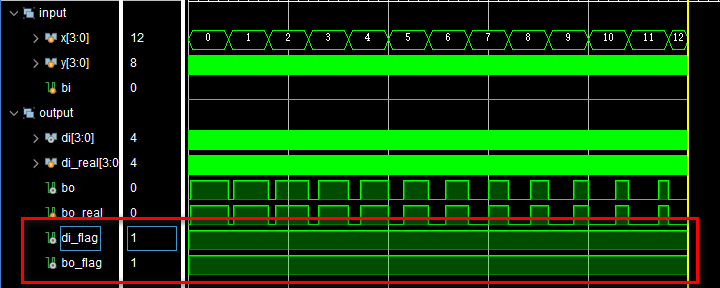
        可以看到，di_flag和bo_flag都是一直拉高的，说明电路输出正确。