C++分析红黑树

目录

红黑树介绍

红黑树的性质与平衡控制关系

红黑树节点的插入

情况1：不需要调整

情况2：uncle节点为红色

情况3：uncle节点为黑色

总结与代码实现

红黑树的删除（待实现）

红黑树的效率

---

红黑树介绍

红黑树是第二种平衡二叉搜索树，为了解决普通二叉搜索树的效率问题，红黑树在控制平衡时选择近似平衡而不是AVL树的绝对平衡，每一个节点都会存储一个表示颜色的属性，包括红色和黑色，通过对颜色的控制，红黑树可以保证没有一条路径会比其他路径的长度长出两倍

红黑树的性质

1. 根节点一定是黑色
2. 一条简单路径下不会出现连续的红色节点，如果父亲节点为红色，则其孩子节点一定为黑色，如果父亲节点为黑色，则没有限制
3. 对于每个节点来说，从该节点开始到其后代所有节点的简单路径上均包含相同数量的黑色节点
4. （了解）每个空叶子结点都是黑色的

在上图中，NIL表示空叶子节点，以NIL作为结束条件，一共有11条路径，需要注意不是以叶子节点为结束条件（即不是7条路径）

满足上面的四个性质，红黑树就可以保证其相对平衡的条件：红黑树可以保证最长路径会比最短路径的长度长出两倍。

最短路径：节点颜色为全黑的路径，此时黑色节点的个数即为路径的长度
最长路径：节点颜色为红色和黑色交替出现的路径

红黑树的性质与平衡控制关系

因为黑色节点的个数可以决定一条路径的长度，假设黑色节点的个数为h，则最短路径的长度也为h，满足第二条规则时，红色节点的个数不会超过黑色节点（1个或者h个），从而最长路径的最大长度为2h，因为红色节点是在黑色节点出现后才会出现。

如果按照下图的插入方式导致红色节点连续出现：

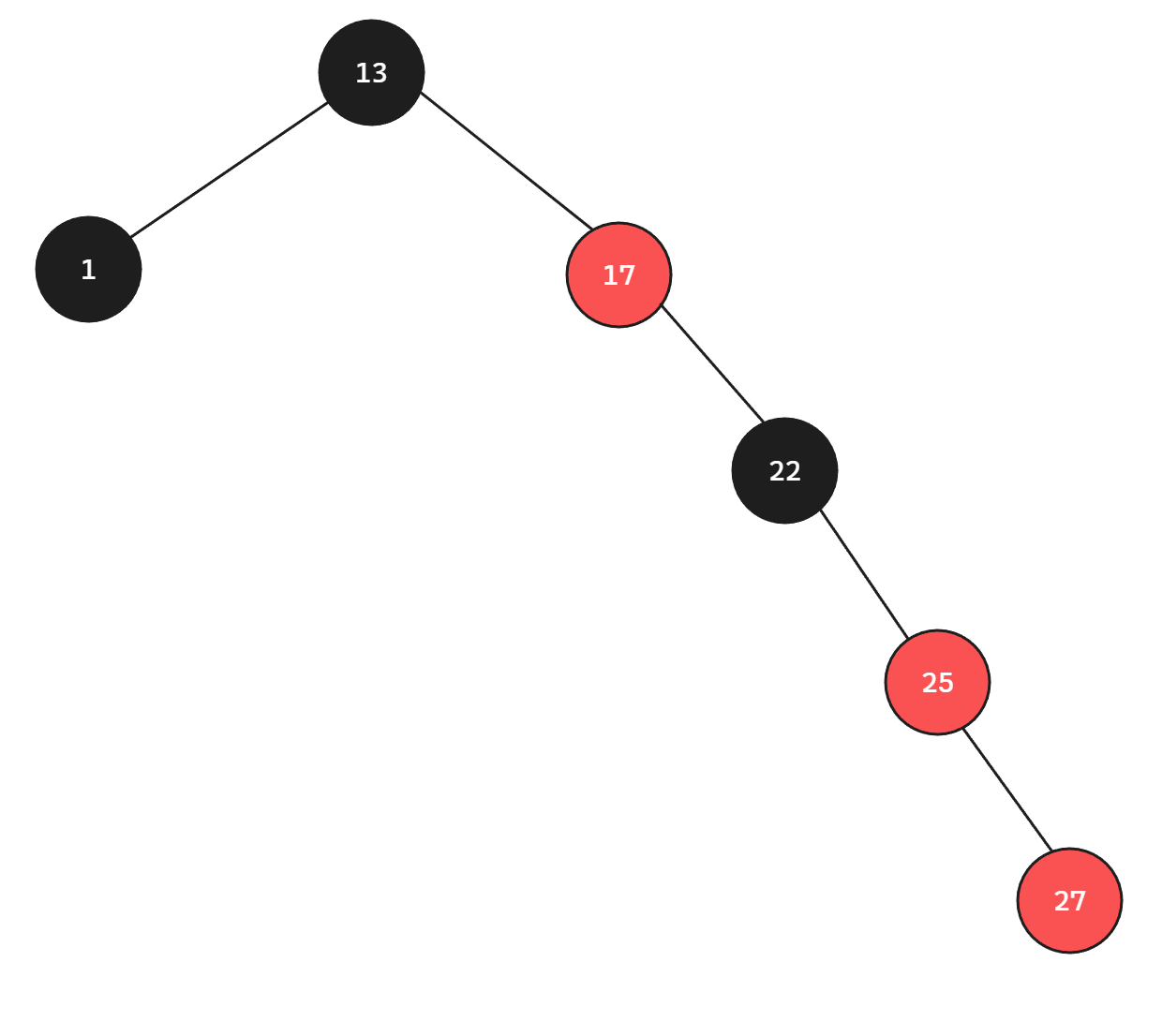
违反了规则二，此时最短路径的长度的两倍会小于最长路径的长度，从而打破了红黑树的平衡。

如果插入的27为黑色节点，则最长路径的长度增加，并且黑色节点的个数也增加，违反了规则三，此时对于其他路径来说也需要增加一个黑色节点。

所以为了维持平衡，不可以插入黑色节点，此时最长路径的长度刚好为2h，如下图所示：

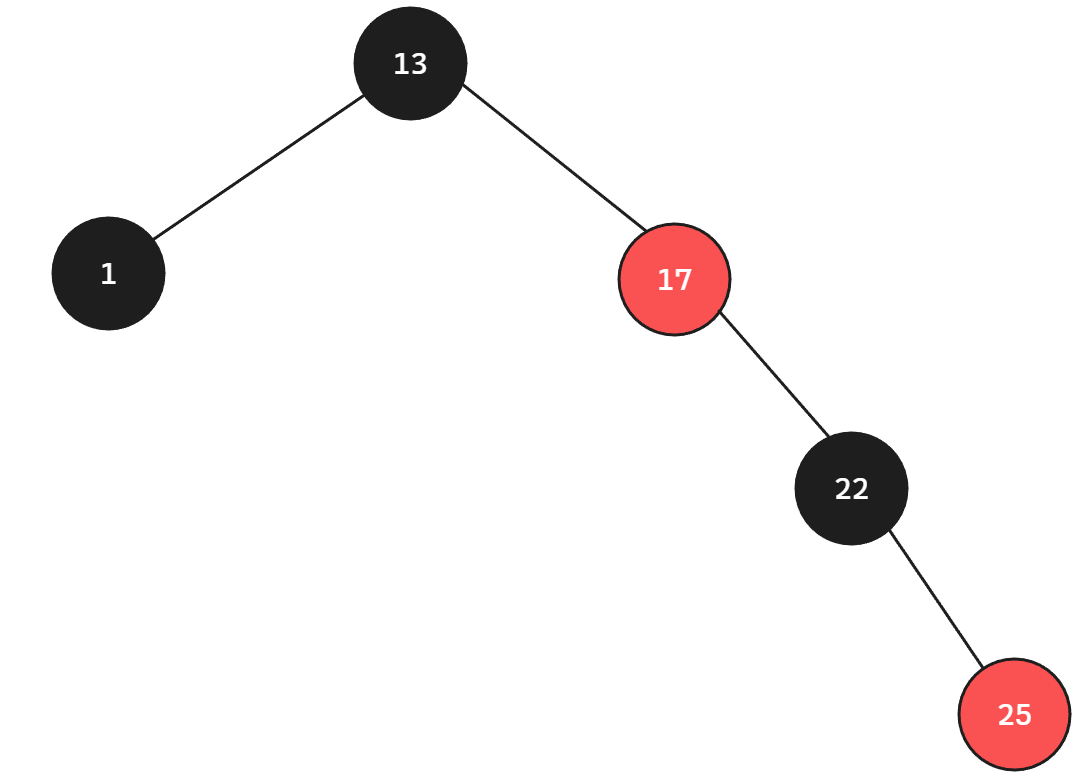
综上所述，在满足第二条规则和第三条规则下可以保证红黑树的最长路径始终不会超过最短路径的2倍

红黑树节点的插入

根据红黑树的性质可以看出红黑树如何控制高度近似平衡，但是如果插入了节点，可能会破坏原有的平衡，此时需要通过重新填色或者旋转调整使红黑树重新达到平衡

在前面的分析中可以得知，如果插入的节点是黑色节点，可能会导致每一条路径都需要多一个黑色节点，为了更加方便处理，规定插入的节点是红色节点

情况1：不需要调整

如果插入的节点是红色节点，并且其父亲节点是黑色节点，此时不需要进行任何处理，当父亲节点是黑色节点时，保证了规则三没有违背，因为黑色节点的个数决定了高度，插入前如果保证原树是红黑树，那么高度一定满足红黑树的近似平衡，并且此时插入红色节点也不会违背规则二，如下图的一种情况所示：

情况2：uncle节点为红色

如果cur的节点是红色，并且其父亲节点（假设为parent）是红色节点，此时说明父亲的兄弟节点（假设为uncle）也一定为红色，因为插入前一定是红黑树（插入前不是红黑树那么插入前就已经出现了不平衡，需要进行调整），当父亲节点时红色，说明父亲节点所在的路径缺少黑色节点，违反了规则三。父亲节点的父亲节点（假设为grandfather）也一定为黑色，如果为红色则违反了第二条规则所以插入前的状态应该为：

cur节点可能为新增的红色节点，也可能为上一次调整变为的红色节点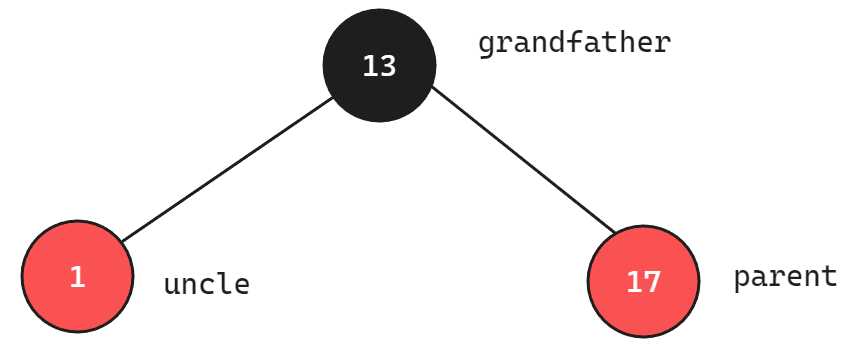

1. 假设a、b、c、d和e为黑色节点个数为0的红黑树，此时cur为新插入节点如下图所示：

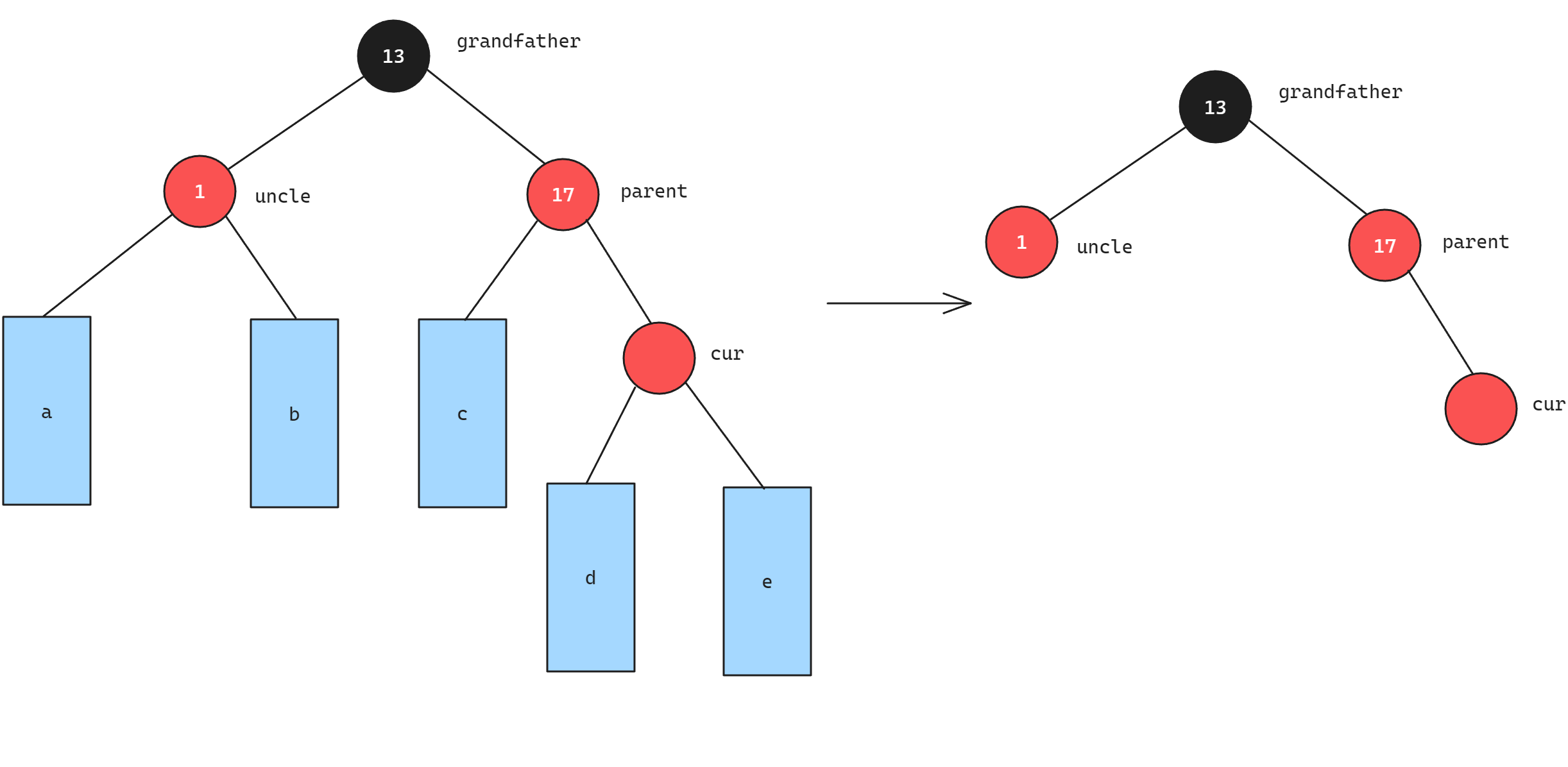
因为出现了连续的红色节点，为了恢复红黑树的平衡，此时需要进行调整，因为uncle节点为红色，为了保证每条路径上都有一个黑色节点并且保证没有连续的红色节点出现，将parent节点的颜色改为黑色，将uncle节点的颜色改为黑色，将grandfather节点改为红色（如果grandfather节点为根节点则再处理为黑色），处理完后，cur = grandfather继续向上调整直到遇到根节点：

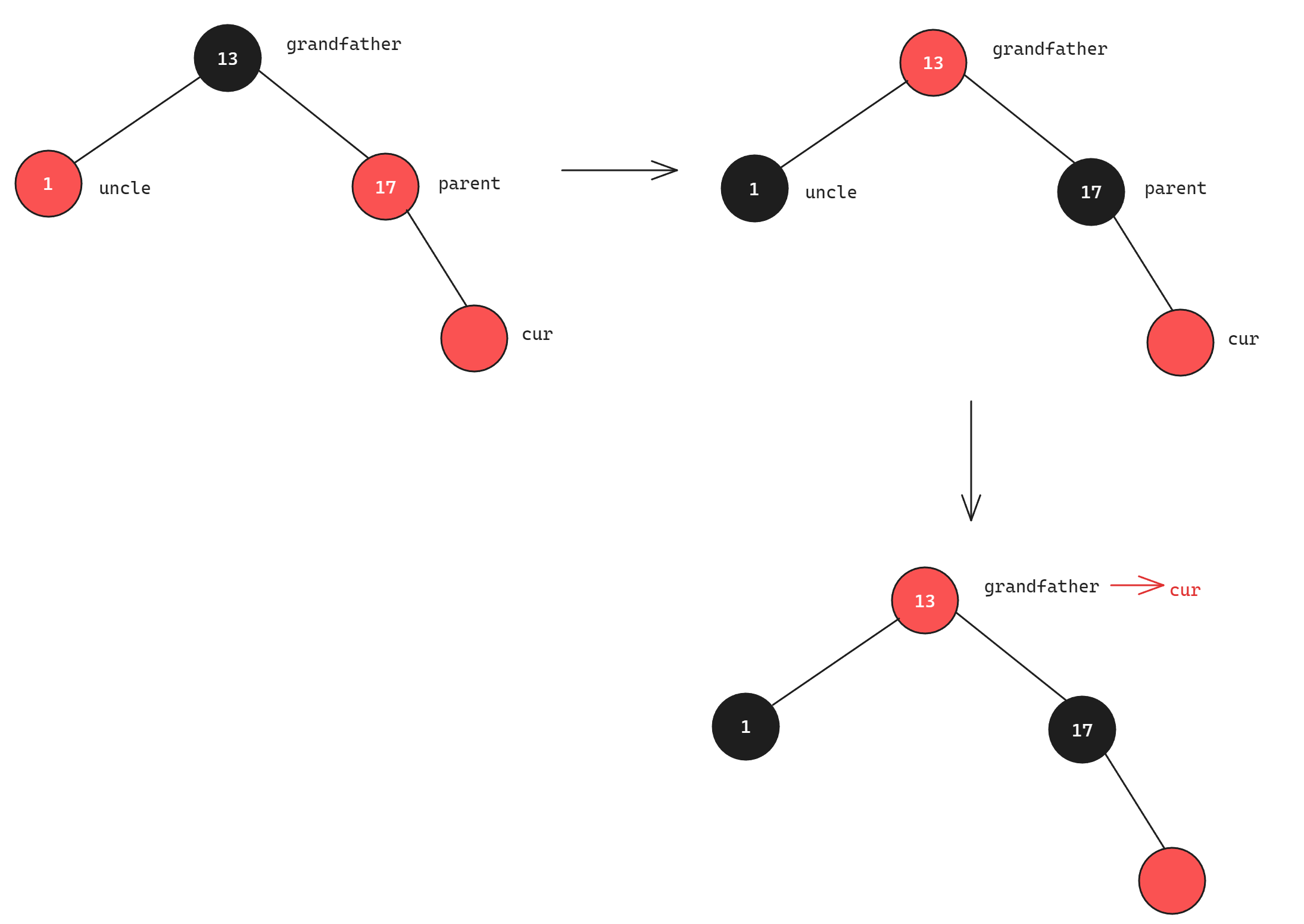
对于 uncle为红色的情况来说，不需要考虑插入位置在 parent左或者右、 parent在 grandfather的左或者右已经 uncle在 grandfather的左或者右，因为不论是哪种情况，本质都是将 uncle和 parent变为黑色增加两边路径的黑色节点使其满足规则二和规则三

1. 假设a、b、c、d和e为黑色节点个数大于0，此时cur为上一次调整变成的红色节点，如下图所示：

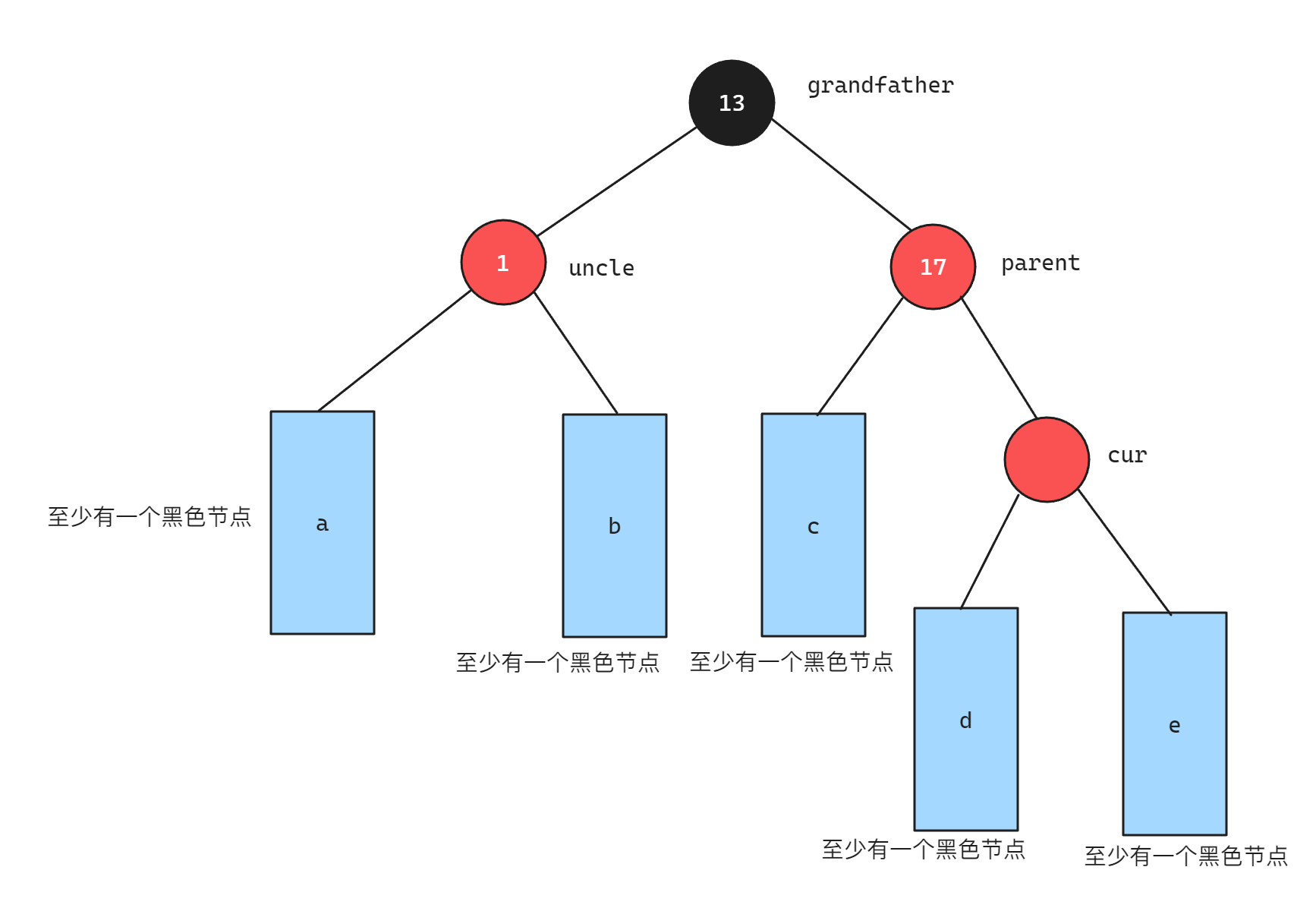
对于当前情况来说，只有cur位置的节点是红色，其余几棵子树已经通过调整变成了符合规则的红黑树，所以也可以归类为上面的情形，处理方式与上面相同

情况3：uncle节点为黑色

uncle节点为黑色时一共有两种情况：

1. uncle节点不存在
2. uncle节点存在且为黑

因为红黑树规定下空节点是黑色的，所以uncle节点不存在与存在且为黑可以视为一种情况，下面主要以uncle节点不存在进行分析，对于uncle节点存在且为黑的情况给出一种分析，剩下与uncle节点不存在的情况类似

下面分析中， uncle节点不存在时将不展示 NIL节点

当cur节点在parent的右子树并且parent在grandfather的右子树时，并且uncle不存在时，此时需要进行左单旋，将parent的颜色更新为黑色，grandfather的颜色更新为红色，因为如果仅仅是将parent变成黑色，则依旧不满足规则三，其余路径还是少一个黑色节点，通过左单旋使得当前子树的根节点变为黑色时可以使当前根节点出发的所有路径都至少有一个黑色节点，如下图所示：

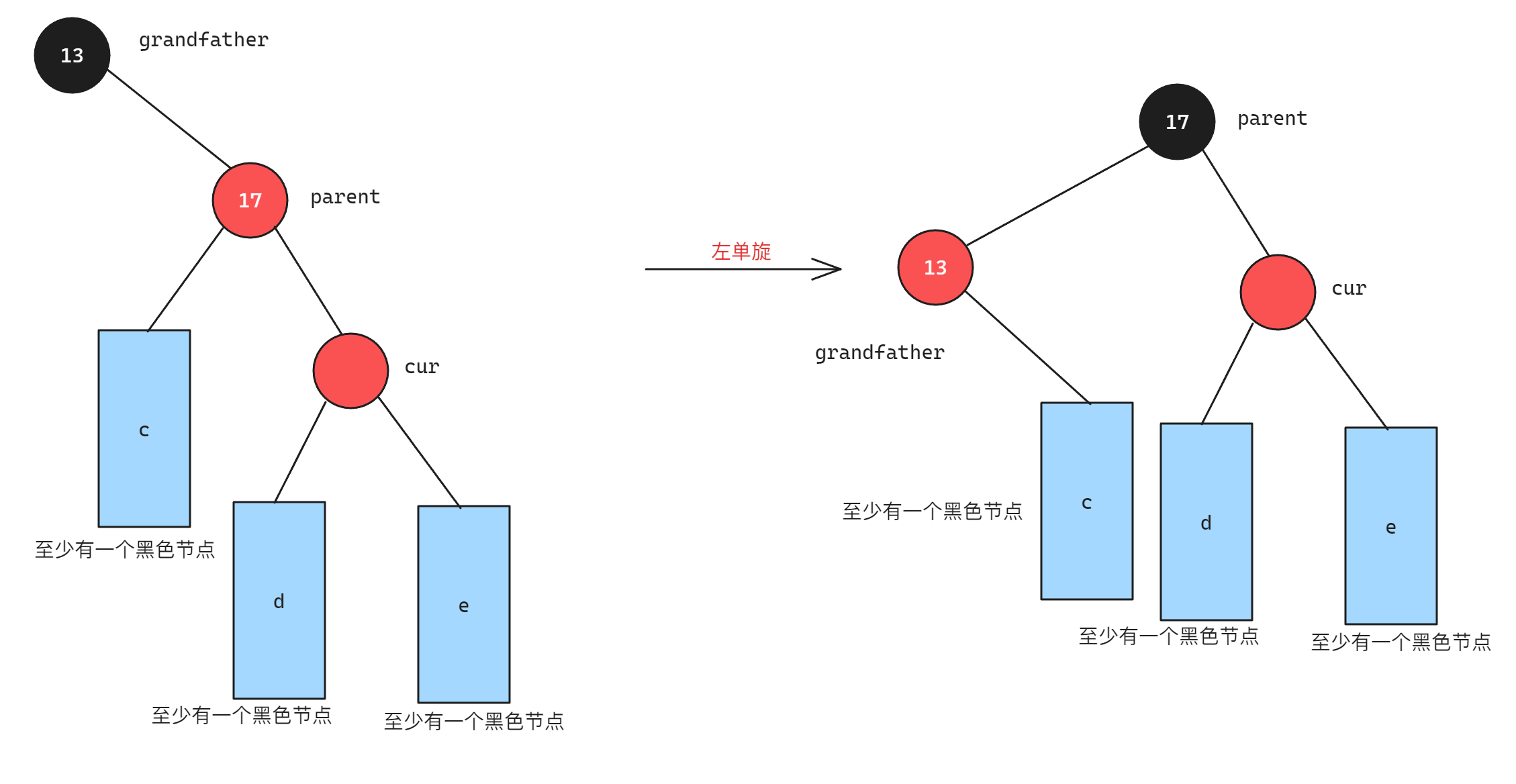
当cur节点在parent的左子树并且parent在grandfather的左子树时，此时需要进行右单旋，将parent的颜色更新为黑色，grandfather的颜色更新为红色，原因类比左单旋，过程如下图所示：

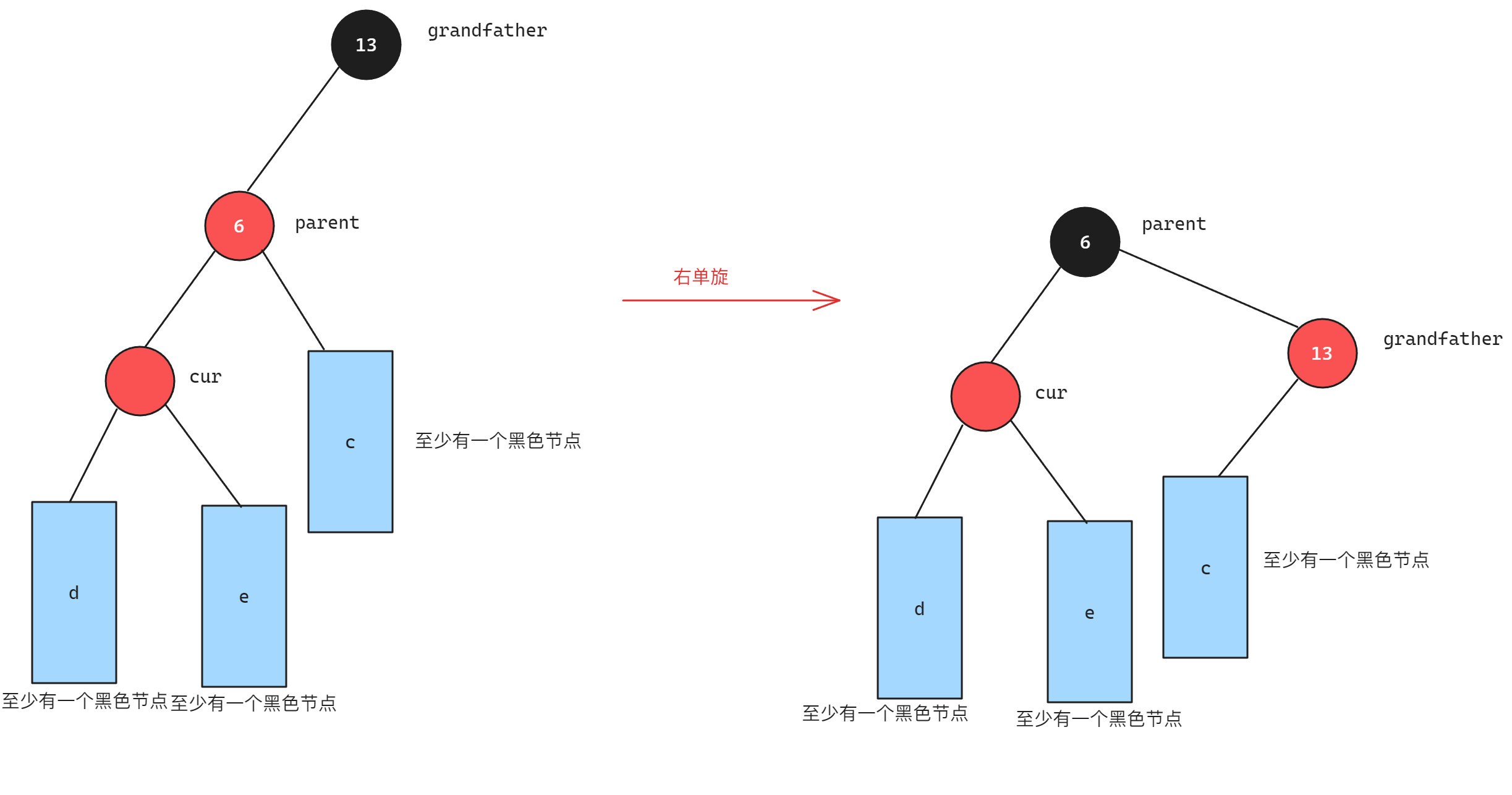
当cur节点在parent的右子树并且parent在grandfather的左子树时，此时需要进行右左双旋，将cur的颜色更新为黑色，将grandfather的颜色更新为红色，过程如下：

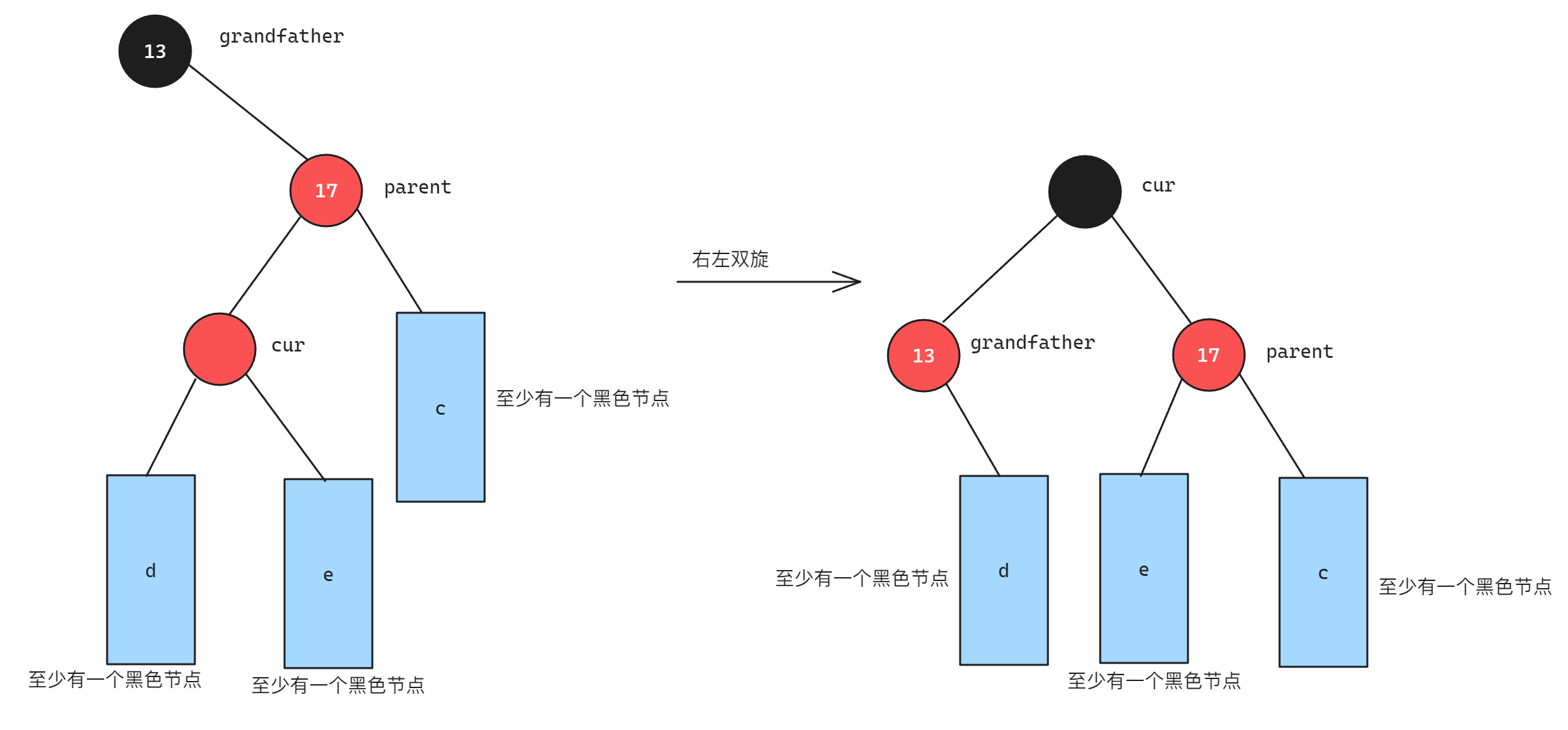
当cur节点在parent的左子树并且parent在grandfather的右子树时，此时需要进行左右双旋，将cur的颜色更新为黑色，将grandfather的颜色更新为红色，过程如下：

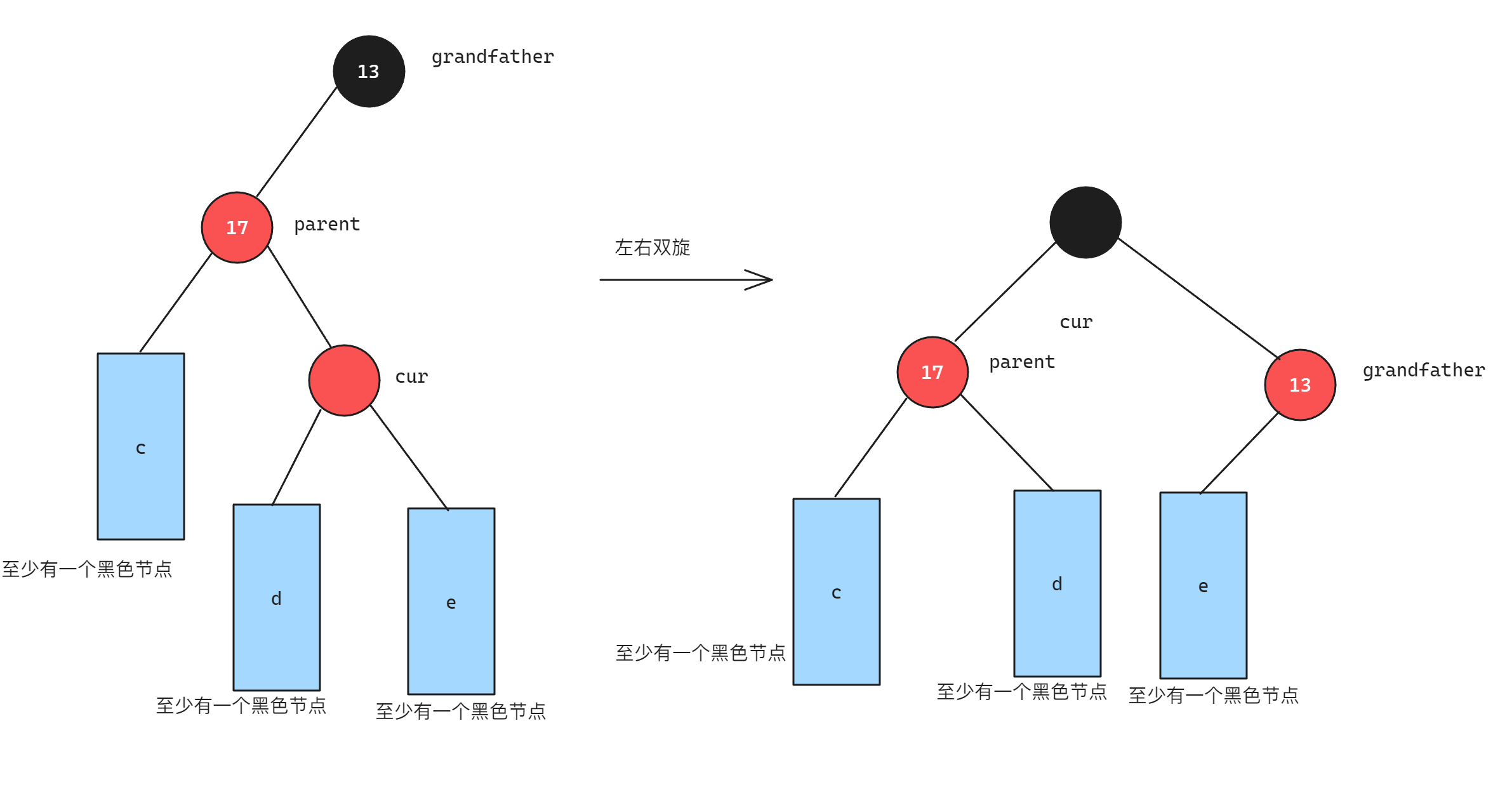
如果uncle节点本身存在，那么经过uncle节点的路径下方的两个子树为红色，而parent插入节点前至少会有一个黑色节点，如下图所示：

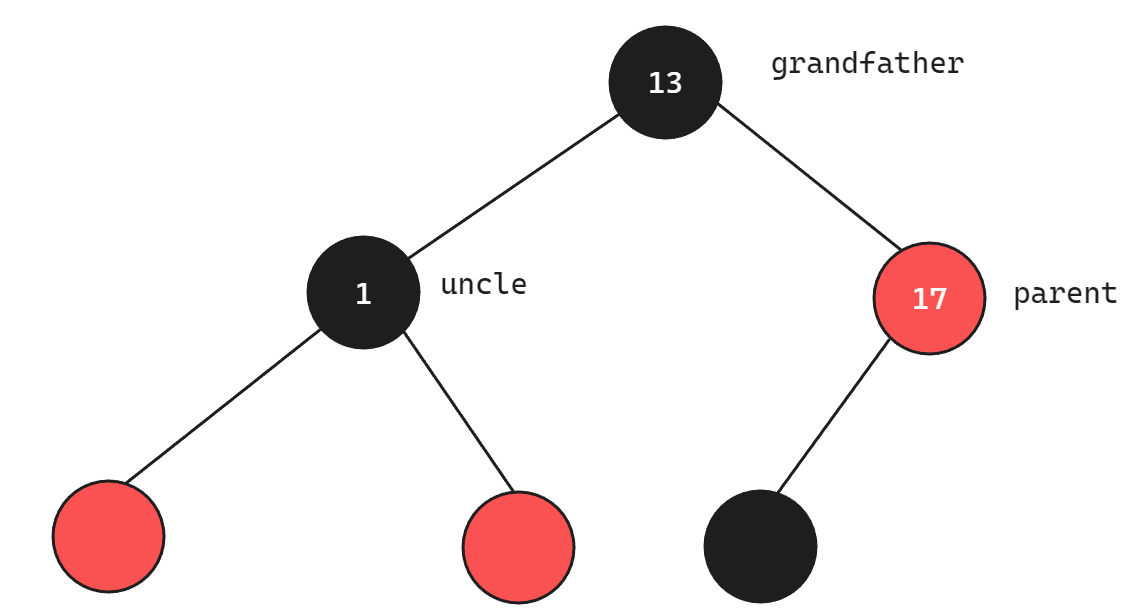
此时在parent的右侧插入一个cur节点（本身就是红色节点cur节点也是如此）如下：

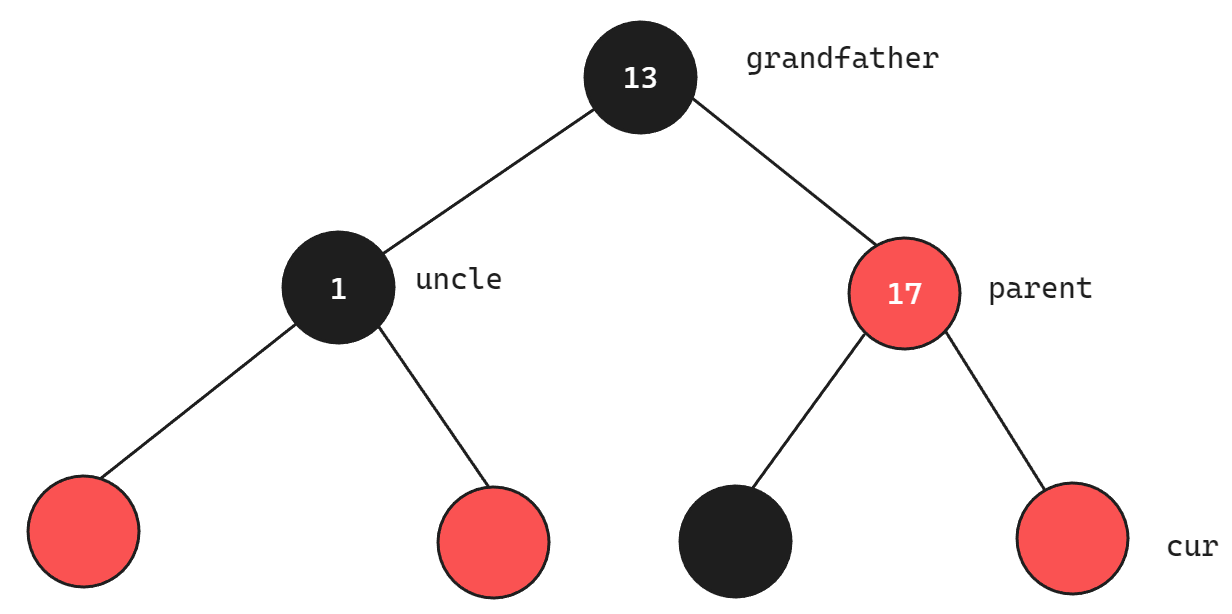
此时如果只是对parent节点的颜色进行改变，则会出现parent所在路径比uncle所在路径多一个黑色节点，所以为了解决这个问题，单单改变颜色无法解决，当cur在parent的右边时，只需要一次左单旋即可，而cur在parent的左边时，需要先进行右旋再进行左旋，以右左双旋为例，如下图所示：

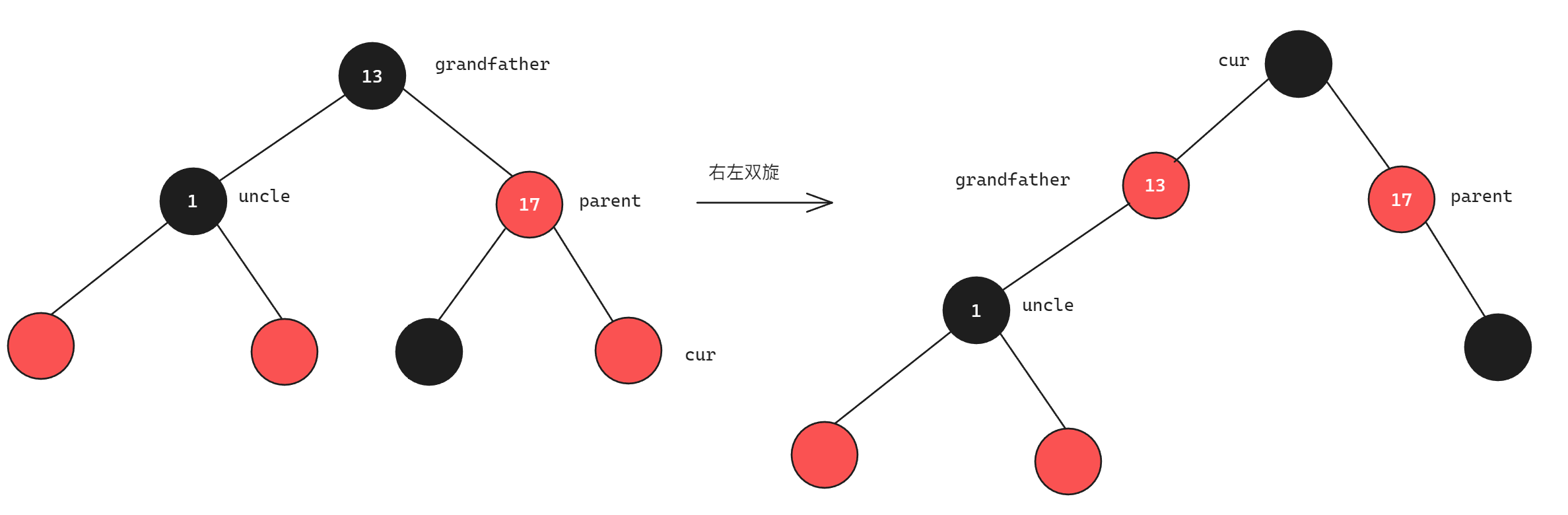
对于其他两种情况也是一样的道理，此处不再赘述

总结与代码实现

红黑树的插入过程一共有三种情况：

1. 当插入节点的父亲节点为黑色时，直接插入节点即可，不需要进行任何调整
2. 当uncle节点为红色时，cur节点的parent节点和uncle节点均变为黑色，将所在子树的根节点变为红色，如果子树的根节点为整棵树的根节点，则再处理为黑色
3. 当uncle节点为黑色（包括空节点的黑色和存在且为黑色节点）时，需要进行旋转
   1. parent和cur节点是同方向时，进行一次旋转（左旋或者右旋），将parent节点变为黑色，将grandfather节点变为红色，此时因为parent是本棵子树的根，所以更新完后当前子树也是一棵红黑树，颜色是黑色不需要再进行调整
   2. parent和cur节点不是同方向时，进行两次旋转（先左后右或者先右后左），再将cur节点变为黑色，grandfather节点变为红色，更新完后当前子树也是一棵红黑树，并且因为cur的颜色是黑色不需要再进行调整

代码实现：

// 树插入
bool insertNode(const pair<T, V>& kv)
{// 判断key是否已经存在if (findNode(kv.first)){// 已经存在时插入失败return false;}// 判断根节点是否为空，为空则作为第一个节点if (_root == nullptr){_root = new node(kv);return true;}// 根节点不为空时接着遍历插入node* cur = _root;// 定义父亲节点记录父亲的位置node* parent = _root;while (cur){if (kv.first > cur->_kv.first){// 大于根节点数据，插入在右子树，走到左子树的空位置parent = cur;cur = cur->_right;}else if (kv.first < cur->_kv.first){// 小于根节点数据，插入在左子树，走到右子树的空位置parent = cur;cur = cur->_left;}}// 创建node节点// 创建节点可以使用新节点，但是要使cur走到新节点的位置，便于下面判断新节点的平衡因子，再通过cur判断祖先节点的平衡因子cur = new node(kv);// parent为叶子节点，链接新节点if (parent->_kv.first < kv.first){// 如果是右子树，则插入在右子树parent->_right = cur;}else{// 否则插入在左子树parent->_left = cur;}// 链接父亲cur->_parent = parent;// 插入节点颜色为红色cur->_col = Red;// 存在父亲且当父亲节点为红色时需要判断是否更新while (parent && parent->_parent && parent->_col == Red){node* grandfather = parent->_parent;if (grandfather->_right == parent){node* uncle = grandfather->_left;if (uncle && uncle->_col == Red){// 叔叔存在且为红uncle->_col = parent->_col = Black;grandfather->_col = Red;cur = grandfather;parent = cur->_parent;}else{// cur在parent的右孩子if (cur == parent->_right){// 右右->左单旋rotateLeft(grandfather);// 改变颜色grandfather->_col = Red;parent->_col = Black;}else{// 右左->右左双旋rotateRight(parent);rotateLeft(grandfather);cur->_col = Black;grandfather->_col = Red;}// 旋转结束后不需要再向上更新break;}}else{node* uncle = grandfather->_right;if (uncle && uncle->_col == Red){// 叔叔存在且为红uncle->_col = parent->_col = Black;grandfather->_col = Red;// 继续向上更新cur = grandfather;parent = cur->_parent;}else{if(cur == parent->_left){// 叔叔不存在// 左左->右单旋rotateRight(grandfather);// 改变颜色grandfather->_col = Red;parent->_col = Black;}else{// 左右->左右双旋rotateLeft(parent);rotateRight(grandfather);// 改变颜色grandfather->_col = Red;cur->_col = Black;}// 旋转结束后不需要再向上更新break;}}}// 根节点为黑色_root->_col = Black;return true;
}

红黑树的删除（待实现）

红黑树的效率

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O()，红黑树不追

求绝对平衡，其只需保证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，

所以在经常进行增删的结构中性能比AVL树更优，而且红黑树实现比较简单，所以实际运用中红

黑树更多