LeetCode LCR147.最小栈

LeetCode LCR147.最小栈

思路🤔：

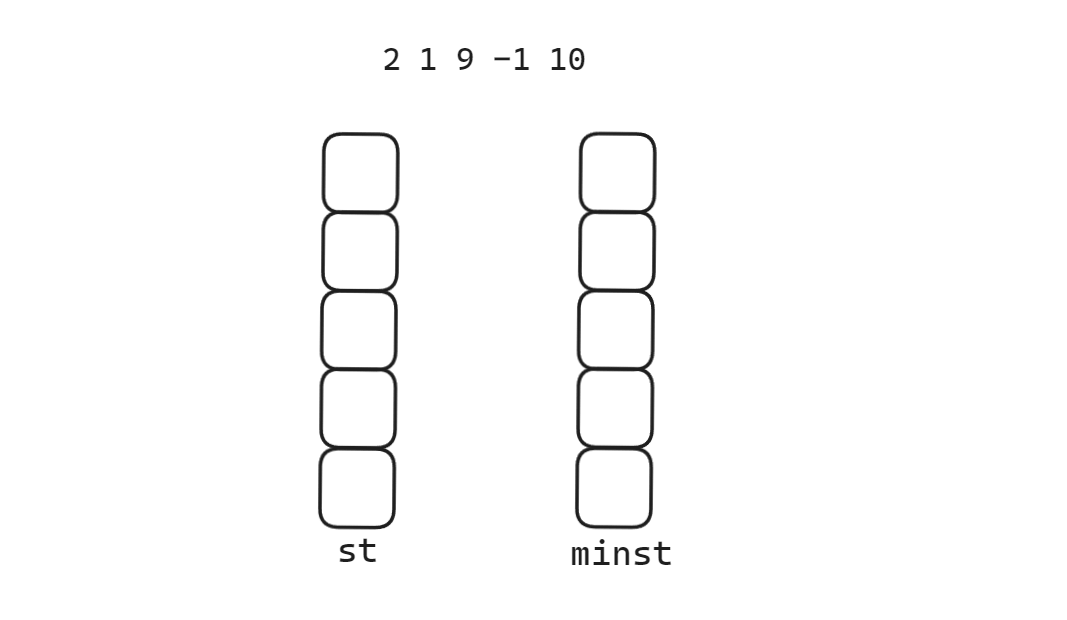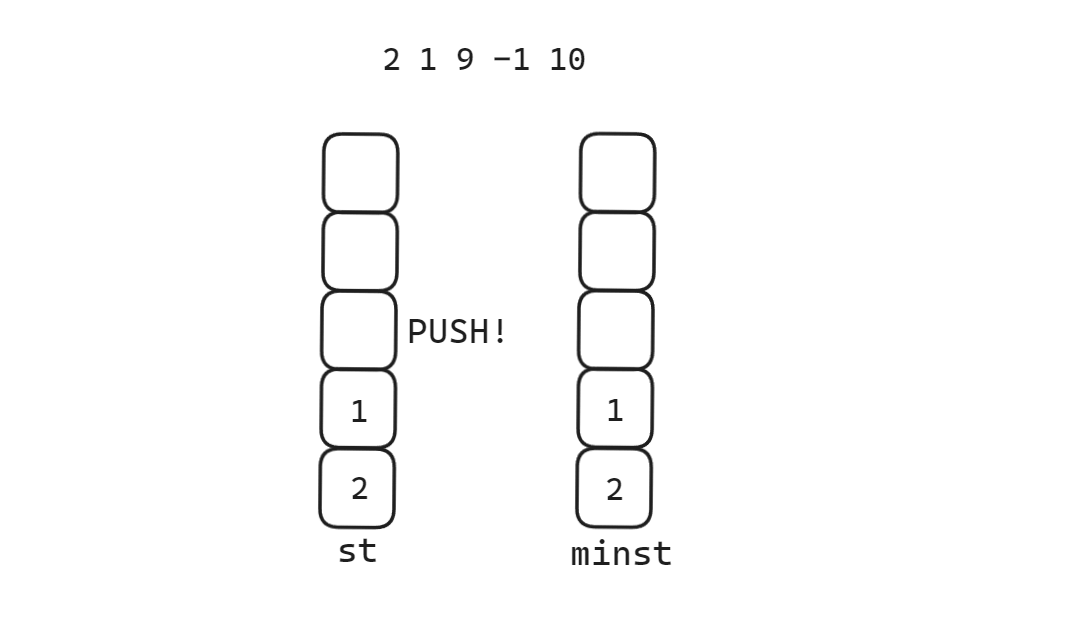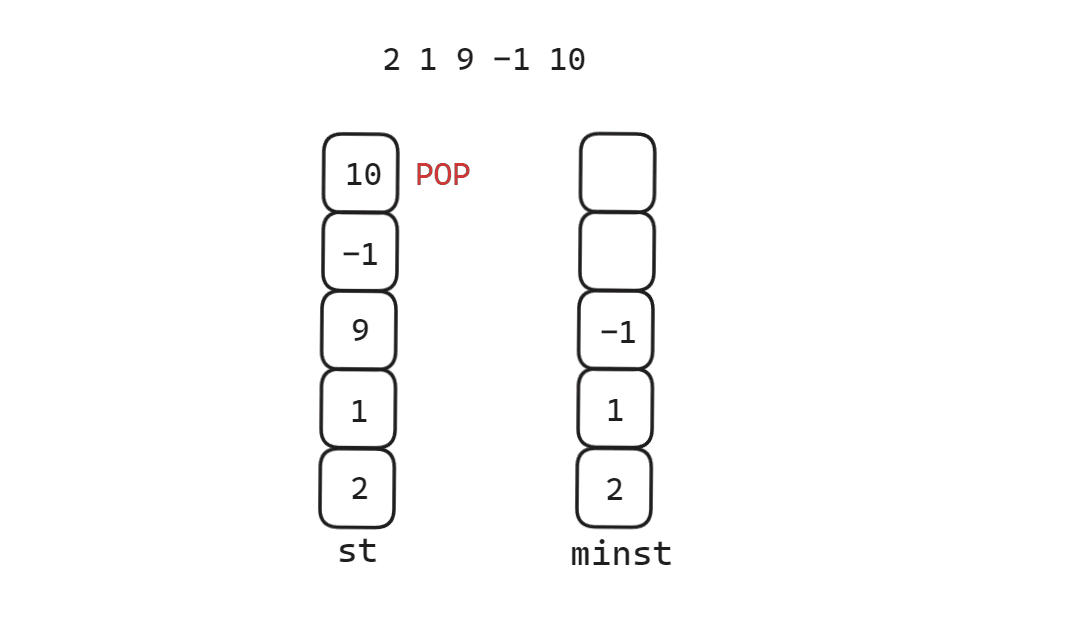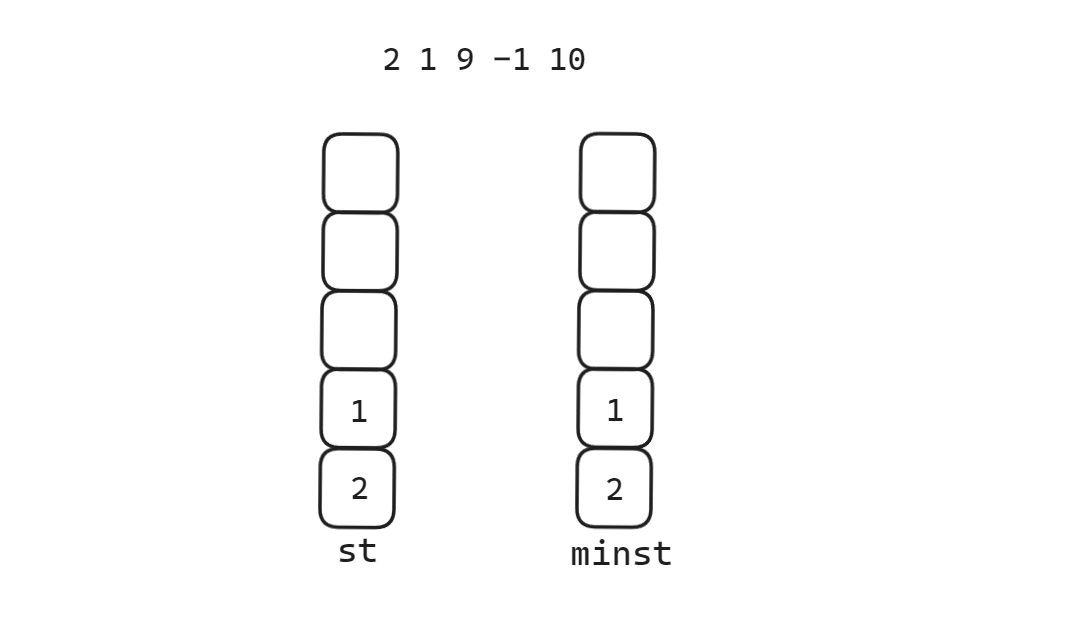
  建立两个栈，一个栈正常入栈出栈，一个栈只用于出入最小数，当push值小于minst栈顶才入栈，当pop值等于minst栈顶才出栈。

代码🔎：

class MinStack {
public:MinStack() {//自定义类型编译器会去调用相关构造}void push(int x) {_st.push(x);if(_minst.empty() || x <= _minst.top()) //如果更小就push，如果最小栈为空就先入一个{_minst.push(x);}}void pop() {if(_st.top() == _minst.top()) //出栈值跟最小栈元素一样才一起出{_minst.pop();}_st.pop();}int top() {return _st.top(); //正常栈返回即可}int getMin() {return _minst.top(); //最小栈返回}stack<int> _st;stack<int> _minst;
};