人工智能深度学习系列—深度学习中的相似性追求:Triplet Loss 全解析
人工智能深度学习系列—深度解析:交叉熵损失(Cross-Entropy Loss)在分类问题中的应用
人工智能深度学习系列—深入解析:均方误差损失(MSE Loss)在深度学习中的应用与实践
人工智能深度学习系列—深入探索KL散度:度量概率分布差异的关键工具
人工智能深度学习系列—探索余弦相似度损失:深度学习中的相似性度量神器
人工智能深度学习系列—深度学习中的边界框回归新贵:GHM(Generalized Histogram Loss)全解析
人工智能深度学习系列—深度学习损失函数中的Focal Loss解析
人工智能深度学习系列—Wasserstein Loss:度量概率分布差异的新视角
人工智能深度学习系列—GANs的对抗博弈:深入解析Adversarial Loss
人工智能深度学习系列—探索Jaccard相似度损失:图像分割领域的新利器
人工智能深度学习系列—深入探索IoU Loss及其变种:目标检测与分割的精度优化利器
人工智能深度学习系列—深度学习中的相似性追求:Triplet Loss 全解析
文章目录
- 1. 背景介绍
- 2. Loss计算公式
- 3. 使用场景
- 4. 代码样例
- 5. 总结
1. 背景介绍
在机器学习和模式识别领域,相似性度量是核心问题之一。Triplet Loss,作为一种特殊的损失函数,被设计用来学习数据的相对距离,从而使得相似样本更接近,不同样本更疏远。本文将详细介绍Triplet Loss的背景、计算方法、使用场景、代码实现及总结。
Triplet Loss最早由Schroff等人在2015年提出,用于改进深度学习中的度量学习任务。它通过同时考虑三个样本点:锚点(anchor)、正样本(positive)和负样本(negative),来构建损失函数,使得锚点与正样本的距离小于锚点与负样本的距离。

2. Loss计算公式
Triplet Loss的计算公式如下:
L = ∑ i = 1 N max ( 0 , d ( a i , p i ) − d ( a i , n i ) + m a r g i n ) L = \sum_{i=1}^{N} \max(0, d(a_i, p_i) - d(a_i, n_i) + margin) L=∑i=1Nmax(0,d(ai,pi)−d(ai,ni)+margin)
其中:
- a i a_i ai是锚点样本的特征表示。
- p i p_i pi是与锚点相同类别的正样本。
- n i n_i ni是与锚点不同类别的负样本。
- d d d是样本特征之间的距离度量,通常使用欧氏距离或余弦相似度。
- m a r g i n margin margin是正负样本对之间需要保持的最小距离。
3. 使用场景
Triplet Loss由于其独特的设计,在多个领域和应用中发挥着重要作用,以下是对其使用场景的扩展描述:
-
度量学习(Metric Learning)
- 在度量学习中,Triplet Loss通过优化特征空间,使得相同类别的样本在该空间中更接近,而不同类别的样本更疏远。这种方法广泛应用于各种基于内容的检索系统,如基于图像的图像检索(CBIR)。
-
人脸识别(Face Recognition)
- 人脸识别系统依赖于精确的特征表示来区分不同的个体。Triplet Loss通过确保来自同一人脸的特征向量比来自不同人脸的特征向量更接近,从而提高系统的识别能力和鲁棒性。
-
相似性搜索(Similarity Search)
- 在商品推荐系统中,Triplet Loss有助于学习商品的特征表示,使得系统能够推荐与用户兴趣更相似的商品。在图像检索中,它确保了检索结果与查询图像在视觉特征上的相似性。
-
签名验证(Signature Verification)
- 签名验证系统需要识别签名的细微差别和个人特有的笔迹模式。Triplet Loss可以强化模型对这些细微差别的敏感性,提高伪造签名的检测能力。
-
推荐系统(Recommendation Systems)
- 在推荐系统中,Triplet Loss可以用于优化用户和物品之间的相似性度量,从而提供更个性化的推荐列表,增强用户体验。
-
情感分析(Sentiment Analysis)
- 在情感分析中,Triplet Loss可以用来学习文本的情感倾向表示,使得具有相同情感的文本样本在特征空间中更接近,有助于提高情感分类的准确性。
-
医学图像分析(Medical Image Analysis)
- 在医学图像分析领域,Triplet Loss有助于从图像中学习病变的特征表示,使得相同类型的病变样本更相似,不同类型则更疏远,这对于辅助诊断和病情评估非常有用。
-
视频监控(Video Surveillance)
- 在视频监控系统中,Triplet Loss可以用于学习不同帧中目标的特征表示,以便于跟踪和识别同一目标,即使在目标外观发生变化的情况下。
-
语音识别(Speech Recognition)
- 在自动语音识别中,Triplet Loss有助于优化声学特征的表示,使得相同发音的特征向量更接近,不同发音的特征向量更疏远,从而提高识别的准确度。
-
多模态学习(Multimodal Learning)
- 在多模态学习中,Triplet Loss可以用于学习跨模态的一致性特征表示,使得来自不同模态但相同概念的特征向量在特征空间中更接近。
通过这些应用场景,我们可以看到Triplet Loss在需要学习样本间相对距离和相似性度量的任务中具有广泛的应用潜力。随着深度学习技术的不断发展,Triplet Loss预计将在未来的应用中发挥更大的作用。
4. 代码样例
以下是使用Python和PyTorch库实现Triplet Loss的示例代码:
import torch
import torch.nn as nn
import torch.nn.functional as Fclass TripletLoss(nn.Module):def __init__(self, margin=1.0):super(TripletLoss, self).__init__()self.margin = margindef forward(self, anchor, positive, negative):d_pos = F.pairwise_distance(anchor, positive)d_neg = F.pairwise_distance(anchor, negative)loss = torch.clamp(self.margin + d_pos - d_neg, min=0)return loss.mean()# 假设有一些特征向量
anchor = torch.randn(10, 128) # 锚点特征
positive = torch.randn(10, 128) # 正样本特征
negative = torch.randn(10, 128) # 负样本特征# 实例化TripletLoss并计算损失
triplet_loss = TripletLoss(margin=1.0)
loss = triplet_loss(anchor, positive, negative)
print("Triplet Loss:", loss.item())# 反向传播
loss.backward()
5. 总结
Triplet Loss作为一种有效的相似性度量学习工具,在需要学习样本间相对距离的场景中具有显著的优势。通过本文的介绍,希望能够帮助CSDN社区的读者深入理解Triplet Loss,并在实际项目中有效应用。

相关文章:

人工智能深度学习系列—深度学习中的相似性追求:Triplet Loss 全解析
人工智能深度学习系列—深度解析:交叉熵损失(Cross-Entropy Loss)在分类问题中的应用 人工智能深度学习系列—深入解析:均方误差损失(MSE Loss)在深度学习中的应用与实践 人工智能深度学习系列—深入探索KL…...

26. Hibernate 如何自动生成 SQL 语句
1. 前言 本节和大家一起聊聊 Hibernate 是如何自动生成 SQL 语句的。通过本节的学习,你将了解到: 反射在框架中的重要性;元数据描述对 Hibernate 的重要性。 2. 理想状态 Hibernate 是全自动的 JDBC 框架,能自动构建 SQL 语句、…...
)
预言机(Oracle machine)
预言机(Oracle machine)是一个在多个领域中有不同应用和解释的概念。以下是从不同角度对预言机的详细解析: 一、计算复杂度理论与可计算性理论中的预言机 在计算复杂度理论与可计算性理论中,预言机是一种抽象电脑,用…...

55、PHP实现插入排序、二分查找
题目: PHP实现插入排序 描述: 思路:选择一个带插入的元素(假设从第一个开始),分别和已经插入有顺序的元素比较,如果要插入元素比比较元素小,则位置交换 function insertSort($arr){if(!is_array($arr)) return false;//外层循环插入次数for($i1;$i<…...

[Git][分支设计规范]详细讲解
目录 0.概览1.master分支2.release分支3.develop分支4.feature分支5.hotfix分支 0.概览 以下是常用的分支和环境的搭配,可视情况而定不同的策略 分支名称适用环境master主分支生产环境release预发布分支预发布/测试环境develop开发分支开发环境feature需求开发分支本…...

c#中winfrom需要了解的
如何用代码实现label1的字体大小 方法1:在设计视图中设置 打开你的Windows Forms项目。 在设计视图中,选中你想要更改字体大小的Label控件。 在属性窗口中,找到Font属性,点击旁边的省略号(...)。 在弹出的字体对话框中&#x…...
操作系统03:调度算法和文件系统
文章目录 调度算法进程调度算法先来先服务调度算法最短作业优先调度算法高响应比优先调度算法时间片轮转调度算法最高优先级调度算法 内存页面置换算法最佳页面置换算法(OPT)先进先出置换算法(FIFO)最近最久未使用的置换算法&…...
大量中国高清地图,必须收藏!!
1、中国人口密度 2、中国干湿区 3、中国温度带和干湿状况 4、中国气温分布 5、中国高陆状况 6、国家级高新技术产业开发区 7、中国工业布局的变化 8、中国旱灾 9、中国常年河与时令河 10、中国科斯塔地貌分布图 11、中国泥石流、滑坡崩塌灾害分布 12、中国森林和主要牧区分布图…...

无线领夹麦克风哪个品牌好,2024年收音麦哪个品牌好一点
在自媒体的浪潮中,内容创作者对于高质量音频的需求日益增长,这直接推动了无线领夹麦克风的兴起。过去,创作者们可能更倾向于使用传统的有线麦克风,但随着技术的进步和市场的变化,无线领夹麦克风以其便携性和灵活性的优…...

如何解决.NET8 类库Debug时,Debug文件夹中不包含Packages中引入的文件
最近在开发中使用了.NET8 Razor类库项目,但是惊讶的发现Debug时,Debug文件夹中不包含Packages中引入的文件,本以为是非常小的问题,但是被困住了竟然足足4个小时。 其实它也本就是个非常非常小的问题…… 只需引入<CopyLocalL…...

域名安全详解
域名安全是网络安全的重要组成部分,涉及多个方面。以下是域名安全的详细介绍: 1. 域名劫持防护 域名劫持是指攻击者通过各种手段,将用户访问的域名解析到非法IP地址上。 防护措施: 使用DNSSEC(域名系统安全扩展)定期监控域名解析记录选择可靠的域名注册商和DNS服务提供…...

使用gstreamer命令行解析RTSP流
1、解析成图片: gst-launch-1.0 rtspsrc locationrtsp://xxxx protocolstcp ! rtph264depay ! h264parse ! queue ! avdec_h264 ! videoconvert ! videorate ! videoscale ! videoconvert ! capsfilter capsvideo/x-raw,formatI420,width640,height480,framerate30…...
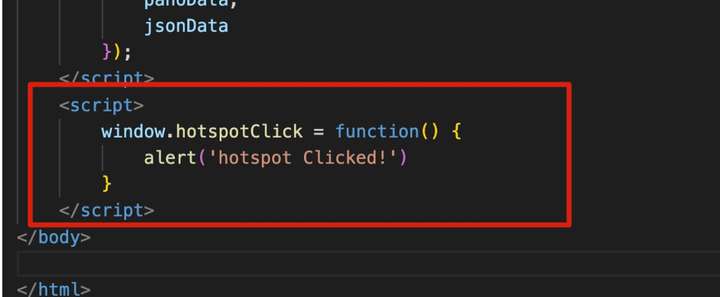
如何基于离线包中“事件热点”进行二次开发
720漫游支持基于作品离线包中的自定义按钮/热点-事件进行二次开发来实现与自己业务相关的扩展功能。 开发者可以基于离线包二次开发自定义设置点击热点图标需要执行什么操作?比如打开实时监控画面弹窗,调用自己后台的数据并弹窗显示等。 操作流程&…...

使用继电器实现门电路(1)常用门电路的简化实现
非门INC 常闭x1 反向输入信号 与门AND 常开x1 当A和B都为1时,O才为1,否则O为0。 或门OR 常开x1 当A和B中任意一个为1时,O为1,只有当A和B都为0时,O才为0。 或非门NOR 当A和B中任意一个为1时,O为0&…...

程序员常用单词分类
程序员在编程、软件开发、系统维护等工作中,会频繁使用到一系列特定的单词和术语。这些单词可以根据其功能、用途或所属领域进行分类。以下是一些常见的分类及其示例单词: 1. 数据类型与变量 数据类型:整型(Integer)…...

c语言11天笔记
函数的概述 函数:实现一定功能的,独立的代码模块。我们的函数一定是先定义,后使用。 使用函数的优势: 1. 我们可以通过函数提供功能给别人使用。当然我们也可以使用别人提供的函数,减少代码量。 2. 借助函数可以减…...

【C++刷题】优选算法——贪心第三辑
坏了的计算器 int brokenCalc(int startValue, int target) {int step 0;while (target > startValue) {if (target % 2 0) target / 2;else target 1;step;}return step startValue - target; }合并区间 区间问题,先排序 vector<vector<int>>…...

9.2 grafana 上导入模板看图并讲解告警
本节重点介绍 : 添加到prometheus采集配置中grafana 上导入process-exporter dashboard重点指标讲解 添加到prometheus采集配置中 - job_name: process-exporterhonor_timestamps: truescrape_interval: 15sscrape_timeout: 10smetrics_path: /metricsscheme: httpstatic_con…...

python实现自动回复消息
本文使用创作助手。 下面是一个使用uiautomation库实现自动回复QQ消息的示例代码: import time import uiautomation as autodef auto_reply():# 打开QQauto.uiautomationhelper.ShellExecute(r"C:\Program Files (x86)\Tencent\QQ\Bin\QQScLauncher.exe&quo…...

Mysql 脚本转换为drawio ER 脚本
Navicat 导出数据库脚本 通过代码转换脚本 import java.io.BufferedReader; import java.io.FileReader; import java.io.FileWriter; import java.io.IOException; import java.util.regex.Matcher; import java.util.regex.Pattern;/*** SQL 脚本转换为 drawio ER 脚本*/ pu…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...
