【Python机器学习】回归——缩减系数来“理解”数据
如果数据特征比样本点还多,是不可以使用线性回归的,因为在计算的时候会出错。
如果特征比样本点还多(n>m),也就是说输入数据的矩阵x不是满秩矩阵。非满秩矩阵在求逆时会出问题。
为了解决上述问题,可以使用岭回归,接着是lasso法,该方法效果很好但是计算复杂。还有前向逐步回归,可以得到与lasso相似的效果,且更容易实现。
岭回归
简单来说,岭回归就是在矩阵上加一个
从而使得矩阵非奇异,进而能对
+
求逆。其中矩阵I是一个m*m的单位矩阵,对角线上元素全是1,其他元素全为0。而
是一个用户定义的数值。在这种情况下,回归系数的计算公式将变成:
岭回归最先用来处理特征数多余样本数的情况,现在也用于子啊估计中加入偏差,从而得到更好的估计。这里通过引入来限制了所有w之和,通过引入该惩罚项,能够减少不必要的参数,这个技术在统计学中也叫做缩减。
缩减方法可以去掉不重要的参数,因此能更好地理解数据。此外,和简单的线性回归相比,错减法能取得更好的预测效果。
与之前用到的训练其他参数所用方法类似,通过预测误差最小化得到:数据获取之后,首先抽一部分数据用于测试,剩余的作为训练集用于训练参数w。训练完毕后再测试集上测试预测性能。通过选取不同的
来重复上述测试过程,最终得到一个使预测误差最小的
。
岭回归代码实现:
def ridgeRegres(xMat,yMat,lam=0.2):xTx=xMat.T*xMatdenom=xTx+eye(shape(xMat)[1])*lamif linalg.det(denom)==0.0:print('行列式为0')return ws=denom.I*(xMat.T*yMat)return wsdef ridgeTest(xArr,yArr):xMat=mat(xArr)yMat=mat(yArr).TyMean=mean(yMat,0)yMat=yMat-yMeanxMeans=mean(xMat,0)xVar=var(xMat,0)xMat=(xMat-xMeans)/xVarnumTestPets=30wMat=zeros((numTestPets,shape(xMat)[1]))for i in range(numTestPets):ws=ridgeRegres(xMat,yMat,exp(i-10))wMat[i,:]=ws.Treturn wMat上述代码包含两个函数:ridgeRegres()用于计算回归系数,而函数ridgeTest()用于在一组上测试结果。
第一个函数ridgeRegres()实现了给定lambda下的岭回归求解。如果没有指定lambda,则默认为0.2。由于lambda是Python保留的关键字,所以代码中用lam代替。函数首先构建矩阵,然后用lam乘以单位矩阵。在普通回归方法可能会产生错误时,岭回归仍然可以正常工作。这里需要做一个检查。最后,如果矩阵非奇异就计算回归系数并返回。
为了使用岭回归和缩减技术,首先需要对特征做标准化处理,使每维特征具有相同的重要性。ridgeRegres()展示了数据标准化过程。具体的做法就是所有特征都减去各自的均值并除以方差。
处理完成后就可以在30个不同lambda下调用ridgeRegres()函数。这里的lambda应该以指数级变化,这样可以看出lambda在取非常小的值时和取非常大的值时分别对结果造成的影响。最后将所有的回归系数输出到一个矩阵并返回。
尝试在鲍鱼数据集上运行:
abX,abY=loadDataSet('abalone.txt')
ridgeWeights=ridgeTest(abX,abY)
import matplotlib.pyplot as plt
fig=plt.figure()
ax=fig.add_subplot(111)
ax.plot(ridgeWeights)
plt.show()
上图绘制出了回归系数与的关系。在最左边,即
最小时,可以得到所有系数的原始值(与线性回归一致),而在右边,系数全都缩减为0;在中间部分的某值将可以取得最好的预测效果。为了定量的找到最佳参数值,还需要进行交叉验证。另外还要判断哪些变量对结果预测最具有影响力。
lasso
不难证明,在增加下面的约束时,普通的最小二乘法回归会得到与岭回归一样的公式:
上面的表达式限定了所有回归系数的平方和不能大于。使用最小二乘法回归在当两个或更多的特征相关时,可能会得出一个很大的正系数和一个很大的负系数。正式因为上述限制条件的存在,使得岭回归可以避免这个问题。
与岭回归类似,另一个缩减方法lasso也对回归系数做了限定,限定条件如下:
唯一不同的点在于:这个约束条件用绝对值代替了平方和。虽然约束形式只是稍作变化,结果却完全不同:在足够小的时候,一些系数会因此被迫缩减到0,这个特性可以帮助我们更好地理解数据。这两个约束条件在看起来相差无几,但是极大地增加了计算复杂度。
前向逐步回归
前向逐步回归算法可以得到与lasso差不多的效果,但更简单。它属于一种贪心算法,即每一步都尽可能减少误差。一开始,所有的权重都设置为1,然后每一步所做的决策是对某个权重增加或者减少到一个很小的值。
该算法的伪代码如下:
数据标准化,使其分布满足0均值和单位方差
在每轮迭代过程中:
设置当前最小误差lowestError为正无穷
对每个特征:
增大或缩小:
改变一个系数得到一个新的w
计算新w下的误差
如果误差Error小于当前最小误差lowestError:设置Wbest等于当前的W
将w设置为新的Wbest
实际代码实现:
def stageWise(xArr,yArr,eps=0.01,numIt=100):#转换数据并存入矩阵xMat=mat(xArr)yMat=mat(yArr).TyMean=mean(yMat,0)yMat=yMat-yMean#xMat=regularize(xMat)m,n=shape(xMat)returnMat=zeros((numIt,n))#创建向量ws来保存w的值ws=zeros((n,1))wsTest=ws.copy()wsMax=ws.copy()#循环numIt次,并且在每次迭代时都打印出w向量,用于分析算法执行的过程和效果for i in range(numIt):print(ws.T)lowestError=inffor j in range(n):for sign in [-1,1]:wsTest=ws.copy()wsTest[j]=wsTest[j]+eps*signyTest=xMat*wsTestrssE=rssError(yMat.A,yTest.A)if rssE<lowestError:lowestError=rssEwsMax=wsTestws=wsMax.copy()returnMat[i,:]=ws.Treturn returnMat上述stageWise()是一个逐步线性回归算法的实现,它与lasso做法相近但计算简单。该函数的输入包括:输入数据xArr和预测变量yArr。此外还有两个参数:一个是eps,表示每次迭代需要调整的步长;另一个是numIt,表示迭代次数。
函数首先将输入数据转换并存入矩阵中,然后把特征按照均值为0方差为1进行标准化处理。在这之后创建了一个向量ws来保存w的值,并且为了实现贪心算法建立了ws的两份副本。接下来的优化过程需要迭代numIt次,并且在每次迭代时都打印出w向量,用于分析算法执行的过程和效果。
贪心算法在所有特征上运行两次for循环,分别计算增加或减少该特征对误差的影响。这里使用的是平方误差,通过之前的函数rssError()得到。该误差初始值设为正无穷,经过与所有的误差比较后取最小的误差,整个过程循环迭代进行。
xArr,yArr=loadDataSet('abalone.txt')
print(stageWise(xArr,yArr,0.01,200))

上述结果中,w1和w6都是0,表示他们不对目标值造成任何影响,也就是说这些特征很可能是不需要的。另外,在参数eps设置为0.01时,一段时间后系数就已经饱和并在特定值之间来回震荡,这是因为步长太大的缘故。
xMat=mat(xArr)
yMat=mat(yArr).T
yM=mean(yMat,0)
yMat=yMat-yM
weights=standRegres(xMat,yMat.T)
print(weights.T)
逐步线性回归算法的主要优点在于它可以帮助人们理解现有的模型并做出改进,当构建了一个模型后,可以运算该算法找出重要的特征,这样就有可能及时停止对那些不重要特征的收集。最后,如果用于测试,该算法每100次迭代后就可以构建出一个模型,可以使用类似于10折交叉验证的方法比较这些模型,最终选择使误差最小的模型。
当应用缩减方法(比如逐步线性回归或岭回归)时,模型也就增加了偏差,与此同时却减小了模型的方差。
相关文章:

【Python机器学习】回归——缩减系数来“理解”数据
如果数据特征比样本点还多,是不可以使用线性回归的,因为在计算的时候会出错。 如果特征比样本点还多(n>m),也就是说输入数据的矩阵x不是满秩矩阵。非满秩矩阵在求逆时会出问题。 为了解决上述问题,可以…...

组件设计原则
state数据结构设计 用数据描述所有内容数据要结构化,易于程序操作(遍历、查找)数据要可扩展,以便增加新的功能 组件设计组件通讯 从功能上拆分层次尽量让组件原子化容器组件(只管理数据)& UI组件&am…...

简单搭建vue项目
1.先安装node.js和vite,具体参考: 2.管理员身份运行cmd,跳转到node安装目录: 输入: npm create vitelatest 输入项目名称,选择vue和JavaScript 2.VisualStudioCode打开(可能需要管理员权限)创建的文件夹,点…...
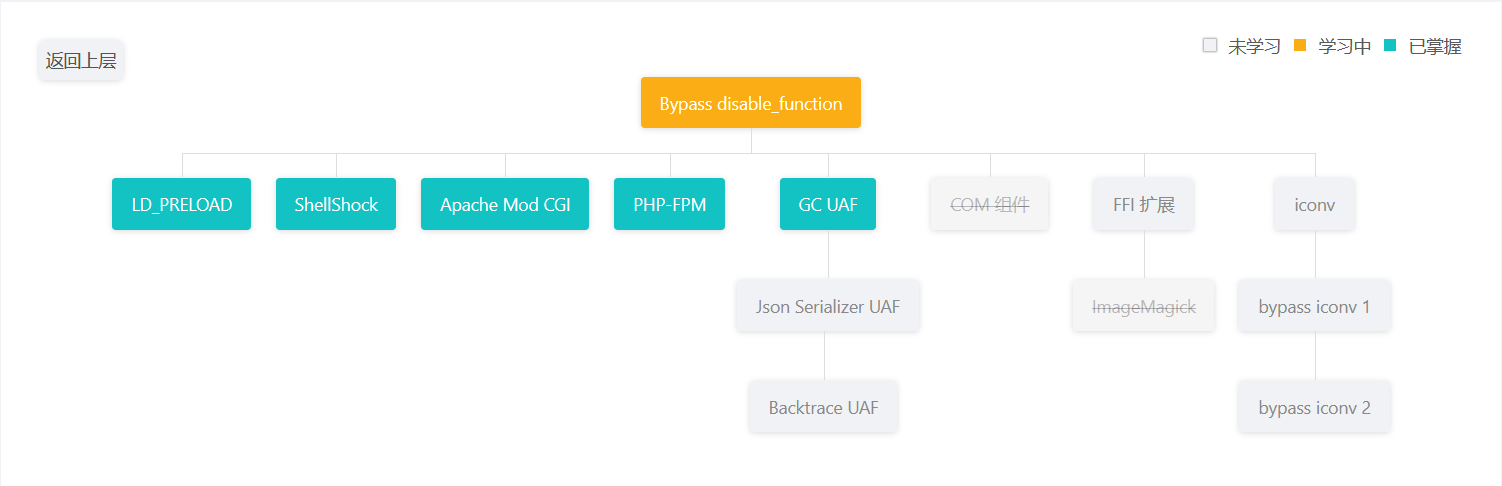
ctfhub Bypass disable_function
LD_PRELOAD url 蚁剑连接 选择插件 点击开始 查看到此文件名编辑连接拼接到url后面重新连接 点击开启终端 在终端执行命令 ls / /readfile ShellShock url CTFHub 环境实例 | 提示信息 蚁剑连接 写入shell.php <?phpeval($_REQUEST[ant]);putenv("PHP_test() { :…...

【Qt】探索Qt网络编程:构建高效通信应用
文章目录 前言:1. Qt 网络编程介绍1.1 什么是网络编程?1.2 Qt的模块 2. UDP Socket2.1 核心 API 概述2.2 写一个带有界面的 Udp 回显服务器2.3 写一个带有界面的 Udp 客户端 3. TCP Socket3.1 核心 API 概述3.2 代码: 4. HTTP Client4.1 核心…...

【Android Studio】原生应用部署第三方插件(探针)
一、本地引入包流程 (一)本地引入包内容 (二)本地引入包操作步骤 将 【probe-android-sdk】目录里面所有的aar包复制到嵌码项目工程(App级别)的 libs 目录下 二、添加插件 (一)…...
)
嵌入式学习之路 15(C语言基础学习——指针操作一维字符型数组)
字符型数组的定义和初始化 char s[] "hello";:在栈上开辟空间并初始化。const char *p "hello";:指针 p 指向字符串常量区的 "hello",只能读取不能修改。 指针变量的类型确定 指针变量的类型由其所指向的数据…...

C++ STL专题 list的底层实现
目录 1.模拟实现list 2.节点模板讲解 3.迭代器模板讲解 3.1为什么template 有三个类型参数 (1).class T (2).class ref (3).class ptr 3.2 *重载 3.3 ->重载 3.4 前置和后置的重载 3.5 前置--和--后置的重载 3.6 和!的重载 4. list模板讲解 4.1 begin()函数 …...

【JavaEE】线程池
目录 前言 什么是线程池 线程池的优点 ThreadPollExecutor中的构造方法 corePoolSize && maximumPoolSize keepAliveTime && unit workQueue threadFactory 如何在java中使用线程池 1.创建线程池对象 2.调用submit添加任务 3.调用shutdown关闭线程池…...

lvs实战项目-dr模式实现
一、环境准备 主机名IP地址router eth0:172.25.254.100 eth1:192.168.0.100 clienteth0:172.25.254.200lvseth1:192.168.0.50web1web2 1、client配置 [rootclient ~]# cat /etc/NetworkManager/system-connections/eth0.nmconne…...
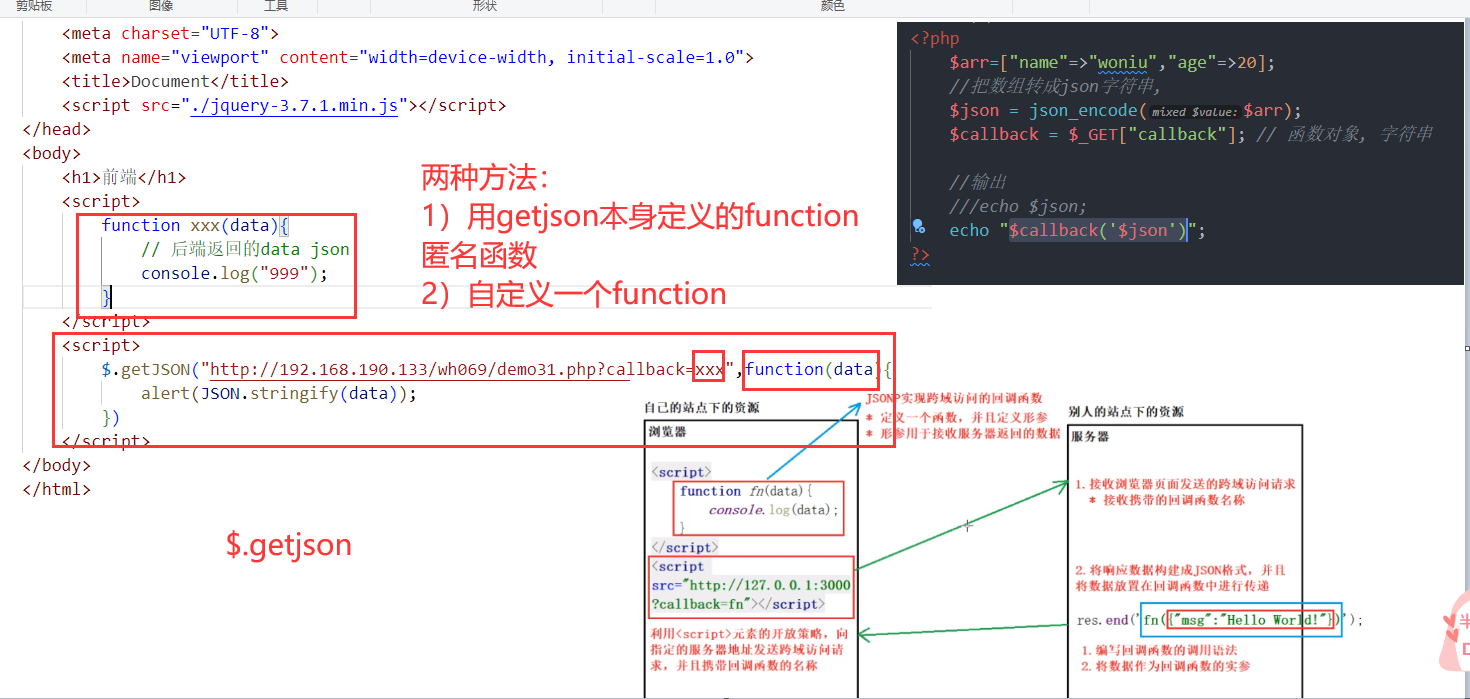
JSONP跨域
1 概述 定义 json存在的意义: 不同类型的语言,都能识别json JSONP(JSON with Padding)是JSON的一种“使用模式”,可用于解决主流浏览器的跨域数据访问的问题。由于同源策略,一般来说位于 server1.example.com 的网页无法与不是 s…...

Linux--shell脚本语言—/—终章
一、shell函数 1、shell函数定义格式 参数说明: 1、可以带function fun() 定义,也可以直接fun() 定义,不带任何参数。 2、参数返回,可以显示加:return 返回,如果不加,将以最后一条命令运行结果ÿ…...
免费代理池是什么,如何使用代理IP进行网络爬虫?
互联网是一个庞大的数据集合体,网络信息资源丰富且繁杂,想要从中找到自己需要的信息要花费较多的时间。为了解决这个问题,网络爬虫技术应运而生,它的主要作用就是在海量的互联网信息中进行爬取,抓取有效信息并存储。然…...

CAN直接网络管理(20240805)
长安CAN网络管理规范 个人理解:管理CAN网络中各NM节点的工作模式(状态); 1.术语定义 👉节点地址:用于唯一标识网络中每个节点的单字节数字,取值范围是 0x00~0xFF。👉状态迁移&#x…...

HTML5+CSS3笔记(Xmind格式):第二天
Xmind鸟瞰图: 简单文字总结: 新增选择器: 1.选择相邻兄弟 2.属性选择器 3.结构性伪类选择器 4.整体结构类型 5.标签结构类型 6.指定子元素的序号 7.文本选择伪元素 8.表单中使用的状态伪类选择器 9.内容…...

视频压缩文件太大了怎么缩小?6个视频压缩技巧,速度收藏起来!
高清视频文件,尤其是那些以 1080p 和 720p 清晰度为特征的视频,通常都拥有相当大的体积,会占据大量计算机存储空间。因此,为了更好地将它们进行分享和存储,您可能需要对它们进行压缩,以减小它们的尺寸。然而…...

Python接口自动化测试数据提取分析:Jmespath
1、引言 在处理JSON数据时,我们常常需要提取、筛选或者变换数据。手动编写这些操作的代码不仅繁琐,而且容易出错。Python作为一个功能强大的编程语言,拥有丰富的库和工具来处理这些数据。今天,将介绍一个实用的Python库——JMESP…...

特种设备作业叉车司机题库及答案
1.在我们平时工作中,经常接触的汽油、柴油、机油、油棉纱、木材等均为() A、助燃物质 B、可燃物质 C、着火源 参考答案:B 2.叉车满载行驶时,如合成重心靠后() A、有利于纵向稳定 B、有利于横向稳定 C、纵向和横向均有利 参考答案:A 3.蓄电池车行驶中放…...
Linux 操作系统速通
一、安装虚拟机 1. VmWare 安装下载 vmware workstation pro 16 下载 win R 输入 ncpa.cpl 确保网卡正常 2. CentOS 系统下载 CentOS 系统下载 将 CentOS 系统安装到虚拟机 3. 查看虚拟机 IP 命令 ifconfig 4. finalShell 安装下载 finalShell 下载 输入用户名一般是 ro…...

IIS漏洞大全(附修复方法)
IIS6.0 IlS Server 在 Web 服务扩展中开启了 WebDAV,配置了可以写入的权限,造成任意文件上传。 漏洞复现 fofa:"llS-6.0" or 本地搭建2003 server 1)开启 WebDAV 和写权限: 做好准备工作后开启环境,然后我们去访问配置的IP&#…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
