【算法】最短路径算法思路小结
一、基础:二叉树的遍历->图的遍历
提到搜索算法,就不得不说两个最基础的思想:
BFS(Breadth First Search)广度优先搜索
DFS(Depth First Search)深度优先搜索
刚开始是在二叉树遍历中接触这两个算法,从中文名字上很好理解,广度优先就是优先搜索横向结点,深度优先就是优先纵向搜索根结点。用一个示意图Fg.1和Fg.2来表示

BFS输出:0 1 2 3 4 5
DFS输出:0 1 3 4 2 5
从二叉树过渡到图有两个变化,以有向图为例子:每个节点的子节点不一定是两个,节点间有方向性(如Fg.3)。

图的遍历要注意不要重复遍历节点。依然可以用BFS和DFS来做,用一个数组来储存每个节点是否被遍历(比如已经遍历置为true,没有遍历的为false)。BFS使用队列,DFS使用栈,详细的在这里不多说。
二、进阶:最短路径Dijkstra算法
如果我们在考虑最优路径的问题,图比Fg.3的有向图要复杂一些。
比如一个城市有很多镇,每个镇之间有多条路径可以到达,A镇到D镇没有直达路,要从A走到D,可能要经过B,也可能经过C,我们通常会选择最短的距离作为最优路径,这就要求我们在图中引入权值,且对于路径问题来说,权值一定为正数(如Fg.4)。

Dijkstra可以算出起始点到任意点的最短距离。它其实是BFS的加权版,引入了贪心算法的思想,从起始位置开始遍历子节点,每次都要选最短的路径走,直到遍历到目标位置。从局部最优到全局最优。
Dijkstra需要维护一个从起点到终点到路径及距离(权值)表格,可以用二维数组来存储。因为每个点都需要遍历到其他点的路径来更新表格,所以算法复杂度O(n2)。
三、启发式的搜索:最佳优先搜索 & A*算法
现实中找路也许更加复杂。假设我是一个路痴(其实我就是),我不知道A镇到D镇要走哪个方向,难道要一圈一圈扩大搜索范围来找吗?这时候如果使用Dijkstra算法,我需要从红色起点向周围扩展8个格子,再分别考虑这8个格子周围的8个格子,太慢了! 所以启发式搜索登场了。
如Fg.5所示,我站在红色的起点,但我不是茫然无措的,我还知道终点在哪,所谓启发,就是我的搜索是有方向性的。在此介绍最佳优先搜索(Greedy Best First Search)和A*算法。

那么我到底要往哪里走?最佳优先搜索和A*算法都引入了一个启发函数。
最佳优先算法: F = H 最佳优先算法:F=H 最佳优先算法:F=H
A ∗ 算法: F = G + H A*算法:F=G+H A∗算法:F=G+H
两种算法每次都是选取F最小的值。在这个等式中,G是到起点的距离,为确定值;H是到目标点的距离,为预测值。为了方便计算,我们将这些值扩大10倍。
G比较好理解,比如从起点向右走一格,G值为10(即1x10),向斜上方走一格,G值为14(即 2 \sqrt{2} 2x10)。
H即当前位置到终点的距离,有多种预测方法。在此我们展示Manhattan方法(使用曼哈顿距离),即忽略障碍物,考虑起点到终点的最短位移(只能往水平或竖直方向走),再扩大10倍得到H预测值。起点周围的方格的H值如Fg.6所示。

以A*算法为例,最后我们就可以计算出F值,如Fg.7所示,起点正右侧的格子F=G+H=10+50=60

它也是当前检索方块中F值最小的方块,就加入到路径中,如图Fg.8所示,然后再去探索当前粉色位置周围的F值(如果遇到障碍物,则忽略障碍物格子)。依次检索,直到终点。

可以看到最佳优先算法和A* 算法都是对Dijkstra算法的优化,引入启发函数使计算量大大减少,当H值为0的时候,最佳优先算法和A*就退化成了Dijkstra算法。
四、进一步优化:考虑动态环境的D*算法
A*算法用启发的方式探路,看上去已经很棒了。
还记得A*的公式吗:
F=G+H
G是当前节点到起点的确定距离,H是当前节点到终点的预测距离
不过现实总是更复杂一些,上面我们只是在图上放了几个固定的障碍物。那如果环境在变化,比如走着走着,障碍物移了动怎么办?
对于A*来说,即使障碍物只移动了很小的位移,但从当前位置到终点的路径也需要重新规划。如图Fg.9和Fg.10所示,障碍物(黑色方块)移动了1个单位位移,要重新计算一遍F值规划路径。粉色标c的部分其实是相同的路径,可否省略这部分计算呢?

D* 算法在A* 的基础上在1994年提出。针对动态环境的路径规划,增加了环境检测和更新影响路径这两个步骤。最重要的是,为了省略Fg.9和Fg.10中粉色标c的计算,D*决定从终点开始规划路径。
我们先大体看看A* 和D*的不同:
| A* | D* |
|---|---|
| 起点开始搜索 | 终点开始搜索 |
| 启发式搜索,环境变化需要重新规划路径 | 增量式搜索,环境变化可以利用先前已规划的信息 |
| F=G+H,每次取F最小值 | k=min { k , h_new},每次取k最小值 |
详细看下D* 的公式
k=min { k , h_new}
h_new表示当前位置到终点的确定距离(和A* 的G有点像)。
简单来理解D* 算法就是从终点向起点探索出一条最短路径。探索完后,调用行进函数出发,检测到环境变化(障碍物移动,或障碍物出现),就要调用修正函数来修正这条最短路径。
那问题来了,为什么类比A* 算法,直接k=h_new,而还要取k和h_new的最小值为更新值呢?我们再深入一点看下算法的实现:
D*维护一个OpenList队列来存储搜索节点,直到起始格子出队列就完成了一个路径搜索。
在算法的实现中,每个小格子会有三个状态,
- OPEN
- CLOSE
- NEW
OPEN表示被搜索的格子,即h_new值更新的格子;
CLOSE表示已加入规划路径的格子,即从OpenList中移除的格子;
NEW表示未曾被搜索的格子,h_new值初始化为正无穷。
试想,当环境变化,比如出现了障碍物,h_new值被更新为值正无穷。此时将这个变化的格子被加入到OpenList重新规划路径,因为OpenList是按照h_new排序后依次遍历更新周围节点的,所以这个突然出现的障碍物节点就会排到最后才遍历。但我们希望马上就能遍历这个障碍物节点但周围节点,所以需要k值,这样使效率提高不少。
每次环境变化要修正路径时,计算加入到OpenList的格子的k值,变小才加入到修正的路径中,否则停止搜索。
我们按照k值公式来举例子,如图Fg.11和Fg.12:
当前位置在粉红色格子,Fg.11->Fg.12 正右侧有障碍物突然出现,即B格子h_new的值被更新为正无穷,这时候计算k值,k值保持之前的k值不更新,这个格子不会被加入OpenList中。
再举个例子,当前位置在粉红色格子,Fg.12->Fg.11 正右侧障碍物突然移开,即B格子h_new的值被更新变小,这时候计算k值就比原来的k值小,即为h_new,此时这个变化的格子B会被加入到OpenList中重新规划路径。

照这样继续搜索,k>=h_new时停止更新,这样其实Fg.9和Fg.10中标有c的部分就不会被更新,减少了许多计算量。如此就完成了路径的修正。
小结:以上算法是需要先验知识的,即起点和终点并距离信息,这些信息可以通过路径规划前的扫描建图来获取。A* 多用于静态环境路径规划,D*多用于动态环境路径规划,是目前比较优秀的最短路径搜索算法。
相关文章:

【算法】最短路径算法思路小结
一、基础:二叉树的遍历->图的遍历 提到搜索算法,就不得不说两个最基础的思想: BFS(Breadth First Search)广度优先搜索 DFS(Depth First Search)深度优先搜索 刚开始是在二叉树遍历中接触这…...

zabbix7.0TLS-05-快速入门-触发器
文章目录 1 概述2 查看主机的触发器3 添加触发器3.1 触发器配置项介绍3.2 扩展文档3.2.1 关于配置项中每个键值返回值的说明3.2.2 触发器函数文档 4 验证触发器5 问题5.1 查了问题总列表5.2 查看问题详情5.3 更新处理问题5.4 查看已经处理的问题 6 问题恢复 1 概述 监控项用于…...

vue关于双向数据绑定的骚操作
组件传值大家都知道 直接上代码 computed: {optionModel: {get() {return this.selectedWidget.options;},set(newValue) {this.selectedWidget.options newValue;}}} 我们将optionModel传递给子组件 子组件可以直接修改props 来实现双向数据绑定 但是正常来时我们是不能修…...

基于Jeecgboot3.6.3的vue3版本的流程中仿钉钉流程的鼠标拖动功能支持
因为这个项目license问题无法开源,更多技术支持与服务请加入我的知识星球。 1、因为原先仿钉钉流程里不能进行鼠标拖动来查看流程,所以根据作者提供的信息进行修改,在hooks下增加下面文件useDraggableScroll.ts import { ref, onMounted, on…...
Docker Compse单机编排
一.Docker Compse 介绍 Docker Compose 是一个用于定义和运行多容器 Docker 应用程序的工具。通过 Compose,你可以使用 YAML 文件来配置应用程序的服务、网络和卷,然后使用单个命令创建和启动所有服务。这使得在开发、测试和部署过程中管理多容器应用程…...

“AI+Security”系列第2期(一):对抗!大模型自身安全的攻防博弈
近日,由安全极客、Wisemodel 社区和 InForSec 网络安全研究国际学术论坛联合主办的“AISecurity”系列第 2 期——对抗!大模型自身安全的攻防博弈线上活动如期举行。本次活动邀请了君同未来创始人兼 CEO 韩蒙、前阿里云高级安全专家郑瀚、ChaMd5 AI 组负…...

Python Static Typing: 提升代码可靠性与可读性的使用技巧
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storm…...

Datawhale多模态赛事(1)
赛事说明:https://tianchi.aliyun.com/competition/entrance/532251/introduction?spma2c22.12281925.0.0.2f307137p8qZmp 学习平台:https://linklearner.com/home 第一天 1.报名赛道学习赛事 https://tianchi.aliyun.com/competition/entrance/53225…...

云手机在海外社交媒体运营中的作用
随着社交媒体的全球普及,海外社交媒体运营成为众多企业与个人提升品牌影响力和扩大市场份额的重要策略。在这一进程中,海外云手机以其独特的功能,为海外社交媒体运营提供了强大的支持。 那么,海外云手机在海外社交媒体运营中究竟扮…...

Ubuntu怎么进入救援模式或单用户模式
进入救援模式(Rescue Mode)或单用户模式(Single User Mode)的方法取决于你所使用的Linux发行版。以下是通用的步骤,适用于大多数基于GRUB引导的系统,如Ubuntu、Debian、CentOS等: 重启你的系统。…...

学习鸿蒙-构建私有仓储
1.选择 鸿蒙提供ohpm-repo工具用于构建本地私有仓储 ohpm-repo下载 2.环境配置 安装node,ohpm-repo 支持 node.js 18.x 及以上版本 node最新版本下载 3.配置文件及运行 1.解压 ohpm-repo 私仓工具包 2.进入 ohpm-repo 解压目录的 conf 目录内,打开 c…...

经验是负债,学习是资产
经验是负债,学习是资产 经验是负债,学习是资产。这是李嘉诚先生的一句名言。他一语道出了学习在企业发展中的推动作用。 企业家经营的目的,无非就是将利润最大化。企业能够产生利润,靠的是提升自身业绩、降低运营成本,…...
电脑屏幕录制工具分享5款,附上详细电脑录屏教程(2024全新)
日月更迭,转眼间已经来到了2024年的立秋,在这个数字技术快速发展的时代,电脑录屏技术已经成为了一项不可或缺的技能,无论是用于工作汇报、在线教学、游戏直播还是个人娱乐。那么录屏软件哪个好用呢?接下来,…...

Docker资源隔离的实现策略以及适用场景
Docker通过多种技术实现资源隔离,确保不同容器之间相互独立并有效利用主机资源。 以下是Docker资源隔离的主要实现策略以及适用场景: 实现策略 1、命名空间(Namespaces) 进程命名空间(PID Namespace): 隔…...
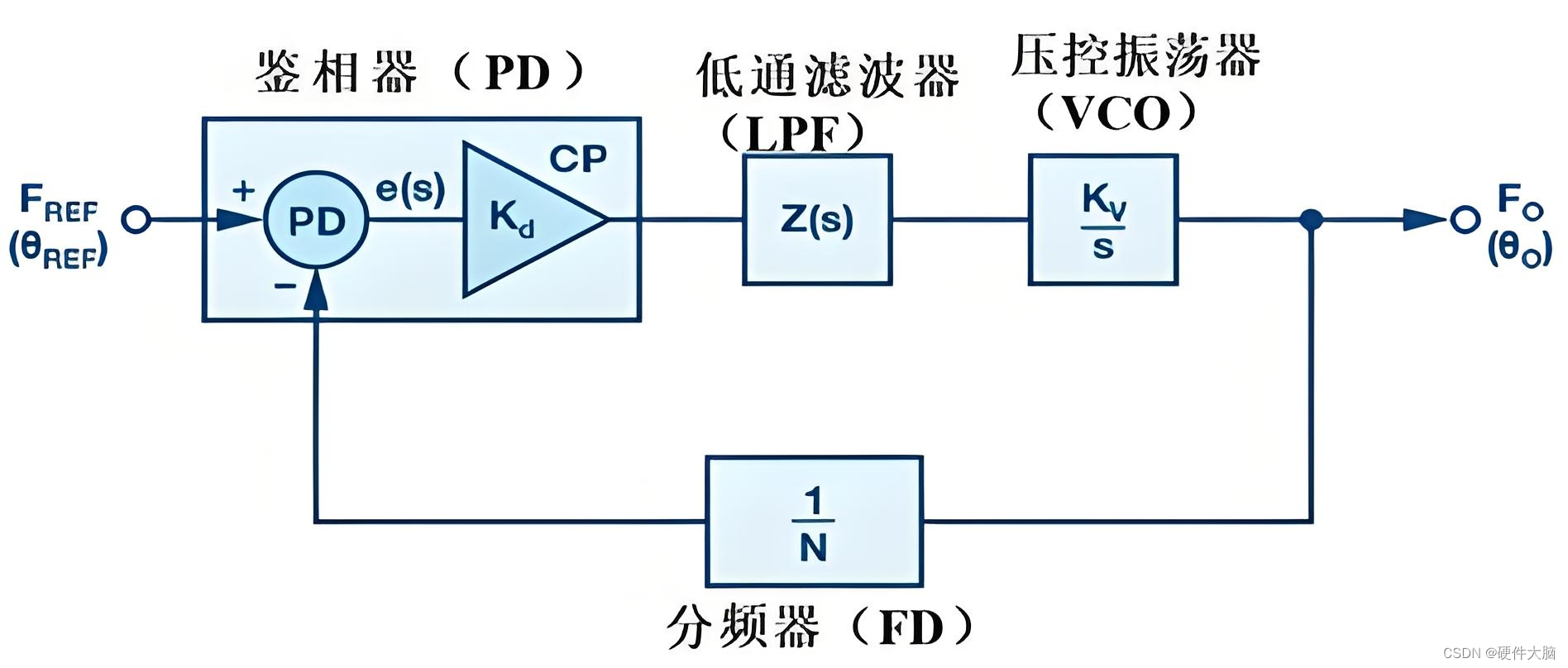
PLL基本原理、设计及应用
PLL基本原理 锁相环(Phase-Locked Loop, PLL)是一种基本的反馈控制系统,广泛应用于电子通信、信号处理、时钟同步等多个领域。PLL通过反馈机制锁定输入信号的频率和相位,从而实现输出信号与输入信号的同步。其基本工作原理可以概…...

Qt实现类似淘宝商品看板的界面,带有循环翻页以及点击某页跳转的功能
效果如下: #ifndef ModelDashboardGroup_h__ #define ModelDashboardGroup_h__#include <QGridLayout> #include <QLabel> #include <QPushButton> #include <QWidget>#include <QLabel> #include <QWidget> #include <QMou…...

2024下半年国际学术会议一览表
在科技与人文的交汇点,2024年的国际学术会议季即将拉开帷幕,一系列聚焦于计算机科学与人工智能、工程与技术、教育与社会科学的盛会,不仅展示了全球学术研究的最新成果,更促进了跨学科交流与合作,为未来的科技发展与社…...

serial靶场
项目地址 https://download.vulnhub.com/serial/serial.zip 实验过程 将下载好的靶机导入到VMware中,设置网络模式为NAT模式,然后开启靶机虚拟机 使用C段扫描,获取靶机IP地址 arp-scan -l 扫描一下端口 nmap -sV -p- 192.168.48.149 查看…...

如何在Vue3项目中引入并使用Echarts图表
在Vue 3项目中引入并使用ECharts图表,你可以通过npm或yarn来安装ECharts,然后在Vue组件中引入并使用它。以下是一个基本的步骤指南: 1. 安装ECharts 首先,你需要在你的Vue 3项目中安装ECharts。打开你的终端或命令提示符&#x…...

C# 子类、接口
栏目总目录 子类 继承的概念 继承机制:C#支持单继承,即一个类只能直接继承自一个基类。但基类本身可以继承自另一个类,从而实现继承链。继承关键字:使用冒号(:)表示继承关系,子类在声明时指定…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
