【langchain学习】使用缓存优化langchain中的LLM调用性能:内存、SQLite与Redis的对比
在处理语言模型(LLM)调用时,特别是在需要多次执行相同请求的情况下,缓存机制能够显著提升系统的性能。本文通过对比内存缓存(InMemoryCache)、SQLite缓存(SQLiteCache)和Redis缓存(RedisCache),探讨了如何在Langchain中使用这些缓存机制来优化LLM调用的性能。
代码实现与性能测试
我们在Python中实现了三种缓存机制,并测试了它们的性能。以下是完整的代码实现及其对应的执行结果。
内存缓存(InMemoryCache)
内存缓存是最简单的缓存机制,它将数据存储在内存中,具有极高的访问速度,但缺点是数据不会持久化,程序重启后缓存数据会丢失。
from langchain.globals import set_llm_cache
from config import llm
from langchain.cache import InMemoryCache
import time# 开始计时
start_time = time.time()# 设置内存缓存
set_llm_cache(InMemoryCache())# 第一次调用,由于缓存中没有内容,因此可能会较慢
llm.invoke("介绍一下2023年环法冠军温格高")# 结束计时
end_time = time.time()# 打印执行时间
print(f"Execution first time: {end_time - start_time相关文章:

【langchain学习】使用缓存优化langchain中的LLM调用性能:内存、SQLite与Redis的对比
在处理语言模型(LLM)调用时,特别是在需要多次执行相同请求的情况下,缓存机制能够显著提升系统的性能。本文通过对比内存缓存(InMemoryCache)、SQLite缓存(SQLiteCache)和Redis缓存(RedisCache),探讨了如何在Langchain中使用这些缓存机制来优化LLM调用的性能。 代码…...

spring boot 集成EasyExcel
EasyExcel 是一个基于 Java 的快速、简洁的 Excel 处理工具,它能够在不用考虑性能和内存等因素的情况下,快速完成 Excel 的读写功能。 首先,需要在 Spring Boot 项目中引入 EasyExcel 依赖。在 pom.xml 文件中添加以下依赖: <d…...

获取对象中第一个存在的值
在JavaScript中,要从一个对象中获取第一个存在的(非undefined、非null、非空数组等)值,你可以使用Object.values()方法结合Array.prototype.find()方法。以下是一个示例代码,演示如何实现这一点: const ob…...

Python学习笔记----集合与字典
1. 字符串、列表和元组的元素都是按下标顺序排列,可通过下 标直接访问,这样的数据类型统称为序列。 其中,字符串和元组中的元素不能修改,而列表中的元素可以修改。 集合 1. 与元组和列表类似,Set (集合&a…...

c# 排序、强转枚举
List<Tuple<double,int>> mm中doble从小到大排序 mm本身排序 在C#中,如果你有一个List<Tuple<double, int>>类型的集合mm,并且你想要根据Tuple中的double值(即第一个元素)从小到大进行排序,同…...

“华为杯”第十六届中国研究生数学建模竞赛-C题:视觉情报信息分析
目录 摘 要: 一、问题重述 二、模型假设 三、符号说明 四、问题一分析与求解 4.1 问题一分析 4.2 模型建立 4.2.1 位置变换模型建立 4.2.4 多平面转换模型建立 4.3 模型求解 4.3.1 问题一图 1 结果 4.3.2 问题一图 2 结果 4.3.3 问题一图 3 结果 4.3.4 问题一图 4 结果 4.4 模…...

html+css+js网页设计 找法网2个页面(带js)ui还原度百分之90
htmlcssjs网页设计 找法网2个页面(带js)ui还原度百分之90 网页作品代码简单,可使用任意HTML编辑软件(如:Dreamweaver、HBuilder、Vscode 、Sublime 、Webstorm、Text 、Notepad 等任意html编辑软件进行运行及修改编辑…...

018 | backtrader回测反转策略
什么是反转策略? 反转策略(Reversal Strategy)是一种试图捕捉市场价格趋势逆转的交易策略。与趋势跟随策略不同,反转策略的核心理念是“物极必反”,即价格在经过一段时间的单边趋势后,往往会出现逆转的机会…...

《图解HTTP》全篇目录
前言 目前,国内讲解 HTTP 协议的书实在太少了。在我的印象中,讲解网络协议的书仅有两本。一本是《HTTP 权威指南》,但其厚度令人望而生畏;另一本是《TCP/IP 详解,卷 1》,内容艰涩难懂,学习难度…...
+Qt的软件开发—环境配置)
基于VS2019(Release_x64)+Qt的软件开发—环境配置
前置博客: 基于C高级编程语言的软件开发随记——环境变量-CSDN博客 (一)一种避免设置大量环境变量的VS2019环境配置方法 Ⅰ 解决方案资源管理器->VC目录->在包含目录/库目录中添加对应的include/lib文件夹($(So…...

【书生大模型实战营(暑假场)闯关材料】入门岛:第1关 Linux 基础知识
【书生大模型实战营(暑假场)闯关材料】入门岛:第1关 Linux 基础知识 1. 使用VScode进行SSH远程连接服务器2. 端口映射及实例参考文献 这一博客主要介绍使用VScode进行服务器远程连接及端口映射。 1. 使用VScode进行SSH远程连接服务器 安装V…...

240810-Gradio通过HTML组件打开本地文件+防止网页跳转到about:blank
A. 最终效果 B. 可通过鼠标点击打开文件,但会跳转到about:blank import gradio as gr import subprocessdef open_pptx():pptx_path /Users/liuguokai/Downloads/240528-工业大模型1.pptxtry:subprocess.Popen([open, pptx_path])return "PPTX file opened s…...

go在linux上安装
1.首先要确定Linux架构 uname -m如果你的系统是 armv7l(32-bit ARM),你需要下载 armv6l 版的Go语言。 如果你的系统是 aarch64(64-bit ARM),你需要下载 arm64 版的Go语言。 如果你的系统是 x86_64…...
)
算法日记day 35(动归之分割等和子集|最后一块石头的重量2)
一、分割等和子集 题目: 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分…...
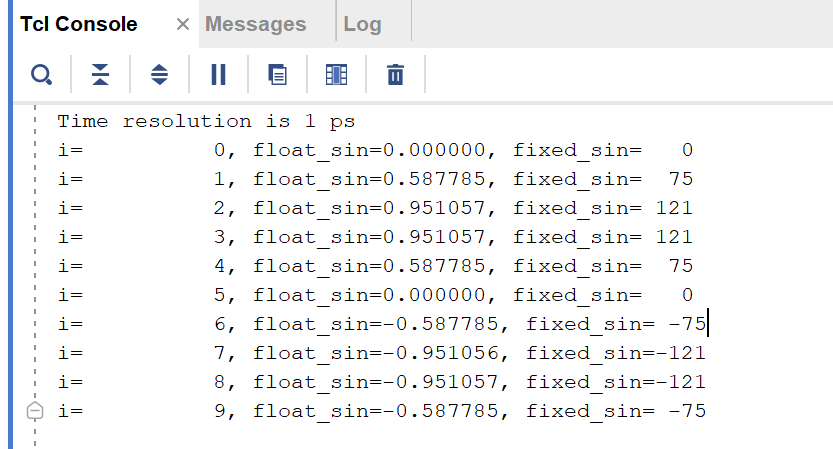
FPGA使用sv生成虚拟单音数据
FPGA使用sv生成虚拟单音数据 之前一直使用matlab生成虚拟的数据,导出到txt或是coe文件中,再导入到fpga中进行仿真测试。 复杂的数据这样操作自然是必要的,但是平日使用正弦数据进行测试的话,这样的操作不免复杂,今日…...

Linux shell编程:监控进程CPU使用率并使用 perf 抓取高CPU进程信息
0. 概要 本文将介绍一个用于监控一组进程CPU使用率的Shell脚本,,当检测到某进程的CPU使用率超出阈值时,使用 perf 工具抓取该进程的详细信息。 本shell脚本为了能在普通嵌入式系统上运行做了妥协和优化。 1. shell脚本流程的简要图示&#…...
)
Linux网络编程的套接字分析(其一,基本知识)
文章目录 套接字的类型流套接字数据报套接字原始套接字 套接字地址获取套接字地址 协议族和地址族 套接字的类型 Linux系统的套接字有三类:流套接字(SOCK_STREAM),数据报套接字(SOCK_DGRAM),原始套接字(SOCK_RAM)。 流套接字 用于面向连接…...

后端Web开发之Maven
1.java项目构建工具maven介绍 Maven是apache旗下的一个开源项目。Apache软件基金会,成立于1999年7月,是目前世界上最大的最受欢迎的开源(源代码开放)软件基金会也是一一个专门为支持开源项目而生的非盈利性组织。 apache开源项目…...

前端创新实践:用JavaScript打造网页扫码新体验
引言 简述扫码技术在现代网页应用中的普及和重要性。引入JavaScript实现网页扫码功能的创新性和实用性。 扫码技术概述 介绍扫码技术的原理和在不同平台(如微信、支付宝)的应用。讨论扫码技术对用户体验和业务流程的影响。 JavaScript实现网页扫码的…...

AWS CLI命令行
参考文档:在 macOS 上安裝,更新和卸載 AWS CLI 版本 1 - AWS Command Line Interface...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
 Module Federation:Webpack.config.js文件中每个属性的含义解释)
MFE(微前端) Module Federation:Webpack.config.js文件中每个属性的含义解释
以Module Federation 插件详为例,Webpack.config.js它可能的配置和含义如下: 前言 Module Federation 的Webpack.config.js核心配置包括: name filename(定义应用标识) remotes(引用远程模块࿰…...
