力扣 | 递增子序列 | 动态规划 | 最长递增子序列、最长递增子序列的个数、及其变式
文章目录
- 一、300. 最长递增子序列
- 二、673. 最长递增子序列的个数
- 三、变式
- 1、646. 最长数对链
- 2、1218. 最长定差子序列
- 3、1027. 最长等差数列
- 4、354. 俄罗斯套娃信封问题
- 5、1964. 找出到每个位置为止最长的有效障碍赛跑路线
最长递增子序列:原序-递增数值问题
最长定差子序列:原序-定差数值问题
最长数对链:非原序-递增区间问题
俄罗斯信封套娃:非原序-递增二维数值问题
一、300. 最长递增子序列
LeetCode:300. 最长递增子序列

一个很容易的解法,就是定义 d p [ i ] dp[i] dp[i]表示以第 i + 1 i+1 i+1个数字结尾的最长递增子序列长度,要求出这个长度,只需要往前遍历一次,看看前面有没有比它小的字符,这样就可以构成一个递增子序列。那么对于第 i + 1 i+1 i+1个字符而言,将它之前的所有数字遍历一遍可以求出最长递增子序列。
时间复杂度: O ( n 2 ) O(n^2) O(n2)

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);int ans = 1;for(int i = 1; i < nums.size(); ++ i){for(int j = i - 1; j >= 0; -- j){if(nums[i] > nums[j]){dp[i] = max(dp[i], dp[j] + 1);ans = max(ans, dp[i]);}}}return ans;}
};
不过我们知道要求出 d p [ i ] dp[i] dp[i]只需要找到前面比它小的数字即可。
我们可以动态维护一个最长递增序列,这样序列是这样的, l i s t [ i ] list[i] list[i]表示当前长度为 i + 1 i+1 i+1的递增子序列的末尾的最小数字。我们可以动态维护这样的数据结构。
- 当我们考虑 d p [ i ] dp[i] dp[i]时,我们可以通过 l i s t list list来快速求出 d p [ i ] dp[i] dp[i]的值(二分查找)。因为 l i s t list list是按递增子序列长度排列的,并且每一个长度都维护了一个最小值。
- 对于第 i + 1 i+1 i+1个数字,看它的递增长度 l e n len len 来与 l i s t [ l e n ] list[len] list[len]对比,维护 l i s t list list
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)

class Solution {
public:int lengthOfLIS(vector<int>& nums) {vector<int> lst;for(int i = 0; i < nums.size(); ++ i){int left = 0, right = (int) lst.size() - 1, mid;while(left <= right){//二分查找,查找小于nums[i]的最大值mid = (right - left) / 2 + left;if(lst[mid] >= nums[i]){right = mid - 1;}else left = mid + 1;}if(left == lst.size()) lst.emplace_back(nums[i]);if(lst[left] > nums[i]) lst[left] = nums[i];}return lst.size();}
};
二、673. 最长递增子序列的个数
LeetCode:673. 最长递增子序列的个数

这个题难度大很多!我们无法直接使用二分查找!因为我们维护的递增子序列是最小值!即使记录每个位置现在的个数也无法进行状态转移呀! 比如[1, 5 , 2 , 3],这里我们维护了[1, 5]作为长度为2的,现在我们加入2,现在长度为2变成了[1,2],但我们并不能说长度为2的有两个,这样加入3的时候,一共有两个长度为3的序列,[1,2,3]。原因就在于我们维护的递增子序列每次都是最小的,后面加入的更长并不一定前面更小的都能和他构成更长的
那我们先考虑直接暴力计算的方法吧!
我们不构造,直接二维循环。我们仍然使用 d p [ i ] dp[i] dp[i]表示第 i + 1 i+1 i+1个数字为尾部的最长递增子序列;我们使用 c n t [ i ] cnt[i] cnt[i]表示第 i + 1 i+1 i+1个数字为尾部的最长递增子序列的个数。
时间复杂度: O ( n 2 ) O(n^2) O(n2)
class Solution {
public:int findNumberOfLIS(vector<int>& nums) {vector<int> dp(nums.size(), 1);vector<int> cnt(nums.size(), 1);int mx = 1;int ans = 0;for(int i = 0; i < nums.size(); ++ i){for(int j = i - 1; j >= 0; -- j){if(nums[i] > nums[j]){if(dp[j] + 1 > dp[i]){dp[i] = dp[j] + 1;cnt[i] = cnt[j];}else{if(dp[j] + 1 == dp[i]){cnt[i] += cnt[j];}}}}if(dp[i] == mx){ans += cnt[i];}else{if(dp[i] > mx) mx = dp[i], ans = cnt[i];}}return ans;}
};
高阶思路:
对于300. 最长递增子序列的解法二,我们维护的一个标准的最小值。
如果我们能想到另外一点就太强了:
- 我们每次去替换 l i s t [ i ] list[i] list[i]实际上都是当前值 v a l val val比 l i s t [ i ] list[i] list[i]小,那么我们换一个想法,我们不去替换它,而是将 l i s t [ i ] list[i] list[i]扩展为一个数组,想替换最小值变为它加在这个数组的末尾,这样我们就能够保证,每次加入一个 v a l val val都能保证 l i s t [ i ] list[i] list[i]是单调非增的。而且跟我们不看数组的所有元素,只看最末尾的元素的话,实际上和300. 最长递增子序列一样,所以我们能够保证每次加入的是正确的位置。
- 这样做,我们就知道,我们考虑任何一个数 v a l val val时,它如果放在 l i s t [ i ] list[i] list[i]处,我们能够知道它能构成多少个长度为 i + 1 i+1 i+1的递增子序列,这个数量这跟 l i s t [ i − 1 ] list[i-1] list[i−1]有关,而且在 l i s t [ i − 1 ] list[i-1] list[i−1]的数都出现在 v a l val val之前,所以一定是可以进行状态转移的。

时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
class Solution {int binarySearch(int n, function<bool(int)> f) {int l = 0, r = n;while (l < r) {int mid = (l + r) / 2;if (f(mid)) {r = mid;} else {l = mid + 1;}}return l;}public:int findNumberOfLIS(vector<int> &nums) {vector<vector<int>> d, cnt;for (int v : nums) {int i = binarySearch(d.size(), [&](int i) { return d[i].back() >= v; });int c = 1;if (i > 0) {int k = binarySearch(d[i - 1].size(), [&](int k) { return d[i - 1][k] < v; });c = cnt[i - 1].back() - cnt[i - 1][k];}if (i == d.size()) {d.push_back({v});cnt.push_back({0, c});} else {d[i].push_back(v);cnt[i].push_back(cnt[i].back() + c);}}return cnt.back().back();}
};
以下问题我们只谈他们使用最长递增子序列的方式解决的方法。这里并不是说要你记住这个方法,而是理解他们为什么能这样用,扩展思维。
三、变式
1、646. 最长数对链
LeetCode:646. 最长数对链

这个问题最快速和方便是使用贪心算法,不过我们也可以线排序 然后像最长递增子序列一样,使用时间复杂度为 O ( n 2 ) O(n^2) O(n2)的动态规划。

贪心算法的证明:
对于任何一个数对链,首先对于任何一个维度,都是递增的;其次它构成的链也是递增的。我们来考察数对链中的其中任何一个数对,如果我们能找到满足要求的更小的数对(任何一维更小或者两维都能小),那么我可以将其替换。根据这个原因,我们可以将第二维排序,另一维按最小能满足条件的值来进行选择。
实际上将其映射到数轴上,可以发现我们最好选择两端都更小的且满足要求的,这样不会因为右端更大而导致有一些重叠不能选。这也是为什么我们每次都选择最小,而不选择一端大一端更小的。
2、1218. 最长定差子序列
1218. 最长定差子序列

这个题也一样直接像最长递增子序列一样,使用时间复杂度为 O ( n 2 ) O(n^2) O(n2)的动态规划。
当然为什么最长对数链需要排序,而他们不要? 因为他们求的是子序列顺序已经固定了。而最长对数链有两维,必须满足其中一维满足要求才能用这种动态规划方式。
但是不得不说这个题和最长递增子序列的区别是什么:
- 最长递增子序列的关系是增,而这里的关系是差
difference - 确定一个数
val,无法在最长递增子序列中确定它是哪一个,而这里可以确定它的前驱是val - difference。这样就可以引入哈希查找了!将 O ( n 2 ) O(n^2) O(n2)降为 O ( n ) O(n) O(n)
class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {unordered_map<int, int> mp;//以mp[i]结尾的最长递增子序列int mx = 1;for(int i = 0; i < arr.size(); ++ i){if(mp.count(arr[i] - difference) == 0){mp[arr[i]] = 1;}else{mp[arr[i]] = mp[arr[i] - difference] + 1;}mx = max(mx, mp[arr[i]]);}return mx;}
};
由于数字就那么大,使用数组进行存储比哈希表更快。但是我们需要注意一些问题:

- − 1 0 4 < = a r r [ i ] , d i f f e r e n c e < = 1 0 4 -10^4 <= arr[i], difference <= 10^4 −104<=arr[i],difference<=104,那么将其映射到正数里是 [ 0 , 2 × 1 0 4 ] [0,2×10^4] [0,2×104],千万别认为是 [ 0 , 1 0 8 ] [0,10^8] [0,108],两边同时加上 1 0 4 10^4 104,是两倍关系不是指数关系。
- 注意 a r r [ i ] − d i f f e r e n c e arr[i] - difference arr[i]−difference的取值范围是: [ − 2 × 1 0 4 , 2 × 1 0 4 ] [-2×10^4,2×10^4] [−2×104,2×104],所以得开的数组范围是 [ 0 , 4 × 1 0 4 ] [0,4×10^4] [0,4×104]
class Solution {
public:int longestSubsequence(vector<int>& arr, int difference) {int mx = 1;array<int, 40000 + 1> mp = {};for(int i = 0; i < arr.size(); ++ i){mp[arr[i] + 20000] = mp[arr[i] - difference + 20000] + 1;mx = max(mx, mp[arr[i] + 20000]);}return mx;}
};
3、1027. 最长等差数列
LeetCode:1027. 最长等差数列

这一题和之前的区别在于,等差的大小是不知道的,我们不能拿着一个数就确定我们需要的他的最长等差长度,因为这跟等差的大小有关,因此我们定义 d p [ i ] [ d ] dp[i][d] dp[i][d]表示以i结尾的等差为d的最长长度,我们只需要遍历d就能像最长定差子序列一样求解问题了。
不过我们需要注意两个问题:
- 定义
array时需要特别注意顺序,二维越界不一定会出错,容易混淆顺序 - 等差有正的有负的,因此等差的范围为 [ − 500 , 500 ] [-500,500] [−500,500],并且当一个数没有这样的等差值时,它自己当做等差数列,因此长度为1。
class Solution {
public:int longestArithSeqLength(vector<int>& nums) {array<array<int, 1001>, 501> dp = {};//注意定义的顺序,不如直接int dp[501][1001];int mx = 1;for(int i = 0; i < nums.size(); ++ i){for(int d = -500; d <= 500; ++ d){//等差的值if(nums[i] - d < 0 || nums[i] - d > 500) dp[nums[i]][d + 500] = 1;//当一个数没有这样的等差值时,它自己当做等差数列,因此长度为1else dp[nums[i]][d + 500] = dp[nums[i] - d][d + 500] + 1;mx = max(dp[nums[i]][d + 500], mx);}}return mx;}
};
4、354. 俄罗斯套娃信封问题
LeetCode:354. 俄罗斯套娃信封问题

乍一看这个题目好像跟LeetCode:646. 最长数对链一毛一样,最长对数链使用贪心能够解决,难道这道题也可以?答案是不可以,原因在于,信封一端更小,但另一端可能很大导致其他信封塞不下。
最长对数链之所以右端更小就更好的原因在于,它不会影响比它大的数对的选择,选择更大的可能这个更大的区间中间可以放多个,选择右端最小就不会有这样的问题 即右端优先。但信封任何一端都没有这样的优先权,两端是等价的。
这个题和数对链一样,它们不是子序列的问题,直接二重循环是不行的。我们必须知道本质,能变成子序列问题是因为,答案必然由“子序列”构成,而不能是其他的顺序。
那我们如果使用二重循环,那就需要保证问题的解是子序列,我们需要从答案中考虑:
- 答案保证了
w和h是单增的,那么我们在数组中尝试让w单增,那么选择时 答案是否就是这个子序列了呢?(很难想到吧) - 官解告诉我们,并不是,原因在于当
w存在相等的值时,我们仅仅看h的大小会有问题,实际上这些信封都不能套起来,因此我们需要保证w相同时,不会导致只考虑h出现问题。这里有两种方式:- ①保证
w相同时,h是降序,这样单考虑h构成的子序列不会出现把相同的宽度套在一起的情况。 - ②我们再来考虑一下
w,相同w的信封不被套起来。
- ①保证
信封套娃实际上可以转化为二维最长递增子序列的问题。
我们这样就发现了问题的本质:
(1)使用从前往后遍历的方式来查看当前值和之前值能构成的答案时,实际上就必须保证解是子序列。无论是维护答案还是二重循环。
(2)从答案中思考问题的结构,答案必须保证升序。因此将二维中的一维升序转换后,实际上答案必然就在转换后的子序列中(原因是答案必然是其中一维升序!这是非常神奇的点)
使用二重循环的方法:实际上将其中一维升序之后,就变成了最长递增子序列的问题。不作第二维处理就剔除一下升序那维相同的情况即可。
使用二分查找的方法:仅仅将其中一维升序不够,因为第二维放的位置是跟大小有关系的,无法做到通过另一维判断情况。那么为了保证一维相同时的情况不会被考虑,我们得对相同时的情况的另一维做处理。 我们要刨除相同一维的影响,直接使得另一维不可能构成答案,应该怎么做? 正确的做法是在保证一维升序的情况下,另一维降序,这样的话单独考虑这些宽度相同的信封时,他们不可能在子序列的情况下构成嵌套关系。 这样的话就一定不会出现导致相同宽度的信封被认为嵌套。
方法一: 二重循环
时间复杂度: O ( n 2 ) O(n^2) O(n2) 超时
不用二维降序,多加一个判断就好:
bool cmp(vector<int> & a, vector<int> & b){return a[0] < b[0];
}
class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end(), cmp);vector<int> dp(envelopes.size(), 1);int mx = 1;for(int i = 1; i < envelopes.size(); ++ i){for(int j = i - 1; j >= 0; -- j){if(envelopes[i][0] != envelopes[j][0] && envelopes[i][1] > envelopes[j][1]){dp[i] = max(dp[i], dp[j] + 1);mx = max(mx, dp[i]);}}}return mx;}
};
使用二维降序,直接就变成了最长递增子序列的问题:
bool cmp(vector<int> & a, vector<int> & b){if(a[0] == b[0]) return a[1] > b[1];return a[0] < b[0];
}
class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end(), cmp);vector<int> dp(envelopes.size(), 1);int mx = 1;for(int i = 1; i < envelopes.size(); ++ i){for(int j = i - 1; j >= 0; -- j){if(envelopes[i][1] > envelopes[j][1]){dp[i] = max(dp[i], dp[j] + 1);mx = max(mx, dp[i]);}}}return mx;}
};
方法二: 启发式排序 + 二分查找
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn)
bool cmp(vector<int> & a, vector<int> & b){if(a[0] == b[0]) return a[1] > b[1];return a[0] < b[0];
}
class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end(), cmp);int n = envelopes.size();vector<int> lst;for(int i = 0; i < n; ++ i){auto it = lower_bound(lst.begin(), lst.end(), envelopes[i][1]);//寻找大于等于的第一个位置,不要用upper因为等于也是不行的if(it == lst.end()){lst.emplace_back(envelopes[i][1]);}else{*it = min(*it, envelopes[i][1]);}}return (int) lst.size();}
};
方法三: 单维排序 + 二分查找
时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),虽然运行过慢,但实际上就是 O ( n l o g n ) O(nlogn) O(nlogn),慢的原因是判断的条件多了很多,空间大了一些。

这种方法官解没有提供(不是想拓展一下思路深度思考的,别看了,判断写的太长了,条件有点多)
还可以观察到一个有意思的事情,由于相同
w的信封是按顺序排列的,那我们一定会按顺序进行考虑,我们什么时候会出现错误的情况呢?
我们来考虑在求 最长递增子序列的个数时, 我们维护一个最长递增子序列 并维护每个位置有哪些数。对于相同宽度的信封 e 1 , e 2 , e 3 , e 4 e1,e2,e3,e4 e1,e2,e3,e4(从小到大排序,即 e 1 < e 2 < e 3 < e 4 e1<e2<e3<e4 e1<e2<e3<e4,对于当前维护的信封 m 1 , m 2 , m 3 , m 4 , m 5 m1,m2,m3,m4,m5 m1,m2,m3,m4,m5,如果将 e i ei ei替换 m 1 m1 m1 ~ m 4 m4 m4中的任何一个信封,不管 e i ei ei怎么替换最长长度都是对的,我们可以会替换成 e 1 , e 2 , e 3 , e 4 , m 5 e1,e2,e3,e4,m5 e1,e2,e3,e4,m5,这个时候我们随便举个例子 e 4 e4 e4的位置,代表的是以 e 4 e4 e4结尾的能构成长度为4的套娃!但实际上能行吗? 如果有这样的情况 m 2 < e 3 < e 4 < m 3 < m 4 m2 < e3< e4 <m3 < m4 m2<e3<e4<m3<m4,我们说当 e 3 e3 e3替换掉 m 3 m3 m3之后, e 4 e4 e4被认为放到 m 4 m4 m4的位置,这是对的嘛?显然是不对的, e 4 e4 e4根本无法构成更长的,所以出现错误。
如果我们同样来维护每个位置有哪些信封,这个时候你必须用 e 4 e4 e4和 e 3 e3 e3的位置里的所有信封进行比较,如果存在一个使得比 e 4 e4 e4更小(实际上只需要比一次),那么 e 4 e4 e4可以替换 m 4 m4 m4,如果不存在,那么 e 4 e4 e4需要被抛弃,因为它的作用不及 e 3 e3 e3。
但如果是这样的,我们考虑 m 1 < e 3 < m 2 < m 3 < e 4 < m 4 m1 < e3 < m2 < m3 < e4 < m4 m1<e3<m2<m3<e4<m4,这个时候又是什么情况? m 2 m2 m2一定被 e 3 e3 e3替换, e 4 e4 e4是否一定能替换 m 4 m4 m4?答案是一定的!因为即使没有 e 3 e3 e3的存在, e 4 e4 e4也一定能替换 m 4 m4 m4,有了并不影响,这样我们就可以写出一个新算法!并不需要第二维排序了,多加一个判断就行。(空间复杂度稍微高了一点点)
虽然我们知道有了个新方法,但是别忘了官解最好是第二维降序!这样就不会出现这样的问题了,因为这样第一维相同,第二维不可能构成答案了!
bool cmp(vector<int> & a, vector<int> & b){/*if(a[0] == b[0]) return a[1] < b[1];*/return a[0] < b[0];
}
class Solution {
public:int maxEnvelopes(vector<vector<int>>& envelopes) {sort(envelopes.begin(), envelopes.end(), cmp);vector<vector<vector<int>>> lst;for(int i = 0; i < envelopes.size(); ++ i){int left = 0, right = (int) lst.size() - 1, mid;while(left <= right){mid = (right - left) / 2 + left;if(lst[mid].back()[1] < envelopes[i][1]){left = mid + 1;}else{right = mid - 1;}}//right left,left是需要放的地方if(right == -1 || lst[right].back()[0] != envelopes[i][0]){//与前一个位置的最后一个信封宽度不相同:直接放就行if(left == lst.size()){lst.push_back({envelopes[i]});}else {if(lst[left].back()[0] == envelopes[i][0]){//考虑当前位置的最后一个是否和当前位置最后一个信封宽度相同,相同用小的替代if(lst[left].back()[1] > envelopes[i][1]){lst[left].back() = envelopes[i];}}else lst[left].emplace_back(envelopes[i]);}}else{//与前一个位置的最后一个信封宽度相同if(lst[right].size() >= 2){//前一个位置的信封至少要有两个才行 有一个肯定不能放if(lst[right][(int) lst[right].size() - 2][1] < envelopes[i][1])//有两个,看看是否能放if(left == lst.size()){lst.push_back({envelopes[i]});}else {if(lst[left].back()[0] == envelopes[i][0]){if(lst[left].back()[1] > envelopes[i][1]){lst[left].back() = envelopes[i];}}else lst[left].emplace_back(envelopes[i]);}}}}return lst.size();}
};
5、1964. 找出到每个位置为止最长的有效障碍赛跑路线
这个题实际上就是维护最长来使用二分查找的最长递增子序列的问题。唯一区别就是可以相同,相当于最长非减子序列。
class Solution {
public:vector<int> longestObstacleCourseAtEachPosition(vector<int>& obstacles) {vector<int> lst;vector<int> ans;int n = obstacles.size();for(int i = 0; i < n; ++ i){auto it = upper_bound(lst.begin(), lst.end(), obstacles[i]);if(it == lst.end()){lst.emplace_back(obstacles[i]);ans.emplace_back(lst.size());}else{*it = min(*it, obstacles[i]);ans.emplace_back(it - lst.begin() + 1);}}return ans;}
};
相关文章:

力扣 | 递增子序列 | 动态规划 | 最长递增子序列、最长递增子序列的个数、及其变式
文章目录 一、300. 最长递增子序列二、673. 最长递增子序列的个数三、变式1、646. 最长数对链2、1218. 最长定差子序列3、1027. 最长等差数列4、354. 俄罗斯套娃信封问题5、1964. 找出到每个位置为止最长的有效障碍赛跑路线 最长递增子序列:原序-递增数值问题 最长定…...

008 | 基于RNN和LSTM的贵州茅台股票开盘价预测
基于RNN和LSTM的贵州茅台股票开盘价预测 项目简介: 本项目旨在通过使用Tushare下载贵州茅台的股票数据,并基于这些历史数据,使用TensorFlow 2.0实现循环神经网络(RNN)和长短期记忆网络(LSTM)来…...

尚硅谷谷粒商城项目笔记——六、使用navciat连接docker中的mysql容器【电脑CPU:AMD】
六、使用navciat连接docker中的mysql容器 注意: 因为电脑是AMD芯片,自己知识储备不够,无法保证和课程中用到的环境一样,所以环境都是自己根据适应硬件软件环境重新配置的,这里的虚拟机使用的是VMware。 1navicat免费…...
)
【git】本地更改了,但又想直接从远端拉取覆盖本地(放弃本地更改前行下载)
拉取时错误信息 error: cannot pull with rebase: You have unstaged changes. error: Please commit or stash them.个错误信息表明你在尝试使用git pull --rebase命令时,你的工作目录中存在未提交的更改(即未暂存(unstaged)的更…...
基于JSP的书店仓库管理系统
你好呀,我是计算机学姐码农小野!如果有相关需求,可以私信联系我。 开发语言:JSP 数据库:MySQL 技术:JSPJava 工具:ECLIPSE、Tomcat 系统展示 首页 管理员功能模块 用户功能模块 员工功能模…...

pytorch框架保存和加载模型
在 PyTorch 中,有几种常见的方法来保存和加载模型,具体方法取决于你想保存什么内容(例如,只保存模型的权重,还是保存整个模型)。下面我将介绍几种常见的保存和加载模型的方法。 1、保存和加载模型的 state…...

开发输出防护栏以检测GPT-4o幻觉
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
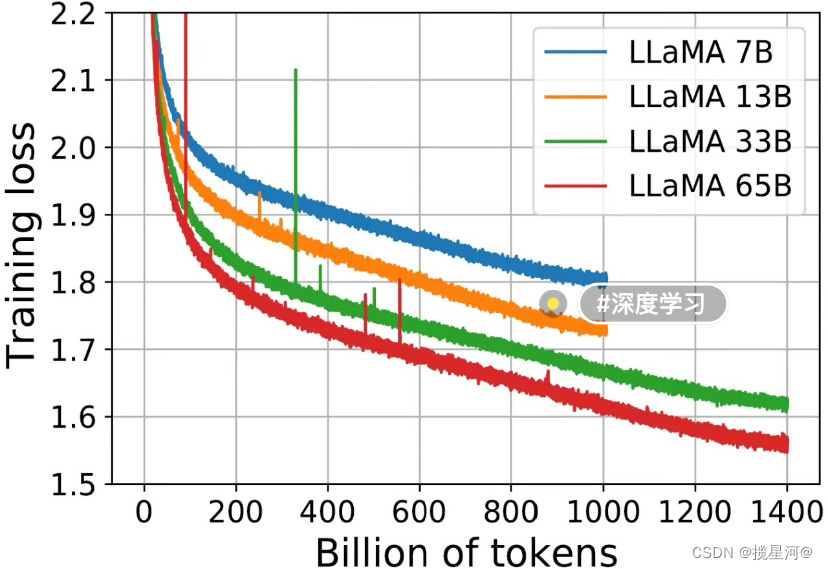
代码复现,代码改进,算法复现,模型复现
目前空闲可接硕士,博士,代码复现,改进代码,文献复现,算法复现,模型复现,文章复现,科研复现,可定制创新点,对比,模块,创新思路…...
基于STM32开发的智能机器人系统
目录 引言环境准备工作 硬件准备软件安装与配置系统设计 系统架构硬件连接代码实现 初始化代码控制代码应用场景 自动导航机器人家用服务机器人常见问题及解决方案 常见问题解决方案结论 1. 引言 智能机器人通过整合传感器、控制器和执行机构,能够自主完成环境感…...

【数据结构题目】循环队列,以及队列实现栈的模拟
前言: 🌟🌟Hello家人们,这期讲解数据结构队列的基础知识,希望你能帮到屏幕前的你。 📚️上期博客在这里:http://t.csdnimg.cn/oOkvk 📚️感兴趣的小伙伴看一看小编主页:G…...

大数据CloudSim应用实践:基于CloudSimExamle6.java修改(超详细教程)
文章目录 大数据CloudSim应用实践:基于CloudSimExamle6.java修改(超详细教程)1 准备1.1 操作系统1.2 软件 2 安装JDK2.1 安装JDK 3 配置Eclipse集成开发环境3.1 启动Eclipse3.2 配置Java运行时环境JRE 4 创建Java项目4.1 创建项目4.2 导入jar…...

完美解决浏览器的输入框自动填入时,黄色背景问题,以及图标被遮住问题(最新)
用图说话↓↓↓ 首先用代码解决黄色背景问题,box-shadow颜色设置透明即可,延时渲染时间可修改为更久 :deep(input:-webkit-autofill) {box-shadow: 0 0 0 1000px transparent !important;/* 浏览器记住密码的底色的颜色 */-webkit-text-fill-color: #f…...

C 语言中的头文件
1、C 语言中 include <> 与include “” 的区别? #include < > 引用的是编译器的类库路径里面的头文件。 #include " " 引用的是你程序目录的相对路径中的头文件,如果在程序目录没有找到引用的头文件则到编译器的类库路径的目录下找该头文…...

数据结构复杂度
文章目录 一. 数据结构前言1.1 数据结构1.2 算法 二. 算法效率2.1 时间复杂度2.1.1 T(N)函数式2.1.2 大O的渐进表示法 2.2 空间复杂度2.3 常见复杂度比较 2.3 复杂度算法题1.2. 一. 数据结构前言 1.1 数据结构 什么是数据结构呢?打开一个人的主页,有很…...

MySQL基础篇
一、MySQL概述 MySQL是一个数据库管理系统,由瑞典MySQL AB公司开发,属于Oracle推出的产品。MySQL是最流行的关系型数据库管理系统之一,在WEB应用方面,MySQL是最好的RDBMS(关系数据库管理系统) ,…...

详解C++中的四种强制转换reinterpret_cast / const_cast / static_cast / dynamic_cast
目录 1.reinterpret_cast 2.const_cast 3.static_cast 4.dynamic_cast 例子 C中存在四种强制转换:reinterpret_cast / const_cast / static_cast / dynamic_cast 1.reinterpret_cast 格式 : reinterpret_cast<type_id> (expression) 用于类型…...

Word中加载Mathtype后粘贴复制快捷键(Ctrl+C/V)不能使用
操作环境 windows 11操作系统 word版本2021 mathtype版本7.4 这个问题只出现在word中,在excel和ppt中都不存在这个问题,而且之前在另一台电脑中使用word2016版本并没有这种问题的,然后网上搜了一下有不少人有这种问题,word直接取…...

Linux硬件-bios
作者介绍:简历上没有一个精通的运维工程师。希望大家多多关注作者,下面的思维导图也是预计更新的内容和当前进度(不定时更新)。 在Linux的服务器领域,我们能接触的到硬件其实挺多的,但是在这些硬件我们根据我们的需要去使用的时候…...

VisionPro二次开发学习笔记12-使用CogToolGroup控件进行图像检测
本示例演示了如何通过图像数据库使用 CogImageFileTool,并将其放入 CogToolGroup 中,对于数据库中的每个图像运行一次检测. 当用户按下 RunTest 按钮时,程序执行以下操作: 如果工具组中没有 CogImageFileTools,它将显…...

mfc140u.dll丢失的科学修复手段,简单又方便的mfc140u.dll修复
遇到 "缺失 mfc140u.dll 文件" 的提示时可能会让你疑惑,但不用担心。这个文件是 Microsoft Visual C 2015 的重要组成部分,对运行特定程序非常关键。幸运的是,解决这一问题并不难。本文将简单指导你如何恢复或修复丢失的 mfc140u.d…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
