【数据结构】六、图：2.邻接矩阵、邻接表（有向图、无向图、带权图）

二、存储结构

❗1.邻接矩阵

图的邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。

用1表示有边，0表示没有边。

结点数为n的图G，邻接矩阵A是一个n*n的方阵，将G顶点编号为$v_1,v_2,...,v_n$：
$$A[i][j]=\{\begin{array}{ll}1,& 若边集E(G)中有(v_i,v_j)or<v_i,v_j>\\ 0,& 若边集E(G)中没有(v_i,v_j)or<v_i,v_j>\end{array}$$
存储结构定义：

#define MaxVertexNum 100	//顶点数目的最大值
typedef char VertexType;  //顶点的数据类型
typedef int EdgeType;     //带权图中边上权值的数据类型typedef struct{VertexType Vex[MaxVertexNum] ;	//顶点表:存放结构or信息EdgeType Edge[MaxVertexNum][MaxVertexNum];	//邻接矩阵，边表int vexnum, edgenum;		//图的当前顶点数和边数/弧数
}MGraph;

1.1无向图

1. 无向图的邻接矩阵一定是一个对称矩阵（即从矩阵的左上角到右下角的主对角线为轴，右上角的元与左下角相对应的元全都是相等的）。

   因此，在存储邻接矩阵时只需存储上(或下)三角矩阵的元素。

2. 对于无向图，第i个结点的度 = 邻接矩阵的**第i行(或第i列)**非零元素(或非∞元素)的个数。

   顶点A的度就是0+1+1+1+0+0=3。

❗邻接矩阵-无向图代码-C

/* 图邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。无向图C实现
*/#include <stdio.h>
#include <string.h>
#define MaxVertexNum  100 //顶点数目最大值
typedef char VertexType;  //顶点的数据类型
typedef int EdgeType;     //带权图中边上权值的数据类型#define numVertexes 6   // 顶点个数，用于visited数组
#define numEdges 7      // 边个数typedef struct
{VertexType Vex[MaxVertexNum];   //顶点表EdgeType Edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表int vexnum, edgenum;    //图的顶点数和弧数
}MGraph;void create_Graph(MGraph *G);
void create_Graph_ByArray(MGraph *G, int edges[][3]);
void print_Matrix(MGraph G);
void DFS(MGraph G,int v);
void DFSTraverse(MGraph G);
void BFS(MGraph G, int v);
void BFSTraverse(MGraph G);int main()
{MGraph G;// 创建无向图方法1//create_Graph(&G);// 创建无向图方法2//这里可以使用int，因为edge的EdgeType是intint edges[numEdges][3] = {  // 边的起点序号，终点序号，权值{1,2,5},{1,3,1},{1,4,6},{2,5,3},{2,6,4},{3,5,3},{4,6,2}};create_Graph_ByArray(&G,edges);print_Matrix(G);printf("\nDFS:");DFS(G,0);printf("\nBFS:");BFS(G,0);printf("\nBFS直接遍历(非连通图):");BFSTraverse(G);return 0;
}// 创建无向图
void create_Graph(MGraph *G){int i, j;int start, end;  //边的起点序号、终点序号int w;   //边上的权值// 所创建无向图的顶点数和边数(用空格隔开)。这里也可以输入G->vexnum = numVertexes;G->edgenum = numEdges;printf("\n");//图的初始化initfor (i=0; i<G->vexnum; i++){for (j=0; j<G->vexnum; j++){if (i == j)G->Edge[i][j] = 0;      //结点自身elseG->Edge[i][j] = 32767;   //初始都为表示∞}}//顶点信息存入顶点表for (i=0; i<G->vexnum; i++){// printf("请输入第%d个顶点的信息(int):",i+1);// scanf("%d", &G->Vex[i]);//这里不输入了，暂时默认0开始G->Vex[i] = i+1;}printf("\n");//输入无向图边的信息for (i=0; i<G->edgenum; i++){printf("请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：");scanf("%d%d%d", &start, &end, &w);G->Edge[start-1][end-1] = w;G->Edge[end-1][start-1] = w;   //无向图具有对称性}
}// 创建无向图
void create_Graph_ByArray(MGraph *G, int edges[][3]){int i, j;int start, end;  //边的起点序号、终点序号int w;   //边上的权值// 所创建无向图的顶点数和边数(用空格隔开)。这里也可以输入G->vexnum = numVertexes;G->edgenum = numEdges;printf("\n");//图的初始化initfor (i=0; i<G->vexnum; i++){for (j=0; j<G->vexnum; j++){if (i == j)G->Edge[i][j] = 0;      //结点自身elseG->Edge[i][j] = 32767;   //初始都为表示∞}}//顶点信息存入顶点表for (i=0; i<G->vexnum; i++){// printf("请输入第%d个顶点的信息(int):",i+1);// scanf("%d", &G->Vex[i]);//这里不输入了，暂时默认0开始G->Vex[i] = i+1;}printf("\n");// 输入无向图边的信息for (i=0; i<G->edgenum; i++){start = edges[i][0];end = edges[i][1];w = edges[i][2];G->Edge[start-1][end-1] = w;G->Edge[end-1][start-1] = w;   //无向图具有对称性}
}// 输出图
void print_Matrix(MGraph G){int i, j;printf("\n图的顶点为:");for (i=0; i<G.vexnum; i++)printf("%d ", G.Vex[i]);printf("\n输出邻接矩阵:\n");// 横坐标printf(" "); //表示行坐标，前面空格留给纵坐标for (i=0; i<G.vexnum; i++)printf("%5d", G.Vex[i]);printf("\n");for (i=0; i<G.vexnum; i++){// 纵坐标printf("\n%d", G.Vex[i]);// 输出邻接矩阵for (j=0; j<G.vexnum; j++){if (G.Edge[i][j] == 32767)printf("%7s", "∞");elseprintf("%5d", G.Edge[i][j]);}printf("\n");}	
}// ------------------------- DFS 深度优先遍历------------------------
int visited[numVertexes]={0};
// 注意：是从0下标开始
void DFS(MGraph G, int x){// 访问顶点xprintf("%d",G.Vex[x]);visited[x]=1;   //设已访问标记// 遍历x的邻接顶点for(int v=0; v<G.vexnum; v++){//i为x的尚未访问的邻接顶点if(!visited[v] && G.Edge[x][v] != 32767){DFS(G, v);}}
}
//对非连通图进行深度优先遍历
void DFSTraverse(MGraph G){//把所有结点全部标记为false，表示没有访问过for(int v=0; v<G.vexnum; v++){visited[v] = 0;}for(int v=0; v<G.vexnum; v++){	//从v=0开始遍历if(!visited[v]){DFS(G, v);}}
}/// @brief /辅助队列
typedef struct{int data[numVertexes];int f,r;
}Que;
void InitQueue(Que &Q){Q.f=Q.r=0;
}
void In(Que &Q,int e){if ((Q.r+1)%numVertexes==Q.f) return; Q.data[Q.r]=e;Q.r=(Q.r+1)%numVertexes;
}
void Out(Que &Q,int &e){if(Q.f==Q.r) return;e=Q.data[Q.f];Q.f=(Q.f+1)%numVertexes;
}// ------------------------- BFS 广度优先遍历------------------------
// 对连通图进行广度优先遍历
void BFS(MGraph G, int v){Que Q;InitQueue(Q);	//初始化一辅助用的队列//把所有结点全部标记为false，表示没有访问过for(int i=0; i<G.vexnum; i++){visited[i] = 0;}printf("%d",G.Vex[v]);visited[v]=1;In(Q,v);while(Q.f!=Q.r){Out(Q,v);//把出队结点的相邻的所有结点入队for(int w=0; w<G.vexnum; w++){if(!visited[w] && G.Edge[v][w] != 32767){printf("%d",G.Vex[w]);visited[w]=1;In(Q,w);}}}}// 对非连通图的广度遍历
void BFSTraverse(MGraph G){Que Q;InitQueue(Q);	//初始化一辅助用的队列int v;//把所有结点全部标记为false，表示没有访问过for(v=0; v<G.vexnum; v++){visited[v] = 0;}for(v=0; v<G.vexnum; v++){		//这里是从0开始//若是未访问过就处理if(!visited[v]){printf("%d",G.Vex[v]);visited[v]=1;In(Q,v);while(Q.f!=Q.r){Out(Q,v);//把出队结点的相邻的所有结点入队for(int w=0; w<G.vexnum; w++){if(!visited[w] && G.Edge[v][w] != 32767){printf("%d",G.Vex[w]);visited[w]=1;In(Q,w);}}}}}}

请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：1 2 5
请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：1 3 1
请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：1 4 6
请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：2 5 3
请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：2 6 4
请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：3 5 3
请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：4 6 2

图的顶点为:1 2 3 4 5 6
输出邻接矩阵:
1 2 3 4 5 6

1 0 5 1 6 ∞ ∞

2 5 0 ∞ ∞ 3 4

3 1 ∞ 0 ∞ 3 ∞

4 6 ∞ ∞ 0 ∞ 2

5 ∞ 3 3 ∞ 0 ∞

6 ∞ 4 ∞ 2 ∞ 0

DFS:125364
BFS:123456
BFS直接遍历(非连通图):123456

1.2有向图

主对角线上数值依然为0。但因为是有向图，所以此矩阵并不对称。

【注意】行是出度

有向图讲究入度与出度，
第i个结点的入度 = 邻接矩阵的第i列的非零元素的个数。（竖着）
第i个结点的出度 = 邻接矩阵的第i行的非零元素的个数。（横着）
第i个结点的度 = 第i行、第i列的非零元素个数之和。

❗邻接矩阵-有向图代码-C

与无向图的区别，仅有在构造的时候：

G->Edge[start-1][end-1] = w;
//有向图不具有对称性

code:

/* 图邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。有向图C实现
*/#include <stdio.h>
#include <string.h>
#define MaxVertexNum  100 //顶点数目最大值
typedef char VertexType;  //顶点的数据类型
typedef int EdgeType;     //带权图中边上权值的数据类型#define numVertexes 6   // 顶点个数，用于visited数组
#define numEdges 7      // 边个数typedef struct
{VertexType Vex[MaxVertexNum];   //顶点表EdgeType Edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表int vexnum, edgenum;    //图的顶点数和弧数
}MGraph;void create_Graph(MGraph *G);
void create_Graph_ByArray(MGraph *G, int edges[][3]);
void print_Matrix(MGraph G);
void DFS(MGraph G,int v);
void DFSTraverse(MGraph G);
void BFS(MGraph G, int v);
void BFSTraverse(MGraph G);int main()
{MGraph G;// 创建有向图方法1//create_Graph(&G);// 创建有向图方法2//这里可以使用int，因为edge的EdgeType是intint edges[numEdges][3] = {  // 边的起点序号，终点序号，权值{1,2,5},{3,1,1},{4,1,6},{5,2,3},{5,3,3},{6,2,4},{6,4,2}};create_Graph_ByArray(&G,edges);print_Matrix(G);printf("\nDFS:");DFS(G,0);printf("\nDFS直接遍历(非连通图):");DFSTraverse(G);printf("\nBFS:");BFS(G,0);printf("\nBFS直接遍历(非连通图):");BFSTraverse(G);return 0;
}// 创建有向图
void create_Graph(MGraph *G){int i, j;int start, end;  //边的起点序号、终点序号int w;   //边上的权值// 所创建有向图的顶点数和边数(用空格隔开)。这里也可以输入G->vexnum = numVertexes;G->edgenum = numEdges;printf("\n");//图的初始化initfor (i=0; i<G->vexnum; i++){for (j=0; j<G->vexnum; j++){if (i == j)G->Edge[i][j] = 0;      //结点自身elseG->Edge[i][j] = 32767;   //初始都为表示∞}}//顶点信息存入顶点表for (i=0; i<G->vexnum; i++){// printf("请输入第%d个顶点的信息(int):",i+1);// scanf("%d", &G->Vex[i]);//这里不输入了，暂时默认0开始G->Vex[i] = i+1;}printf("\n");//输入有向图边的信息for (i=0; i<G->edgenum; i++){printf("请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：");scanf("%d%d%d", &start, &end, &w);G->Edge[start-1][end-1] = w;//有向图不具有对称性}
}// 创建有向图
void create_Graph_ByArray(MGraph *G, int edges[][3]){int i, j;int start, end;  //边的起点序号、终点序号int w;   //边上的权值// 所创建有向图的顶点数和边数(用空格隔开)。这里也可以输入G->vexnum = numVertexes;G->edgenum = numEdges;printf("\n");//图的初始化initfor (i=0; i<G->vexnum; i++){for (j=0; j<G->vexnum; j++){if (i == j)G->Edge[i][j] = 0;      //结点自身elseG->Edge[i][j] = 32767;   //初始都为表示∞}}//顶点信息存入顶点表for (i=0; i<G->vexnum; i++){// printf("请输入第%d个顶点的信息(int):",i+1);// scanf("%d", &G->Vex[i]);//这里不输入了，暂时默认0开始G->Vex[i] = i+1;}printf("\n");// 输入有向图边的信息for (i=0; i<G->edgenum; i++){start = edges[i][0];end = edges[i][1];w = edges[i][2];G->Edge[start-1][end-1] = w;//有向图不具有对称性}
}// 输出图
void print_Matrix(MGraph G){int i, j;printf("\n图的顶点为:");for (i=0; i<G.vexnum; i++)printf("%d ", G.Vex[i]);printf("\n输出邻接矩阵:\n");// 横坐标printf(" "); //表示行坐标，前面空格留给纵坐标for (i=0; i<G.vexnum; i++)printf("%5d", G.Vex[i]);printf("\n");for (i=0; i<G.vexnum; i++){// 纵坐标printf("\n%d", G.Vex[i]);// 输出邻接矩阵for (j=0; j<G.vexnum; j++){if (G.Edge[i][j] == 32767)printf("%7s", "∞");elseprintf("%5d", G.Edge[i][j]);}printf("\n");}	
}// ------------------------- DFS 深度优先遍历------------------------
int visited[numVertexes]={0};
// 注意：是从0下标开始
void DFS(MGraph G, int x){// 访问顶点xprintf("%d",G.Vex[x]);visited[x]=1;   //设已访问标记// 遍历x的邻接顶点for(int v=0; v<G.vexnum; v++){//i为x的尚未访问的邻接顶点if(!visited[v] && G.Edge[x][v] != 32767){DFS(G, v);}}
}
//对非连通图进行深度优先遍历
void DFSTraverse(MGraph G){//把所有结点全部标记为false，表示没有访问过for(int v=0; v<G.vexnum; v++){visited[v] = 0;}for(int v=0; v<G.vexnum; v++){	//从v=0开始遍历if(!visited[v]){DFS(G, v);}}
}/// @brief /辅助队列
typedef struct{int data[numVertexes];int f,r;
}Que;
void InitQueue(Que &Q){Q.f=Q.r=0;
}
void In(Que &Q,int e){if ((Q.r+1)%numVertexes==Q.f) return; Q.data[Q.r]=e;Q.r=(Q.r+1)%numVertexes;
}
void Out(Que &Q,int &e){if(Q.f==Q.r) return;e=Q.data[Q.f];Q.f=(Q.f+1)%numVertexes;
}// ------------------------- BFS 广度优先遍历------------------------
// 对连通图进行广度优先遍历
void BFS(MGraph G, int v){Que Q;InitQueue(Q);	//初始化一辅助用的队列//把所有结点全部标记为false，表示没有访问过for(int i=0; i<G.vexnum; i++){visited[i] = 0;}printf("%d",G.Vex[v]);visited[v]=1;In(Q,v);while(Q.f!=Q.r){Out(Q,v);//把出队结点的相邻的所有结点入队for(int w=0; w<G.vexnum; w++){if(!visited[w] && G.Edge[v][w] != 32767){printf("%d",G.Vex[w]);visited[w]=1;In(Q,w);}}}}// 对非连通图的广度遍历
void BFSTraverse(MGraph G){Que Q;InitQueue(Q);	//初始化一辅助用的队列int v;//把所有结点全部标记为false，表示没有访问过for(v=0; v<G.vexnum; v++){visited[v] = 0;}for(v=0; v<G.vexnum; v++){		//这里是从0开始//若是未访问过就处理if(!visited[v]){printf("%d",G.Vex[v]);visited[v]=1;In(Q,v);while(Q.f!=Q.r){Out(Q,v);//把出队结点的相邻的所有结点入队for(int w=0; w<G.vexnum; w++){if(!visited[w] && G.Edge[v][w] != 32767){printf("%d",G.Vex[w]);visited[w]=1;In(Q,w);}}}}}}

1.3带权图

对于带权图而言,若顶点vi和vj之间有边相连，则邻接矩阵中对应项存放着该边对应的权值。

没有边，那么距离就是无穷。

自己指向自己，那么边就是0。

1.4性能分析

一个一维数组，一个二维数组，存储空间是O(n) + O(n²) = O(n²) ，即O(IVI²)。

邻接矩阵法求顶点的度/出度/入度的时间复杂度为O(IVI)。

适合用于稠密图。

1.5相乘

设图 G 的邻接矩阵为 A（矩阵元素为0/1），则Aⁿ的元素 Aⁿ[i][j] 等于由顶点 i 到顶点 j 的长度为 n 的路径的数目。

比如：

A²[1][4]：就是从A->B，然后B->D，这样两次（路径长度为2）的。

A²[1][4] = 1，意思就是满足长度为2的路径，只有一条。

A³同理，表示路径长度为 3 的路径数目。

❗2.邻接表

顺序+链式存储

• 不足

当一个图为稀疏图时（边数相对顶点较少），使用邻接矩阵法显然要浪费大量的存储空间，如下图所示：

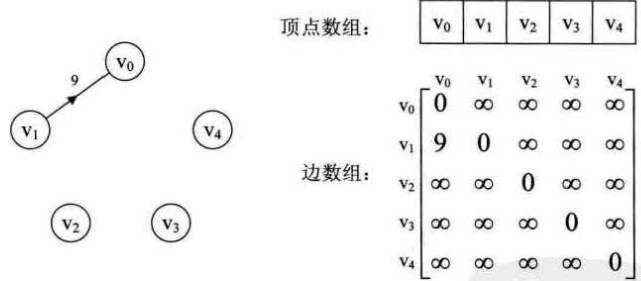
• 邻接表(Adjacency List)

而图的邻接表法结合了顺序存储 + 链式存储方法，减少了这种不必要的浪费。

所谓邻接表，是指对图G中的每个顶点 vi 建立一个单链表，第 i 个单链表中的结点表示依附于顶点 vi 的边，这个单链表就称为顶点 vi 的边表。

​ 那么，一个结点的出度就是单链表内的结点个数。

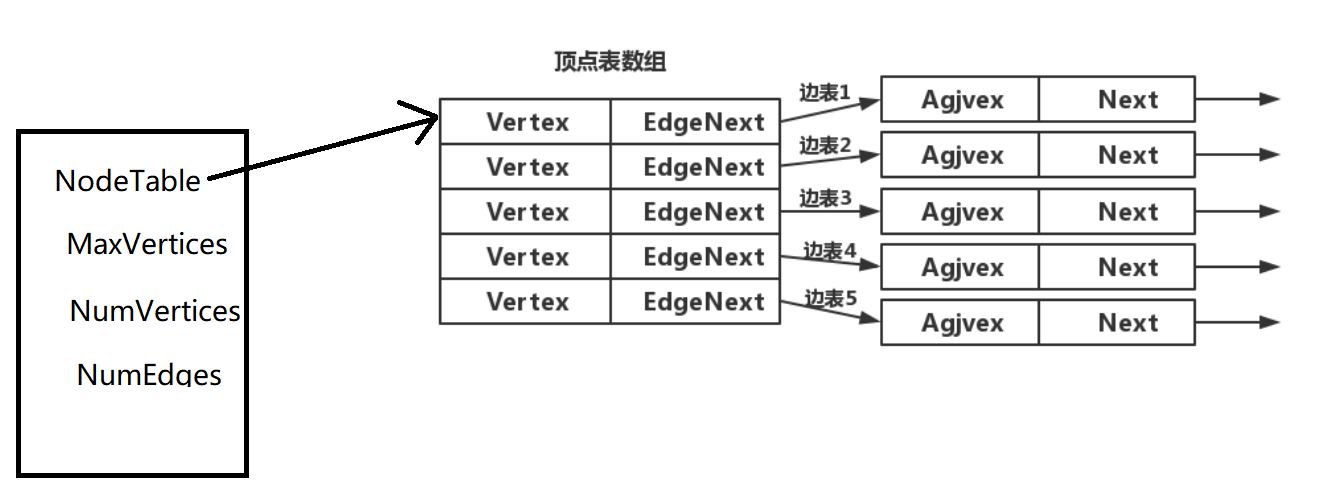
边表的头指针和顶点的数据信息采用顺序存储(称为顶点表)，所以在邻接表中存在两种结点：顶点表结点和边表结点，如下图所示：

链表的结点，没有先后顺序，都是直接连在顶点上的。所以链表有很多表示方式，不唯一。

一个参考图：

存储结构定义：

#define MaxVertexNum  100 //顶点数目最大值
typedef char VertexType;  //顶点的数据类型
typedef int EdgeType;     //带权图中边上权值的数据类型//边表结点
typedef struct EdgeNode{int adjvex;		        //该弧所指向的顶点的下标或者位置EdgeType weight;	    //权值，对于非网图可以不需要struct EdgeNode *next;	//指向下一个邻接点
}EdgeNode;//顶点表结点
typedef struct VertexNode{VertexType data;	    //顶点域，存储顶点信息EdgeNode *firstedge;	//边表头指针
}VertexNode, AdjList[MaxVertexNum];//邻接表
typedef struct{AdjList adjList;int vexnum, edgenum;		//图的当前顶点数和边数/弧数
}LinkGraph;

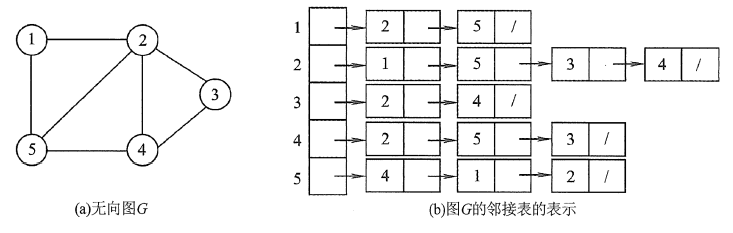
2.1无向图

无向图存储中，一条边会出现在两端点的链表中，边结点的数量是2|E|，整体空间复杂度为 O(|V|+ 2|E|)。

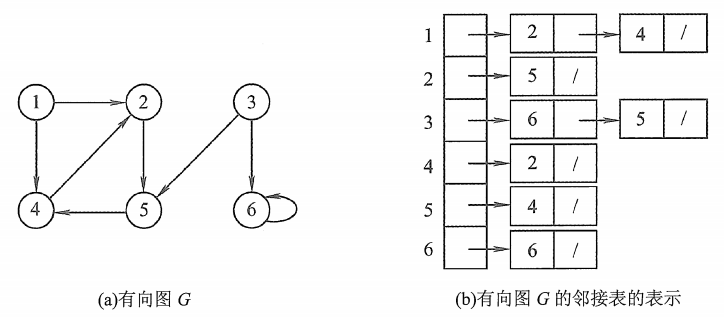
2.2有向图

有向图存储中，边结点的数量是|E|，整体空间复杂度为 O(|V|+ |E|)。

❗邻接表-C

/* 图邻接表(Adjacency List)存储方式是结合了 顺序存储 + 链式存储方法，减少了邻接矩阵不必要的浪费。无向图 与 有向图 的区别：就是一条edge是否添加两次到两端节点这里默认是无向图，但是在代码中注释了有向图C实现
*/#include <stdio.h>
#include <string.h>
#include <stdlib.h>#define MaxVertexNum  100 //顶点数目最大值
typedef char VertexType;  //顶点的数据类型
typedef int EdgeType;     //带权图中边上权值的数据类型#define numVertexes 5   // 顶点个数，用于visited数组
#define numEdges 7      // 边个数//边表结点
typedef struct EdgeNode{int adjvex;		        //该弧所指向的顶点的下标或者位置EdgeType weight;	    //权值，对于非网图可以不需要struct EdgeNode *next;	//指向下一个邻接点
}EdgeNode;//顶点表结点
typedef struct VertexNode{VertexType data;	    //顶点域，存储顶点信息EdgeNode *firstedge;	//边表头指针
}VertexNode, AdjList[MaxVertexNum];
// AdjList[MaxVertexNum]是静态的链表//邻接表
typedef struct{AdjList adjList;int vexnum, edgenum;		//图的当前顶点数和边数/弧数
}LinkGraph;void create_Graph(LinkGraph *G);
void create_Graph_ByArray(LinkGraph *G, int edges[][3]);
void print_Graph(LinkGraph G);int main()
{LinkGraph G;// 创建图方法1// create_Graph(&G);// 创建图方法2// 这里可以使用int，因为edge的EdgeType是intint edges[numEdges][3] = {  // 边的起点序号，终点序号，权值{1,2,1},{1,5,1},{2,3,1},{2,4,1},{2,5,1},{3,4,1},{4,5,1}};create_Graph_ByArray(&G,edges);print_Graph(G);return 0;
}// 创建图
void create_Graph(LinkGraph *G){int i, j;int start, end;  //边的起点序号、终点序号int w;   //边上的权值// 所创建图的顶点数和边数(用空格隔开)。这里也可以输入G->vexnum = numVertexes;G->edgenum = numEdges;printf("\n");//初始化顶点for (i=0; i<G->vexnum; i++){G->adjList[i].data = i+1;  //顶点初始化G->adjList[i].firstedge = NULL;  //边表头指针初始化为空}//初始化边for (i=0; i<G->edgenum; i++){printf("请输入边的起点序号，终点序号，权值(用空格隔开)(int,从1开始,没有0)：");scanf("%d%d%d", &start, &end, &w);// 创建边表结点// 有向图，只需要创建一个结点EdgeNode *e = (EdgeNode*)malloc(sizeof(EdgeNode));e->adjvex = end-1;  //终点序号e->weight = w;//将结点e插入顶点表start的边表中e->next = G->adjList[start-1].firstedge;G->adjList[start-1].firstedge = e;// 无向图，还要插入终点序号的边表//创建边表结点EdgeNode *e_ = (EdgeNode*)malloc(sizeof(EdgeNode));e_->adjvex = start-1;  //起点序号e_->weight = w;//将结点e_插入顶点表end的边表中e_->next = G->adjList[end-1].firstedge;G->adjList[end-1].firstedge = e_;}
}// 使用数组创建图
void create_Graph_ByArray(LinkGraph *G, int edges[][3]){int i, j;int start, end;  //边的起点序号、终点序号int w;   //边上的权值// 所创建图的顶点数和边数(用空格隔开)。这里也可以输入G->vexnum = numVertexes;G->edgenum = numEdges;printf("\n");//初始化顶点for (i=0; i<G->vexnum; i++){G->adjList[i].data = i+1;  //顶点初始化G->adjList[i].firstedge = NULL;  //边表头指针初始化为空}//初始化边for (i=0; i<G->edgenum; i++){start = edges[i][0];end = edges[i][1];w = edges[i][2];// 创建边表结点// 有向图，只需要创建一个结点EdgeNode *e = (EdgeNode*)malloc(sizeof(EdgeNode));e->adjvex = end-1;  //终点序号e->weight = w;//将结点e插入顶点表start的边表中e->next = G->adjList[start-1].firstedge;G->adjList[start-1].firstedge = e;// 无向图，还要插入终点序号的边表//创建边表结点EdgeNode *e_ = (EdgeNode*)malloc(sizeof(EdgeNode));e_->adjvex = start-1;  //起点序号e_->weight = w;//将结点e_插入顶点表end的边表中e_->next = G->adjList[end-1].firstedge;G->adjList[end-1].firstedge = e_;}
}// 输出图
void print_Graph(LinkGraph G){int i, j;printf("\n图的顶点为:");for (i=0; i<G.vexnum; i++){printf("%d ", G.adjList[i].data);}// 输出邻接表printf("\n图的邻接矩阵为:\n");for (i=0; i<G.vexnum; i++){		//遍历顶点printf("%d. %d:> ",i, G.adjList[i].data);	//输出顶点EdgeNode *p = G.adjList[i].firstedge;	//边结构while (p){							//遍历边printf("%d-->", p->adjvex+1);p = p->next;}printf("Null.\n");}
}

图的顶点为:1 2 3 4 5
图的邻接矩阵为:

0. 1:> 5–>2–>Null.
1. 2:> 5–>4–>3–>1–>Null.
2. 3:> 4–>2–>Null.
3. 4:> 5–>3–>2–>Null.
4. 5:> 4–>2–>1–>Null.

邻接矩阵VS邻接表

	邻接矩阵	邻接表
空间复杂度	O( IVI2 )	无向图O(|V|+2|E|)； 有向图O(|V|+|E|)。
适用于	稠密图	稀疏图
表示方式	唯一	不唯一
计算度、出度、入度	必须遍历对应的行或列	计算有向图的度、入度不方便，其余很方便。
找相邻的边	必须遍历对应的行或列	找有向图的入边不方便，其余很方便。
删除边、结点	删除边很方便，删除结点要移动大量数据	删除边、结点都不方便

邻接矩阵

1. 在简单应用中，可直接用二维数组作为图的邻接矩阵（顶点信息等均可省略）。
2. 当邻接矩阵中的元素仅表示相应的边是否存在时，EdgeType可定义为值为0和1的枚举类型或者bool。
3. 无向图的邻接矩阵是对称矩阵，对规模特大的邻接矩阵可采用压缩存储。
4. 邻接矩阵表示法的空间复杂度为O(n²)，其中n为图的顶点数|V|。
5. 用邻接矩阵法存储图，很容易确定图中任意两个顶点之间是否有边相连。但是，要确定图中有多少条边，则必须按行、按列对每个元素进行检测，所花费的时间代价很大。
6. 稠密图适合使用邻接矩阵的存储表示。

邻接表

1. 对于稀疏图，采用邻接表表示将极大地节省存储空间。

2. 在邻接表中，给定一顶点，能很容易地找出它的所有邻边，因为只需要读取它的邻接表。在邻接矩阵中，相同的操作则需要扫描一行，花费的时间为O(n)。
   但是，若要确定给定的两个顶点间是否存在边，则在邻接矩阵中可以立刻查到，而在邻接表中则需要在相应结点对应的边表中查找另一结点，效率较低。

3. 在有向图的邻接表表示中，
   求一个给定顶点的出度只需计算其邻接表中的结点个数；
   但求其顶点的入度则需要遍历全部的邻接表。

   因此，也有人采用逆邻接表的存储方式来加速求解给定顶点的入度。当然，这实际上与邻接表存储方式是类似的。

4. 图的邻接表表示并不唯一，因为在每个顶点对应的单链表中，各边结点的链接次序可以是任意的，它取决于建立邻接表的算法及边的输入次序。