【数学分析笔记】第1章第1节:集合(1)
作为一个计算机专业的人,想自学一下数学专业的专业课补一补AI基础,顺带写个笔记,听的课是陈纪修版本的数学分析:
1. 集合与映射
1.1 集合
1.1.1 基本概念
-
集合:由某种特定性质的具体的或抽象的对象汇集的总体。
-
集合的元素:集合中的“对象”又称为集合的元素。
-
集合往往是用大写字母表示,比如 S , T , A , B , X , Y \textbf{S},\textbf{T},\textbf{A},\textbf{B},\textbf{X},\textbf{Y} S,T,A,B,X,Y;
-
对元素来说往往是用小写字母表示,比如
s , t , a , b , x , y s,t,a,b,x,y s,t,a,b,x,y; -
x x x是集合 S S S的元素,记为 x ∈ S x\in \textbf{S} x∈S
-
y y y不是集合 S S S的元素,记为 y ∈ ˉ S y\bar \in \textbf{S} y∈ˉS或 y ∉ S y\notin \textbf{S} y∈/S
1.1.2 常见的集合
常见的集合表示如下:
| 类型 | 符号 | 说明 |
|---|---|---|
| 正整数集合 | N + \textbf{N}^{+} N+ | { 1 , 2 , 3 , . . . } \{1,2,3,...\} {1,2,3,...} |
| 自然数集合 | N \textbf{N} N | { 0 , 1 , 2 , . . . } \{0,1,2,...\} {0,1,2,...} |
| 整数集合 | Z \textbf{Z} Z | { . . . , − 1 , 0 , 1 , . . . } \{...,-1,0,1,...\} {...,−1,0,1,...} |
| 有理数集合 | Q \textbf{Q} Q | 有理数是整数(正整数、0、负整数)和分数的统称,是整数和分数的集合 |
| 实数集合 | R \textbf{R} R | 实数是有理数和无理数的总称 |
| 空集 | ∅ \emptyset ∅ | 没有任何元素的集合 |
1.2 集合的表示
1.2.1 枚举法
所谓枚举法就是将集合中的元素一个一个写出来。
【例】光的基色的集合
{ 红 , 绿 , 蓝 } \{红,绿,蓝\} {红,绿,蓝}
【例】 A \textbf{A} A是 a , b , c , d a,b,c,d a,b,c,d构成的集合
A = { a , b , c , d } \textbf{A}=\{a,b,c,d\} A={a,b,c,d}
【例】整数集合
Z = { ± 1 , ± 2 , . . . , ± n , . . . } \textbf{Z}=\{\pm 1,\pm 2,...,\pm n,...\} Z={±1,±2,...,±n,...}
【例】正整数集合
N + = { 1 , 2 , 3 , . . . , n , . . . } \textbf{N}^{+}=\{1,2,3,...,n,...\} N+={1,2,3,...,n,...}
1.2.2 描述法
一个集合是具有某种性质 p p p元素汇集的总体, S = { x ∣ x 满足性质 p } \textbf{S}=\{x|x满足性质p\} S={x∣x满足性质p},像这样一个描述集合的方法叫做描述法
【例】2的方根
{ x ∣ x 2 = 2 } \{x|x^{2}=2\} {x∣x2=2}
【例】有理数集合
Q = { x ∣ x = q p , p ∈ N + 且 q ∈ Z } \textbf{Q}=\{x|x=\frac{q}{p},p\in \textbf{N}^{+}且q\in \textbf{Z}\} Q={x∣x=pq,p∈N+且q∈Z}
【注】(1)集合的表示中没有次序的关系,比如, { a , b } = { b , a } \{a,b\}=\{b,a\} {a,b}={b,a};重复也是有意义的(重复的元素相当于一个元素), { a , b } = { b , a } = { a , a , b } \{a,b\}=\{b,a\}=\{a,a,b\} {a,b}={b,a}={a,a,b}
(2)空集的概念:没有元素的集合称为空集,比如, C = { x ∈ R 且 x 2 = − 1 } = ∅ \textbf{C}=\{x\in \textbf{R}且x^{2}=-1\}=\emptyset C={x∈R且x2=−1}=∅或 C = { x ∈ R 且 x 2 + 1 = 0 } = ∅ \textbf{C}=\{x\in \textbf{R}且x^{2}+1=0\}=\emptyset C={x∈R且x2+1=0}=∅
相关文章:
)
【数学分析笔记】第1章第1节:集合(1)
作为一个计算机专业的人,想自学一下数学专业的专业课补一补AI基础,顺带写个笔记,听的课是陈纪修版本的数学分析: 1. 集合与映射 1.1 集合 1.1.1 基本概念 集合:由某种特定性质的具体的或抽象的对象汇集的总体。 集…...

计算机毕业设计 校园失物招领网站 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

GIT指令大全详解
目录 GIT指令详解 拉取 提交 分支操作(假设分支为a) 版本回退 主分支拉取到分支 常用的Git指令 一、初始化配置 二、初始化仓库 三、检查当前文件状态 四、添加 五、查看提交历史 六、撤销更改 七、查询 八、分支 九、标签管理 十、其他常用指令 GIT指令详解 Git是一个开源的分…...

ECCV2024,清华百度提出ReSyncer:可实现音频同步嘴唇动作视频生成。
清华&百度等联合提出了ReSyncer,可以实现更高稳定性和质量的口型同步,而且还支持创建虚拟表演者所必需的各种有趣属性,包括快速个性化微调、视频驱动的口型同步、说话风格的转换,甚至换脸。 ReSyncer的工作原理可以简单理解为…...

论文笔记:YOLOv8-QSD 自动驾驶场景小目标检测算法
摘要 YOLOv8-QSD网络是一种新型的无锚点驾驶场景检测网络,建立在YOLOv8的基础上,在保证检测精度的同时保持效率。该网络的骨干网采用结构重参数化技术来转换基于多样化分支块 (DBB) 的模型。 为了准确检测小目标,它集…...

Vue.js状态管理:Vuex与Pinia的比较
在 Vue.js 生态系统中,状态管理是构建复杂应用时的重要组成部分。Vue.js 提供了两种流行的状态管理库:Vuex 和 Pinia。虽然两者都旨在简化状态管理,但它们在设计哲学、API、性能和易用性方面有所不同。本文将深入探讨 Vuex 和 Pinia 的异同&a…...

OJ题目【栈和队列】
目录 有效的括号 有效的括号【代码】 用队列实现栈 用队列实现栈【代码】 用栈实现队列 用栈实现队列【代码】 设计循环队列 有效的括号 https://leetcode.cn/problems/valid-parentheses/submissions/551394950/ 思路:把左括号放到栈里,取出来栈…...

[shell][git]git将当前分支的HEAD指针重置到最后一次提交的状态
在Git中,git reset --hard HEAD 命令用于将当前分支的HEAD指针重置到最后一次提交的状态,并且会丢弃当前工作目录中的所有更改。这个命令的意思是: git reset:重置命令,用于将HEAD指针移动到指定的状态。--hard&#…...
卡尔曼滤波器二:图解卡尔曼滤波器;卡尔曼滤波器公式理解;面试答法;)
高翔【自动驾驶与机器人中的SLAM技术】学习笔记(六)卡尔曼滤波器二:图解卡尔曼滤波器;卡尔曼滤波器公式理解;面试答法;
上一篇卡尔曼滤波器一中,从整体上认识了,卡尔曼滤波器整体是在做一件什么事。 知道了,协方差就可以理解为偏差,或者误差。 这一篇主要讲卡尔曼滤波器中的公式,理解公式,就能知道如何实现卡尔曼滤波器。 上一篇:卡尔曼滤波器在做一件什么事,这一篇,卡尔曼滤波器怎么…...

高性能日志系统 日志输出模块逻辑
概述 该模块主要实现了一个日志系统的输出模块,通过多态、工厂模式等设计模式,构建灵活的日志输出架构。 功能:格式化完成的标准日志消息,输出到指定为止拓展:支持同时将日志落地到不同的位置,也就是输出日…...

haproxy基础
目录 1 HAProxy介绍 1.1 版本对比 1.2 HAProxy功能 2 参数介绍与实践 2.1 global参数说明 2.2 真实代码格式实例 2.3 常用全局参数 2.3.1 nbproc -- 开启几个进程 2.3.2 cpu-map(CUP绑定) 2.3.3 nbthread 2 --开启2个线程 3 Proxies配置 3.1 Proxies配置-defaults 3.2 Proxi…...

C++ 面试题常用总结 详解(满足c++ 岗位必备,不定时更新)
📚 本文主要总结了一些常见的C面试题,主要涉及到语法基础、STL标准库、内存相关、类相关和其他辅助技能,掌握这些内容,基本上就满足C的岗位技能(红色标记为重点内容),欢迎大家前来学习指正&…...

LVS实验——部署DR模式集群
目录 一、实验环境 二、配置 1、LVS 2、router 3、client 4、RS 三、配置策略 四、测试 1.Director服务器采用双IP桥接网络,一个是VPP,一个DIP 2.Web服务器采用和DIP相同的网段和Director连接 3.每个Web服务器配置VIP 4.每个web服务器可以出外网…...
pythonUI自动化008::allure测试报告(安装及应用)
allure报告预览 1 下载jdk,配置jdk Path变量: https://www.cnblogs.com/FBGG/p/15103119.html(这里不作阐述,请看该偏文章配置即可) 2 下载allure驱动,配置allure Path变量: 下载allure驱动&a…...

常用的 git 和 linux 命令有哪些?
对于 Git 命令: 1. git init:初始化一个新的 Git 仓库。 2. git clone:克隆一个远程仓库到本地。 3. git add:将文件添加到暂存区。 4. git commit:提交暂存区的更改。 5. git status:查看工作区和暂存…...

MYSQL 删除一个字段前,判断字段是否存在
开发过程中经常需要提交可以重复执行的sql,当设计到需要增加字段时,可以参考如下办法: 1.如果是mysql 版本高于5.7.5 ALTER TABLE table_name DROP COLUMN IF EXISTS column_name; 2.通用方法 写一个存储过程,然后用存储过程取…...

vulnstack-5
环境搭建 靶场虚拟机共用两个,一个外网一个内网,用来练习红队相关内容和方向,主要包括常规信息收集、Web攻防、代码审计、漏洞利用、内网渗透以及域渗透等相关内容学习。 虚拟机密码 win7 sun\heart 123.com sun\Administrator dc123.com # …...

回归预测|基于灰狼优化GWO-Transformer-BiLSTM组合模型的数据回归预测Matlab程序 多特征输入单输出
回归预测|基于灰狼优化GWO-Transformer-LSTM组合模型的数据回归预测Matlab程序 多特征输入单输出 文章目录 前言回归预测|基于灰狼优化GWO-Transformer-BiLSTM组合模型的数据回归预测Matlab程序 多特征输入单输出GWO-Transformer-BiLSTM 一、GWO-Transformer-BiLSTM模型二、实验…...

STM32的USB接口介绍
STM32 USB接口是STM32微控制器系列中集成的一种通信接口,它允许STM32微控制器与外部设备或计算机进行高速的数据传输和通信。以下是STM32 USB接口的简要介绍: 1. 接口类型 STM32的USB接口通常支持USB 2.0标准,部分高端型号可能还支持USB 3.…...

【中等】 猿人学web第一届 第2题 js混淆 动态cookie 1
目录 调试干扰Hook Function 加密参数定位hook Cookie AST 解混淆字符串解密还原解密函数AST 配合解密函数还原字符串 ASCII 编码字符串还原字符串相加花指令(对象)剔除无用代码虚假 if剔除无引用代码剔除无引用的对象数值还原 switch 还原完整的 AST 代码代码注意 还原加密 请…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
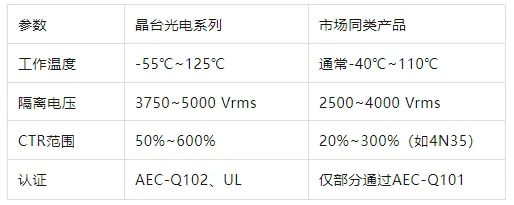
高抗扰度汽车光耦合器的特性
晶台光电推出的125℃光耦合器系列产品(包括KL357NU、KL3H7U和KL817U),专为高温环境下的汽车应用设计,具备以下核心优势和技术特点: 一、技术特性分析 高温稳定性 采用先进的LED技术和优化的IC设计,确保在…...

Qt学习及使用_第1部分_认识Qt---Qt开发基本流程
前言 学以致用,通过QT框架的学习,一边实践,一边探索编程的方方面面. 参考书:<Qt 6 C开发指南>(以下称"本书") 标识说明:概念用粗体倾斜.重点内容用(加粗黑体)---重点内容(红字)---重点内容(加粗红字), 本书原话内容用深蓝色标识,比较重要的内容用加粗倾…...

分布式光纤声振传感技术原理与瑞利散射机制解析
分布式光纤传感技术(Distributed Fiber Optic Sensing,简称DFOS)作为近年来迅速发展的新型感知手段,已广泛应用于边界安防、油气管道监测、结构健康诊断、地震探测等领域。其子类技术——分布式光纤声振传感(Distribut…...

React与原生事件:核心差异与性能对比解析
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
