记忆化搜索专题篇

目录
斐波那契数
不同路径
最长递增子序列
猜数字大小II
矩阵中的最长递增路径
声明:下面将主要使用递归+记忆化搜索来解决问题!!!
斐波那契数
题目

思路
斐波那契数的特点就是除了第一个数是0,第二个数是1,其余的数都是前两个数的和。
显然我们很容易用递归实现,但是会超时的,因为计算第n个位置的斐波那契数的大小时,会重复很多次的计算某些位置的斐波那契数,因此如果我们能记录下已经计算过的位置对应的斐波那契数时,当再次需要该位置的斐波那契数时,就不用再重复的进行计算了。
代码
class Solution {long long memo[101];
public:int fib(int n) {memset(memo,-1,sizeof memo);// std::fill(memo, memo + 101, -1);return dfs(n);}int dfs(int n){if(memo[n]!=-1)return memo[n];if(n==0 || n==1){memo[n]=n;return memo[n];}memo[n]=(dfs(n-1)+dfs(n-2))%1000000007;return memo[n];}
};class Solution {
// public:
// int fib(int n) {
// if(n==0 || n==1)
// return n;
// vector<int> dp(n+1);
// dp[0]=0,dp[1]=1;
// for(int i=2;i<=n;i++)
// dp[i]=(dp[i-1]+dp[i-2])%1000000007;
// return dp[n];
// }
// };不同路径
题目

思路
本道题很容易使用递归实现,但是会超时,原因同上一道题一样,会大量重复的计算一些以某些位置为起点到终点的路径数,而且时间复杂度是呈指数级别的,因此,我们可以和上一道题一样,如果将已经计算过的以某些位置为起点到终点的路径数记录下来,当再次求以这些位置为起点到终点的路径数时,直接使用即可,避免了大量的重复计算。
代码
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> memo(m+1,vector<int>(n+1));return dfs(m,n,memo);}int dfs(int x,int y,vector<vector<int>>& memo){if(memo[x][y]!=0) return memo[x][y];if(x==0|| y==0) return 0;if(x==1 && y==1){memo[x][y]=1;return 1;}else{memo[x][y]=dfs(x-1,y,memo)+dfs(x,y-1,memo);return memo[x][y];}}
};class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m+1,vector<int>(n+1));// dp[0][1]=1;dp[1][0]=1;for(int i=1;i<=m;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j]+dp[i][j-1];}}return dp[m][n];}
};最长递增子序列
题目

思路
这道题已经在之前的博客中写过了,之前使用的是动态规划和贪心+二分,之前的动态规划是从前往后分析的,下面将使用递归+记忆化搜素,以及从后往前的分析的动态规划。
递归+记忆化搜素
从头到尾扫描数组,分别计算以该位置为起点的最长递增子序列的长度,并把每次计算好的结果进行记录,当下次再次用到以已记录位置为起点的最长递增子序列的长度时,直接拿已经计算好的结果即可,避免了不少重复的计算。
从后往前的分析的动态规划
可以说是在分析前面的递归+记忆化搜素方法的基础上摸索出来的,如何定义状态表示和状态转移方程等,这里不再赘述,可以参考之前的博客。
代码
class Solution {
public:int lengthOfLIS(vector<int>& nums) {//记忆化搜索int ret=1;vector<int> memo(nums.size());for(int i=0;i<nums.size();i++)ret=max(ret,dfs(i,nums,memo));return ret;}int dfs(int pos,vector<int>& nums,vector<int>& memo){if(memo[pos]!=0) return memo[pos];int k=1;for(int i=pos+1;i<nums.size();i++)if(nums[i]>nums[pos])k=max(k,dfs(i,nums,memo)+1);memo[pos]=k;return k;}
};//递归+记忆化搜素 class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n=nums.size();vector<int> dp(n,1);for(int i=n-1;i>=0;i--)for(int j=i+1;j<n;j++){if(nums[i]<nums[j])dp[i]=max(dp[i],dp[j]+1);}return *max_element(dp.begin(),dp.end());}
};//动态规划猜数字大小II
题目

思路
上面之所以没有截示例,是因为示例比较长,而且文字描述很多,比较容易看晕,下面也是采用递归+记忆化搜素来解决,因为如果只使用递归会超时,因为会大量的重复计算相同位置的值,如果能够将每次计算好的值保存起来,下次使用时直接取,就能够较少大量的操作,更佳。
从头到尾扫描整个数组,分别计算以该位置为起点的最大花费,然后计算所有起始位置的最大花费的最小值。
代码
class Solution {int memo[201][201];
public:int getMoneyAmount(int n) {return dfs(1,n);}int dfs(int left,int right){if(left>=right) return 0;if(memo[left][right]!=0) return memo[left][right];int ret=INT_MAX;for(int head=left;head<=right;head++){int x=dfs(left,head-1);int y=dfs(head+1,right);ret=min(ret,head+max(x,y));}memo[left][right]=ret;return ret;}
};矩阵中的最长递增路径
题目


思路
下面也是采用递归+记忆化搜素来解决,因为如果只使用递归会超时,因为会大量重复计算以某位置为起点的最长递增路径,如果能够记录下以某位置为起点的最长递增路径,当下次使用时直接取即可,就能够减少大量的重复计算,以示例1为例,比如就以【2】【1】位置的1为起始位置,计算时会有一条向上到6的路径,但是如果已经计算过以这个6为起始位置的最长递增路径的长度,可以直接使用,就不用再重复计算了。

代码
class Solution {
public:int n,m;int maxlen[201][201];int dx[4]={0,0,1,-1};int dy[4]={1,-1,0,0};int longestIncreasingPath(vector<vector<int>>& matrix) {int ret=0;n=matrix.size(),m=matrix[0].size();for(int i=0;i<n;i++)for(int j=0;j<m;j++)ret=max(ret,dfs(matrix,i,j));return ret;}int dfs(vector<vector<int>>& matrix,int i,int j){if(maxlen[i][j]!=0) return maxlen[i][j];int ret=1;for(int k=0;k<4;k++){int x=i+dx[k];int y=j+dy[k];if(x>=0 && x<n && y>=0 && y<m && matrix[x][y]>matrix[i][j])ret=max(ret,dfs(matrix,x,y)+1);}maxlen[i][j]=ret;return ret;}
};相关文章:

记忆化搜索专题篇
目录 斐波那契数 不同路径 最长递增子序列 猜数字大小II 矩阵中的最长递增路径 声明:下面将主要使用递归记忆化搜索来解决问题!!! 斐波那契数 题目 思路 斐波那契数的特点就是除了第一个数是0,第二个数是1&…...

入网测评检查项大全(安全资料)
1. Linux操作系统 2. Windows操作系统 3. Tomcat中间件 4. Nginx中间件 5. Mysql数据库 6. Weblogic中间件 7. Oracle数据库 8. Redis数据库 9. 达梦数据库 10. 应用系统 11. 渗透测试 13 .AIX操作系统 14 .中创中间件 15 .IIS中间件 16 .Apache中间件 17 .Mari…...
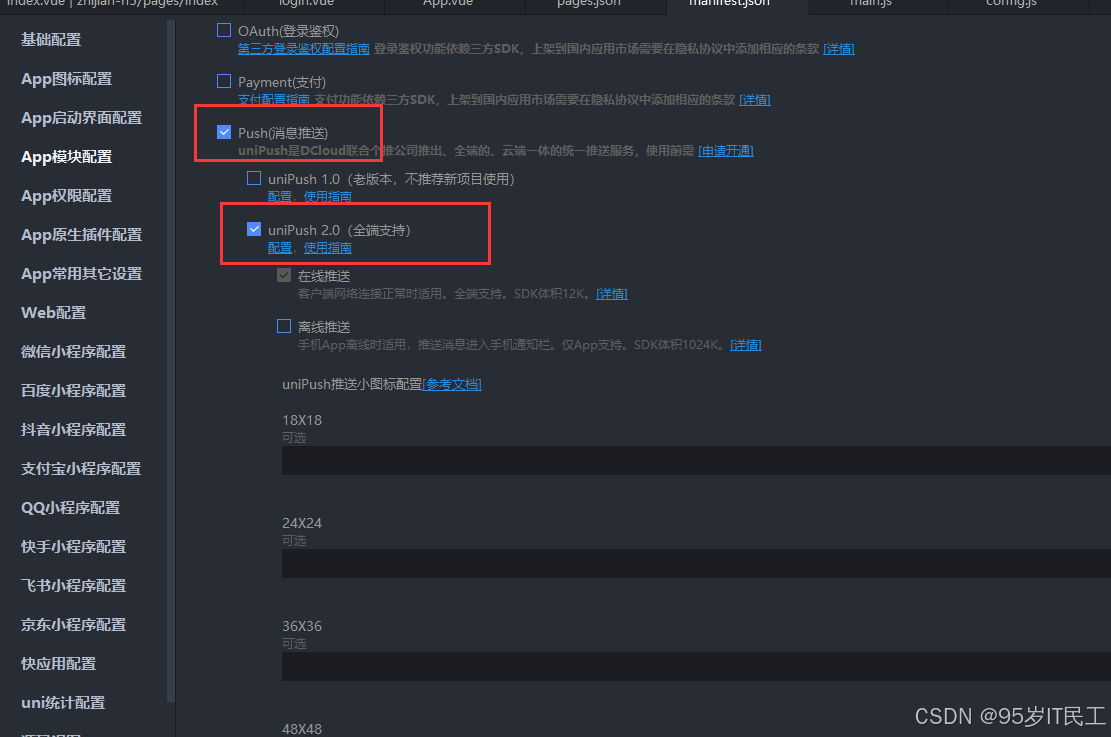
uni-app 开发App时调用uni-push 实现在线系统消息推送通知 保姆教程
一、引言 在开发App时避免不了需要推送系统通知,以提高用户的使用体验。在自己的一个工具型的小app上全流程接入了uni-push2.0的推送能力,做个记录,以防后期需要用到。在阅读本教程前最好先看看官方文档,结合官方文档使用…...

13.StringRedisTemplete使用
上一篇说到改变了RedisTemplate的默认序列化器后,在redis中存入Java对象后,在redis中的呈现是:会记录类的字节码 这也是代码中可以强制装换为对应的java对象的原因: Test void testStudent() {redisTemplate.opsForValue().set(&q…...

[工具]-gitee+pycharm-配置
安装git 查看git是否安装设置成功: git config user.name git config user.email 码云账号设置邮箱 pycharm设置gitee 打开 PyCharm,在 Settings - Plugins 里面,搜索 Gitee 插件,安装后重启 PyCharm。 pychar…...

中间件是一种在客户端和服务器之间进行通信和处理的软件组件或服务
中间件是一种在客户端和服务器之间进行通信和处理的软件组件或服务。中间件位于应用程序和操作系统之间,可以提供一些功能,如请求转发、数据转换、安全性和身份验证、日志记录等。 中间件的主要作用是将应用程序与底层基础设施解耦,提供了一…...

RCE-eval长度限制突破技巧
目录 一、长度17的限制绕过 1、最简单的绕过 (一)绕过 (二)编写一句话木马 2、文件包含的利用 (一)远程文件包含的利用 (二)本地文件包含的利用 3、usort绕过 (…...

【黑马】MyBatis
目录 MyBatis简介JDBC缺点:MyBatis针对于JDBC进行简化,简化思路: MyBatis快速入门具体构建步骤解决SQL映射文件的警告提示 Mapper代理开发案例:使用Mapper代理方式完成案例具体步骤详解:Mapper代理方式 Mapper核心配置…...

oracle创建dblink使得数据库A能够访问数据库B表LMEAS_MFG_FM的数据
1、给数据库A普通用户CMRONLINE相应的权限,在sys用户下执行以下语句 GRANT CREATE DATABASE LINK TO CMRONLINE; GRANT DROP PUBLIC DATABASE LINK TO CMRONLINE; GRANT CREATE PUBLIC DATABASE LINK TO CMRONLINE; 2、在数据库A用户 CMRONLINE下执行创建语句&…...

git config 如何配置用户账户
Git配置用户账户主要涉及设置用户名和邮箱地址,这是Git进行版本控制时用于标识提交者身份的重要信息。以下是如何配置Git用户账户的详细步骤: 1. 打开命令行工具 首先,需要打开命令行工具(如CMD、Terminal或Git Bash等ÿ…...

SpringBoot基础(二):配置文件详解
SpringBoot基础系列文章 SpringBoot基础(一):快速入门 SpringBoot基础(二):配置文件详解 目录 一、配置文件分类二、配置文件优先级1、不同版本优先级2、不同位置优先级 三、配置文件格式1、yml和yaml格式1.1、字符串1.2、布尔类型1.3、整数型1.4、浮点…...

Web安全(一)-靶场搭建过程-基于docker
今天来复习一下web方面的知识 1.1 sqliab环境搭建 基于Centos 和Docker 1.1.1 Vmware环境安装 这个就略去了吧 博主使用的是vmware17pro 具体的密钥什么的大家懂的都懂 这里就不提供了 接下来 将带大家安装centos7的镜像 为了方便操作 这里选择 centos7_minimal 地址如下:…...

【JavaEE】单例模式和阻塞队列
🔥个人主页: 中草药 🔥专栏:【Java】登神长阶 史诗般的Java成神之路 🕯️一.设计模式 在Java中,设计模式(Design Patterns)是指在软件工程和面向对象编程中,针对特定…...

RCE绕过技巧
目录 EVAL长度限制突破技巧 1.使用反引号 2.file_put_contents写入文件 3.php5.6变长参数usort回调后门 命令长度限制突破技巧 1.拼接文件名 无字母数字的webshell命令执行 1.取反码 2.上传临时文件 EVAL长度限制突破技巧 分析代码:首先传递一个param参数&…...

Spring源码解析(31)之事务配置文件解析以及核心对象创建过程
一、前言 首先我们先准备一下spring 事务的配置文件,具体内容如下: <?xml version"1.0" encoding"UTF-8"?> <beans xmlns"http://www.springframework.org/schema/beans"xmlns:xsi"http://www.w3.org/20…...

win11安装docker报错记录
报错一: Docker Desktop - Unexpected WSL error An unexpected error occurred while executing a WSL command. Either shut down WSL down with wsl --shutdown, and/or reboot your machine. You can also try reinstalling WSL and/or Docker Desktop. If t…...
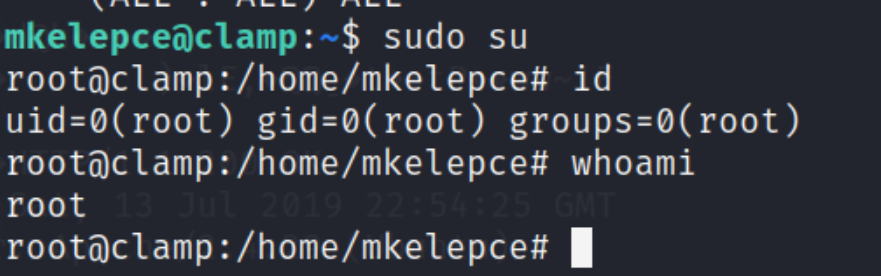
【vulnhub】CLAMP 1.0.1靶机
信息收集 靶机发现 端口扫描 页面访问,并查看源码 访问 /nt4stopc/,下面有一些问题,提示必须收集答案 一些判断题,对与错对应1与0,最后结果为0110111001,拼接访问 点击图中位置,发现存在参数,p…...

GPS跟踪环路MATLAB之——数字锁相环
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 GPS跟踪环路MATLAB之——数字锁相环 前言为什么要锁相环科斯塔斯环锁相环的一些基本概念1、捕获、锁定与跟踪的概念2、捕获时间和稳态相差3、相位捕获和频率捕获4、捕获带和同…...

docker开发环境搭建-关于数据库的IP是什么
故事的背景是这样的: 我在本地的ubuntu系统上安装了docker,并创建了一个mysql容器,但是在使用DBeaver连接该数据库时,需要填写数据库的ip,填写127.0.0.1,工具提示找不到这个库,然后使用ip addr…...

loginApi
import request from "/utils/request"; import { AxiosPromise } from "axios"; import { CaptchaResult, LoginData, LoginResult } from "./types";/*** 登录API** param data {LoginData}* returns*/ export function loginApi(data: LoginD…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

数学建模-滑翔伞伞翼面积的设计,运动状态计算和优化 !
我们考虑滑翔伞的伞翼面积设计问题以及运动状态描述。滑翔伞的性能主要取决于伞翼面积、气动特性以及飞行员的重量。我们的目标是建立数学模型来描述滑翔伞的运动状态,并优化伞翼面积的设计。 一、问题分析 滑翔伞在飞行过程中受到重力、升力和阻力的作用。升力和阻力与伞翼面…...
