【整数规划】+【0—1规划】解决优化类问题(Matlab代码)
目录
文章目录
前言
一、整数规划
分类:
二、典例讲解
1.背包问题
2.指派问题
总结
前言
如果觉得本篇文章还不错的话,给作者点个赞鼓励一下吧😁😁😁
在规划问题中,有些最优解可能是分数或小数,但对于某些具体问题,常要求某些变量(全部或部分)的解必须是整数。例如当我们的变量时人数或者机器的台数。此时我们就需要利用整数规划来求最优解。
一、整数规划
分类:
- 🌏线性整数规划:我们只需要在线性规划的基础上,加入决策变量取整数的条件
此时我们使用matlab中的intlinprog函数,其中intcon中的值指示决策变量 x 中应取整数值的分量,其他都与线性规划的变量含义相同。如假如有x1,x2,x3三个整数变量则令intcon=[1,2,3]/[1:3]
- 🌏非线性整数规划:无特定算法,只能用近似算法 ,如蒙特卡罗模拟,智能算法
- 🌏0—1规划:仍然使用intlinprog函数求解,只需要限定lb和ub即可
如:假如有三个决策变量,其中x2,x3为0-1变量,而x1不限制,则 lb=[-inf(负无穷),0,0],ub=[+inf,1,1],每个决策变量的范围按照顺序一一对应
二、典例讲解
1.背包问题

通过读题我们很容易达到这是一个优化类题目,并且需要用到0-1整数规划,因为货物的运送只有运送(0)和不运送(1)两种情况,那么我们写出相应的目标函数和约束条件
这里我们可以设第i件物品为xi,其重量为wi,取得的利润为pi
则总利润:
约束条件:根据题干中所给条件写出
特别注意:运用intlinprog函数仍然要符合函数的使用形式,要把最大值的求解变成min,大于等于变成<=

然后我们只需要将根据上述所列设相应的变量并且带入函数即可
%背包问题
clear,clc
f = -[540,200,180,350,60,150,280,450,320,120];%特别注意要转换成求最小值
intcon= 1:10;%xi都是整数
A = [6,3,4,5,1,2,3,5,4,2];
b = 30;
lb=zeros(10,1);%约束变量的下届
ub=ones(10,1);%约束变量的上界
[x,favl] = intlinprog(f,intcon,A,b,[],[],lb,ub);%这里没有等式约束则Aeq,beq为[][]
W = -favl;%计算出最大利润
disp('选择运输的结果为:');disp(x);
disp('最大利润为:');disp(W);
2.指派问题
指派问题通常是将i人分配到j地,再对相应问题求解

注意: 当下标有两个变量时,我们需要将这些变量按照顺序排列起来,要从1开始重新给他们排列得到决策变量的相应下标,其他做法均与线性规划问题相同
%指派问题
%注意这里要把双指标转换成单指标,x11->x1,x12->2···x21-x5···,x54->x20
%目标函数的系数矩阵
f=[66.8,75.6,87,58.6,57.2,66,66.4,53,78,67.8,84.6,59.4,70,74.2,69.6,57.2,67.4,71,83.8,62.4];intcon=1:20;
%不等式约束的系数矩阵和常数项矩阵
A =[1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];
b=ones(5,1);
%等式约束
Aeq = repmat(eye(4),1,5);
beq = ones(4,1);
lb = zeros(20,1);
ub = ones(20,1);
%最后调用函数即可
[x,favl]=intlinprog(f,intcon,A,b,Aeq,beq,lb,ub);
disp('安排方式为');disp(x);
disp('最短的时间为');disp(favl);
x = reshape(x,4,5);%reshape函数会将原始向量中的数据将按照列的顺序填充到新的矩阵
disp(x');总结
完结撒花🎇🎆🎇🎆
背包问题和指派问题是运用0-1规划的常见两种情况,需要掌握还有其他一些情况大家可自行查找资料学习
相关文章:

【整数规划】+【0—1规划】解决优化类问题(Matlab代码)
目录 文章目录 前言 一、整数规划 分类: 二、典例讲解 1.背包问题 2.指派问题 总结 前言 如果觉得本篇文章还不错的话,给作者点个赞鼓励一下吧😁😁😁 在规划问题中,有些最优解可能是分数或小数&am…...

Linux下如何使用Curl进行网络请求
在Linux系统上,Curl是一个非常强大的网络请求工具,可以用于发送各种类型的HTTP请求,并获取响应结果。它支持常见的HTTP方法,如GET、POST、PUT、DELETE等,还支持HTTPS、FTP等不同协议。Curl提供了丰富的参数选项&#x…...

PostgreSQL 触发器
PostgreSQL 触发器 PostgreSQL触发器是一种强大的数据库对象,它可以在特定的数据库事件发生时自动执行预定义的操作。这些事件可以是插入、更新或删除表中的行。触发器通常用于强制复杂的业务规则、提供审计跟踪、数据同步以及实现复杂的约束。 触发器的基本概念 …...

LeetCode——3131.找出与数组相加的整数I
通过万岁!!! 题目:给你两个数组nums1和nums2,然后让你找一个数,使得nums1的数加上这个数以后得到的数组nums1’与nums2是相同的。注意这里只要元素相同就好了,不一定顺序相同。思路:…...

【SpringMVC】详细了解SpringMVC中WEB-INF 目录资源,视图解析器和静态资源放行的使用。
目录 1. 回顾SpringMVC请求转发和重定向 2. WEB-INF资源目录 3. 视图解析器 4. 静态资源放行 1. 回顾SpringMVC请求转发和重定向 概念:在一个项目中功能非常多,也就意味着有非常多的Servlet,不同的Servlet的职不 同 ,而用户发起…...

如何学好uni-app
学习uni-app需要掌握以下技能: 1. 前端基础:熟悉HTML、CSS和JavaScript等前端开发技术,了解基本的前端框架如Vue.js。 2. Vue.js:因为uni-app是基于Vue.js构建的,所以需要对Vue.js有深入的理解。可以先通过官方文档或者…...

C++ QT使用stackwidget实现页面切换(含源码)
C++ QT使用stackwidget实现页面切换(含源码) 0.前言1.UI布局1.1使用stackwidget2.代码方式添加页面实现页面切换3.源码4.最终效果0.前言 在QT中一个界面中如何实现页面的切换,而不是新弹出的窗口,这里采用的stackwidget,以层叠widget的方式选定页面索引从而实现页面切换。…...

打工人上班适合用的蓝牙耳机推荐?几款开放式耳机推荐
日常工作的话,我还是比较推荐开放式蓝牙耳机的,它特别适合那些需要在长时间工作中保持专注和舒适度的环境,那开放式耳机其实还有一些主要的优点: 减少耳朵疲劳:由于开放式耳机不需要紧密贴合耳朵,因此可以…...
一款.NET开发的AI无损放大工具
一款.NET开发的AI无损放大工具 思维导航 前言项目功能支持语言系统要求项目源代码项目运行小图片进行无损放大项目源码地址优秀项目和框架精选 前言 今天大姚给大家分享一款由.NET开源(GPL-3.0 license)、基于腾讯ARC Lab提供的Real-ESRGAN模型开发的A…...

编程新手必看:彻底理解!与~的取反操作
在编程和计算机科学的语境中,! 和 ~ 都是取反操作符,但它们的应用方式和效果存在显著的区别。下面将从定义、应用场景、作用原理及示例等方面对 ! 和 ~ 进行详细解析。 一、定义 !(逻辑非运算符) 在C语言、Java等多数编程语言中&…...

【LeetCode】54. 螺旋矩阵
螺旋矩阵 题目描述: 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:[1,2,3,6,9,8,7,4,5]示例 2:…...

计算机毕业设计 奖学金评定管理系统 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

【JavaWeb项目】——外卖订餐系统之商家添加餐品、修改餐品、查询热卖餐品、查询出售车、进行发货操作
🎼个人主页:【Y小夜】 😎作者简介:一位双非学校的大二学生,编程爱好者, 专注于基础和实战分享,欢迎私信咨询! 🎆入门专栏:🎇【MySQL࿰…...

制作抖音私信卡片 - 一键调起并跳转微信二维码
抖音私信图文卡片,点击可以直接一键添加微信 可生成无风险链接,使用苹果手机转发创建出卡片 抖音内点击可以直接调起微信跳入小程序展示微信二维码...
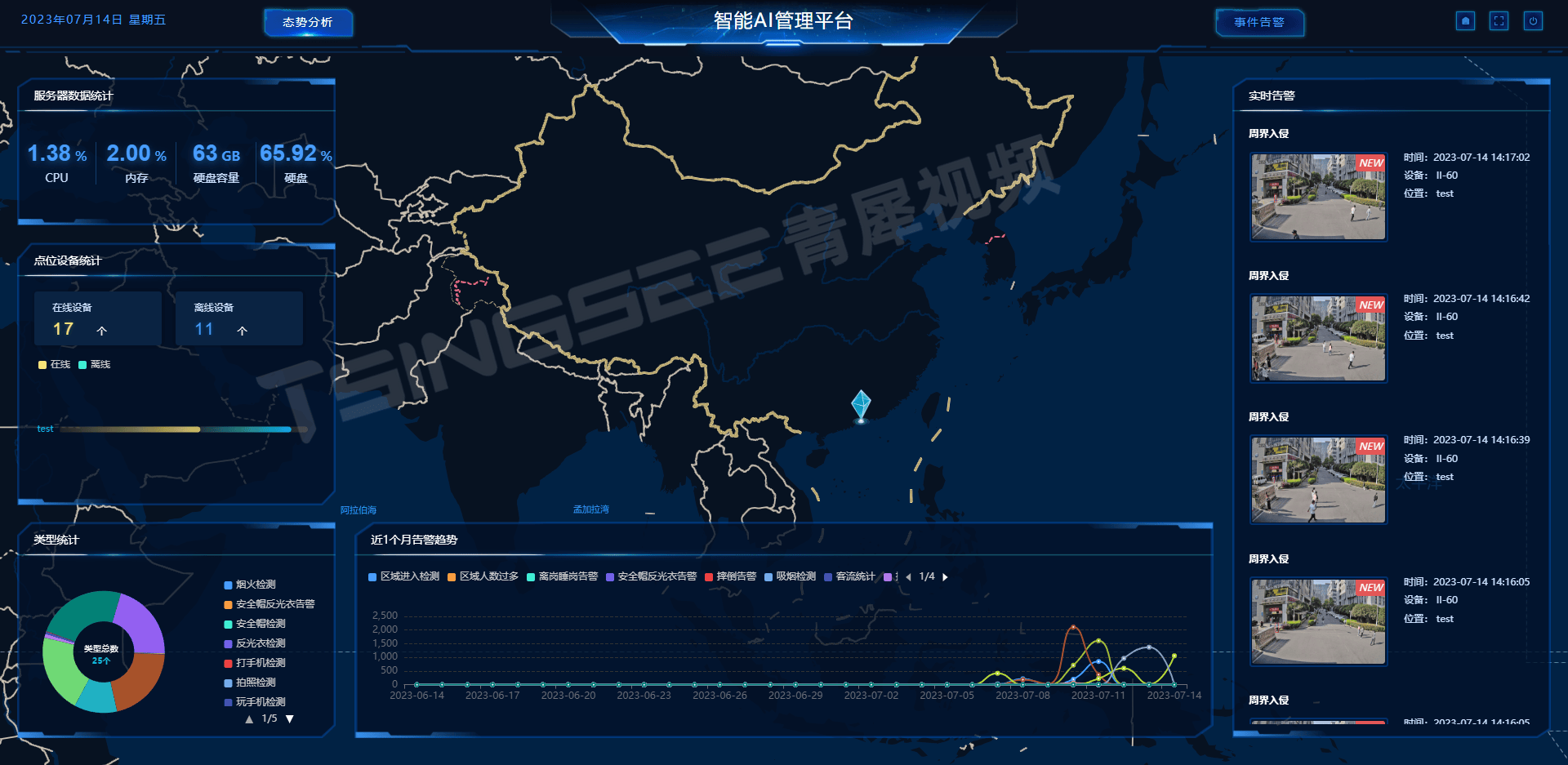
赋能未来园区:TSINGSEE视频AI智能管理平台如何引领园区管理智慧化转型
一、建设背景 随着经济的不断发展,园区产业集聚发展已成为趋势,园区逐渐成为产业聚集的重要载体。目前,国内现有的大部分园区的管理方式比较粗放、单一,范围局限于安全、环境等方面且不成体系,并且没有覆盖到应急、消…...
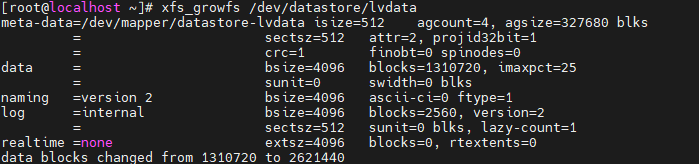
Linux逻辑卷管理LVM
系列文章目录 提示:仅用于个人学习,进行查漏补缺使用。 1.Linux介绍、目录结构、文件基本属性、Shell 2.Linux常用命令 3.Linux文件管理 4.Linux 命令安装(rpm、install) 5.Linux账号管理 6.Linux文件/目录权限管理 7.Linux磁盘管理/文件系统 提示&a…...

团队诊断工具TDS
希典梁开广老师引进的团队诊断问卷TDS(Team Diagnostic Survey)是基于卓越团队6个条件模型开发的,是用于诊断团队有效性的测评工具,其建构过程严格遵循心理测量学原理。可以帮助企业觉察团队优劣势,找到提升与发展机会,明确和强化…...

DC-5靶机渗透测试
DC-5靶场 文章目录 DC-5靶场信息收集漏洞发现漏洞利用 --- 日志文件包含漏洞利用 --- 文件包含过滤器链的RCEshell反弹权限提升 信息收集 使用--scriptvuln扫描发现了一个thankyou.php界面 感觉会有问题,前往访问网站信息 漏洞发现 来到thankyou.php界面ÿ…...

16、电科院FTU检测标准学习笔记-基本性能2
作者简介: 本人从事电力系统多年,岗位包含研发,测试,工程等,具有丰富的经验 在配电自动化验收测试以及电科院测试中,本人全程参与,积累了不少现场的经验 ———————————————————…...

MySQL——使用Python操作MySQL
文章目录 安装PyMySQL使用PyMySQL操作MySQL 在Python中操作MySQL数据库时,我们使用较多的库是 PyMySQL,如果你选择使用 PyMySQL库,那么首先需要通过pip安装它。pip install pymysql命令就是用来安装PyMySQL的。 安装PyMySQL 1.打开你的命令行工具&…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
