2024.8.12
2024.8.12 【梦最让我费解的地方在于,明明你看不清梦里人们的脸,却清晰地知道他们是谁。】
Monday 七月初九
序理论
最小链覆盖&最长反链长度
我们设定一个二元关系符R和一个集合A
我们设定<A,R>这样一个类群,那么对于任意 a i ∈ A , a j ∈ A a_i\in A,a_j \in A ai∈A,aj∈A, 二元关系式$a_i\ R\ a_j $将返还一个bool值作为结果
在此类群中,我们对二元关系符做如下规定
- 自反性(reflexive) ( ∀ a i ∈ A ) , a i R a i = t r u e (\forall a_i \in A),a_i \ R \ a_i \ = true (∀ai∈A),ai R ai =true
- 反对称性(antisymmetric) ( ∀ a , b ∈ A ) , a R b = t r u e ⇒ a = b (\forall a,b \in A),a \ R \ b \ = true \Rightarrow a\ =\ b (∀a,b∈A),a R b =true⇒a = b
- 传递性(transitive) ( ∀ a , b , c ∈ A ) , a R b = t r u e , b R c = t r u e ⇒ a R c = t r u e (\forall a,b,c\in A),a\ R \ b\ =true ,b\ R\ c\ =true \Rightarrow a\ R\ c\ = true (∀a,b,c∈A),a R b =true,b R c =true⇒a R c =true
那么对于这个类群的最小链覆盖为
B ⊂ A , ∀ x ∈ B ∃ y ∈ B ⇒ x R y = t r u e ∨ y R x = t r u e B \subset A,\forall \ x \in B \\ \exists \ y \in B\Rightarrow \\ x\ R\ y\ = true \vee y\ R\ x\ = true B⊂A,∀ x∈B∃ y∈B⇒x R y =true∨y R x =true
B为满足条件的最小集
最长反链覆盖为
B ⊂ A , ∀ x ∈ B ∀ y ∈ B ⇒ ¬ ( x R y = t r u e ∨ y R x = t r u e ) B \subset A,\forall \ x \in B \\ \forall \ y \in B\Rightarrow \\ \neg (x\ R\ y\ = true \vee y\ R\ x\ = true) B⊂A,∀ x∈B∀ y∈B⇒¬(x R y =true∨y R x =true)
B为符合条件的最大集
Dilworth 定理
对于一个这样的类集,最小链覆盖是等于最长反链覆盖的
显然,当 ∣ A ∣ < = 3 |A|<=3 ∣A∣<=3时,一定成立
我们设存在集合 C C C使得其满足该定理
使其宽度为K,若 C C C中任意元素均不可比,该定理显然成立
否则在该集合中取出一条长度大于1的链,令其中链首为 m m m,链尾为 M M M
令 T = A ∖ { m , M } T=A\setminus\{m,M\} T=A∖{m,M},若 T中的宽度不超过 d − 1 d-1 d−1,则由归纳假设知 T T T可被至多$ d-1$条链覆盖,进而 S S S 可被这些链再加上链 { m , M } \{m,M\} {m,M}覆盖,命题成立,否则说明 T T T中的宽度也为 d d d,令 T T T 中最长的一条反链为 B B B
我们考虑如下两个集合:
A + = { x ∈ A : ( ∃ a ∈ B ) a ⪯ x } A − = { x ∈ A : ( ∃ a ∈ B ) x ⪯ a } A^+=\{x\in A:(\exists a\in B) \ a \preceq x\}\\ A^-=\{x\in A:(\exists a\in B) \ x \preceq a\}\\ A+={x∈A:(∃a∈B) a⪯x}A−={x∈A:(∃a∈B) x⪯a}
我们很难不发现
A + ⊔ A − = A A + ⊓ A − = B ∣ A + ∣ < ∣ A ∣ , ∣ A − ∣ < ∣ A ∣ A^+\sqcup A^- = A\\ A^+\sqcap A^- = B\\ |A^+|<|A|,|A^-|<|A| A+⊔A−=AA+⊓A−=B∣A+∣<∣A∣,∣A−∣<∣A∣
对 S + , S − S^+,S^- S+,S−分别进行数学归纳
那么两个集合最小链覆盖数是 d d d,且均包含 B B B中一个元素
命题得证
[[ARC165E] Random Isolation]([ARC165E] Random Isolation - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
[ARC165E] Random Isolation
题面翻译
给一棵 n n n 个节点的树和一个整数 K K K。每次操作,等概率随机选一个所在连通块大小大于 K K K 的点,并删掉这个点和与之相连的所有边。重复操作直到图上所有连通块大小不超过 K K K,求期望操作次数,答案对 998244353 998244353 998244353 取模。
1 ≤ K < N ≤ 100 1\le K < N\le 100 1≤K<N≤100。
translated by yxcat.
题目描述
頂点に $ 1 $ から $ N $ の番号が付いた $ N $ 頂点からなる木があります。 $ i $ 番目の辺は頂点 $ A_i,B_i $ を結びます。
グラフの連結成分が含む頂点の数がそれぞれ $ K $ 以下になるまで以下の操作を行い続けます。
- $ N $ 個の頂点のうち、$ K+1 $ 個以上の頂点を含む連結成分に属する頂点を $ 1 $ つ一様ランダムに選ぶ。選んだ頂点を端点とする辺をすべて削除する。
操作を行う回数の期待値を $ \bmod\ 998244353 $ で求めてください。
期待値 $ \text{mod\ }{998244353} $ の定義 求める期待値は必ず有理数になることが証明できます。 また、この問題の制約のもとでは、その値を既約分数 $ \frac{P}{Q} $ で表した時、$ Q\ \not\ \equiv\ 0\ \pmod{998244353} $ となることも証明できます。 よって、$ R\ \times\ Q\ \equiv\ P\ \pmod{998244353},\ 0\ \leq\ R\ <\ 998244353 $ を満たす整数 $ R $ が一意に定まります。 この $ R $ を答えてください。
输入格式
入力は以下の形式で標準入力から与えられます。
$ N $ $ K $ $ A_1 $ $ B_1 $ $ A_2 $ $ B_2 $ $ \vdots $ $ A_{N-1} $ $ B_{N-1} $
输出格式
答えを出力してください。
样例 #1
样例输入 #1
4 2 1 2 2 3 2 4样例输出 #1
249561090样例 #2
样例输入 #2
20 10 16 8 6 2 18 3 3 12 5 1 13 9 13 19 3 11 5 13 17 6 8 14 1 16 16 20 11 15 3 10 15 4 5 18 1 7 1 17样例输出 #2
181196154提示
制約
- $ 1\ \leq\ K\ <\ N\ \leq\ 100 $
- $ 1\ \leq\ A_i,B_i\ \leq\ N $
- 与えられるグラフは木
- 入力される値はすべて整数
Sample Explanation 1
例えば $ 1 $ 回目の操作で頂点 $ 2 $ が選ばれた場合、操作によって全ての辺が削除され、操作後は各連結成分が含む頂点の数はそれぞれ $ 2 $ 以下であるため操作を終了します。一方 $ 1 $ 回目の操作で頂点 $ 1 $ が選ばれた場合、操作後頂点 $ 2,3,4 $ からなる連結成分が残るため、$ 2 $ 回目の操作が行われます。 操作回数の期待値は $ \frac{7}{4} $ です。
//2024.8.12
//by white_ice
//[ARC165E] Random Isolation | AT_arc165_e
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define int long long
#define itn long long
constexpr int oo = 105;
constexpr int mod=998244353;
int n,m;
itn siz[oo],f[oo][oo][oo],g[oo][oo];
int c[oo<<1],ic[oo<<1];
struct nod{int to[oo<<1],nxt[oo<<1],head[oo],tot;
__inline void adde(int u,int v){to[++tot]=v,nxt[tot]=head[u],head[u]=tot;}}S;
__inline int qpow(int x,int y){int ans=1;while (y){if(y&1)ans=ans*x%mod;y>>=1;x=x*x%mod;}return ans;}
__inline void dfs(int u,int fa){siz[u]=1,f[u][1][0]=1;for (int i=S.head[u];i;i=S.nxt[i]){int v=S.to[i];if (v==fa) continue;dfs(v,u);for (int j=siz[u]+siz[v];j>=0;j--)for (int k=siz[u]+siz[v];k>=0;k--)g[j][k]=f[u][j][k],f[u][j][k]=0;for (int j=siz[u];j>=1;j--)for (int k=siz[u]-j;k>=0;k--){f[u][j][k+1]=(f[u][j][k+1]+g[j][k])%mod;for (int p=siz[v];p>=1;p--)for (int q=siz[v]-p;q>=0;q--){f[u][j+p][k+q]=(f[u][j+p][k+q]+g[j][k]*f[v][p][q]%mod)%mod;} }siz[u]+=siz[v];}
}
main(void){//fre();cin.tie(0)->sync_with_stdio(0);c[0]=ic[0]=1;for (int i=1;i<=200;i++) c[i]=c[i-1]*i%mod;ic[200]=qpow(c[200],mod-2);for (int i=200-1;i>=1;i--) ic[i]=ic[i+1]*(i+1)%mod;cin >> n >> m ;for (int u,v,i=1;i<n;i++){cin >> u >> v;S.adde(u,v),S.adde(v,u);}dfs(1,0);int ans=0;for (int u=1;u<=n;u++){for (int i=m+1;i<=siz[u];i++){for (int j=0;j<=siz[u]-i;j++)ans=(ans+f[u][i][j]*c[i]%mod*c[j+(u!=1)]%mod*ic[i+j+(u!=1)]%mod)%mod;//,cout<<u<<" "<<i<<" "<<j<<" "<<f[u][i][j]<<"\n";}}cout << ans <<"\n";exit(0);
}
我们考虑,既然是计算概率,
那么对于一棵树,我们不妨将其转化为一个序列来考虑
我们假设一个序列s,我们从这个序列中选出n个点,假设已经从s中选出了x个点,那么又有n-x个点在剩余的序列中选择
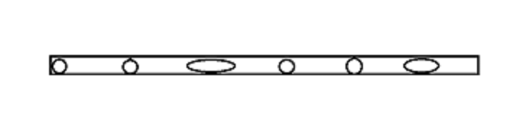
(其中椭圆为要去除的点)
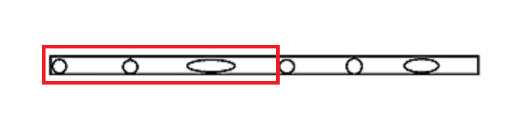
(红色部分为去除的)
那么后面的部分有n-x个点可以被选择,后半部分共k个点
那么我们将k自由组合排序,考虑第一个被选择的点
这些点的选择概率都是 1 n − x \frac{1}{n-x} n−x1,所以我们考虑组合意义,共 ( n − x ) ! ( k − n + x ) ! k ! \frac{(n-x)!(k-n+x)!}{k!} k!(n−x)!(k−n+x)!种可能
通过这种转化,我们将求解概率变为了计数问题
那么我们应该考虑如何取出点了
对于一个子树T,|T|>k,对于这个子树,我们一定可以对这一棵子树进行操作
那么我们就可以统计子树大小大于k的个数
那么他的贡献就是T出现的概率我们设T出现的概率是 p ( T ) p(T) p(T),那么答案的总期望就是 ∑ s i z e T > k p ( T ) \sum_{size_T>k}p(T) ∑sizeT>kp(T)
关于这个统计,使用树形DP求解总数即可
设 f [ x ] [ i ] [ j ] f[x][i][j] f[x][i][j]为为 x x x子树中选了包含 x x x 在内的 i i i 个点,有 j j j 个点与之相连的方案数,使用背包转移即可
[P3974 [TJOI2015] 组合数学]([P3974 TJOI2015] 组合数学 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn))
[TJOI2015] 组合数学
题目描述
为了提高智商,ZJY 开始学习组合数学。某一天她解决了这样一个问题:给一个网格图,其中某些格子有财宝。每次从左上角出发,只能往右或下走。问至少要走几次才可能把财宝全捡完。
但是她还不知足,想到了这个问题的一个变形:假设每个格子中有好多块财宝,而每一次经过一个格子至多只能捡走一块财宝,其他条件不变,至少要走几次才可能把财宝全捡完?
这次她不会做了,你能帮帮她吗?
输入格式
第一行为一个正整数 t t t,表示数据组数。
每组数据的第一行是两个正整数 n n n 和 m m m,表示这个网格图有 n n n 行 m m m 列。
接下来 n n n 行,每行 m m m 个非负整数,表示这个格子中的财宝数量( 0 0 0 表示没有财宝)。
输出格式
对于每组数据,输出一个整数,表示至少走的次数。
样例 #1
样例输入 #1
1 3 3 0 1 5 5 0 0 1 0 0样例输出 #1
10提示
数据范围
对于 30 % 30\% 30% 的数据, n ≤ 5 n \le 5 n≤5, m ≤ 5 m \le 5 m≤5,每个格子中的财宝数不超过 5 5 5 块。
对于 50 % 50\% 50% 的数据, n ≤ 100 n \le 100 n≤100, m ≤ 100 m \le 100 m≤100,每个格子中的财宝数不超过 1000 1000 1000 块。
对于 100 % 100\% 100% 的数据, 1 ≤ t ≤ 2 1\le t\le 2 1≤t≤2, 1 ≤ n ≤ 1000 1\le n \le 1000 1≤n≤1000, 1 ≤ m ≤ 1000 1\le m \le 1000 1≤m≤1000,每个格子中的财宝不超过 1 0 6 10^6 106 块。
//2024.8.12
//by white_ice
//[TJOI2015] 组合数学 | P3974
#include<bits/stdc++.h>
//#include"need.cpp"
using namespace std;
#define itn long long
#define int long long
constexpr int oo = 1003;
itn n,m;itn st[oo][oo];
int f[oo][oo];
main(void){//fre();cin.tie(0)->sync_with_stdio(0);itn t;cin >> t;
while (t--){memset(f,0,sizeof(f));cin >> n >> m;for (itn i=1;i<=n;i++)for (int j=1;j<=m;j++)cin >> st[i][j];for (itn i=1;i<=n;i++)for (itn j=m;j>=1;j--){f[i][j] = max(f[i-1][j],f[i][j+1]);f[i][j] = max(f[i-1][j+1]+st[i][j],f[i][j]);}cout << f[n][1] << '\n';
}cout << flush;exit (0);
}
我们使用,使用,使用了一段及其短小精悍的代码解决了这道题
这道题,就要使用我们上面提到的最小链覆盖&最长反链长度了
我们不难发现,对于这个网格图,在上面移动就是构造一个链的过程
从一个方格出发,可以向下或向右移动
左右我们就是要求解从第一行第一列出发,移动到最后一列最后一行的最长链长度
这是我们就可以搬出这个:Dilworth 定理
最小链覆盖 = 最长反链长度
那么我们求解最长反链长度就好啦
我们如何求解呢?对于一个格子,什么地方不能成链呢?
当然是x,y坐标一个大于该格子一个小于该格子的时候啦)
相关文章:

2024.8.12
2024.8.12 【梦最让我费解的地方在于,明明你看不清梦里人们的脸,却清晰地知道他们是谁。】 Monday 七月初九 序理论 最小链覆盖&最长反链长度 我们设定一个二元关系符R和一个集合A 我们设定<A,R>这样一个类群,那么对于任意 a i…...

使用Python解析pdf、docx等格式文件。
针对不同类型的文件,需要采取特定的访问与解析策略来有效获取其中蕴含的知识。下面我们将介绍对于不同数据源数据的获取方式。 1 解析Docx文档 1.1 获取Docx文档中文本 from docx import Document # pip install python-docx # python-docx 0.8.11 filename xx…...

Linux网络通信基础API
这篇文章只有Linux网络通信基础API大参数信息,和返回值,这篇文章并没有这些基础API的参数类型介绍。accept的第二个参数可以查看客户端信息。 创建socket #include <sys/types.h> /* See NOTES */#include <sys/socket.h>int sock…...

Python爬虫:下载4K壁纸
🎁🎁创作不易,关注作者不迷路🎀🎀 目录 🌸完整代码 🌸分析 🎁基本思路 🎁需要的库 🎁提取图片的链接和标题 👓寻找Cookie和User-Agent &…...

2024年【北京市安全员-B证】新版试题及北京市安全员-B证免费试题
题库来源:安全生产模拟考试一点通公众号小程序 2024年【北京市安全员-B证】新版试题及北京市安全员-B证免费试题,包含北京市安全员-B证新版试题答案和解析及北京市安全员-B证免费试题练习。安全生产模拟考试一点通结合国家北京市安全员-B证考试最新大纲…...

python爬取B站视频实验
实验17:爬虫2 文章目录 实验17:爬虫21.实验目标及要求2. 实验主要内容3.实验小结 1.实验目标及要求 (1)掌握有关爬虫的包 (2)掌握爬虫方法 (3)爬取B站卡塔尔世界杯若干视频 2. 实验…...

10步搞定Python爬虫从零到精通!
学习Python网络爬虫可以分为以下几个步骤,每一步都包括必要的细节和示例代码,以帮助你从零开始掌握这一技能。 第一步:理解网络爬虫基础 什么是网络爬虫? 网络爬虫是一种自动化程序,用来从互联网上收集数据.它通过发送 HTTP 请求…...

SpringMVC学习笔记---带你快速入门和复习
一、初识SpringMVC 1.1、什么是SpringMVC 1.1.1、什么是MVC MVC是一种软件架构模式(是一种软件架构设计思想,不止Java开发中用到,其它语言也需要用到),它将应用分为三块: M:Model࿰…...

Linux系统编程 day09 线程同步
Linux系统编程 day09 线程同步 1.互斥锁2.死锁3.读写锁4.条件变量(生产者消费者模型)5.信号量 1.互斥锁 互斥锁是一种同步机制,用于控制多个线程对共享资源的访问,确保在同一时间只有一个线程可以访问特定的资源或执行特定的操作…...

Vue快速入门(四)——Vue3及组合式API(一)
文章目录 一、认识Vue31. Vue2 选项式 API vs Vue3 组合式API2. Vue3的优势二、使用create-vue搭建Vue3项目1、认识create-vue2. 使用create-vue创建项目三、组合式API - setup选项1. setup选项的写法和执行时机2. setup中写代码的特点3. `<script setup>`语法糖4.小结四…...

vue项目名修改、webstorm和idea创建的项目重命名、重构项目、修改项目名称
一、需求 就是创建了一个项目,后期需要重命名,怎么办?----> 直接修改?肯定不行,因为里面有些配置也需要修改,假如你只改文件夹名称的话,里面配置都没修改,后期可能会出问题。 二…...

【MySQL】数据库约束和多表查询
目录 1.前言 2.数据库约束 2.1约束类型 2.2 NULL约束 2.3 NUIQUE:唯一约束 2.4 DEFAULT:默认值约束 2.5 PRIMARY KEY:主键约束 2.6 FOREIGN KEY:外键约束 1.7 CHECK约束 3.表的设计 3.1一对一 3.2一对多 3.3多对多 …...

抖店飞鸽客服自动回复软件开发教程与下载体验(.NET版)
转载请注明出处! 原文链接:https://blog.csdn.net/zgyulongfei/article/details/140960430 本文适合的读者为: 抖店(抖音小店)个体商家;抖店店群商家(店群商家:指的是开了几十个抖…...
如何解决,redis setnx锁的使用。)
如何关闭redis的自动清理缓存,声明式事务(含有redis)如何解决,redis setnx锁的使用。
20240809 一、解决redis数据被删除的方案1、发现问题2、解决注意!! 二、声明式事务(当有redis的时候)1. 先看代码2. Transactional(rollbackFor Exception.class)3. 如何解决redis在事务里面,如何保证原子性和一致性3…...

C#中抽象类的使用
前言 我们在C#中使用抽象类可以发挥C#多态的功能,把具有共性的方法定义在抽象类中,然后在不同的类中去实现,可增强代码的可读性、扩展性。 1、不使用抽象类 我们定义了下面两个类XiaoWang、XiaoMing,他们有一个Country方法&…...
)
揭秘网络攻击:深入理解JavaScript中的跨站点请求伪造(CSRF)
标题:揭秘网络攻击:深入理解JavaScript中的跨站点请求伪造(CSRF) 在当今数字化时代,网络安全已成为每个开发者和用户必须关注的重点。其中,跨站点请求伪造(CSRF)是一种常见的网络攻…...
【项目实战】C++视频共享点播系统
目录 一、项目介绍 1.1 对视频共享点播系统的认识 1.2服务端程序负责功能 1.3 服务端功能模块划分 1.4 项目界面演示 1.5预备知识 二.环境搭建 2.1 安装 Jsoncpp 库 2.1.1 使用jsoncpp 2.2 引入httplib库 2.2.1 安装Git(如果你的系统尚未安装Git…...

Android逆向题解 攻防世界难度4- Android2.0
Jeb打开apk 关键代码在Native函数getResult IDA 打开 so 发现代码比较简单,可以直接静态分析。 输出字符串也就是flag 长度是15,然后分成三段,第一段是可以整除3,第二段是除3取余1,第三段是除3取余等于2࿱…...

P4155 [SCOI2015] 计划
[SCOI2015] 计划 - 洛谷 核心思路 注意到, 可推出, 表示 战士 走 步到达战士位置。 若可以走到且 r < 终点 则答案 然后再加上自己这个哨兵,和走回自己的一个哨兵即可。 AC 代码 #include<bits/stdc.h> using namespace std…...
科技新闻)
今日(2024年8月12日)科技新闻
国内: 航空航天领域 我国成功发射卫星互联网高轨卫星。我国试验性冰川保护项目取得积极成效,被形容为“为冰川盖棉被”。2024西太平洋国际航次科考队起航,开启探秘深海海山之旅。我国首架固定翼海上专业搜救航空器正式列编。“祥云”as700载…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
