二叉树------最小堆,最大堆。
什么是最小堆:
堆是一种二叉树,最小堆中所有父亲节点的值都要比自己的子节点的值要小。而根节点称为堆顶。根据定义我们可以得到堆中最小元素就在堆顶。(节点左上角是编号,内部是元素值)

假设该图中的堆顶元素是24呢?显然不符合最小堆的定义,那么我们要怎么处理呢?
假设7号节点的值是1呢?显然不符合最小堆的定义,那么我们要怎么处理呢?
如何调整堆:

在该图中我们先让 24 与左孩子的值比较发现 左孩子比自己小,再看右孩子,发现右孩子比左孩子还小,于是1号节点值和3号节点值交换。然后再看3号节点的左孩子和右孩子值都比 24 小,但是6号节点值更小,所以3号节点值24和6号节点值交换,完成最小堆的向下调整。

该图我们先让7号节点与3号节点比较,发现5 比 1大 然后交换两个节点的值,3号节点再和1号节点比较发现2比1大,然后交换节点的值,完成了最小堆的向上调整。
如果忘记了怎么存储二叉树,参考这篇博文:树------二叉树-CSDN博客
具体代码:
void down(int i)//i为需要调整的节点编号。
{
int t, flag = 0;
while (2 * i <= n && flag == 0)//判断当前节点是否有左子树。
{
if (arr[i] > arr[2 * i])
t = 2 * i;
else
t = i;//如果左子树比本节点小,记录该节点下标,否则记录该节点下标。
if (2 * i + 1 <= n)//如果有右子树。
if (arr[2 * i + 1] < arr[t])
t = 2 * i + 1;//确定最终交换值的节点下标。
if (t != i)
{
swap(i, t);
i = t;
}//如果最终交换值的下标不等于本节点,证明需要交换值。
else
flag = 1;//如果没有交换,证明本节点调整完毕,退出循环。
}
}
void up(int i)//向上调整函数。
{
int flag = 0;
if (i == 1)//如果已经在堆顶,不需要调整。
return;
while (i != 1 && flag == 0)
{
if (arr[i] < arr[i / 2])
swap(i, i / 2);//如果本节点小于父亲节点,交换值,负责退出循环。
else
flag = 1;
i /= 2;//节点编号调整为父亲节点。
}
}
void swap(int i, int j)
{
int k = arr[i];
arr[i] = arr[j];
arr[j] = k;
}//交换函数。
注意点:
最大堆和最小堆差不多,最大堆定义是任何父亲节点都要比子节点要大,至于如何调整,可以改变以上代码的大小判断符号。
另外关于昨天的 Bellman-Ford算法的优化的答案博文因为某些原因今天无法更新(其实是我忘记写了。。。。。。),明天再为大家呈上。该算法博文链接如下。
图论------贝尔曼-福德(Bellman-Ford)算法-CSDN博客
相关文章:

二叉树------最小堆,最大堆。
什么是最小堆: 堆是一种二叉树,最小堆中所有父亲节点的值都要比自己的子节点的值要小。而根节点称为堆顶。根据定义我们可以得到堆中最小元素就在堆顶。(节点左上角是编号,内部是元素值) 假设该图中的堆顶元素是24呢&a…...

预约功能的知识整理
前置知识 如果项目为小程序的开发项目中: 我们确定数据库中有的字段有: 预约人姓名、手机号、家人名称、预约时间 根据我们的经定一表必须要有的6个字段: 主键、创建时间、修改时间、创建人、修改人、备注 使用我们现在有的字段为: 主键…...

Linux的常用操作-02
一:Linux的系统目录结构 /bin bin是ary的缩写,这个目录存放着最经常用的命令 /boot:这里存放的是启动Linux时使用的一些核心文件,包括一些连接文件以及镜像文件。 /dev:dev是Device(设备)的缩写,该目录下存放的是Lin…...

Android Studio 连接手机进行调试
总所周知,Android Studio里的虚拟手机下载后又大又难用。不如直接连手机用。本篇文章主要内容为Android Studio怎么连接手机进行程序调试。 1. 在AndroidSDK中下载google USB Driver: 2. 连接手机: 进入电脑设备管理器界面。并点开便携设备,…...

Vue3项目创建及相关配置
Vue是一种用于构建用户界面的JavaScript框架。它采用了一种称为MVVM(Model-View-ViewModel)的架构模式。 MVVM是一种将用户界面与业务逻辑和数据分离的设计模式。它包括三个部分: Model(模型):表示应用程序…...

【Python】Python中一些有趣的用法
Python是一种非常灵活和强大的编程语言,它有很多有趣的用法,以下是一些例子: 一行代码实现FizzBuzz: print(\n.join([FizzBuzz[i%3*4:i%5*8:-1] or str(i) for i in range(1, 101)]))使用列表推导式生成斐波那契数列: …...

RCE复现问题和研究
目录 先了解一些常见的知识点 PHP常见命令执行函数 call_user_func eval() call_user_func_array array_filter 实战演练(RCE)PHP Eval函数参数限制在16个字符的情况下 ,如何拿到Webshell? 1、长度…...

MySQL中的索引——适合创建索引的情况
1.适合创建索引的情况 1、字段的数值有唯一性的限制 2、频繁作为 WHERE 查询条件的字段 某个字段在 SELECT 语句的 WHERE 条件中经常被使用到,那么就需要给这个字段创建索引了。尤其是在数据量大的情况下,创建普通索引就可以大幅提升数据查询的效率。 …...

5款在线伪原创改写软件,智能改写文章效果好
在这个信息爆炸的时代,内容创作变得愈发重要,而对于创作者来说,有时需要一些得力的伪原创改写工具来辅助我们更好地改写出高质量的内容。今天我要和大家分享5款令人惊喜的在线伪原创改写软件,它们以出色的智能改写效果,…...

opencv-python图像增强四:多曝光融合(方法一)
文章目录 一、简介:二、多曝光融合方案:三、算法实现步骤3.1 读取图像与曝光时间:3.2 计算响应曲线并合并3.3 色调映射 四:整体代码实现五:效果 一、简介: 在摄影和计算机视觉领域,高动态范围&…...

Qt 实战(9)窗体 | 9.2、QDialog
文章目录 一、QDialog1、基本概念2、常用特性2.1、模态与非模态2.2、数据交互 3、总结 前言: Qt框架中的QDialog类是一个功能强大且灵活的对话框控件,广泛应用于各种GUI(图形用户界面)应用程序中,用于处理用户输入、消…...

Spring 事务机制
1. 引言 1.1 什么是事务 事务是由用户定义的一系列操作序列所组成的最小工作单元;这些操作要么全部完成,要么全部不完成,是一个不可分割的工作单元。常见于数据库中的并发控制和数据一致性处理场景。 1.2 事务的特性 事务具有以下特性&am…...

Android 13 GMS 内置壁纸
如图,原生系统上,设备上的壁纸 显示系统内置壁纸。如果没有添加内置壁纸,就显示默认的壁纸。点击进去就是预览页面 扩展下,默认壁纸在 frameworks/base/core/res/res/drawable-sw720dp-nodpi/default_wallpaper.png frameworks/b…...

【LeetCode】234. 回文链表
回文链表 题目描述: 给你一个单链表的头节点 head ,请你判断该链表是否为回文链表。如果是,返回 true ;否则,返回 false 。 示例 1: 输入:head [1,2,2,1] 输出:true示例 2&#…...

零基础学会机器学习,到底要多久?
这两天啊,有不少朋友和我说,想学机器学习,但是之前没有基础,不知道能不能学得会。 首先说结论,只要坚持,就能学会,但是一定不能三天打鱼两天晒网,要持之以恒,至少每隔两…...
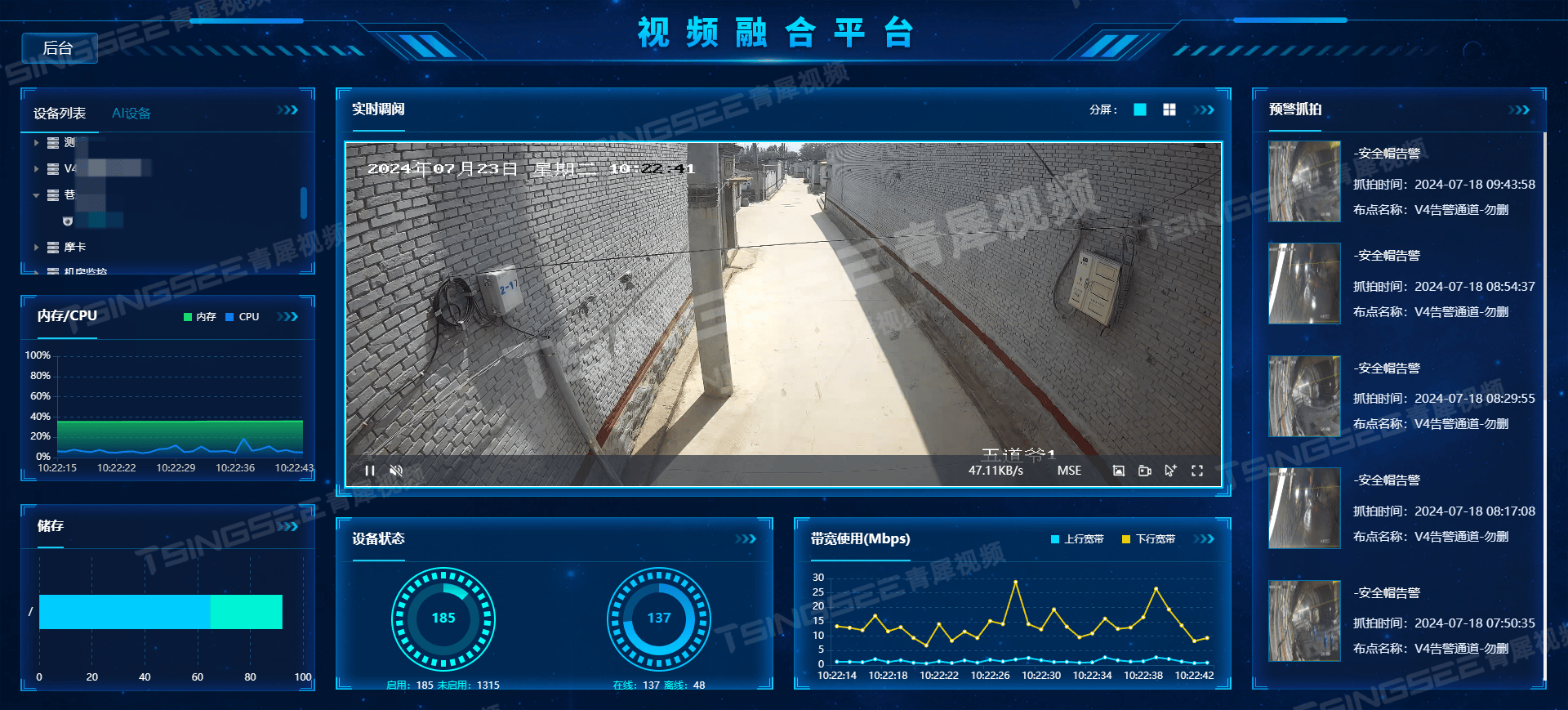
视频汇聚/安防监控综合平台EasyCVR接入海康私有协议EHOME显示失败是什么原因?
安防监控/视频综合管理平台/视频集中存储/磁盘阵列EasyCVR视频汇聚平台,支持多种视频格式和编码方式(H.264/H.265),能够轻松对接各类前端监控设备,实现视频流的统一接入与集中管理。安防监控EasyCVR平台支持多种流媒体…...

Qt解析XML
背景 本来想解析VS的项目配置文件(*.vcxproj),配合cppclean来发现多余的#incldue。 结果发现低估了难度,VS会间接引入许多目录。 略有不甘,暂且作为一个解析XML文件的示例。 代码 VSProjectParser.h #include <QVector> #include…...

PwnLab: init-文件包含、shell反弹、提权--靶机渗透思路讲解
Vulnhub靶机链接回【PwnLab】 首页有一个登录框 image-20240807124822770 他没有验证码,我们试试暴力破解 image-20240807122743025 开始爆破了,全部失败,哈哈哈 image-20240807122851001 nmap全端口扫描试试 image-20240807131408315 有…...

OpenCV—二值化Threshold()、adaptiveThreshold()
cv2.threshold() c:double cv::threshold ( InputArray src, OutputArray dst, double thresh, double maxval, int type ) (注:源图片, 目标图, 阈值, 填充色, 阈值类型) python:cv.threshold(src,thresh, maxval, type[, dst]) src:源图片…...
)
第二天:java面向对象编程(OOP)
第二天:java面向对象编程(OOP) 1. 深入理解OOP四大特性 封装(Encapsulation):学习如何将数据(属性)和操作数据的方法(行为)组合成一个独立的单元࿰…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
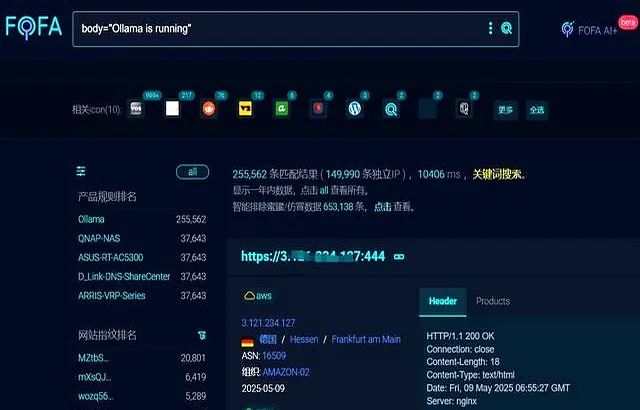
未授权访问事件频发,我们应当如何应对?
在当下,数据已成为企业和组织的核心资产,是推动业务发展、决策制定以及创新的关键驱动力。然而,未授权访问这一隐匿的安全威胁,正如同高悬的达摩克利斯之剑,时刻威胁着数据的安全,一旦触发,便可…...

深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀”
深入浅出JavaScript中的ArrayBuffer:二进制数据的“瑞士军刀” 在JavaScript中,我们经常需要处理文本、数组、对象等数据类型。但当我们需要处理文件上传、图像处理、网络通信等场景时,单纯依赖字符串或数组就显得力不从心了。这时ÿ…...

Ubuntu 安装 Mysql 数据库
首先更新apt-get工具,执行命令如下: apt-get upgrade安装Mysql,执行如下命令: apt-get install mysql-server 开启Mysql 服务,执行命令如下: service mysql start并确认是否成功开启mysql,执行命令如下&am…...
