图论------迪杰斯特拉(Dijkstra)算法求单源最短路径。
编程要求
在图的应用中,有一个很重要的需求:我们需要知道从某一个点开始,到其他所有点的最短路径。这其中,Dijkstra 算法是典型的最短路径算法。
本关的编程任务是补全右侧代码片段中 Begin 至 End 中间的代码,实现 Dijkstra 算法求单源最短路径,具体要求如下:
补全代码 int[] Paths(int source) 方法,实现 Dijkstra 算法;
输出源点 source 到其他各个定点的距离,如果不可达,则距离输出 INF。
测试举例
测试过程:
平台将创建用户补全后的ShortestPath类的对象;
调用对象的addEdge(int u, int v, int w)方法,添加边和边的权重信息,构建图G;
调用对象的Paths(int source)方法执行Dijkstra算法,求最短路径,并输出返回的最短路径,这里源点设置为1;
接着根据程序的输出判断程序是否正确。
以下是测试样例:
测试输入:
5 7
1 2 8
1 3 1
1 4 2
3 4 2
2 4 3
3 5 3
4 5 3
(5 和 7 分别表示顶点数和边数)
预期输出:
0 5 1 2 4
思路解析:
求单源最短路径就是求一个点到除它以外所有点的最短距离,首先我们还是用邻接矩阵来储存图的信息。以测试输入为例,示意图如下。

既然是求1的单源最短路径,那我们就定义一个数组dic[n+1],将dic初始化存储从1到所有点的直接距离。比如dic[1]到dic[5]分别是【0,8,1,2,99999999】,因为1无法直接到5,所以初始化为99999999。
然后找出dic里面1到2-n之间的最短距离,发现是dic[3] = 1,然后找1通过3能到达的地方,发现能到达4和5,如果1通过3到达4的话,得出dic[4] = 2 < dic[3]+arr[3][4] = 3,无法使到四的路程更短,所以不改变dic[4]的值,但是我们发现到达5,即dic[5] = 99999999>dic[3]+arr[3][5] = 4,能使1到5距离缩短,于是改变dic[5]的值。这样我们就得到能通过3进行优化一轮路径,学术名叫做松弛。

我们知道,如果已经通过3实现了一轮优化,那么我们将进一步缩短路程的话,是不能走回头路的,因为如果再次经过3的话没有意义,所以最短路没有重复路径。
那么我们就要定义一个数组来存储已经作为转点进行一轮松弛的点,我们可以定义book[n+1]来存储。将作为转点的点比如3,用book[3] = 1,表示已经使用过。
之后便是重复步骤,找除去dic[3]以外的最小值,也就是dic[4],继续进行一轮松弛,将4这个点用book[4] = 1,表示已经使用过。
之后的图大家可以自己试着来画出。
具体代码:
#include<stdio.h>
int main(void)
{
int arr[100][100] = { 0 };
int dic[100];
int book[100] = { 0 };
int m, n, a, b, c, u, v;
int inf = 99999999;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (i == j)
arr[i][j] = 0;
else
arr[i][j] = inf;
for (int i = 1; i <= m; i++)
{
scanf("%d%d%d", &a, &b, &c);
arr[a][b] = c;
arr[b][a] = c;
}//无向图初始化。
for (int i = 1; i <= n; i++)
dic[i] = arr[1][i];//初始化dic数组
for (int i = 1; i <= n - 1; i++)//最多要进行n-1轮松弛,i值不会使用,仅仅表示循环多少轮。
{
int min = inf;
for (int j = 2; j <= n; j++)
{
if (book[j] == 0 && dic[j] < min)
{
min = dic[j];
u = j;
}
}//找出从1到任意数字的最短值。
book[u] = 1;//将该位置提前存储,表示已经使用过。
for (v = 2; v <= n; v++)//优化1通过u到所有点的路径。
{
if (arr[u][v] < inf)//如果u到v没有通路,也就没办法优化。
{
if (dic[v] > dic[u] + arr[u][v])
dic[v] = dic[u] + arr[u][v];//优化赋值过程。
}
}
}
for (int i = 1; i <= n; i++)
printf("%d ", dic[i]);//打印结果。
return 0;
}
注意:
实际上迪杰斯特拉算法可以看作是贪心算法,通过每一步的最优解组合成全局最优解,感兴趣的同学们可以去网上查找关于贪心算法的知识,这种类型的题目我们以后也会分享。
相关文章:

图论------迪杰斯特拉(Dijkstra)算法求单源最短路径。
编程要求 在图的应用中,有一个很重要的需求:我们需要知道从某一个点开始,到其他所有点的最短路径。这其中,Dijkstra 算法是典型的最短路径算法。 本关的编程任务是补全右侧代码片段中 Begin 至 End 中间的代码,实现 …...
题解)
河工院首届工业设计大赛程序组(挑战赛)题解
更好的阅读体验 \huge{\color{red}{更好的阅读体验}} 更好的阅读体验 寻找ACMer 思想: 签到题按照题意遍历字符串,不断向后寻找包含 ACMer 完整字符串的数量即可 std标程: #include <iostream> #include <cstring> #include …...

文件上传漏洞(二,靶场搭建及漏洞利用)
前言: 本文基于github上的upload-labs,PHP study以及bp抓包软件进行操作。 一,靶场搭建。 靶场链接 1,下载zip文件到PHP study下的www文件夹内,并解压。 2,创建网站。 此处php版本应选择较老版本&…...

大厂面试题分享第二期
大厂面试题分享第二期 如果执行了一条命令,"select count(*)from…",使用哪个引擎更快,为什么?垃圾回收器 CMS 和 G1的区别介绍一下CMS和G1CMS(并发)垃圾收集器G1垃圾回收器 HTTPS和HTTP的区别主…...

zabbix安装
a.安装 Zabbix 仓库 # rpm -Uvh https://repo.zabbix.com/zabbix/5.0/rhel/7/x86_64/zabbix-release-5.0-1.el7.noarch.rpm # yum clean all b. 安装 Zabbix server、前端、agent # yum install zabbix-server-mysql zabbix-agent c. 安装Zabbix前端 启用红帽软件集合 # …...

SpringBoot集成日志框架
SpringBoot集成日志框架 Java生态体系日志框架介绍 简介 在Java生态体系中,围绕着日志,有很多成熟的解决方案。关于日志输出,主要有两类工具。 一类是日志框架(Log4j、Logback),主要用来进行日志的输出的…...

CSS笔记总结(Xmind格式):第三天
Xmind鸟瞰图: 简单文字总结: css知识: 边框线: 1.border-width:边框的粗细 2.border-style:边框线的样式(solid实线,double双实线,dotted点线,dashed虚线) 3.border-color:边框线的颜色 4.简写形式&a…...

WordPress原创插件:Keyword-ranking-seo 1.0 关键词排名插件 有利于seo
WordPress原创插件:Keyword-ranking-seo 1.0 关键词排名插件 有利于seo 当用户访问网站时,该链接会随机选择一个关键词,并使用选定的搜索引擎进行搜索。 插件下载链接 https://download.csdn.net/download/huayula/89632792...

Docker Swarm 管理
Docker Swarm 是 Docker 提供的一种用于管理容器集群的工具。一、Docker Swarm 的主要特点包括: 高可用性:可以自动检测和恢复故障节点,确保服务的持续可用性。 例如,当某个工作节点出现故障时,Swarm 会将其上的任务重…...

跨平台、多格式、云同步,Koodo Reader背后的技术亮点
前言 对于像我这样的书虫来说,能够找到一个既方便又舒适的阅读环境,简直就是人生中的一大幸事;今天,就让小江湖我带你走进一个不一样的阅读世界——Koodo Reade! 无论是在喧嚣的都市,还是在宁静的乡村&a…...

【Story】如何高效记录并整理编程学习笔记?
目录 一、为何笔记在编程学习中如此重要?1.1 知识的捕捉1.2 理解和消化1.3 知识的复习1.4 知识的分享 二、建立高效的笔记系统2.1 确定笔记的目标2.2 选择合适的工具2.3 笔记的结构化2.4 记录有效的内容2.5 定期回顾和更新 三、保持笔记条理性的技巧3.1 使用一致的格…...
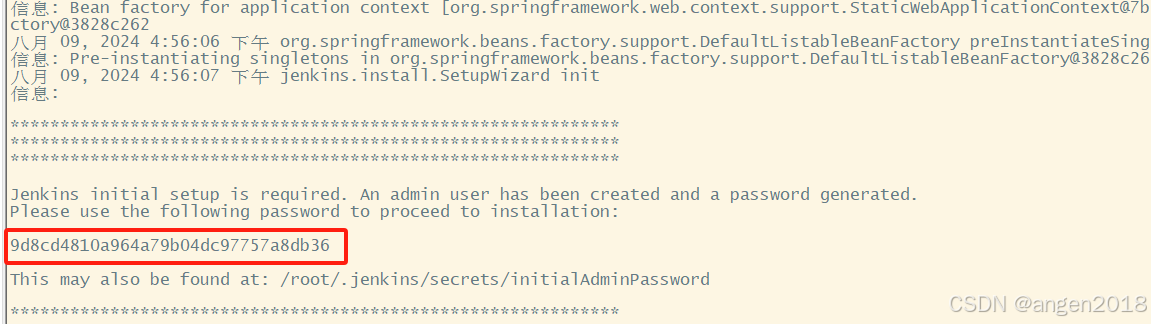
jenkins 安装以及自动构建maven项目并且运行
在这里找到你对应jdk的版本的jenkins包 War Jenkins Packages 我这里用的使java8,所以下载 https://mirrors.jenkins.io/war-stable/2.60.1/jenkins.war 然后jenkins可以安装到centos系统 在本地windows系统运行命令行 scp C:\Users\98090\Downloads\jenkins.war root@192…...

Java虚拟机:虚拟机介绍
大家好,我是栗筝i,这篇文章是我的 “栗筝i 的 Java 技术栈” 专栏的第 033 篇文章,在 “栗筝i 的 Java 技术栈” 这个专栏中我会持续为大家更新 Java 技术相关全套技术栈内容。专栏的主要目标是已经有一定 Java 开发经验,并希望进…...
硬件面试经典 100 题(31~40 题)CRE4
31、多级放大电路的级间耦合方式有哪几种?哪种耦合方式的电路零点偏移最严重?哪种耦合方式可以实现阻抗变换? 有三种耦合方式:直接耦合、阻容耦合、变压器耦合。直接耦合的电路零点漂移最严重,变压器耦合的电路可以实现…...

ReactNative笔记(自用)
环境 ios更换gem镜像源: 查看当前源: gem sources -l 移除默认源: gem sources --remove https://rubygems.org/。添加新的源: 添加 Ruby China 的镜像源: gem source -a https://gems.ruby-china.com/或者添加其他镜像源。 清华大学的gem源: htt…...
)
嵌入式八股-面试30题(20240812)
TCP和UDP的区别是什么? **TCP(Transmission Control Protocol)**是面向连接的协议,提供可靠的、顺序的数据传输。它通过三次握手建立连接,并在数据传输过程中使用确认和重传机制来确保数据的正确性。TCP还支持流量控制和拥塞控制…...
)
单一职责原则(SRP)
目录 1、定义 2、优点 3、原则的重要性 4、 示例 5、注意事项 单一职责原则(Single Responsibility Principle, SRP)是面向对象设计中的一项重要原则,属于 SOLID 原则之一。它的核心思想是:一个类应该只有一个引起它变化的原因&am…...

骨传导耳机怎么选?分享五款资深用户都说好的骨传导耳机!
在追求健康生活的道路上,运动健身已成为一种时尚潮流,而音乐则是这场潮流中不可或缺的催化剂。然而,传统耳机在运动场景下的局限性日益凸显,难以满足运动者对自由与舒适的双重追求。正是基于这样的市场需求,骨传导耳机…...

【计算机网络——分组延时,丢失,吞吐量】
处理延时:1检查分组首部信息,决定将该分组导向何处所需时间。2检查比特级别的差错所需时间:分析这个分组是否出错,目标IP地址字段提取出来,查路由表……。 传播延时和传输延时:传输延时就是分组到链路所需…...

使用1panel 申请证书配置雷池站点
1.创建测试站点 2.使用1panel申请测试站点的自签名证书 ps:雷池支持自签的证书 关于如果选择网站的SSL证书 百度搜索 看起来是证书的问题 调整了参数重新申请一个证书上传 注意,如果文件上传错了,雷池会报错,如下图 再次访问配…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
