【学习笔记】用线段树维护区间计数问题
前言
简单的区间计数问题可能直接推式子就行了。
但有些问题必须要数据结构维护。线段树就是一个比较好的处理区间的数据结构。
Gym102222L


思路
满足条件的区间特征: max { a i } − min { a i } + 1 − c n t = 0 \max\{a_i\}-\min\{a_i\}+1-cnt=0 max{ai}−min{ai}+1−cnt=0,其中 c n t cnt cnt 代表区间内不同数字的个数。
考虑固定右端点,统计有多少个合法的左端点。
我们可以用线段树维护 m i n v = min { max { a i } − min { a i } − c n t } minv=\min\{\max\{a_i\}-\min\{a_i\}-cnt\} minv=min{max{ai}−min{ai}−cnt} 和 n u m = 有多少个区间左端点可以取到 m i n v num=有多少个区间左端点可以取到 minv num=有多少个区间左端点可以取到minv,答案就是 m i n v = − 1 minv=-1 minv=−1 时的 n u m num num
max { a i } \max\{a_i\} max{ai} 和 min { a i } \min\{a_i\} min{ai} 可以用两个单调栈维护。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+7,inf=1e18;
struct seg
{int minv,tag,cnt;seg(){minv=tag=cnt=0;}
};
vector<seg> tr;
void update(int u)
{tr[u].minv=min(tr[u<<1].minv,tr[u<<1|1].minv);if(tr[u<<1].minv==tr[u<<1|1].minv){tr[u].cnt=tr[u<<1].cnt+tr[u<<1|1].cnt;}else if(tr[u].minv==tr[u<<1].minv){tr[u].cnt=tr[u<<1].cnt;}else if(tr[u].minv==tr[u<<1|1].minv){tr[u].cnt=tr[u<<1|1].cnt;}else{assert(false);}
}
void pushdown(int u)
{if(tr[u].tag){tr[u<<1].minv+=tr[u].tag; tr[u<<1|1].minv+=tr[u].tag;tr[u<<1].tag+=tr[u].tag; tr[u<<1|1].tag+=tr[u].tag;tr[u].tag=0;}
}
void build(int u,int st,int ed)
{if(st==ed){tr[u].cnt=1;return;}int mid=st+ed>>1;build(u<<1,st,mid);build(u<<1|1,mid+1,ed);update(u);
}
void modify(int u,int st,int ed,int l,int r,int x)
{if(l<=st&&ed<=r){tr[u].minv+=x;tr[u].tag+=x;return;}pushdown(u);int mid=st+ed>>1;if(mid>=l)modify(u<<1,st,mid,l,r,x);if(mid<r)modify(u<<1|1,mid+1,ed,l,r,x);update(u);
}
int query(int u,int st,int ed,int l,int r)
{if(l<=st&&ed<=r){return tr[u].minv==-1?tr[u].cnt:0;}pushdown(u);int mid=st+ed>>1;int res=0;if(mid>=l)res=query(u<<1,st,mid,l,r);if(mid<r)res+=query(u<<1|1,mid+1,ed,l,r);return res;
}
int O_o()
{int n;cin>>n;tr.assign(n+1<<2,seg());vector<int> a(n+1),ls(n+1);map<int,int> mp;for(int i=1; i<=n; i++){cin>>a[i];ls[i]=mp[a[i]];mp[a[i]]=i;}build(1,1,n);stack<array<int,2>> sx,sy;// decrease, increaseint ans=0;for(int i=1; i<=n; i++){int x=a[i];while(sx.size()&&x>sx.top()[0]){auto [v,id]=sx.top(); sx.pop();modify(1,1,n,sx.size()?(sx.top()[1]+1):1,id,x-v);}sx.push({x,i});while(sy.size()&&x<sy.top()[0]){auto [v,id]=sy.top(); sy.pop();modify(1,1,n,sy.size()?(sy.top()[1]+1):1,id,v-x);}sy.push({x,i});modify(1,1,n,ls[i]+1,i,-1);ans+=query(1,1,n,1,i);}return ans;
}
signed main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cout<<fixed<<setprecision(12);int T=1;cin>>T;for(int i=1; i<=T; i++){cout<<"Case #"<<i<<": "<<O_o()<<"\n";}
}
2024牛客暑期多校训练营7 D


思路
首先预处理每个点要往后走到哪才会出现 k k k 次和 k + 1 k+1 k+1 次
具体的,令 L i L_i Li 为从点 i i i 往后走,出现 k k k 次 a i a_i ai 的最近位置;令 R i R_i Ri 为从点 i i i 往后走,出现 k k k 次 a i a_i ai 的最远位置。
考虑倒着枚举左端点,对于每个左端点考虑有多少个右端点是合法的。
我们定义点 i i i 的合法区间为 [ L i , R i ] ∪ [ 1 , i − 1 ] [L_i,R_i]∪[1,i-1] [Li,Ri]∪[1,i−1] ( [ L i , R i ] [L_i,R_i] [Li,Ri] 中 a i a_i ai 出现了 k k k 次, [ 1 , i − 1 ] [1,i-1] [1,i−1] 不在 i i i 的管辖范围内),那么对于 i i i 为左端点的答案就是 [ i , n ] [i,n] [i,n] 中所有不同的数最前面的合法区间的交集。
也就是我们要维护一棵线段树,支持区间加、区间减、求区间最大值和最大值个数。这样做其实有些麻烦。
不难想到,合法区间的交集 = 不合法区间的并集的反集,求区间的并就完全可以像扫描线那样做。
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+7,inf=1e18;
struct seg
{int val,len;seg(){val=len=0;}
};
vector<seg> tr;
int n;
void update(int u,int st,int ed)
{if(tr[u].val>0){tr[u].len=ed-st+1;}else{if(st==ed){tr[u].len=0;return;}tr[u].len=tr[u<<1].len+tr[u<<1|1].len;}
}
void add(int u,int st,int ed,int l,int r,int x)
{if(l>r||l>n||r>n) return;if(l<=st&&ed<=r){tr[u].val+=x;update(u,st,ed);return;}
// pushdown(u);int mid=st+ed>>1;if(mid>=l)add(u<<1,st,mid,l,r,x);if(mid<r)add(u<<1|1,mid+1,ed,l,r,x);update(u,st,ed);
}
int query(int u,int st,int ed,int l,int r)
{if(l>r||l>n||r>n) return 0;if(l<=st&&ed<=r){return tr[u].len;}int mid=st+ed>>1;int res=0;if(mid>=l)res=query(u<<1,st,mid,l,r);if(mid<r)res+=query(u<<1|1,mid+1,ed,l,r);return res;
}
void O_o()
{int k;cin>>n>>k;map<int,vector<int>> mp;vector<int> a(n+1);for(int i=1; i<=n; i++){cin>>a[i];mp[a[i]].push_back(i);}tr.assign((n<<2)+1,seg());vector<array<int,2>> pos(n+1);vector<int> p,nxt(n+1);p.push_back(-1);for(auto [v,t]:mp){p.push_back(v);int m=t.size();for(int i=0; i<m; i++){int l,r;if(i+k-1>=m){l=n+1;}else l=t[i+k-1];if(i+k>=m){r=n+1;}else r=t[i+k];pos[t[i]]={l,r};if(i==m-1)nxt[t[i]]=n+1;else nxt[t[i]]=t[i+1];}}int ans=0;for(int i=n; i>=1; i--){if(nxt[i]!=n+1){auto [l,r]=pos[nxt[i]];add(1,1,n,nxt[i],l-1,-1);add(1,1,n,r,n,-1);}auto [l,r]=pos[i];add(1,1,n,i,l-1,1);add(1,1,n,r,n,1);int t=query(1,1,n,i,n);ans+=(n-i+1)-t;}cout<<ans<<"\n";
}
signed main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);cout<<fixed<<setprecision(12);int T=1;cin>>T;while(T--){O_o();}
}
相关文章:

【学习笔记】用线段树维护区间计数问题
前言 简单的区间计数问题可能直接推式子就行了。 但有些问题必须要数据结构维护。线段树就是一个比较好的处理区间的数据结构。 Gym102222L 思路 满足条件的区间特征: max { a i } − min { a i } 1 − c n t 0 \max\{a_i\}-\min\{a_i\}1-cnt0 max{ai}…...

4章11节:用R做数据重塑,数据的特征缩放和特征可视化
由于数据往往复杂多样,其中不同的特征变量可能具有不同的数值范围,这使得特征缩放成为一个必要的步骤。例如,当我们要处理医学数据时,对于同一个患者,肺活量的变化范围可能在1000到5000之间,而体重指数(BMI)的变化范围则可能在10到50之间,其他一些生理指标甚至可能处于…...

LVS-NAT + LVS-DR
LVS 现在lvs已经是linux内核标准的一部分,使用lvs可以达到的技术目标是:通过linux达到负载均衡技术和linux操作系统实现一个高性能高可用的linux服务器集群,他具有良好的可靠性,可延展性和可操作性,从而以低廉的成本实…...

排序算法——插入排序
一、插入排序概念 直接插入排序(Insertion Sort)是一种简单的排序算法,它的工作原理类似于人们手动排序卡片的方式。该算法通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插…...

重修设计模式-行为型-状态模式
重修设计模式-行为型-状态模式 先了解一下状态机的概念,状态机是软件编程中对一种状态场景的抽象表达,构成状态机三要素是:状态(State)、事件(Event)、动作(Action)&…...

网络安全知识渗透测试
渗透测试是一种模拟网络攻击,用于识别漏洞并制定规避防御措施的策略。及早发现缺陷使安全团队能够修复任何漏洞,从而防止数据泄露,否则可能会造成数十亿美元的损失。笔测试还有助于评估组织的合规性、提高员工对安全协议的认识、评估事件响应…...

我国卫星互联网产业集群崛起;1000万资金扶持 上海助推产业互联网平台跨越式发展;河南“数据要素×”行动实施方案发布 | 产业互联网观察第179期
我国卫星互联网产业集群崛起:千帆星座首批卫星发射成功 8月6日,中国版"星链"项目"千帆星座"(G60星链)首批18颗组网卫星在太原卫星发射中心成功发射升空。这些卫星采用上海格思航天自主研发的可堆叠型平板卫星…...

《RT-DETR》论文笔记
原文出处 [2304.08069] DETRs Beat YOLOs on Real-time Object Detection (arxiv.org)https://arxiv.org/abs/2304.08069 原文笔记 What DETRs Beat YOLOs on Real-time Object Detection 1、设计了一种高效的混合编码器,通过解耦尺度内交互和跨尺度融合来提高…...

输出Docker容器的启动命令行脚本
当Docker容器启动后,如果忘记启动参数,比如目录挂载、端口映射等,可以通过Portainer等容器管理工具查看。但是,有时希望能获取容器启动的命令行,因为需要再启动一个类似容器,怎么办呢? 有一款工…...

Dubbo 快速掌握 这篇就够了
1. Dubbo概述 Dubbo 是一款高性能、轻量级的开源Java RPC框架,由阿里巴巴公司开发并在2011年开源。它主要用于解决分布式系统中服务之间的通信问题,支持多种协议,如Dubbo、HTTP、Hessian等,具有服务注册、服务发现、负载均衡、故…...

【每日刷题】Day100
【每日刷题】Day100 🥕个人主页:开敲🍉 🔥所属专栏:每日刷题🍍 🌼文章目录🌼 1. 【模板】堆_牛客题霸_牛客网 (nowcoder.com) 2. 【模板】链表_牛客题霸_牛客网 (nowcoder.com) 3…...

网络协议九 应用层 HTTPS
一 什么是 HTTPS 二 什么是 SSL/TLS 协议 ,TLS 是 SSL 升级后的名字 三. TLS 协议 工作在那一层 四 。OpenSSL 是 SSL/TLS协议的开源实现。 五。重点 HTTPS 的通讯过程 六 TLS 1.2 的连接过程 1. client hello 是浏览器发送给服务器的第一条信息, 是客户…...

【ArrayList】JDK1.8源码详细注释 以及如何实现线程安全的链表
ArrayList(JDK8) ArrayList有四个内部类,成员内部类Itr,成员内部类ListItr,静态内部类SubList,ArrayListSpliterator(暂时用不到)Itr是Iterator的实现类,支持正向遍历,ArrayList的i…...

[python]rasterio运行代码警告proj_create_from_database: Cannot find proj.db
这个报错要分原因还有rasterio版本讨论,因此官方给出了十分具体回答 Frequently Asked Questions What does "RasterioIOError: file.ecw not recognized as a supported file format." mean? This exception is raised when none of rasterios format …...

ThinkPHP5.1.C+CmsEasy-SQL注入
目录 1、ThinkPHP 中存在的 SQL注入 漏洞( select 方法注入) 1.1环境配置 1.1.1将 composer.json 文件的 require 字段设置成如下: 1.1.2设置application/index/controller/Index.php 文件 1.1.3在 application/database.php 文件中配置…...

Python 绘图进阶之词云图:文本数据的可视化艺术
Python 绘图进阶之词云图:文本数据的可视化艺术 引言 在数据科学和自然语言处理领域,词云图(Word Cloud)是一种常用的可视化工具。它通过直观的图形展示文本数据中的高频词汇,使得我们能够快速抓住文本内容的核心主题…...
【Windows】Q-Dir(资源管理器)软件介绍
软件介绍 Q-Dir是一款免费的文件管理器软件,它可以让您更方便地浏览和管理计算机上的文件和文件夹。与Windows自带的资源管理器相比,Q-Dir具有更多的功能和选项。 安装教程 软件下载完成,解压软件。 点击Q-Dir.exe即可打开软件。 功能…...
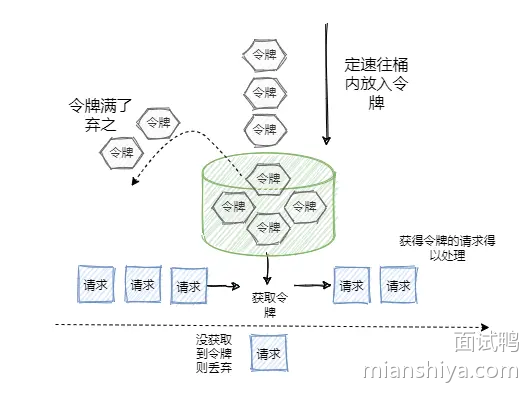
什么是令牌桶算法?工作原理是什么?使用它有哪些优点和注意事项?
大家好,我是鸭鸭! 此答案节选自鸭鸭最近弄的面试刷题神器面试鸭 ,更多大厂常问面试题,可以点击下面的小程序进行阅读哈! 目前这个面试刷题小程序刚出,有网页和小程序双端可以使用! 回归面试题…...

C++-类与对象(中上篇)
一、目标 1. 类的 6 个默认成员函数 2. 构造函数 3. 析构函数 二、对目标的介绍 1. 类的6个默认成员函数 如果一个类中什么成员都没有,简称为空类。 空类中真的什么都没有吗?并不是,任何类在什么都不写时,编译器会自动生…...

链表 206.反转链表
一般方法 不需要一个个来回换,只需要改变链表的指向,即可完成 一个链表的头节点,也代表了整个链表 class Solution {public ListNode reverseList(ListNode head) {ListNode temp;ListNode cur head;ListNode pre null;while(cur ! null…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
