LCA(Lowest Common Ancestor)
LCA(Lowest Common Ancestor)
定义
在树上取两点 x,yx,y,他们的 LCA 为距离他们最近的公共祖先。
本章主要讲的是倍增求 LCA。
暴力求取
- 从 xx 开始向上移动到根结点,并标记沿途结点。
- 从 yy 开始向上移动到根结点,第一个被标记的就是 xx 和 yy 的 LCA。
倍增求 LCA
从任意点对 (x,y)(x,y) 移到 xx 和 yy 的 LCA 的距离可拆分为 22 的幂的和。
若预处理任意点 xx 移动 22 的幂步所到达的结点编号,则不超过 \log_2{n}log2n 次即可找到 LCA。
具体实现
first:预处理倍增 DP
定义状态 dp_{i,j}dpi,j 表示点 ii 向上移动 2^j2j 步到达的结点编号。
状态转移方程:枚举 jj 从 11 到 \log_2 nlog2n,dp_{i,j}=dp_{dp_{i,j-1},j-1}dpi,j=dpdpi,j−1,j−1。
初始状态:dp_{i,0}=fa_idpi,0=fai。
代码片段
void pre_lca(int cur, int fa)
{dep[cur]=dep[fa]+1;dp[cur][0]=fa;for(int i=1;(1<<i)<=dep[cur];i++){dp[cur][i]=dp[dp[cur][i-1]][i-1];}for(int nxt:nbr[cur]){if(nxt!=fa)pre_lca(nxt,cur);}
}second:处理单次询问
第一步:约定深度较大的点,若 dep_x>dep_ydepx>depy,交换 xx 和 yy。
第二步:将深度较大的结点 yy 倍增向上跳至深度等于 xx。
第三步:判断 xx 是否等于 yy。若已经相等则 xx 为 LCA,停止寻找。
第四步:xx 和 yy 一起倍增向上跳,只要 xx 和 yy 不重合。
第五步:xx 向上一步即为 LCA。
代码片段
int lca(int x, int y)
{if(dep[y]<dep[x])swap(x,y);for(int i=20;i>-1;i--){if(dep[dp[y][i]]>=dep[x]){y=dp[y][i];}}if(x==y)return x;for(int i=20;i>-1;i--){if(dp[x][i]!=dp[y][i]){x=dp[x][i],y=dp[y][i];}}return dp[x][0];
}时间复杂度
预处理是 O(n \log_2 n)O(nlog2n) 的,中间单次求取仅为 O(n)O(n)
模板代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
int dp[500005][21],dep[500005], n, m, s;
vector<int> nbr[500005];
void pre_lca(int cur, int fa)
{dep[cur]=dep[fa]+1;dp[cur][0]=fa;for(int i=1;(1<<i)<=dep[cur];i++){dp[cur][i]=dp[dp[cur][i-1]][i-1];}for(int nxt:nbr[cur]){if(nxt!=fa)pre_lca(nxt,cur);}
}
int lca(int x, int y)
{if(dep[y]<dep[x])swap(x,y);for(int i=20;i>-1;i--){if(dep[dp[y][i]]>=dep[x]){y=dp[y][i];}}if(x==y)return x;for(int i=20;i>-1;i--){if(dp[x][i]!=dp[y][i]){x=dp[x][i],y=dp[y][i];}}return dp[x][0];
}
signed main()
{ios::sync_with_stdio(0),cin.tie(0);cin>>n>>m>>s;for(int i=1;i<n;i++){int x, y;cin>>x>>y;nbr[x].push_back(y);nbr[y].push_back(x);}pre_lca(s,0);for(int i=1;i<=m;i++){int x, y;cin>>x>>y;cout<<lca(x,y)<<"\n";}
}LCA 应用
- 求树上两点之间距离。
- 树上差分。
LCA 求树上两点之间距离
维护 dis_xdisx 表示根结点到 xx 的距离。
xx 到 yy 的简单路径的长度为 dis_x+dis_y-2\times dis_{\texttt{lca}(x,y)}disx+disy−2×dislca(x,y)。
LCA 例题
first:P5836
方法 1
点权可以转为 00 或 11,维护 dis_idisi 表示由根结点到 ii 的距离。
维护深度 dep_idepi,对于每次询问,若 (dis[a]+dis[b]-2*dis[lcad]+w[lcad]==dep[a]+dep[b]-2*dep[lcad]+1)&&c!='H' 或 dis[a]+dis[b]-2*dis[lcad]+w[lcad]==0&&c=='H' 则输出 00,否则输出 11。
方法 2
若一条边的两个端点的 ww 相同,则 unionn 这两个端点。
若一条路径上点权相同,则两个端点一定在同一集合。若该集合的权值不等于询问,输出 00,否则输出 11。
while(m--)
{int x, y;char c;cin>>x>>y>>c;if(c=='H'){cout<<!(find(x)==find(y)&&w[x]==0);}else{cout<<!(find(x)==find(y)&&w[x]==1);}
}方法 3
维护 dp_{i,j}dpi,j 表示 ii 向上动 2^j2j 步到达的结点编号,维护 yes_{i,j,0/1}yesi,j,0/1 表示 ii 向上跳 2^j2j 步是否有 ww 为 0/10/1 的点。
yes[cur][i][0]=yes[cur][i-1][0]|yes[dp[cur][i-1]][i-1][0],yes[cur][i][1]=yes[cur][i-1][1]|yes[dp[cur][i-1]][i-1][1];。
初始状态:dp_{i,0}=fa_idpi,0=fai,yes_{i,0,w_{fa}}=1yesi,0,wfa=1。
second:CF519E
若 AA 到 BB 的距离为奇数,则答案直接为 00。
否则分情况讨论:
-
中间位置的点 x=lcax=lca
xx 儿子结点中包含 AA 和 BB 的子树剔除,其余为答案。
-
中间位置的点 xx 不是 lcalca
约定深度较大的点为 BB,找到 BB 向上距离 xx 一步的点 pp,则答案为 size_x-size_psizex−sizep。
注意特殊情况:A==BA==B 时,答案为 nn。
从 lcalca 到 xx 的距离为 \frac{dep_B-dep_A}{2}2depB−depA。
void work(int x,int y)
{if(x==y){cout<<n<<"\n";return ;}if(dep[x]==dep[y]){for(int i=14;i>=0;i--){if(dp[x][i]!=dp[y][i]){x=dp[x][i],y=dp[y][i];}}cout<<size[1]-size[x]-size[y]<<"\n";return ;}if(dep[x]<dep[y]) swap(x,y);if((dep[x]-dep[y])%2==1){cout<<"0\n";return ;}int x2=x,len=(dep[x]-dep[y])/2;for(int i=14;i>=0;i--){if(dep[dp[x][i]]>=dep[y]){x=dp[x][i];}}if(x==y){len+=dep[x];for(int i=14;i>=0;i--){if(dep[dp[x2][i]]>len){x2=dp[x2][i];}}cout<<size[dp[x2][0]]-size[x2]<<"\n";return ;}for(int i=14;i>=0;i--){if(dp[x][i]!=dp[y][i]){x=dp[x][i],y=dp[y][i];}}len+=dep[x]-1;for(int i=14;i>=0;i--){if(dep[dp[x2][i]]>len){x2=dp[x2][i];}}cout<<size[dp[x2][0]]-size[x2]<<"\n";
}Third:P8972 一切都已过去
见 题解:P8972 『GROI-R1』 一切都已过去 - 洛谷专栏
方便阅读搬过来。
从数据范围很容易发现,如果我们把边权累乘再判整数,炸掉是必然的,这时候,我们来发现一个性质:只有小数部分有 22 和 55 相乘的时候,才可能变成整数。当然,这并不是绝对的,例如 2.02 \times 52.02×5 就不是整数。从上面举的例子很容易发现一个性质:两个实数的乘积是否为整数与小数点数位也有关系。一对 22 和 55 可以抵消掉一个小数点数位(22 和 55 可以在任意且不同数位上,并且 22 和 55 的倍数也有用)。这时,我们可以将边权通过不断 \times 10×10 变成整数,并分解质因数分别求因数中 22 和 55 的个数(点权也要处理)。22 和 55 的个数求出来了,小数点数位也很好处理。最终的小数点位数应该是所有路径上的边权小数点位数之和,所以我们在将边权化整数时再维护一个变量统计小数点位数并记录到邻接矩阵里。若路径 xx 到 yy 的总边权乘上 xx 的点权得到的结果中 22 的个数和 55 的个数大于或等于总小数点位数,则其为整数。分别维护即可。
注意:若边权或点权为 00 则对应维护的当前点权或点权的 22 和 55 赋予极大值。
Latex有双倍问题,完整版请在安全访问中心 - 洛谷查看
相关文章:
)
LCA(Lowest Common Ancestor)
LCA(Lowest Common Ancestor) 定义 在树上取两点 x,yx,y,他们的 LCA 为距离他们最近的公共祖先。 本章主要讲的是倍增求 LCA。 暴力求取 从 xx 开始向上移动到根结点,并标记沿途结点。从 yy 开始向上移动到根结点,…...

张钹院士:大模型时代的企业AI发展趋势
在当今技术迅速发展的时代,生成式人工智能与大模型正成为推动产业变革的重要力量。随着AI技术的不断成熟与普及,它的应用已从个人领域扩展至企业层面,广泛覆盖各行各业。 那么,新技术究竟会给产业带来哪些积极地影响?…...

php连接sphinx的长连接事宜以及sphinx的排除查询以及关于sphinx里使用SetSelect进行复杂的条件过滤或复杂查询
一、php连接sphinx的长连接事宜以及sphinx的排除查询 在使用php连接sphinx时,默认的sphinx连接非长连接,于是在想php连接sphinx能否进行一些优化 publish:January 9, 2018 -Tuesday: 方法:public bool SphinxClient::open ( void ) — 建立到…...

抓包分析排查利器TCPdump
tcpdump命令介绍与常规用法。 基础命令介绍 # 固定语法 -i 指定网卡名称 -nn 显示IP地址 -w 指定输出的文件名称 tcpdump -i eth0 -nn -w test.cap-nn 不把主机的网络地址与协议转换成名字 -w 把数据包数据写入指定的文件 and 连接参数 host 指明主机 port 指明端口 src 源IP…...

八种排序算法的复杂度(C语言)
归并排序(递归与非递归实现,C语言)-CSDN博客 快速排序(三种方法,非递归快排,C语言)-CSDN博客 堆排序(C语言)-CSDN博客 选择排序(C语言)以及选择排序优化-CSDN博客 冒泡排序(C语言)-CSDN博客 直接插入排序(C语言)-CSDN博客 希尔排序( 缩小增量排序 )(C语言)-CSDN博客 计数…...

docker compose部署rabbitmq集群,并使用haproxy负载均衡
一、创建rabbitmq的data目录 mkdir data mkdir data/rabbit1 mkdir data/rabbit2 mkdir data/rabbit3 二、创建.erlang.cookie文件(集群cookie用) echo "secretcookie" > .erlang.cookie 三、创建haproxy.cfg配置文件 global log stdout fo…...

git强制推送代码教程
git强制推送代码教程 首先说明情况,我的代码remote了两个git库,现在想要推送到其中一个,但是版本不对,被拒绝,因此下面将进行强制推送 首先检查远程库都有哪些 git remote -v2. 检查当前的分支 git branch当前分支前…...
)
windows C++-高级并发和异步(三)
深入了解 winrt::resume_foreground(下) 调用 winrt::resume_foreground 时会始终先排队,然后展开堆栈。 也可选择设置恢复优先级。 winrt::fire_and_forget RunAsync(DispatcherQueue queue) {...co_await winrt::resume_foreground(queue, DispatcherQueuePrior…...
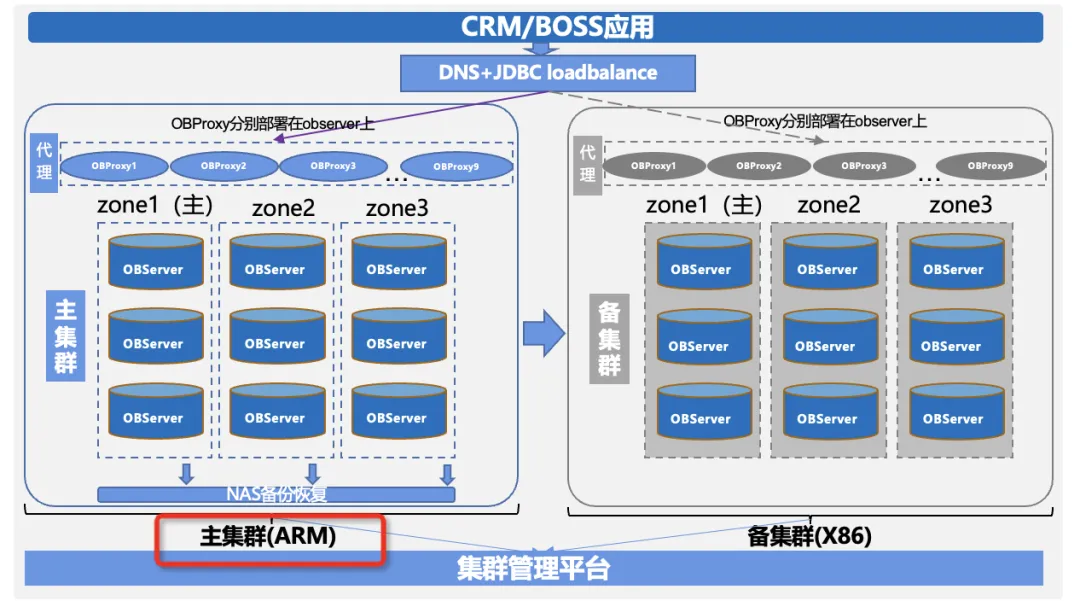
河北移动:核心系统数据库成功完成整体迁移 ,实现全栈国产|OceanBase案例
本文作者:移动通信集团河北有限公司架构规划专家,房瑞 项目背景: 中国移动通信集团河北有限公司一直在积极响应国家及集团的号召,以磐舟&磐基云原生为底座,结合国产浏览器、中间件、数据库、操作系统和服务器等&a…...

ZKRollup
目录 ZKRollup 基本概念 运作原理 特点与优势 应用场景 典型项目 ZKRollup ZKRollup,全称为Zero-Knowledge Rollup,是一种基于零知识证明的二层扩容方案(Layer 2)。它旨在通过提高交易处理效率和降低交易成本来扩展区块链网络的能力,尤其是在以太坊等区块链平台上得…...

letcode 分类练习 树的遍历
letcode 分类练习 树的遍历 树的构建递归遍历前序遍历中序遍历后序遍历 迭代遍历前序遍历中序遍历后序遍历 层序遍历层序遍历可以解决的问题107. 二叉树的层序遍历 II199. 二叉树的右视图637. 二叉树的层平均值429. N 叉树的层序遍历515.在每个树行中找最大值116.填充每个节点的…...

redisssion分布式锁
分布式锁的问题 基于setnx的分布式锁实现起来并不复杂,不过却存在一些问题。 锁误删问题 第一个问题就是锁误删问题,目前释放锁的操作是基于DEL,但是在极端情况下会出现问题。 例如,有线程1获取锁成功,并且执行完任…...

嘎嘎嘎拿到去年想要的包
一年多了 继续,把项目收尾吧 好好学前端,外企!react!从0开始,紧迫!加油!...
前奏编曲:如何编写二段式前奏
选好音源 Pianoteq 6 STAGE比较明亮些,适合做前奏的音源 确定和弦进行 比如4536251,每个小节2和弦,每个小节的和弦弹一下 优化和弦进行衔接和织体 二段式不用对和弦进行就近解决的处理,因为前奏前后要形成对比。 前半部分往…...

征服云端:Kubernetes如何让微服务与云原生技术如虎添翼
引言 在这个数字化转型的时代,微服务架构已经成为构建现代应用程序的首选方式。它不仅提高了开发效率,还增强了系统的可扩展性和灵活性。而随着云计算技术的迅猛发展,云原生的概念逐渐深入人心,它代表了一种全新的软件开发方法论…...

开源AI智能名片系统与高级机器学习技术的融合应用:重塑商务交流的未来
摘要:在数字化浪潮的推动下,人工智能(AI)技术,尤其是机器学习领域的快速发展,正深刻改变着各行各业的面貌。开源AI智能名片系统作为这一变革的先锋,通过集成并优化多种高级机器学习技术…...

Java中synchronized的偏向锁是如何减少锁开销的
偏向锁(Biased Locking)是一种优化 Java synchronized 锁的机制,旨在减少在无竞争情况下的锁开销。它通过将锁偏向于单个线程来优化锁的性能。以下是偏向锁减少锁开销的具体方式和原理: 偏向锁的工作原理 锁的初始状态: 当一个对…...

react18 + ts 使用video.js 直播.m3u8格式的视频流
一、安装依赖 我使用的video.js版本是8.17.3,从 Video.js 7.x 开始,HLS 支持被内置到了 Video.js 中所以不需要安装其他依赖 npm i video.js 二、创建VideoPlayer组件 import React, { useEffect, useRef } from react import videojs from video.js …...

使用 onBeforeRouteLeave 组合式函数提升应用的用户体验
title: 使用 onBeforeRouteLeave 组合式函数提升应用的用户体验 date: 2024/8/14 updated: 2024/8/14 author: cmdragon excerpt: 摘要:本文介绍了在Nuxtjs中使用onBeforeRouteLeave组合式函数来提升应用用户体验的方法。onBeforeRouteLeave允许在组件离开当前路…...

uni-app 吸顶方案总结
效果 页面级 uni.pageScrollTo 官方文档:https://uniapp.dcloud.net.cn/api/ui/scroll.html#pagescrollto 原生头部导航 uni.pageScrollTo({selector: #tabs,duration: 300 });(推荐)需要兼容自定义头部导航 <template><view id"demo1" :styl…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
