数据结构——时间复杂度和空间复杂度
目录
时间复杂度
什么是时间复杂度
常见时间复杂度类型
如何计算时间复杂度
空间复杂度
什么是空间复杂度
常见的空间复杂度类型
如何计算空间复杂度
时间复杂度和空间复杂度是评估算法性能的两个重要指标。
时间复杂度
什么是时间复杂度
时间复杂度描述了算法执行所需时间随输入规模增长的变化趋势。它通常用大O表示法来描述,表示算法在最坏情况下的时间性能。
常见时间复杂度类型
- 常数时间:O(1)。算法执行时间不随输入规模的变化而变化。
- 线性时间:O(n)。算法执行时间与输入规模成正比。
- 平方时间:O(n^2)。算法执行时间与输入规模的平方成正比,通常见于嵌套循环。
- 对数时间:O(logn)。算法执行时间随输入规模的增长而缓慢增加,常见于分治和二分查找算法。
- 线性对数时间:O(nlogn)。算法执行时间是输入规模与对数的乘积,常见于快速排序或归并排序。
- 指数时间:O(2^n)。算法执行时间随输入规模指数增长,常见于暴力搜索。
在大O表示法中,logn一般指的是以2为底的对数,因为绝大部分都只用考虑二分的情况,以其他数为底的情况很少出现。
如何计算时间复杂度
exp.1
//Func1的时间复杂度为O(N)
void Func1(int N)
{int i = 0;int count = 0;for (i = 0; i < N; i++){++count;}int m = 10;while (m){--m;}printf("%d\n",count);
}
该函数的运行时间主要跟输入的N的大小有关,故为O(n)的时间。
至于说下面的执行的m次循环,我们是不用理会的,因为在输入的N很大的情况,m次循环可以被忽略掉。我们算时间复杂度都是关注主要最主要的部分,比如说O(n^2 + 2n), 那么时间复杂度是O(n^2)。
exp.2
//Func2的时间复杂度为O(N)
void Func2(int N)
{int count = 0;int i = 0;for (i = 0; i < N; i++){++count;}for (i = 0; i < N; i++){++count;}printf("%d\n",count);
}
这里咋一看时间复杂度是O(2n),但其实时间复杂度还是O (n)。
计算机运行的时间是非常快的,所以即使n非常大,n的常系数对于整个函数的运行时间是微乎其微的。
所以算时间复杂度也不用算n的常系数。
exp.3
//Func3的时间复杂度为O(1)
void Func3()
{int count = 0;int i = 0;for (i = 0; i < 100; i++){++count;}printf("%d\n",count);
}时间复杂度为O(1),因为是常数次运行。
exp.4
// BubbleSort的时间复杂度为O(N^2)
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
外层循环执行n次,内层循环执行n-1次、n-2次...等,等差乘等比,最会算出来会有n^2,所以时间复杂度是O(n^2)。
exp.5
// BinarySearch的时间复杂度O(logN)
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;while (begin < end){int mid = begin + ((end - begin) >> 1);//使用右移操作符相当于除以2if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid;elsereturn mid;}return -1;
}
二分查找的时间复杂度是O(logn),就是对n取以二为底的对数。
exp.6
// 阶乘递归Fac的时间复杂度为O(N)
long long Fac(size_t N)
{if (0 == N)return 1;return Fac(N - 1) * N;
}
递归的次数同样也算进时间复杂度,这里递归了n次,所以时间复杂度是O(n)。
这里的空间复杂度也是O(n),因为递归调用函数会在栈上多开n块额外的空间。
exp.7
// 斐波那契递归Fib的时间复杂度为O(2^N)
long long Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
以这种方法算斐波那契数列的递归调用次数,有点类似算完全二叉树的节点个数。
所以时间复杂度是O(2^n)。
总结
时间复杂度只需大概想想执行次数n的表达式,取次数最大的那项,也不用理会n的常系数。
如果涉及递归,要想想递归函数的执行次数。

空间复杂度
什么是空间复杂度
空间复杂度描述了算法执行过程中所需的额外存储空间量,也用大O表示法来描述。
常见的空间复杂度类型
- 常数空间:O(1)。算法使用固定数量的额外空间,与输入规模无关。
- 线性空间:O(n)。算法使用的额外空间与输入规模成正比。
- 平方空间:O(n^2)。算法使用的额外空间与输入规模的平方成正比。
- 对数空间:O(logn)。算法使用的额外空间随输入规模的增长而缓慢增加。
- 线性对数空间:O(nlogn)。算法使用的额外空间是输入规模与对数的乘积。
如何计算空间复杂度
exp.1
//sum的空间复杂度是O(1)
int sum(int n) {int sum = 0;for (int i = 0; i < n; i++) {sum += i;}return sum;
}sum只额外开辟变量sum,额外开辟的空间跟输入的n无关,所以空间复杂度是O(1)
exp.2
//Func的空间复杂度是O(n)
void Func(int n)
{int* arr = (int*)malloc(sizeof(int) * n);//....}Func使用的空间复杂度是O(n),因为额外开辟的空间与n成正比。
总结
计算空间复杂度只需看使用的额外存储空间与输入数据规模大小的关系,比如,跟规模无关就是O(1),跟规模成正比就是O(n),其他O(n^2)等同理。
拜拜,下期再见😏
摸鱼ing😴✨🎞

相关文章:

数据结构——时间复杂度和空间复杂度
目录 时间复杂度 什么是时间复杂度 常见时间复杂度类型 如何计算时间复杂度 空间复杂度 什么是空间复杂度 常见的空间复杂度类型 如何计算空间复杂度 时间复杂度和空间复杂度是评估算法性能的两个重要指标。 时间复杂度 什么是时间复杂度 时间复杂度描述了算法执行所需…...

(echarts) 饼图设置滚动图例
(echarts) 饼图设置滚动图例 效果: 代码: // 图例 legend: {type: scroll,orient: vertical,right: 10,top: 20,bottom: 20,data: data.legendData},参考:官网-可滚动的图例 https://echarts.apache.org/examples/zh/editor.html?cpie-leg…...

Java spring SSM框架--mybatis
一、介绍 Spring 框架是一个资源整合的框架,可以整合一切可以整合的资源(Spring 自身和第三方),是一个庞大的生态,包含很多子框架:Spring Framework、Spring Boot、Spring Data、Spring Cloud…… 其中Spr…...

Python知识点:如何使用Arduino与Python进行物联网项目
Arduino和Python是物联网(IoT)项目中常用的两种技术。Arduino是一个开源的硬件平台,而Python是一种高级编程语言,它们可以结合使用来创建各种智能设备和系统。以下是使用Arduino和Python进行物联网项目的一般步骤: 确定项目需求: …...

论文复现_从 CONAN 中收集 TPL 数据集
1. 概述 CONAN:Conan是一个用于C项目的开源包管理工具。 它的主要目标是简化C项目的依赖关系管理过程,使开发人员能够更轻松地集成、构建和分享C库。 其中有一些比较独特的功能,例如:版本管理、第三方库管理等。 TPL 数据集&…...

使用Docker将Java项目打包并部署到CentOS服务器的详细教程。
当然,让我们将上述步骤进一步细化,以便更好地理解整个过程。 前提条件 一个Java项目CentOS服务器,并且已安装DockerJava项目可以正常在本地运行具有服务器访问权限 ———————————————————————————————————…...

嘉立创eda布线宽度
https://prodocs.lceda.cn/cn/pcb/route-routing-width/#%E5%B8%83%E7%BA%BF%E5%AE%BD%E5%BA%A6...

硬件面试经典 100 题(31~50 题)
31、多级放大电路的级间耦合方式有哪几种?哪种耦合方式的电路零点偏移最严重?哪种耦合方式可以实现阻抗变换? 有三种耦合方式:直接耦合、阻容耦合、变压器耦合。直接耦合的电路零点漂移最严重,变压器耦合的电路可以实现…...

5G:下一代无线通信技术的全面解析
随着科技的不断进步,移动通信技术也在飞速发展。从2G到4G,我们见证了无线网络的巨大变革,而现在,5G已经悄然来临。作为下一代无线通信技术,5G不仅将带来更快的速度和更低的延迟,还将开启全新的应用场景和商…...

关于refresh_token
前文介绍过jwt的一般使用场景,用户登录成功后获得jwt,其中包含用户相关信息,主要是在前端要用到的属性(比如姓名、应用角色[这个前端后都用得着]等)、在后端要用到的属性(比如登录IP、终端唯一标识…...

Linux网络:基于OS的网络架构
Linux网络:OS视角下的网络架构 网络分层模型OSI 七层模型TCP/IP 五层模型 协议操作系统与网络网络相关命令ifconfigpingnetstat 本博客将基于操作系统,讲解计算机网络的设计理念,帮助大家理解操作系统与网络之间的关系。 网络分层模型 网络…...

UEC++学习(十六)变量添加中文注释、ui设置中文文本
(一)变量添加中文注释 在C 项目中创建变量,并在蓝图中显示变量的英文名同时附带中文注释,可以使用UPROPERTY 的 ToolTip 元数据属性来实现 UPROPERTY(EditAnywhere, meta (ToolTip "弹夹最大容量"))int32 MagCapacit…...

Redis延迟双删
1、何为延时双删 Redis延迟双删是一种在数据更新操作中确保缓存与数据库数据一致性的策略,通过两次缓存删除操作间隔一段延时来减少数据不一致的问题。 在并发环境下,多个请求同时对同一数据进行读写时,如果没有妥善处理,很容易…...

WO Mic 手机变身免费麦克风
目录 一、主要特点 1.支持多种连接方式 2.应用广泛 3.低延迟 4.简易配置 5.自动连接 6.音频格式 二、软件下载 三、软件安装 四、系统连接 五、测试 直播的时候,上课的时候,会议的时候……突然发现没有麦克风或者电脑麦克风有故障,这可怎么办呢?今天给大家介绍一…...

MQ死信对列
面试题:你们是如何保证消息不丢失的? 1、什么是死信 死信就是消息在特定场景下的一种表现形式,这些场景包括: 1. 消息被拒绝访问,即消费者返回 basicNack 的信号时 或者拒绝basicReject 2. 消费者发生异常࿰…...

springboot乡镇小区管理系统-计算机毕业设计源码73685
摘 要 过去使用手工的管理方式对乡镇小区进行管理,造成了管理繁琐、难以维护等问题,如今使用计算机对停车场停车的各项基本信息进行管理,比起手工管理来说既方便又简单,而且具有易于管理、搜索速度快、存储量大等多个优点。将其使…...

基于vue框架的4S店汽车维修保养管理系统28a7y(程序+源码+数据库+调试部署+开发环境)系统界面在最后面。
系统程序文件列表 项目功能:客户,技师,车辆信息,财务,客户维修,维修分配,维修订单,保养预约,保养分配,保养订单,维修费用,保养费用 开题报告内容 基于Vue框架的4S店汽车维修保养管理系统 开题报告 一、项目背景与意义 随着汽车产业的迅猛发展,4S店作…...
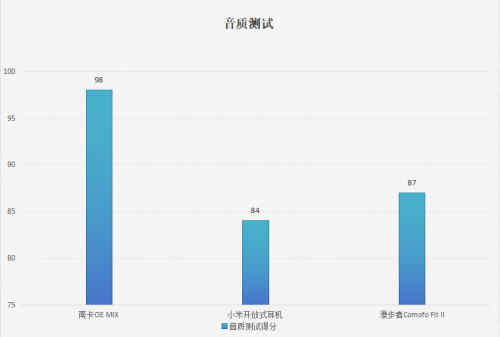
小米开放式耳机值得买吗?南卡、小米、漫步者一周横评
大家好,最近对开放式耳机比较感兴趣,作为一名数码博主以及多年的耳机发烧友,今天想给大家测评一下开放式耳机,这类耳机目前在数码圈非常火热!很多喜欢运动的小伙伴都选择了这款耳机,搭配运动场景听歌&…...

解决oracel锁表问题;SQL 错误 [54] [61000]: ORA-00054: 资源正忙
问题描述; SQL 错误 [54] [61000]: ORA-00054: 资源正忙, 但指定以 NOWAIT 方式获取资源, 或者超时失效 select session_id from v$locked_object;查看这些 session_id 对应的会话的详细信息,包括用户名、机器名、程序等,9596等是select se…...

Jfinal与hibernate-validator实现后台表单
一. pom.xml配置 jfianl maven项目基础上增加 <dependency><groupId>org.hibernate</groupId><artifactId>hibernate-validator</artifactId><version>${hibernate-validator.version}</version></dependency><dependency…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 )
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
