【DFS专题】深度优先搜索 “暴搜”优质题单推荐 10道题(C++ | 洛谷 | acwing)
文章目录
- 题单
- 一、模板 [极为重要]
- 全排列DFS
- 组合型DFS
- 指数DFS
- 二、专题
- 烤鸡 (指数BFS)
- P1088 火星人 【全排列】
- P1149 火彩棒 [预处理 ]
- P2036 PERKET
- P1135 奇怪的电梯 暴力
- P1036 [NOIP2002 普及组] 选数 (组合)
- P1596 [USACO10OCT]Lake Counting S 【DFS求图的连通块】
- 八数码
【DFS专题】优质题单推荐 10道题(C++ | 洛谷 | acwing)
题单
- 来自b站大佬的题单
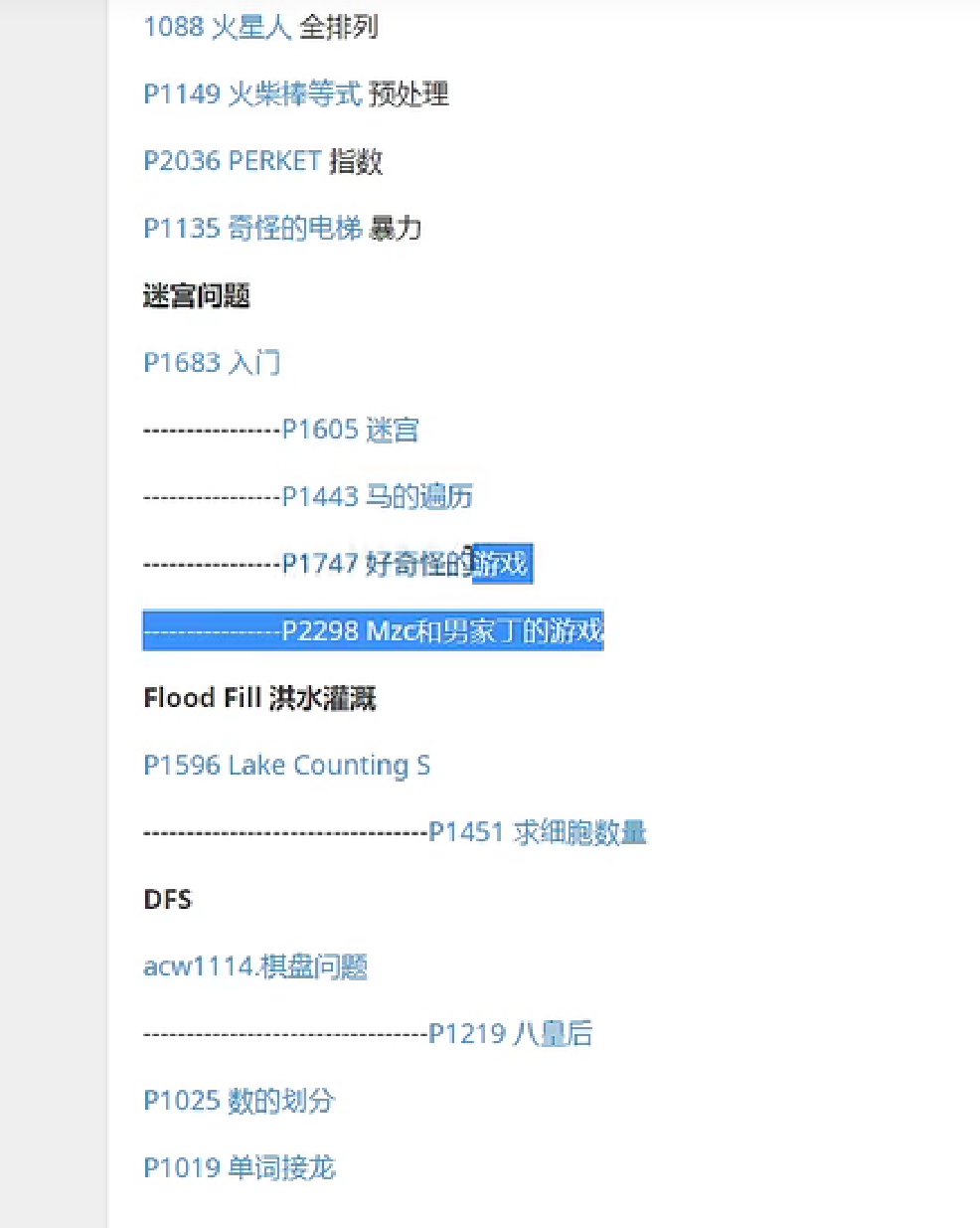
一、模板 [极为重要]
全排列DFS
- 每个位置选什么数
#include<iostream>
using namespace std;
const int N = 10;
int path[N];//保存序列
int state[N];//数字是否被用过
int n;
void dfs(int u)
{if(u > n)//数字填完了,输出{for(int i = 1; i <= n; i++)//输出方案cout << path[i] << " ";cout << endl;}for(int i = 1; i <= n; i++)//空位上可以选择的数字为:1 ~ n{if(!state[i])//如果数字 i 没有被用过{path[u] = i;//放入空位state[i] = 1;//数字被用,修改状态dfs(u + 1);//填下一个位state[i] = 0;//回溯,取出 i}}
}int main() {cin >> n;dfs(1);
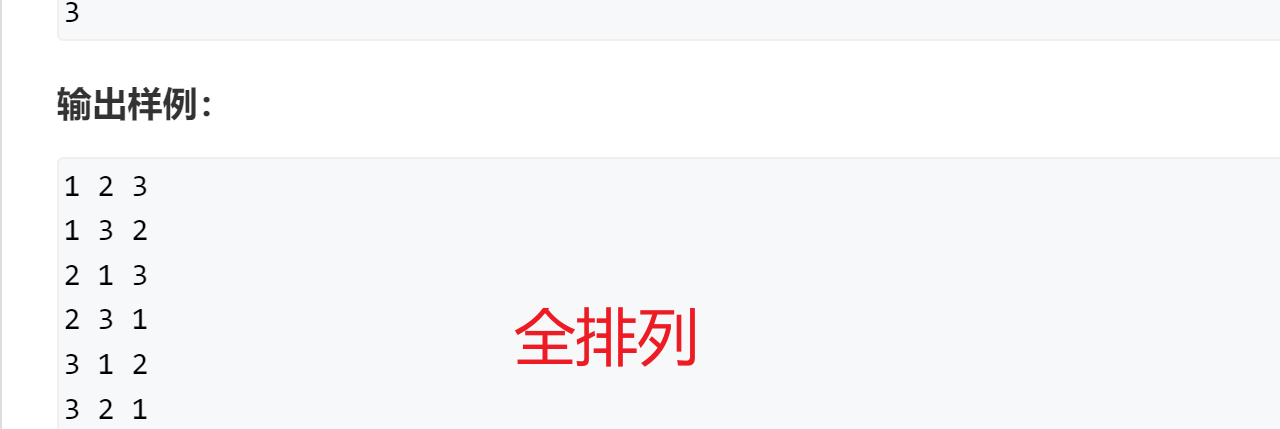
}组合型DFS
- 与全排列的差别就是第二个for循环开始的位置,换句话说就是每个数该放什么位置。
#include <bits/stdc++.h>
using namespace std;
const int N = 30;
int path[N];
int n, m;void dfs (int u, int start ) {//u:层数 start:起始的数值if (u > m) {for (int i = 1; i <= m; i ++ ) {cout << path[i] << ' ';}puts("");}else {for (int i = start; i <= n; i ++) {//path[u] = i;//表示已经填了dfs(u + 1, i + 1);//递归下一层path[u] = 0;//恢复现场}}
} int main () {cin >> n >> m;dfs(1,1); //第一层开始 且从1开始枚举return 0;
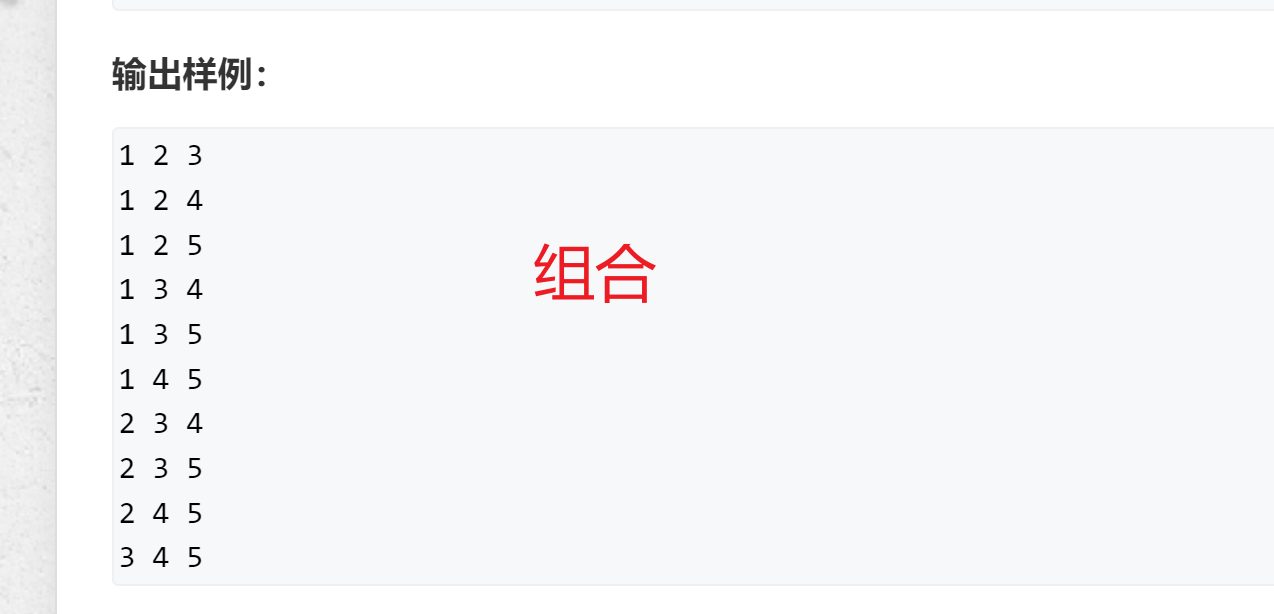
}指数DFS
- 参数 : 前u个数 选 or 不选 的
- 需要保存第x位置的状态的时候就需要用st数组来存状态
- int st[] 0:没有遇见 1 选 2不选
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 16;
int st[N];
int n;
void dfs (int u) {//u :层数if (u > n) {//叶子结点for (int i = 1; i <=n; i ++ ){if (st[i] == 1) {//如果选了 就输出 1选 2不选cout << i << ' ';}}puts("");return ;}st [u] = 1;//选dfs (u + 1);//递归下一层st[u] = 0;//回溯st[u] = 2;//不选dfs (u+1);//递归下一层st[u] = 0;//回溯 【恢复现场】
}
int main () {cin >> n;dfs(1);return 0;
}二、专题
烤鸡 (指数BFS)
- 每个方案有3种选择,枚举全部则有 310 种方案数
https://www.luogu.com.cn/problem/P2089
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20;
int n;
int arr[N]; // 存储临时答案
int res = 0;// 方案数量
int mem[60000][N]; // 存储总方案数
// 60000 >= 3^10 (最多枚举数量)// x : 当前枚举到哪个数 sum : 当前总和
void dfs(int x, int sum ) {if(sum > n) return ;// 剪枝if(x > 10) {if(sum == n) {res ++;for(int i = 1; i <= 10; i ++) {mem[res][i] = arr[i];}}return;}for(int i = 1; i <= 3; i ++) {arr[x] = i;dfs(x + 1, sum + i);arr[x] = 0; // 恢复现场}
}int main () {cin >> n;dfs(1, 0);printf("%d\n" , res);for (int i = 1; i <= res; i ++ ) {for(int j = 1; j <= 10; j ++) {printf("%d ", mem[i][j]);}printf("\n");}return 0;
}
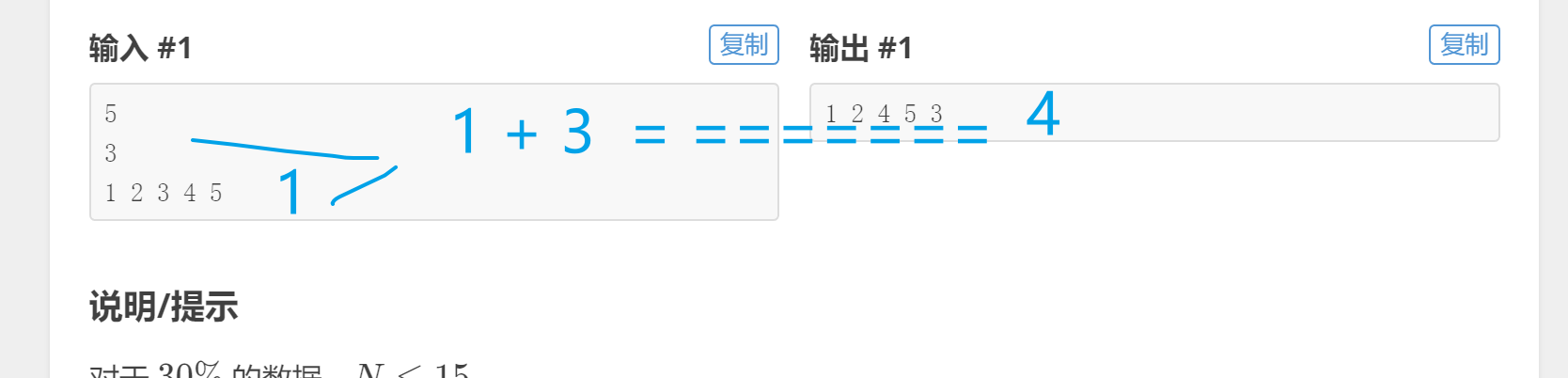
P1088 火星人 【全排列】
- https://www.luogu.com.cn/problem/P1088

- 为什么要 m + 1
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 10010;
int n, m;
int res = 0;
int ans[N], a[N];
bool st[N];
bool flag = false;
void dfs(int x) {if(flag) return; //剪枝 因为只会输出一次结果if(x > n) {res ++;if(res == m + 1) {for(int i = 1; i <= n; i ++ ){printf("%d ", ans[i]);}flag =true;}return ;}for (int i = 1; i <= n; i ++ ){if(!res) {i = a[x]; // 起点}if(! st[i]) {st[i] = true;ans[x] = i;dfs(x + 1);ans[x] = 0;st[i] = false;}}
}int main () {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);;dfs(1);return 0;
}
P1149 火彩棒 [预处理 ]
https://www.luogu.com.cn/problem/P1149

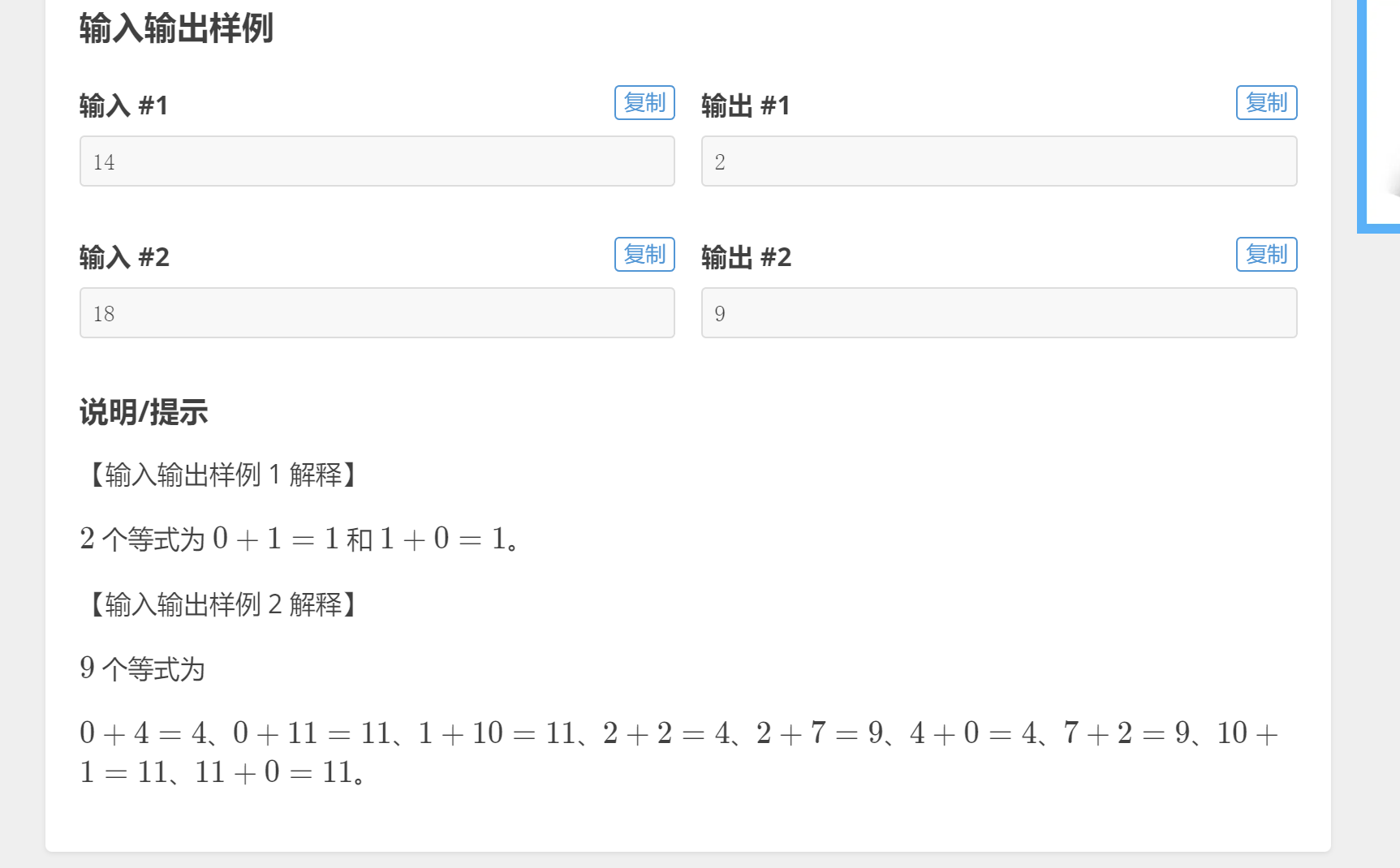
- 思路一 、 模拟

- 思路二 :预处理 + dfs 枚举
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 100010;int n;
int res = 0;
int s[N];
int num[N] = {6,2,5,5,4,5,6,3,7,6};void dfs(int x, int sum) {if(sum > n ) return ;if(x > 3) {if(s[1] + s[2] == s[3] && sum == n) {res ++;}return ;}//枚举前 1000for(int i = 0; i <= 1000; i ++) {s[x] = i;dfs(x + 1, sum + num[i]) ;s[x] = 0;}
}int main () {scanf("%d", &n);n -= 4;//递推求前1000个数for (int i = 10; i <= 1000; i ++ ) {num[i] = num[i % 10] + num[i / 10];}dfs(1, 0);printf("%d\n" , res);return 0;
}
P2036 PERKET

#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 20;int n;
int res = 1e9;
int s[N], k[N];
int st[N]; // 0 表示没考虑 1 选 2 不选void dfs(int x) {if(x > n) {bool first = false; // 如果没选就不计算resint sum1 = 1;//酸的积int sum2 = 0; // 苦的和for (int i = 1; i <= n; i ++ ) {if(st[i] == 1) {sum1 *= s[i];sum2 += k[i];first = true;}}if(first) {res = min(res, abs(sum1 - sum2));}return ;}st[x] = 1;dfs(x + 1);st[x] = 0;st[x] = 2;dfs(x + 1);st[x] = 0;
}int main () {scanf("%d", &n);for (int i = 1; i <= n; i ++ ) scanf("%d%d", &s[i], &k[i]);;dfs(1);printf("%d\n" , res);return 0;
}
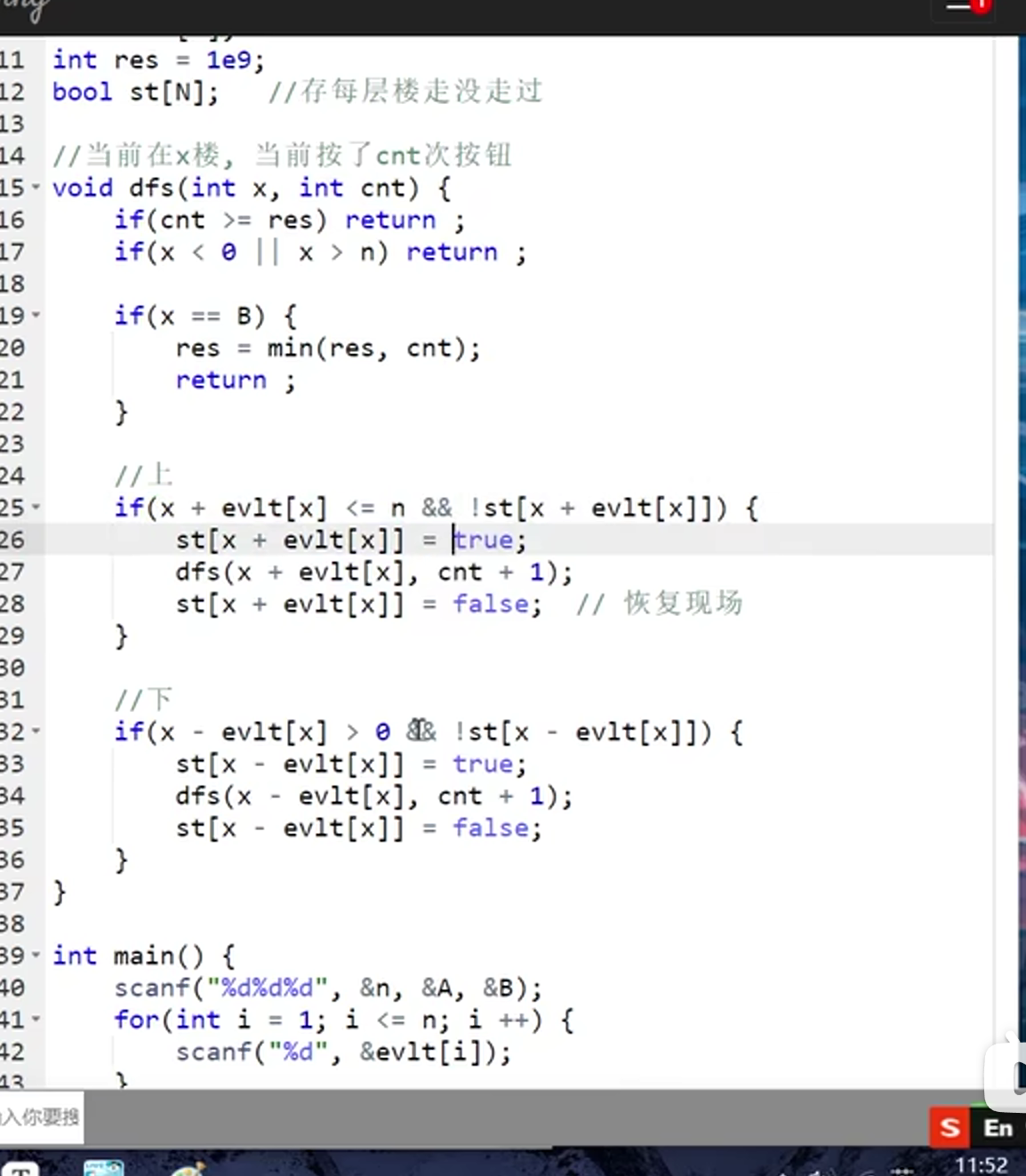
P1135 奇怪的电梯 暴力
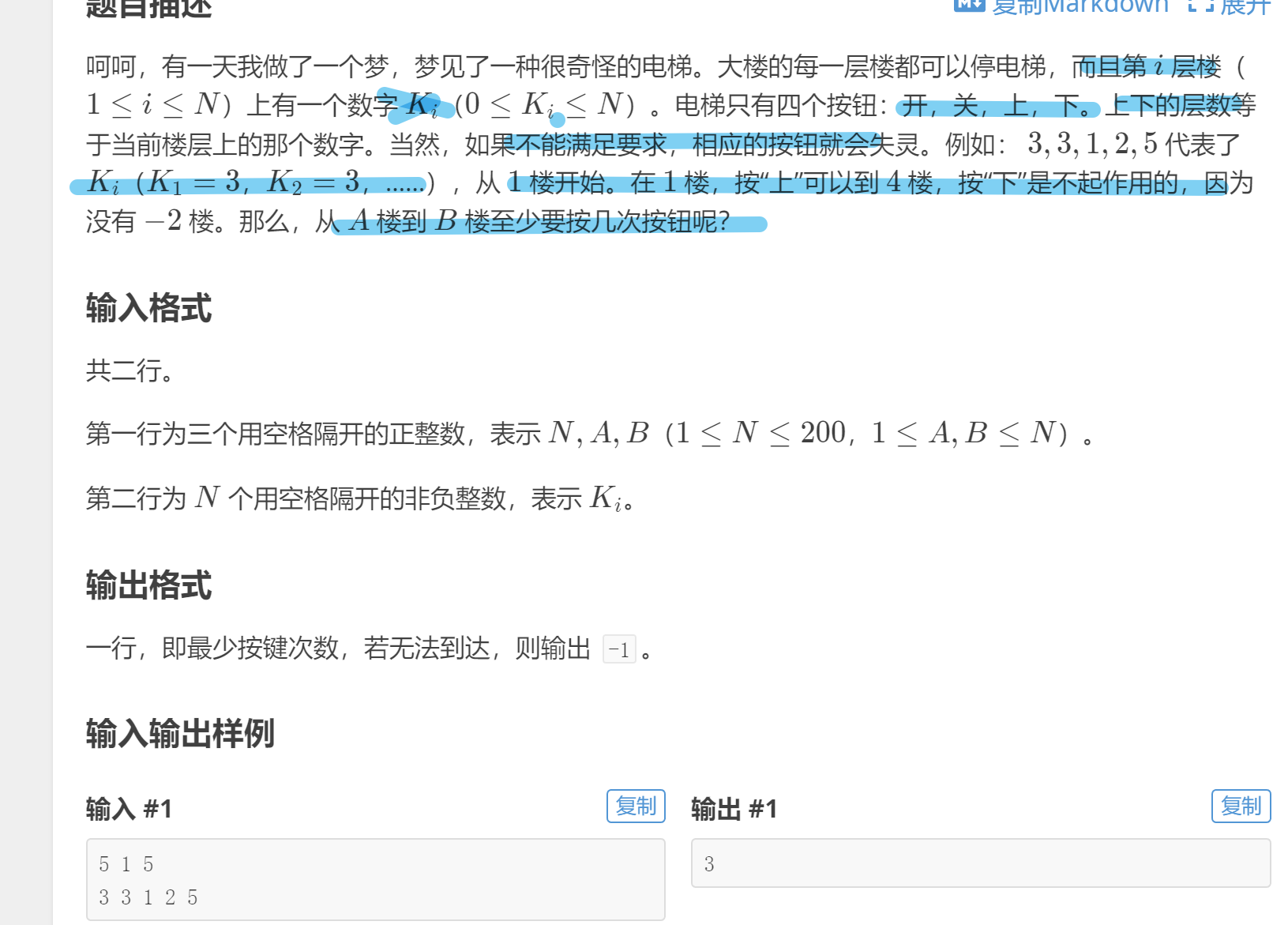
Ki 的值 表示 上 or 下 的层数
- 学个思路就可以
P1036 [NOIP2002 普及组] 选数 (组合)
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 30;int n, k;
int a[N], q[N];
int res = 0;//判断是否为素数
bool is_prime(int x) {if(x < 2) return false;for(int i = 2; i <= x / i; i ++) { // 从2开始呀if(x % i == 0) return false; }return true;
}void dfs(int x, int start) {if(x > k) {int sum = 0;for(int i = 1; i <= k; i ++) {sum += a[i];} if(is_prime(sum)) {res ++;}return;}for(int i = start; i <= n; i ++) {a[x] = q[i];dfs(x + 1, i + 1);a[x] = 0;}
}int main () {cin >> n >> k;for (int i = 1; i <= n; i ++ ) cin >> q[i];dfs(1, 1);cout << res << endl;return 0;
}
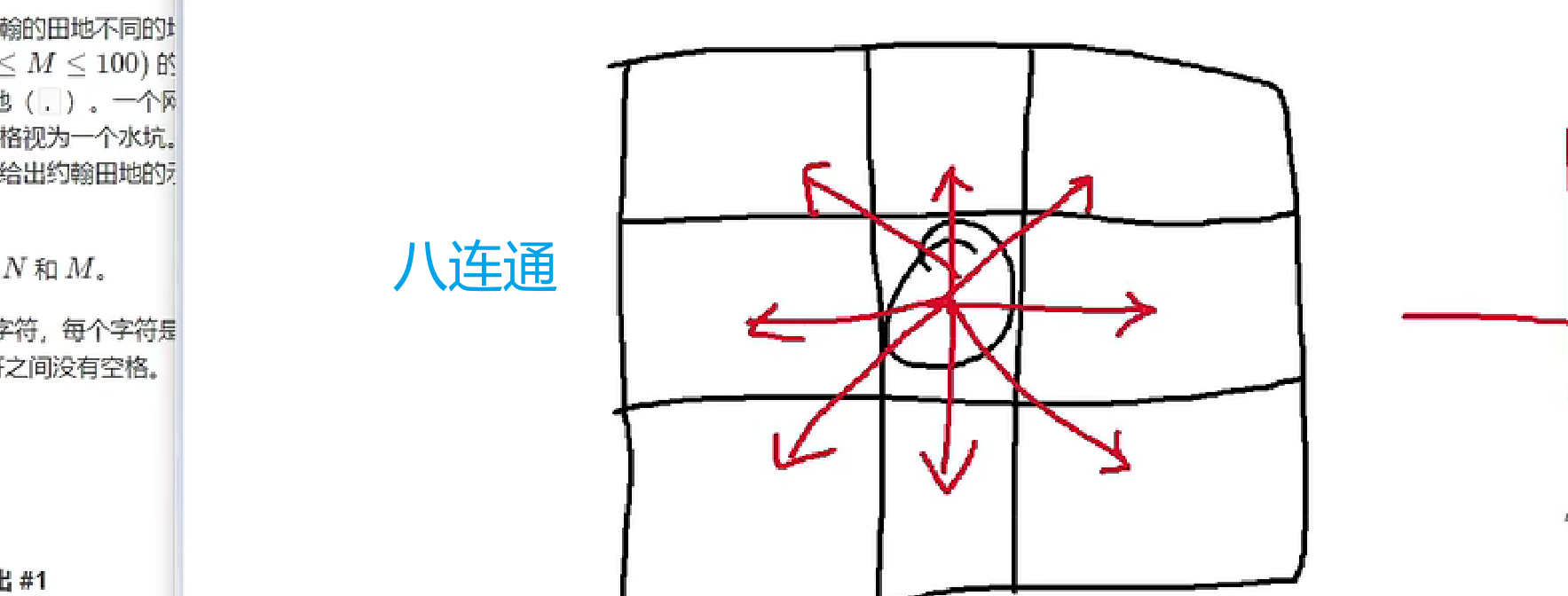
P1596 [USACO10OCT]Lake Counting S 【DFS求图的连通块】
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;int n, m;
char g[N][N];
bool st[N][N];
int res = 0;int dx[8] = {1,1,1,0,0,-1,-1,-1};
int dy[8] = {-1,0,1,1,-1,1,0,-1};void dfs(int x, int y) {for(int i = 0; i < 8; i ++) {int a = x + dx[i], b = y + dy[i];if(a < 0 || a >= n || b < 0 || b >= m) continue; // 越界if(g[a][b] != 'W' ) continue; // 不是山if(st[a][b]) continue; //来过st[a][b] = true;dfs(a, b);}
}int main () {cin >> n >> m;for(int i = 0; i < n; i ++) cin >> g[i];for (int i = 0; i < n; i ++ ) {for (int j = 0; j < m; j ++ ) {if(g[i][j] == 'W' && !st[i][j]) {dfs(i, j);res ++;}// cout << g[i][j] << ' ';}// cout << endl;}cout << res << endl;return 0;
}
八数码
- https://www.acwing.com/problem/content/1116/ 棋盘题
tijie : https://www.acwing.com/solution/content/133704/

相关文章:

【DFS专题】深度优先搜索 “暴搜”优质题单推荐 10道题(C++ | 洛谷 | acwing)
文章目录题单一、模板 [极为重要]全排列DFS组合型DFS指数DFS二、专题烤鸡 (指数BFS)P1088 火星人 【全排列】P1149 火彩棒 [预处理 ]P2036 PERKETP1135 奇怪的电梯 暴力P1036 [NOIP2002 普及组] 选数 (组合)P1596 [USACO10OCT]Lake Counting …...

微信小程序自定义组件生命周期有哪些?
微信小程序自定义组件的生命周期函数分为三类: 创建时执行的生命周期函数、更新时执行的生命周期函数和销毁时执行的生命周期函数。 下面是具体的生命周期函数及其触发时机: 创建时执行的生命周期函数: created:在组件实例刚刚…...
Linux就该这么学(六)
一、从“/”开始 Linux 系统中的文件和目录名称是严格区分大小写的。例如,root、rOOt、rooT 均代表不同的目录,并且文件名称中不得包含斜杠(/)。Linux 系统中的文件存储结构如下图所示。 在 Linux 系统中,最常见的目录…...
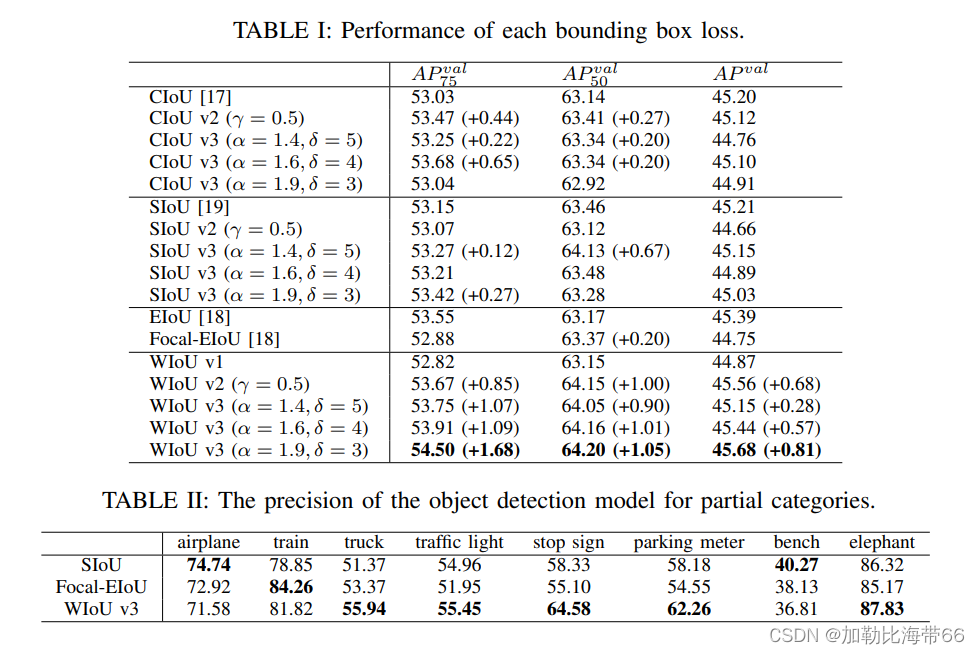
目标检测算法——YOLOv5/v7/v8改进结合涨点Trick之Wise-IoU(超越CIOU/SIOU)
超越CIOU/SIOU | Wise-IoU助力YOLO强势涨点!!! 论文题目:Wise-IoU: Bounding Box Regression Loss with Dynamic Focusing Mechanism 论文链接:https://arxiv.org/abs/2301.10051 近年来的研究大多假设训练数据中的…...

【蓝桥杯选拔赛真题39】python输出数字组合 青少年组蓝桥杯python 选拔赛STEMA比赛真题解析
目录 python输出数字组合 一、题目要求 1、编程实现 2、输入输出...

网络安全工程师做什么?
网络安全很复杂。数字化转型、远程工作和不断变化的威胁形势需要不同的工具和不同的技能组合。 系统必须到位以保护端点、身份和无边界网络边界。负责处理这种复杂安全基础设施的工作角色是网络安全工程师。 简而言之,网络安全工程师是负责设计和实施组织安全系…...
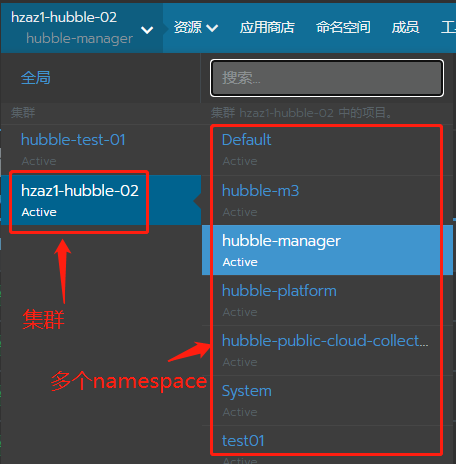
总结:K8S运维常用命令
一、部署./kubectl apply -f biz-healing-pod.yaml 二、查看部署的资源1、podkubectl get pod -A:获取所有pod没有IP?用-o wide参数看详细信息:./kubectl get pod -n deepflow -o wide2、service查看hubble-manager命名空间下有哪些service/d…...
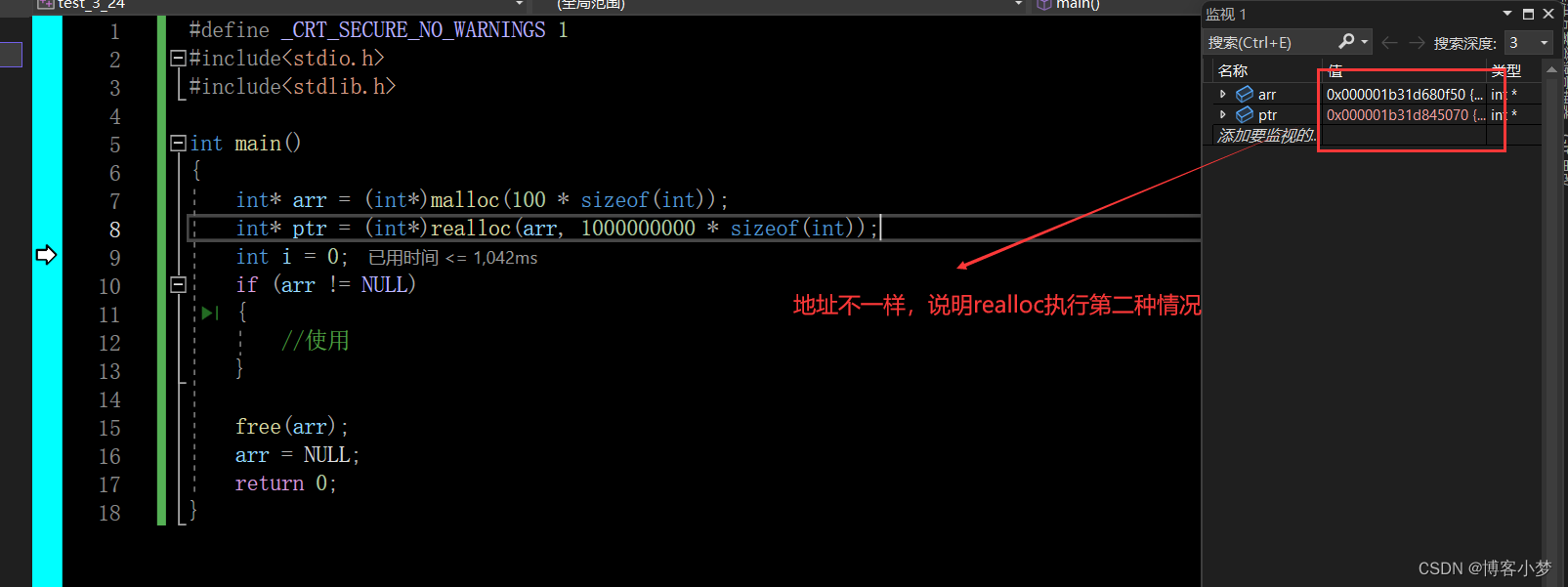
你是真的“C”——进行动态内存分配库函数的使用详解
你是真的“C”——申请动态空间库函数的使用详解😎前言🙌一、为什么需要动态内存分配?💞free 函数😘malloc 库函数😘calloc 库函数😘realloc 库函数😘总结撒花💞…...

Python|蓝桥杯进阶第五卷——数论
欢迎交流学习~~ 专栏: 蓝桥杯Python组刷题日寄 蓝桥杯进阶系列: 🏆 Python | 蓝桥杯进阶第一卷——字符串 🔎 Python | 蓝桥杯进阶第二卷——贪心 💝 Python | 蓝桥杯进阶第三卷——动态规划 ✈️ Python | 蓝桥杯进阶…...

用Python实现单例模式
什么是单例模式单例模式是指在内存中只会创建且仅创建一次对象的设计模式。在程序中多次使用同一个对象且作用相同时,为了防止频繁地创建对象使得内存飙升,单例模式可以让程序仅在内存中创建一个对象,让所有需要调用的地方都共享这一单例对象…...

交叉编译说明:工具链安装和环境变量配置
目录 一 简单了解交叉编译 ① 什么是交叉编译 ② 为什么需要交叉编译 ③ 宿主机和目标机 二 搭建交叉编译工作环境 ① 安装工具链 ② 配置环境变量 ● 配置临时环境变量 ● 配置永久环境变量 三 交叉编译宿主机和目标机 ● 宿主机编译生成的可执行文件下载到目…...
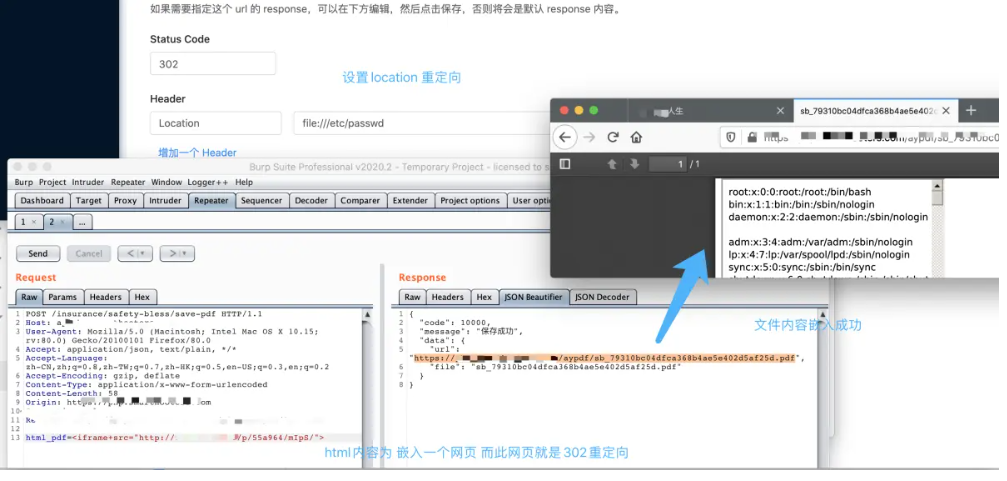
文件上传的多种利用方式
文件上传的多种利用方式 文件上传漏洞除了可以通过绕过检测进行webshell的上传之外,还有多种其它的漏洞可以进行测试。 XSS漏洞 文件名造成的XSS 当上传任何文件时,文件名肯定是会反显示在网页上,可以使用 XSS Payload做文件名尝试将其上传到…...
)
盘一盘C++的类型描述符(二)
先序文章请看 盘一盘C的类型描述符(一) 稍微组合一下的复杂类型 数组指针类型的数组类型 数组的指针类型我们已经了解了,那么,以这种类型作为元素的数组类型怎么搞? using type int (*)[3]; // 元素类型是数组指针…...

慎投,Frontiers这本期刊显示on hold中
什么是“On Hold”? 该期刊因为质量问题正在被进行重新评估;在重新评估过程中,不会检索新发表的文章。该期刊因为质量问题正在被进行重新评估;在重新评估过程中,不会检索新发表的文章。根据选择标准,在最严…...
——ProgressBar(史上最全))
Winform控件开发(21)——ProgressBar(史上最全)
一、属性 1、Name 用于获取控件对象 2、Anchor 锚定控件对于父控件的位置 3、BackColor 背景色 4、ContextMenuStrip 关联的上下文菜单 5、Cursor 鼠标移动到控件上显示的光标 6、Dock 停靠在父控件的位置 7、Enabled 是否启动该控件,false时事件都不能触发 8、…...

校招失败后,在外包公司熬了 2 年终于进了字节跳动,竭尽全力....
其实两年前校招的时候就往字节投了一次简历,结果很明显凉了,随后这个理想就被暂时放下了,但是这个种子一直埋在心里这两年除了工作以外,也会坚持写博客,也因此结识了很多优秀的小伙伴,从他们身上学到了特别…...
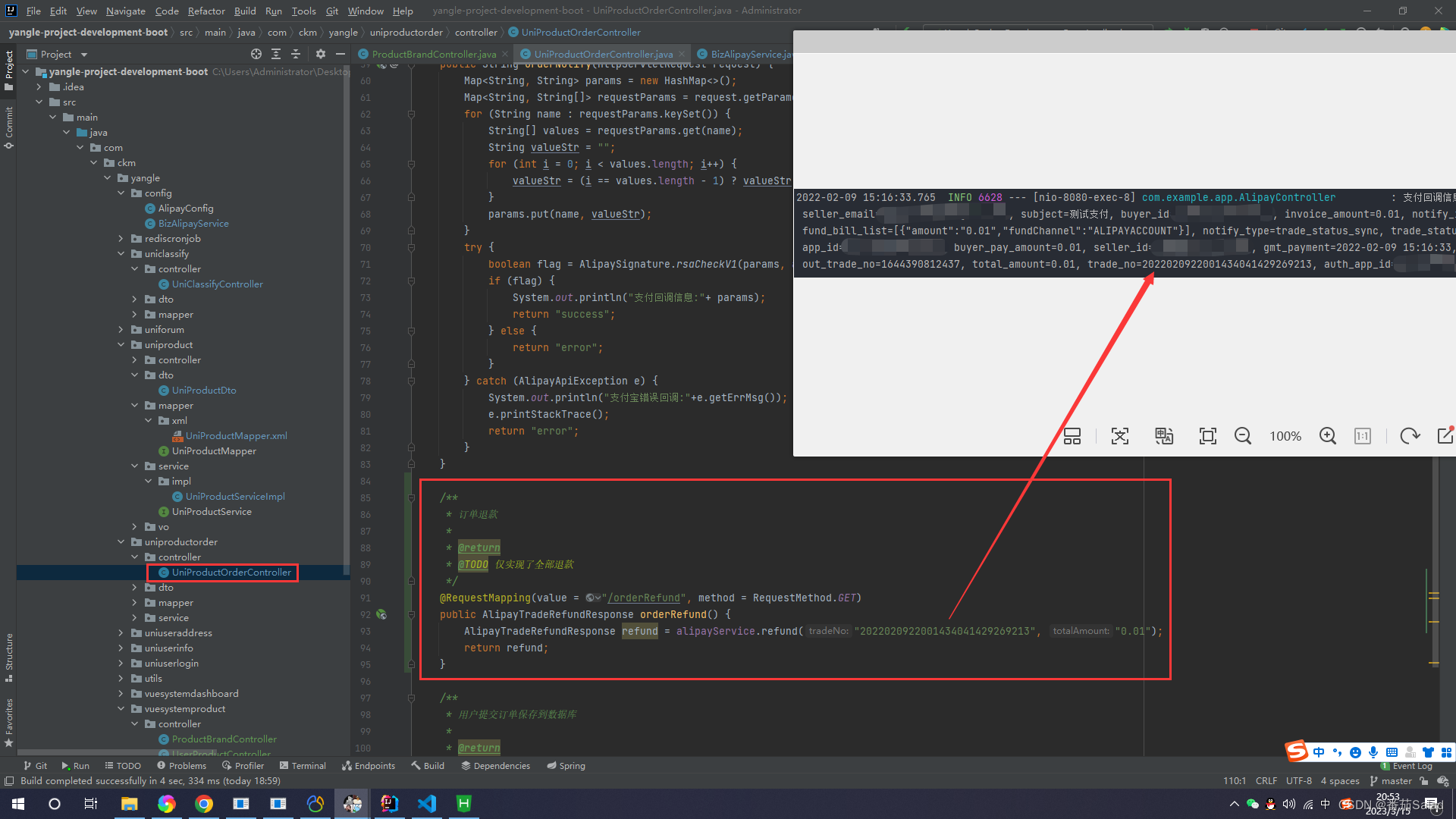
UniApp + SpringBoot 实现接入支付宝支付功能和退款功能
一、支付宝开放平台设置 注册支付宝支付功能需要个体工商户或企业才可以!需要有营业执照才能去申请哦! 1、登录到控制台 进入支付宝开放平台 控制台 2、开发设置 3、产品绑定APP支付 如果没有绑定APP支付就会报商家订单参数异常,请重新发起…...
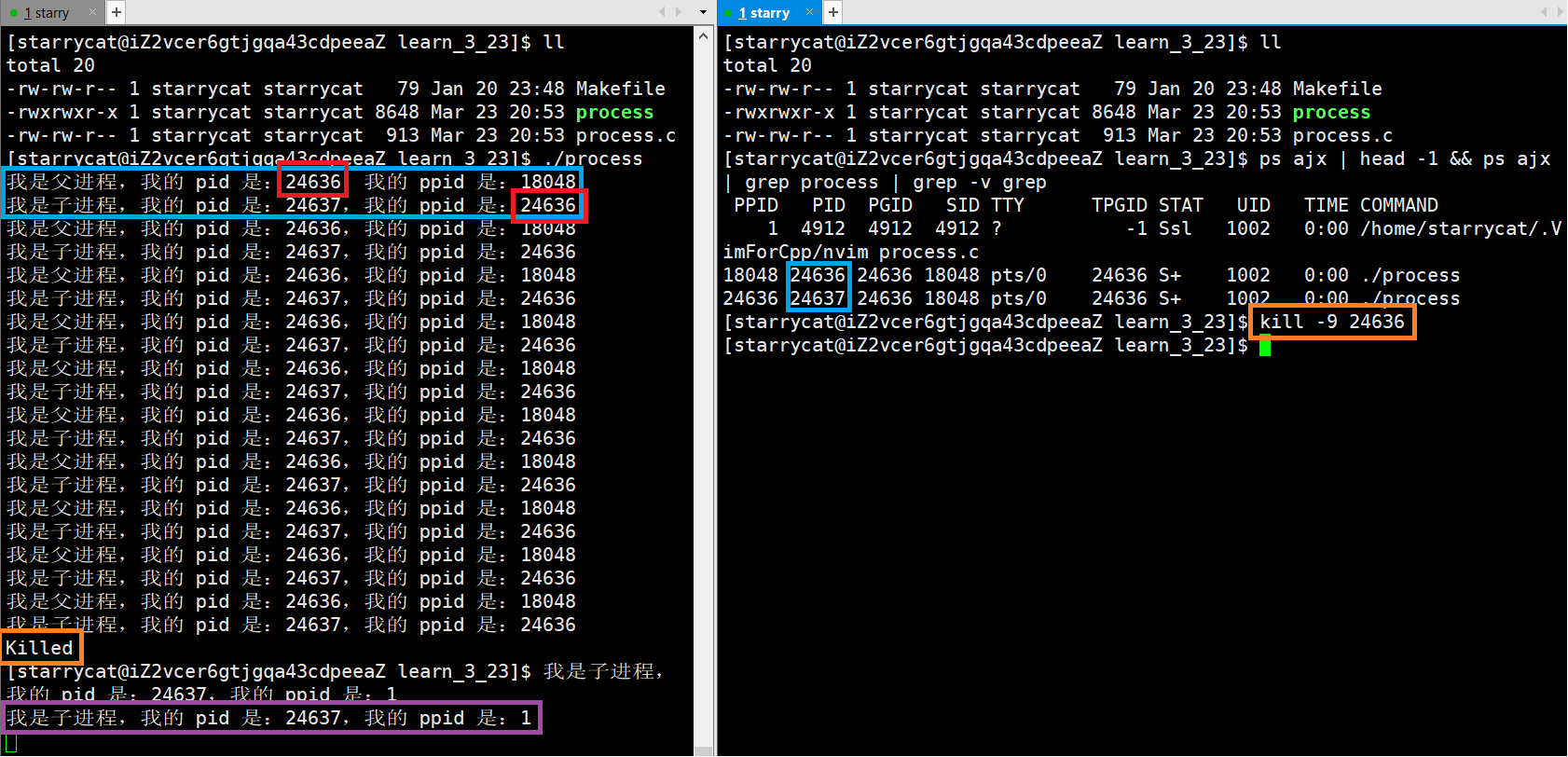
初识进程
文章目录一、进程的概念1. 进程是什么及进程的管理2. Linux 下的 pcb3. 系统调用接口 getpid 和 getppid4. 系统调用接口 fork一、进程的概念 1. 进程是什么及进程的管理 在 Linux下 ./binaryfile 运行一个程序或者在 Windows下双击运行一个程序时,程序就变成了一个…...
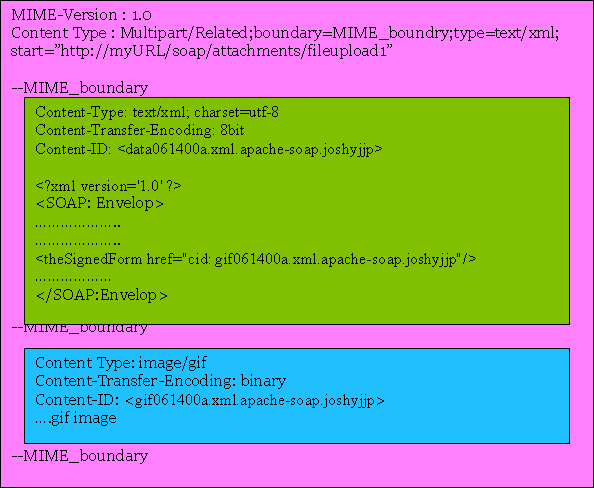
SOAP传输协议
一.HTTP传输协议 超文本传输协议(HyperText Transfer Protocol,缩写:HTTP),它是基于请求-响应的模式协议,客户端发出请求,服务器端给出响应并返回请求内容。方法如下,HTTP传输协议常…...
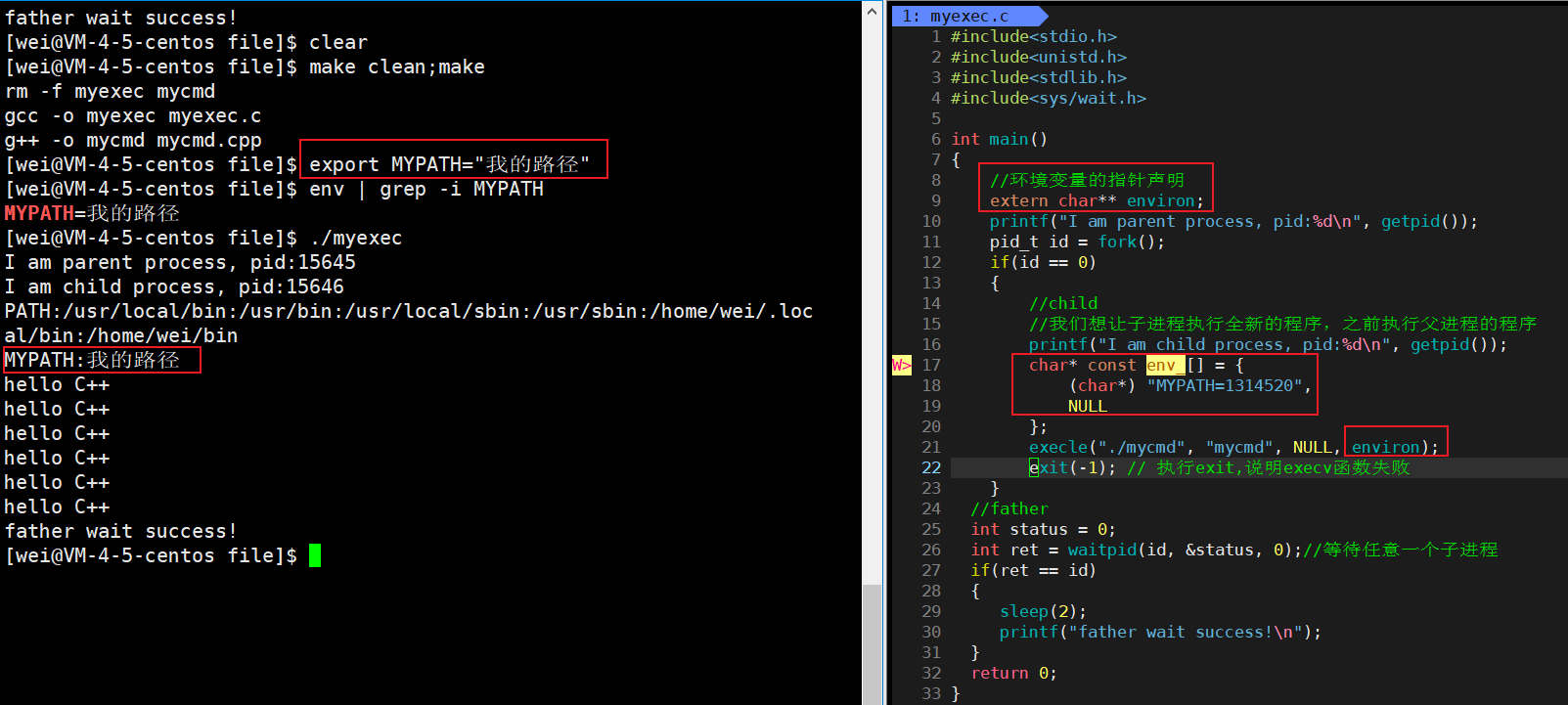
<Linux>进程控制
进程控制 文章目录进程控制一、进程创建1.fork函数认识2.写时拷贝3.fork常规用法4.fork调用失败的原因二、进程终止1.进程退出场景2.进程退出码3.进程退出的方式三、进程等待1.进程等待是什么?2.进程等待的必要性3.进程等待的方法3.1.wait函数3.2.waitpid函数4.如何…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...
