结营考试- 算法进阶营地 - DAY11

结营考试 - 算法进阶营地 - DAY11

• 测评链接；

A - 打卡题

考点：枚举；

分析

• 枚举 a _①_ b _②_ c = d，中两个运算符的 $3$ 种可能性，尝试寻找一种符合要求的答案。

参考代码

#include <bits/stdc++.h>
using namespace std;int a, b, c, d;
int solve(int u, int v, int flag)
{if (flag == 1)return u + v;else if (flag == 2)return u - v;else if (flag == 3)return u * v;
}int main()
{cin >> a >> b >> c >> d;for (int i = 1; i <= 3; i++)for (int j = 1; j <= 3; j++)if (solve(solve(a, b, i), c, j) == d){cout << "Yes" << endl;exit(0);}cout << "No" << endl;// system("pause");sreturn 0;
}

B - 溢出处理

分析

题目大意

新型病毒 91-DIVOC 正在广泛传播。

第一天有 $a$ 个人被感染，在接下来的每天中，每个感染者都会传染给另外的 $q$ 个人。定义传染系数为每天被感染的的人数的乘积，求 $k$ 天内的传染系数 对 722733748 取模 的结果。

题目分析

根据题意：

• 第一天有 $a$ 个人被感染。
• 在第二天时，这 $a$ 个人中每个人都会传染给另外的 $q$ 个人，因此第二天就有了 $a\times q$ 个人被感染。
• 第三天时，这 $a\times q$ 个人中每个人又会传染给另外的 $q$ 个人，因此第三天就有 $a\times q\times q$ 个人被感染。

以此类推，我们可以发现到第 k 天时，被感染的人数为 $a\times \underset{k-1}{\underbrace{q\times \cdots \times q}}$ 。

​ 求出了每天被感染的人数，只需要将它们乘起来就可以得到 $k$ 天内的传染系数。由于答案可能很大，因此我们需要边乘边取模。

参考代码

#include <bits/stdc++.h>
using namespace std;#define ll long long
const int mod = 722733748;
int k, a, q;
ll ans = 1, pre; // pre 前一项int main()
{cin >> k >> a >> q;pre = a;for (int i = 1; i <= k; i++){ans = (ans * pre) % mod;pre = (pre * q) % mod;}cout << ans << endl;// system("pause");return 0;
}

C - 进制、推理

考点：进制、贪心；

题意：

​ $T$ 组数据，每组数据给定两个数 $n$ 和 $m$，可以将 $n$ 和其他任何数进行与操作和或操作，问至少要进行多少次操作才能使 $n=m$。

分析

30分

• 爆搜。

正解

考虑将 $n$ 和 $m$ 都变成二进制数。

接下来，逐位比较 $n$ 和 $m$。

如果有一位上 $n$ 是 $1$，而 $m$ 是 $0$，就说明需要进行与操作，把 $n$ 的这一位变成 $0$。

同样，如果有一位 $n$ 是 $0$，而 $m$ 是 $1$，就说明需要进行或操作，把 $n$ 的这一位变成 $1$。

并且，同种操作可以同时完成。

所以，我们可以用两个布尔数组记录有没有出现以上两种情况。可证明，任意数据下，答案都 $\le 2$。

参考代码

#include <bits/stdc++.h>
using namespace std;#define ll long long
bool f1, f2;
ll T, a, b;int main()
{cin >> T;while (T--){cin >> a >> b;f1 = false, f2 = false;for (ll i = 2; i <= max(a, b) * 2; i <<= 1){ll x = a % i;ll y = b % i;if (x > y)f1 = true;if (x < y)f2 = true;}cout << f1 + f2 << endl;}// system("pause");return 0;
}

D - 贪心

考点：贪心、策略；

分析

题目大意

$n$ 个牛棚，编号为 $1\sim n$。初始时防御值分别为 $a_1,a_2,\cdots ,a_n$。有 $t$ 份补给，每份每份补给可以为某一个牛棚提供额外的 $1$ 点防御值。一个牛棚可以接受多份补给。

补给完成后，有 $m$ 块陨石分别撞击 $x_1,x_2,\cdots ,x_n$ 号牛棚，每次撞击会令对应牛棚防御值减少 2 点。当一间牛棚的防御值 $\le 0$ 时，牛棚会被破坏。

目前想要让被破坏的牛棚尽可能少。求在最优的补给策略下，被破坏的牛棚的最少的数量。

题目分析

不妨换一个角度来考虑。我们先让陨石撞击牛棚，计算出撞击后的牛棚的原始防御值，之后计算需要多少补给才能让某个牛棚不被破坏。即，我们计算每个牛棚的 $a_i-d_i$，并与 $1$（$1$ 是牛棚不被破坏的最少防御值）做比较。其中 $d_i$ 代表每个牛棚因陨石而损失的防御值。

在计算时，可以直接枚举陨石，并直接在 $a$ 数组中做操作。核心代码如下：

for (int i = 1; i <= m; ++i) {int x;cin >> x;a[x] -= 2;
}

可以很显然地考虑到，当 $a_i-d_i<1$ 时，我们需要补给这个牛棚，补给的数量是 $1-(a_i-d_i)$。在补给有限的情况下，如果想要让尽可能多的牛棚存活，那显然需要优先补给 $1-(a_i-d_i)$ 更小的牛棚。

因此，可以使用冒泡排序等方法，将 $1-(a_i-d_i)$ 由小到大排序（或将 $(a_i-d_i)$ 由大到小排序也可，核心思路是一致的）。

for (int i = 1; i <= n; ++i) {a[i] = 1 - a[i]; // 此处 a[i] 已经减去了损失值，直接覆写// 代表需要的补给数量
}// 冒泡排序
for (int i = 1; i <= n; ++i) {for (int j = 1; j < n; ++j) {if (a[j] > a[j + 1])swap(a[j], a[j + 1]);}
}

排序后，开始分配补给。从前往后枚举 $i$ ，判断每个牛棚的 $1-(a_i-d_i)$ 是否大于 $0$（即需要补给）。如果小于等于 $0$，代表不需要补给，直接跳过；如果大于 $0$，判断当前剩余的补给是否够填补上 $1-(a_i-d_i)$，如果足够则直接减去，否则中止补给。

在过程中，遇到「不需要补给」和「补给成功」的牛棚，同时计数即可。

int ans = 0;
for (int i = 1; i <= n; ++i) {// a[i] 代表需要的补给数量，上方已经覆写if (a[i] <= 0) { // 不需要补给ans++;} else {if (t >= a[i]) { // 剩余的 t 足够补给该牛棚t -= a[i]; // 减去补给该牛棚的消耗ans++;} else break; // 否则直接中断循环，因为后面的补给量只会越来越大，一定无法补给成功}
}
cout << ans << endl;

参考代码

#include <bits/stdc++.h>
using namespace std;const int N = 5e3 + 10;
int T, n, m, t;
int a[N];int main()
{cin >> T;while (T--){cin >> n >> t >> m;for (int i = 1; i <= n; i++)cin >> a[i];// 反过来先处理损失被砸下去后总修复的能量值for (int i = 1, x; i <= m; i++)cin >> x, a[x] -= 2;for (int i = 1; i <= n; i++)// 距离补给 1 防御值最近的牛棚做数值处理a[i] = 1 - a[i];int ans = 0;// 将需要修复的能量值 “贪心” 的从小到大排序，优先修复值小的牛棚sort(a + 1, a + 1 + n);for (int i = 1; i <= n; i++){if (a[i] <= 0)ans++; // 不需要补给else       // 补给{if (t >= a[i]) // 还够时间补给{t -= a[i];ans++;}else // 不够时间补给，则退出break;}}cout << ans << endl;}// system("pause");return 0;
}

E - 数学、找规律

考点：数学、枚举；

分析

题目大意

小 A 的地图可看作是一个 $n$ 行 $m$ 列的表格，其中每个格子可以看作一个城市。可是，地图上每个城市的粮食数不是它本身的粮食数，而是它与它相邻的所有的城市的粮食数之和。求所有城市的实际粮食数之和。（保证 $n,m$ 均为 $3$ 的倍数）

题目分析

因为每个城市在小 A 地图上的粮食数都是它与它相邻的所有的城市的粮食数之和，所以我们可以通过它得到它所在的 $3\times 3$ 矩阵的实际粮食数。

又因为数据保证 $n,m$ 均为 $3$ 的倍数，所以我们可以将地图分割为若干个 $3\times 3$ 矩阵。

故枚举所有在 $3\times 3$ 矩阵的中心的城市并将其在地图上显示的粮食数相加即可得到实际粮食数的总和。

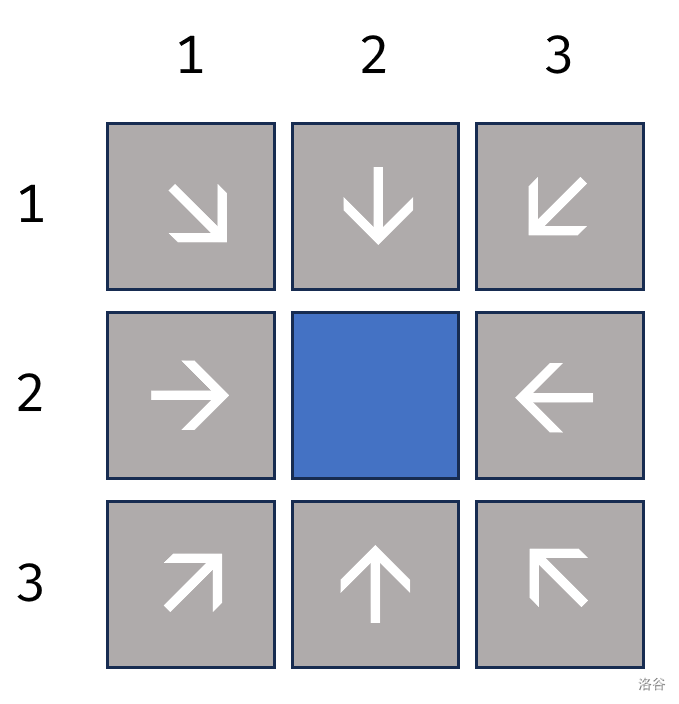
核心代码

for(int i=2;i<=n;i+=3){for(int j=2;j<=m;j+=3){sum+=a[i][j];}
}

[!WARNING]

最多 $110$ 个 $9\ast 9$ 方格，$110\ast 10^9=1.1\ast 10^{11}$ 会超出 int 类型范围，sum 要开 long long。

参考代码

#include <bits/stdc++.h>
using namespace std;#define ll long long
const int N = 1001;
int n, m;
int a[N][N];
ll sum;int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> a[i][j];for (int i = 2; i <= n; i += 3)for (int j = 2; j <= m; j += 3)sum += a[i][j];cout << sum << endl;// system("pause");return 0;
}

F - DP / 记忆化搜索

考点：记忆化搜索 / DP；

分析

题意：略过。1

[!WARNING]

• 最开始站在树 $1$。

状态分析：

• $dp[i][j]$：表示奶牛在第 $i$ 分钟内转移了 $j$ 次能够接到的最多苹果。

那么显而易见，对于每一分钟来说，枚举转移次数从而得到解

• $dp[i][j]=max(dp[i-1][j],dp[i-1][j-1])$，要么上一时刻$(t-1)$，移动 / 不移动。

• 同时如果 $a[i]=j\%2+1$ ，奶牛一开始在树 $1$，移动次数 如果为奇数时候一定在树 $2$，偶数次数的时候一定在树 $1$，注意要让次数加一。

初始化是数组一开始都是 $0$。

最终的答案是到第 $T$ 分钟时奶牛走 $1\sim w$ 步能够取得的最多苹果。

参考代码

#include <bits/stdc++.h>
using namespace std;const int N = 1005, M = 35;
int n, m;
int f[N][M], a[N], ans;int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> a[i];                           // 第 i 时刻，所在树的编号for (int i = 1; i <= n; i++)               // 枚举时间for (int j = 0; j <= n && j <= m; j++) // 移动的次数{if (j == 0) // 没有移动次数，直接继承f[i][j] = f[i - 1][j];elsef[i][j] = max(f[i - 1][j], f[i - 1][j - 1]); // 不移动、移动if (a[i] == j % 2 + 1)                           // 一开始站在树 1，移动次数如果为奇数时候一定在树 2，偶数次数的时候一定在树 1，二者不能同时被修改f[i][j]++;}// 在 0 ~ n 时刻下找答案for (int i = 0; i <= m; i++)ans = max(ans, f[n][i]);cout << ans << endl;// system("pause");return 0;
}

G - DP / topo

考点：DP、topo；

分析

为什么要拓扑排序？

小杨有个包含 $n$ 个节点 $m$ 条边的有向无环图。
根据路径上的经过节点的先后顺序可以得到一个节点权值的序列。

DP 开始

定义

第一种

直接套，$fi$ 表示从某个点到点 $i$，最长不下降子序列的最大长度。然后每遇到一条边就更新一次。

时间复杂度：一共 $m$ 条边，每条边转移时间复杂度为 $O(n)$，总时间复杂度为 $O(nm)$，毫无疑问会 TLE。看来不行。

第二种

抓住题目的“弱点”，发现一个很奇怪的条件，$1\le Ai\le 10$，也就是点权大小不超过 $10$。

所以可以成为 $f$ 的第二维：

$f_{i,j}$ 代表从某个点开始，到点 $i$，满足最后一个数字为 $j$ 的最长不下降子序列的最大长度。

初始状态

所有 $f_{i,A_i}=1$：只有当前点。

转移顺序

拓扑序，如果不是，在转移当前点时可能某个前驱节点还没转移到，如果从那个节点转移到这个节点刚好是最优解（或者最优解的一部分），答案就会出错。

状态转移方程

重点来了！

对于点 $v$ 的某一个前驱结点 $u$（或者对于点 $u$ 的某个后继结点 $v$），有两种转移：

第一种

一种是将点 $v$ 加入到点 $u$ 的最长不下降子序列中，比如：

此时点 $u$ 的最长不下降子序列为 $1,2,3$（即 $f_{u,3}=3$），而 $A_v\ge 3$，则这种转移会使 $f_{v,Av}=f_{u,3}+1=4$，前提是原 $f_{v,Av}<4$（不然得到更劣的解）。

不难知道：
$$\forall 1\le i\le A_v:f_v,A_i=max(f_{v,A_i},f_{u,i+1});$$
右边很好理解。左边为什么是 $1\le i\le A_v$ 呢？不可以大于 $A_v$ 吗？

不可以。

因为在 不下降序列的末尾 增加一个 比原来的末尾更小的元素，增加后就 不是不下降序列了。

比如你在不下降序列 1,2,3 最后加入一个 2，最后还满足不下降吗？显然不满足。

第二种

第二种就是不算上元素 $v$，本来是 1,2,3 现在还是 1,2,3，子序列嘛，可以去除某些元素（这里是去除元素 $v$）。

$\forall 1\le i\le 10:f_{v,i}=max(f_{v,i},f_{u,i})$

答案

所有有意义的 $f_{i,j}$ 的最大值（有意义：$1\le i\le n，1\le j\le 10$）；

参考代码

#include <bits/stdc++.h>
using namespace std;const int N = 1e5 + 10;
vector<int> e[N];
int n, m, w[N], ind[N];
int f[N][12]; // f[i][j]：表示到达点 i 最后一个数字为 j 的最长不下降子序列长度
queue<int> q;void topo()
{for (int i = 1; i <= n; i++){if (ind[i] == 0)q.push(i);f[i][w[i]] = 1; // 到达点 i 用时为 w[i] 的长度至少为本身 1}while (q.size()){int u = q.front();q.pop();for (auto v : e[u]){if (--ind[v] == 0) // 松弛q.push(v);// 转移1：枚举 u 点到达 v 点的上一个状态， f[u][j], 1 <= j <= w[v]，是否加入 w[v] 后会更长for (int j = 1; j <= w[v]; j++)f[v][w[v]] = max(f[v][w[v]], f[u][j] + 1);// 转移2：不加上当前点 v 的点权会更优的情况for (int j = 1; j <= 10; j++)f[v][j] = max(f[v][j], f[u][j]);}}
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++)cin >> w[i];for (int i = 1, u, v; i <= m; i++){cin >> u >> v;e[u].push_back(v); // 加边ind[v]++;}// topotopo();// 在 n 个点 1~10 的点权上找最大不下降子序列长度int res = 0;for (int i = 1; i <= n; i++)for (int j = 1; j <= 10; j++)res = max(res, f[i][j]);cout << res << endl;// system("pause");return 0;
}

H - 贪心、位运算

考点：贪心、位运算；

分析

显然的，答案在二进制下的第 $i$ 位为 $1$ 一定比该位为 $0$ 更优。

故贪心的策略：考虑 从高到低枚举答案 的二进制位，若该位可取 1 则必定贪心取 1（优先取位权大的），而根据这个结果再去检查后面更低位能否取。

下面问题在于如何检验第 $i$ 位是否可行。由于只能合并相邻两项，故合并 $k$ 次相当于将原序列分为 $n-k$ 段，每一段内按位或。因此，考虑用 $p$ 维护当前段内的按位或值，若某一时刻 $p$ 二进制下第 $i$ 位为 1，且与已得出的更高位部分的答案不矛盾，则可以贪心的开启新的一段。最后仅需判断段数是否不小于 $n-k$ 即可。

时间复杂度 $O(nlogV)$。

参考代码

#include <bits/stdc++.h>
using namespace std;#define ll long longconst int N = 2e5 + 10, V = 30;
int n, k, a[N], ans;bool check(int d)
{int res = 0, p = 0;for (int i = 1; i <= n + 1; i++){p |= a[i];        // 或 1~n+1if ((p & d) == d) // 当前数 a[i] 与目标 d 位相同，则另起一段新的合并序列res++, p = 0;}return res >= k; // true 尝试更小的 d 是否也可以行
}int main()
{cin >> n >> k;k = n - k; // 合并的次数for (int i = 1; i <= n; i++)cin >> a[i];for (int i = V; i >= 0; i--) // 从高位到低位枚举 “贪心的策略” 使得结果尽可能大if (check(ans + (1 << i)))ans += (1 << i);cout << ans << endl;// system("pause");return 0;
}