【机器学习】CNN的数学基础


🌈个人主页: 鑫宝Code
🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础
💫个人格言: "如无必要,勿增实体"

文章目录
- CNN的数学基础
- 1. 引言
- 2. 卷积运算
- 2.1 连续卷积
- 2.2 离散卷积
- 2.3 互相关
- 3. 激活函数
- 3.1 ReLU (Rectified Linear Unit)
- 3.2 Sigmoid
- 3.3 Tanh
- 4. 池化操作
- 4.1 最大池化
- 4.2 平均池化
- 5. 损失函数
- 5.1 均方误差(MSE)
- 5.2 交叉熵
- 6. 反向传播算法
- 6.1 链式法则
- 6.2 卷积层的反向传播
- 6.3 池化层的反向传播
- 7. 优化算法
- 7.1 随机梯度下降(SGD)
- 7.2 动量法
- 7.3 Adam
- 8. 正则化技术
- 8.1 L2正则化
- 8.2 Dropout
- 9. 初始化方法
- 9.1 Xavier初始化
- 9.2 He初始化
- 10. 结论
CNN的数学基础
1. 引言
卷积神经网络(Convolutional Neural Network,CNN)作为深度学习中的重要模型,其强大性能背后蕴含着丰富的数学原理。本文将深入探讨CNN的数学基础,包括卷积运算、激活函数、池化操作、反向传播算法以及优化方法等核心概念。通过对这些数学基础的理解,我们可以更好地把握CNN的本质,为进一步优化和创新CNN模型奠定基础。

2. 卷积运算
2.1 连续卷积
在数学中,连续函数的卷积定义如下:
( f ∗ g ) ( t ) = ∫ − ∞ ∞ f ( τ ) g ( t − τ ) d τ (f * g)(t) = \int_{-\infty}^{\infty} f(\tau)g(t-\tau)d\tau (f∗g)(t)=∫−∞∞f(τ)g(t−τ)dτ
其中, f f f和 g g g是两个可积函数, ∗ * ∗表示卷积操作。
2.2 离散卷积
在CNN中,我们主要关注离散卷积。对于二维离散卷积,其定义为:
( I ∗ K ) ( i , j ) = ∑ m ∑ n I ( m , n ) K ( i − m , j − n ) (I * K)(i,j) = \sum_{m}\sum_{n} I(m,n)K(i-m,j-n) (I∗K)(i,j)=m∑n∑I(m,n)K(i−m,j−n)
其中, I I I是输入(如图像), K K K是卷积核(或称滤波器)。
2.3 互相关
实际上,CNN中使用的"卷积"操作更准确地说是互相关(cross-correlation):
( I ⋆ K ) ( i , j ) = ∑ m ∑ n I ( i + m , j + n ) K ( m , n ) (I \star K)(i,j) = \sum_{m}\sum_{n} I(i+m,j+n)K(m,n) (I⋆K)(i,j)=m∑n∑I(i+m,j+n)K(m,n)
这里 ⋆ \star ⋆表示互相关操作。与真正的卷积相比,互相关不需要将卷积核翻转。

3. 激活函数
激活函数为神经网络引入非线性,增强模型的表达能力。
3.1 ReLU (Rectified Linear Unit)
ReLU是目前最常用的激活函数之一:
f ( x ) = max ( 0 , x ) f(x) = \max(0, x) f(x)=max(0,x)
其导数为:
f ′ ( x ) = { 1 , if x > 0 0 , if x ≤ 0 f'(x) = \begin{cases} 1, & \text{if } x > 0 \\ 0, & \text{if } x \leq 0 \end{cases} f′(x)={1,0,if x>0if x≤0
3.2 Sigmoid
Sigmoid函数将输入映射到(0, 1)区间:
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1 + e^{-x}} σ(x)=1+e−x1
其导数为:
σ ′ ( x ) = σ ( x ) ( 1 − σ ( x ) ) \sigma'(x) = \sigma(x)(1 - \sigma(x)) σ′(x)=σ(x)(1−σ(x))
3.3 Tanh
Tanh函数将输入映射到(-1, 1)区间:
tanh ( x ) = e x − e − x e x + e − x \tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} tanh(x)=ex+e−xex−e−x
其导数为:
tanh ′ ( x ) = 1 − tanh 2 ( x ) \tanh'(x) = 1 - \tanh^2(x) tanh′(x)=1−tanh2(x)
4. 池化操作
池化操作用于降低特征图的空间分辨率,减少参数数量和计算量。
4.1 最大池化
最大池化选择池化窗口内的最大值:
y i j = max ( m , n ) ∈ R i j x m n y_{ij} = \max_{(m,n) \in R_{ij}} x_{mn} yij=(m,n)∈Rijmaxxmn
其中, R i j R_{ij} Rij是以 ( i , j ) (i,j) (i,j)为中心的池化窗口。
4.2 平均池化
平均池化计算池化窗口内的平均值:
y i j = 1 ∣ R i j ∣ ∑ ( m , n ) ∈ R i j x m n y_{ij} = \frac{1}{|R_{ij}|} \sum_{(m,n) \in R_{ij}} x_{mn} yij=∣Rij∣1(m,n)∈Rij∑xmn

5. 损失函数
损失函数衡量模型预测与真实标签之间的差距。
5.1 均方误差(MSE)
对于回归问题,常用均方误差:
L M S E = 1 N ∑ i = 1 N ( y i − y ^ i ) 2 L_{MSE} = \frac{1}{N} \sum_{i=1}^N (y_i - \hat{y}_i)^2 LMSE=N1i=1∑N(yi−y^i)2
其中, y i y_i yi是真实值, y ^ i \hat{y}_i y^i是预测值, N N N是样本数量。
5.2 交叉熵
对于分类问题,常用交叉熵损失:
L C E = − ∑ i = 1 C y i log ( y ^ i ) L_{CE} = -\sum_{i=1}^C y_i \log(\hat{y}_i) LCE=−i=1∑Cyilog(y^i)
其中, C C C是类别数, y i y_i yi是真实标签(one-hot编码), y ^ i \hat{y}_i y^i是预测概率。
6. 反向传播算法
反向传播是训练神经网络的核心算法,用于计算损失函数对各层参数的梯度。
6.1 链式法则
反向传播基于链式法则:
∂ L ∂ w = ∂ L ∂ y ⋅ ∂ y ∂ x ⋅ ∂ x ∂ w \frac{\partial L}{\partial w} = \frac{\partial L}{\partial y} \cdot \frac{\partial y}{\partial x} \cdot \frac{\partial x}{\partial w} ∂w∂L=∂y∂L⋅∂x∂y⋅∂w∂x
其中, L L L是损失函数, w w w是待优化的参数。
6.2 卷积层的反向传播
对于卷积层,我们需要计算损失函数对卷积核权重的梯度:
∂ L ∂ K = ∑ i , j ∂ L ∂ Y i j ⋅ X i j \frac{\partial L}{\partial K} = \sum_{i,j} \frac{\partial L}{\partial Y_{ij}} \cdot X_{ij} ∂K∂L=i,j∑∂Yij∂L⋅Xij
其中, K K K是卷积核, Y Y Y是输出特征图, X X X是输入特征图。
6.3 池化层的反向传播
对于最大池化,梯度只传递给池化窗口中的最大值元素:
∂ L ∂ x m n = { ∂ L ∂ y i j , if x m n = max ( m , n ) ∈ R i j x m n 0 , otherwise \frac{\partial L}{\partial x_{mn}} = \begin{cases} \frac{\partial L}{\partial y_{ij}}, & \text{if } x_{mn} = \max_{(m,n) \in R_{ij}} x_{mn} \\ 0, & \text{otherwise} \end{cases} ∂xmn∂L={∂yij∂L,0,if xmn=max(m,n)∈Rijxmnotherwise
对于平均池化,梯度平均分配给池化窗口内的所有元素:
∂ L ∂ x m n = 1 ∣ R i j ∣ ∂ L ∂ y i j \frac{\partial L}{\partial x_{mn}} = \frac{1}{|R_{ij}|} \frac{\partial L}{\partial y_{ij}} ∂xmn∂L=∣Rij∣1∂yij∂L
7. 优化算法
优化算法用于更新网络参数,最小化损失函数。
7.1 随机梯度下降(SGD)
最基本的优化算法是随机梯度下降:
w t + 1 = w t − η ∇ L ( w t ) w_{t+1} = w_t - \eta \nabla L(w_t) wt+1=wt−η∇L(wt)
其中, η \eta η是学习率, ∇ L ( w t ) \nabla L(w_t) ∇L(wt)是损失函数关于参数 w t w_t wt的梯度。
7.2 动量法
动量法引入了历史梯度信息,加速收敛:
v t + 1 = γ v t + η ∇ L ( w t ) w t + 1 = w t − v t + 1 \begin{aligned} v_{t+1} &= \gamma v_t + \eta \nabla L(w_t) \\ w_{t+1} &= w_t - v_{t+1} \end{aligned} vt+1wt+1=γvt+η∇L(wt)=wt−vt+1
其中, γ \gamma γ是动量系数。
7.3 Adam
Adam结合了动量法和自适应学习率:
m t = β 1 m t − 1 + ( 1 − β 1 ) ∇ L ( w t ) v t = β 2 v t − 1 + ( 1 − β 2 ) ( ∇ L ( w t ) ) 2 m ^ t = m t 1 − β 1 t v ^ t = v t 1 − β 2 t w t + 1 = w t − η v ^ t + ϵ m ^ t \begin{aligned} m_t &= \beta_1 m_{t-1} + (1-\beta_1) \nabla L(w_t) \\ v_t &= \beta_2 v_{t-1} + (1-\beta_2) (\nabla L(w_t))^2 \\ \hat{m}_t &= \frac{m_t}{1-\beta_1^t} \\ \hat{v}_t &= \frac{v_t}{1-\beta_2^t} \\ w_{t+1} &= w_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t \end{aligned} mtvtm^tv^twt+1=β1mt−1+(1−β1)∇L(wt)=β2vt−1+(1−β2)(∇L(wt))2=1−β1tmt=1−β2tvt=wt−v^t+ϵηm^t
其中, β 1 \beta_1 β1和 β 2 \beta_2 β2是衰减率, ϵ \epsilon ϵ是一个小常数。
8. 正则化技术
正则化用于防止过拟合,提高模型的泛化能力。
8.1 L2正则化
L2正则化在损失函数中添加参数的平方和:
L r e g = L + λ 2 ∑ w w 2 L_{reg} = L + \frac{\lambda}{2} \sum_w w^2 Lreg=L+2λw∑w2
其中, λ \lambda λ是正则化系数。
8.2 Dropout
Dropout随机丢弃一部分神经元,可以看作是集成学习的一种形式。在训练时:
y = f ( W x ) ⊙ m , m i ∼ Bernoulli ( p ) y = f(Wx) \odot m, \quad m_i \sim \text{Bernoulli}(p) y=f(Wx)⊙m,mi∼Bernoulli(p)
其中, ⊙ \odot ⊙表示元素wise乘法, m m m是一个二元掩码, p p p是保留神经元的概率。

9. 初始化方法
参数初始化对CNN的训练至关重要。
9.1 Xavier初始化
Xavier初始化适用于tanh激活函数:
W ∼ U ( − 6 n i n + n o u t , 6 n i n + n o u t ) W \sim U\left(-\sqrt{\frac{6}{n_{in} + n_{out}}}, \sqrt{\frac{6}{n_{in} + n_{out}}}\right) W∼U(−nin+nout6,nin+nout6)
其中, n i n n_{in} nin和 n o u t n_{out} nout分别是输入和输出的神经元数量。
9.2 He初始化
He初始化适用于ReLU激活函数:
W ∼ N ( 0 , 2 n i n ) W \sim N\left(0, \sqrt{\frac{2}{n_{in}}}\right) W∼N(0,nin2)
10. 结论
本文深入探讨了CNN的数学基础,包括卷积运算、激活函数、池化操作、反向传播算法、优化方法、正则化技术和初始化方法等核心概念。这些数学原理构成了CNN的理论基础,对于理解CNN的工作原理、改进现有模型和设计新的架构都至关重要。
随着深度学习的不断发展,CNN的数学理论也在不断完善和扩展。例如,群论在解释CNN的等变性方面发挥了重要作用,而信息论则为理解CNN的表示学习能力提供了新的视角。未来,结合更多数学分支的研究将有助于我们更深入地理解CNN,推动其在各个领域的应用和创新。


相关文章:

【机器学习】CNN的数学基础
🌈个人主页: 鑫宝Code 🔥热门专栏: 闲话杂谈| 炫酷HTML | JavaScript基础 💫个人格言: "如无必要,勿增实体" 文章目录 CNN的数学基础1. 引言2. 卷积运算2.1 连续卷积2.2 离散卷积2.3 互相关 3. 激活函…...

最小路径和[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个包含非负整数的m x n网格grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 说明:每次只能向下或者向右移动一步。 示例 1: 输入:grid [[…...

【题库】——数组 小鱼比可爱
#include<bits/stdc.h> using namespace std; int main() {int n,m,i;cin>>n;int arr[n]; for(i0;i<n;i) {int count 0;cin>>arr[i];for(mi;m>0;m--){if(arr[i]>arr[m])count;} cout<<count<<" "; } return 0; }...
基于飞腾平台的Hbase的安装配置
【写在前面】 飞腾开发者平台是基于飞腾自身强大的技术基础和开放能力,聚合行业内优秀资源而打造的。该平台覆盖了操作系统、算法、数据库、安全、平台工具、虚拟化、存储、网络、固件等多个前沿技术领域,包含了应用使能套件、软件仓库、软件支持、软件适…...

【springboot】springboot接口参数全局解密,解决request内容修改后如何重新设置回去的问题
文章目录 核心思路spring&servelt基础核心接口类核心代码 body解密核心原理讲解get解密核心原理讲解get query请求讲解get pathVariables请求讲解 总结 本文不仅介绍了body内容修改后如何传递,也介绍了get请求 在修改内容后如何继续传递。 【原创作者 csdn: 孟秋…...

yml基本语法
YAML(YAML Ain’t Markup Language)是一种简洁且易读的数据序列化格式,常用于配置文件。Spring Boot 中的 application.yml 文件使用 YAML 来配置应用程序的属性。 YAML 基本语法 1. 键值对 基本的键值对表示形式为:key: value…...
橙色简洁大气体育直播自适应模板赛事直播门户自适应网站源码
源码名称:酷黑简洁大气体育直播自适应模板赛事直播门户网站 源码开发环境:帝国cms 7.5 安装环境:phpmysql 带采集,可以挂着电脑上自动采集发布,无需人工操作! 橙色简洁大气体育直播自适应模板赛事直播门户…...

【启明智显技术分享】工业级HMI芯片Model系列GUI合成到项目中的指南
在工业自动化、智能终端HMI、车载仪表盘等领域,高性能的HMI(人机界面)芯片是不可或缺的核心组件。启明智显推出的Model系列(如Model3C、Model3、Model4)HMI芯片,以其卓越的性能和广泛的应用领域,…...

开源服务器运维工具1Panel
1Panel是杭州飞致云信息科技有限公司推出的一款现代化、开源的Linux服务器运维管理面板。 以下是对1Panel的详细介绍: 一、基本信息 产品名称:1Panel所属公司:杭州飞致云信息科技有限公司编写语言:Golang上线时间:20…...

新版本源2.0大模型发布:Yuan2-2B-July-hf
引言 近日,浪潮信息的新一代基础语言大模型源2.0 迎来了重要更新。浪潮信息正式发布了 Yuan2-2B-July-hf 模型,标志着源2.0系列模型在性能和功能上的进一步提升。这一版本将为开发者和研究人员提供更强大的工具,以满足各种语言处理需求。…...
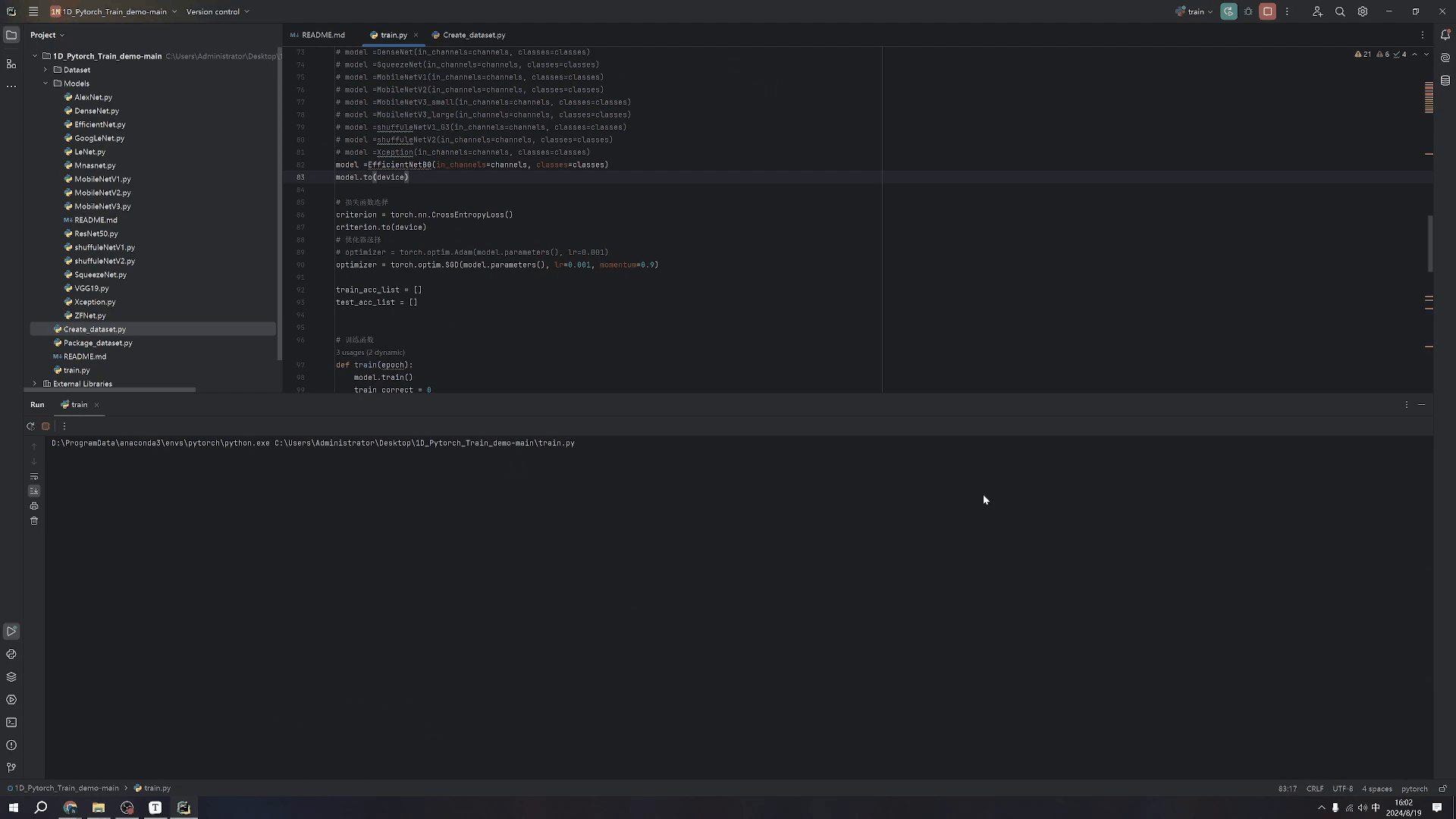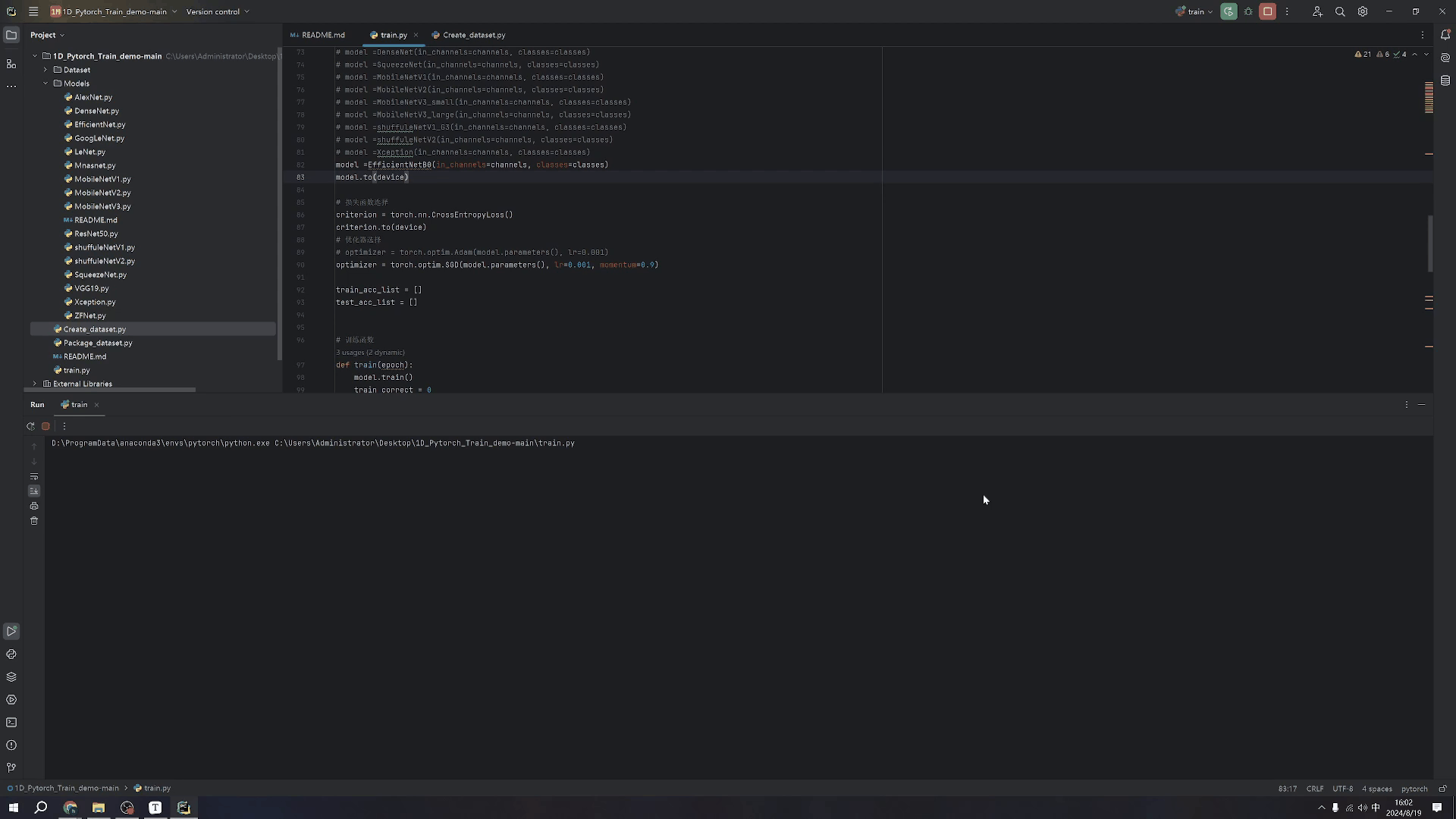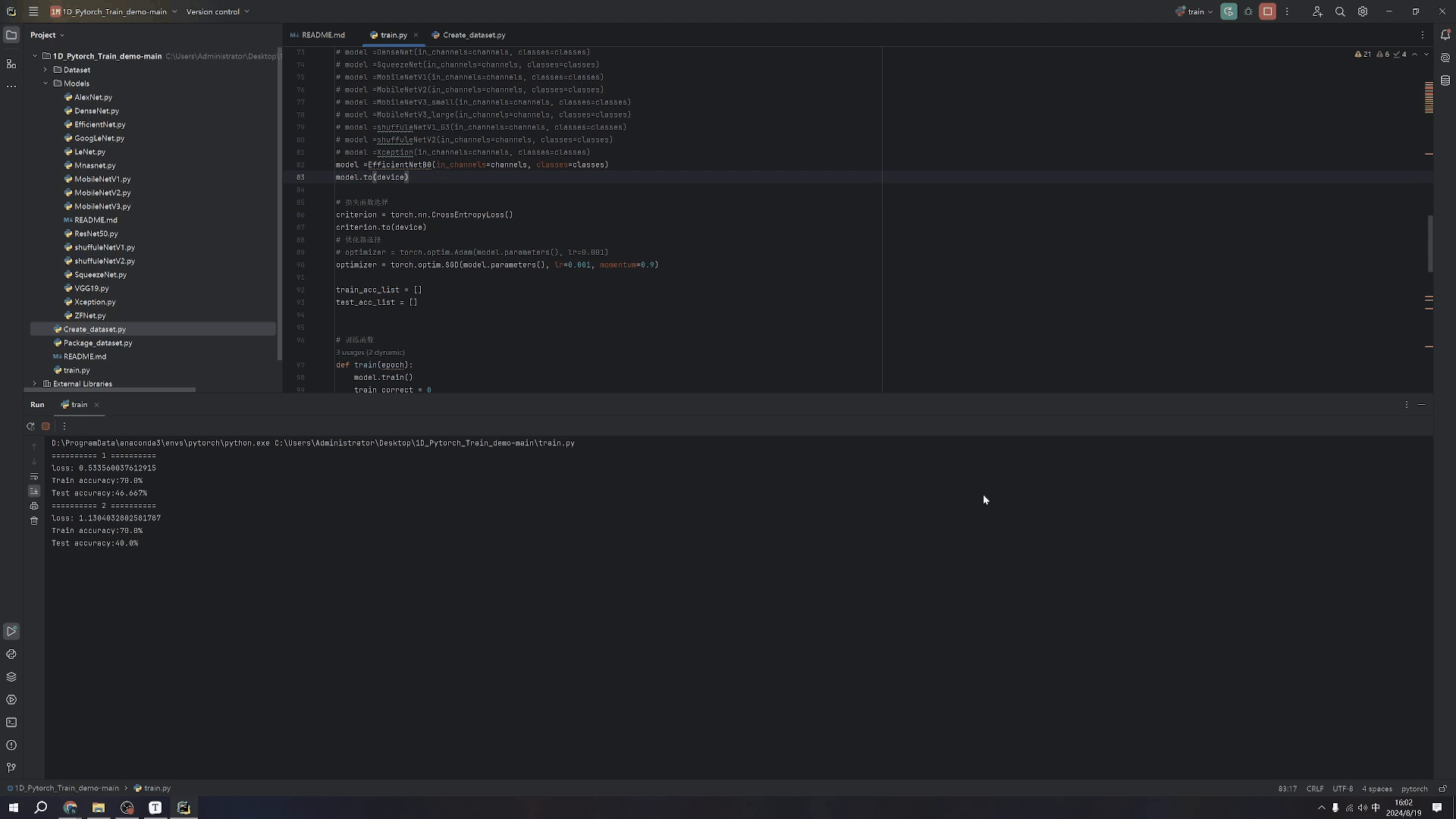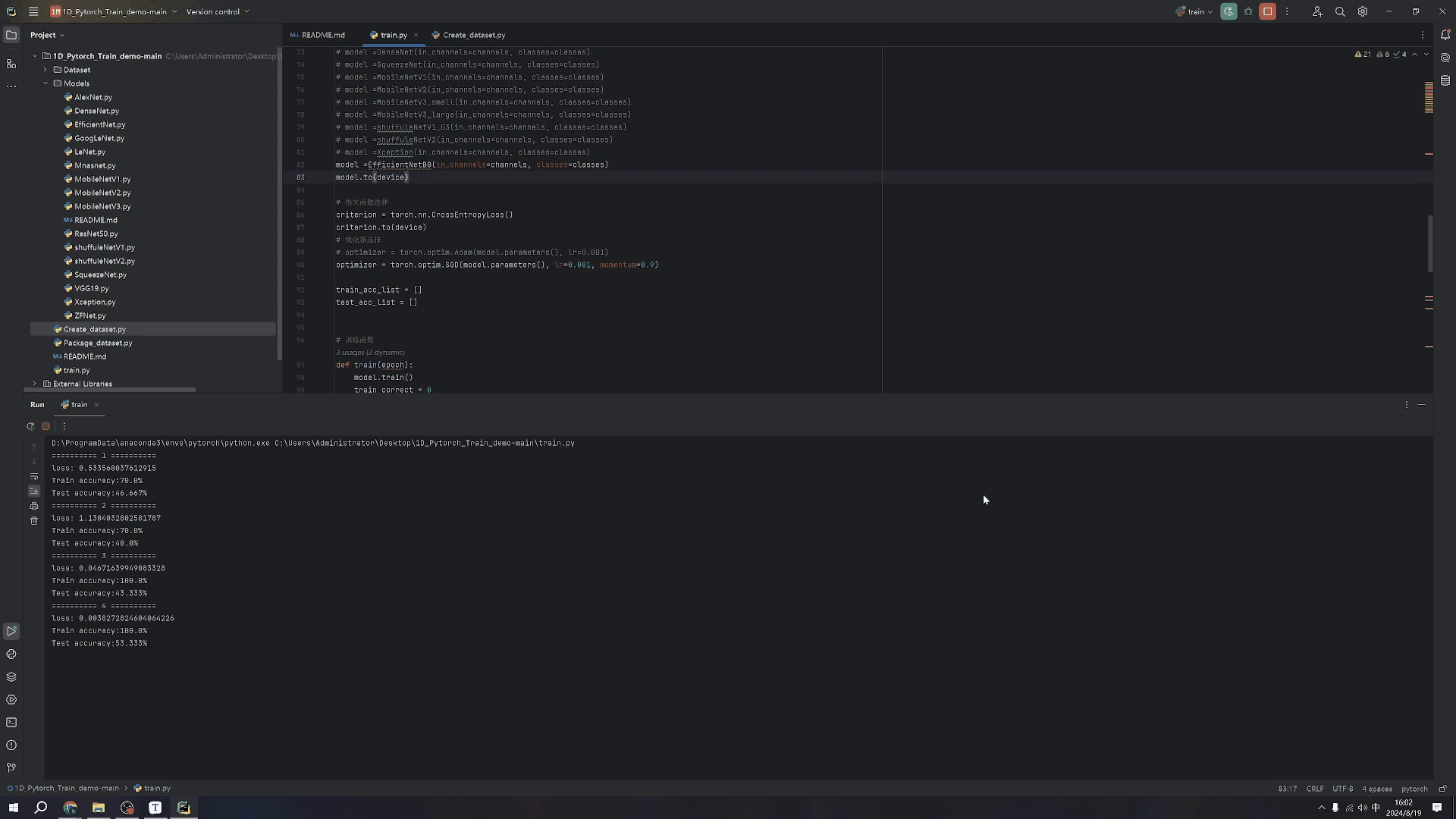
用python生成GIF动图—用于博客插图或封面等
生成GIF动图🚀 由于目前自己是在做大模型,还有一些树莓派硬件之类的东西,一是大模型的流式输出的例子需要用到GIF,二是做单片机的时候例如一些灯的闪烁和变化需要用到,所以之前也是一直有这个打算所以就记录一下这个生…...

[RCTF2019]draw
下载是一个文本文档,百度AI cs pu lt 90 fd 500 rt 90 pd fd 100 rt 90 repeat 18[fd 5 rt 10] lt 135 fd 50 lt 135 pu bk 100 pd setcolor pick [ red orange yellow green blue violet ] repeat 18[fd 5 rt 10] rt 90 fd 60 rt 90 bk 30 rt 90 fd 60 pu lt 90 f…...

设计模式 - 责任链模式
💝💝💝首先,欢迎各位来到我的博客!本文深入理解设计模式原理、应用技巧、强调实战操作,提供代码示例和解决方案,适合有一定编程基础并希望提升设计能力的开发者,帮助读者快速掌握并灵活运用设计模式。 💝💝💝如有需要请大家订阅我的专栏【设计模式】哟!我会定…...

jpg怎么转换成pdf?6个简单方法,实现jpg转换成pdf
你是否也曾想将jpg图片转换为pdf格式文档呢?亦或者在处理文档或制作报告时,不知道怎么才能更快地将多张图片整合成一个pdf文件呢?如果你正在寻找简单快速的方法,又有哪些工具可以帮助您完成图片转pdf呢?别着急…...

ptrade排坑笔记——使用量化交易的时候有报错提示!
前言 今天要和大家分享一个遇见的问题,有客户反馈,自己在使用量化交易的时候,会有报错!会在后文分享我们是如何解决这个问腿的! 一、问题描述 客户主要遇见的问题是,量化在进行交易的过程中,…...

C#-MemoryMarshal
MemoryMarshal 类是 .NET 中用于处理内存的工具类,它提供了一组静态方法,用于在托管代码中以安全和高效的方式操作内存块。MemoryMarshal 类主要用于处理原始内存数据而不需要进行复制,这对于性能关键的操作非常有用。 MemoryMarshal 类包含…...

Java并发编程的艺术
Java作为一门面向对象的编程语言,自1995年推出以来,一直以其稳定性、跨平台性和丰富的API受到广大开发者的喜爱。在Java的发展历程中,并发编程一直是其重要的特性之一。本文将探讨Java并发编程的艺术,解析其核心概念和常用并发工具…...
)
华为 OLT 添加 ONU 配置 (SNMP管理模式)
上网业务数据规划 OLT PON口 0/8/0 ONU_ID 0 ONU 序列号 4857544323BE233B 外层 VLAN ID 2012 内层VLAN ID 35 用户 FE 端口 ONU 0/1/1 用户VLAN 35 DBA带宽类型 Type 2 流量模板编号 10 DBA 模板编号 30 ONU线路模板编号 40 T-CONT (网管) 0 T-CONT(业务_ 2 GEM (网管) 0 …...

【JavaScript】[]和{} 的转换
背景 ([])? true:false ({})? true:false ([] true)? true:false ({} true)? true:false ([] true)? true:false ({} true)? true:false分析 [ ]和{ } 都是复杂类型,以上都是三目运算符判断 1.判断[ ]和{ } 是否存在 声明了这些已经分配了内存…...

C#关于多线程的线程问题
using System.Text; namespace 平时练习8._19day06 {internal class Program{static async Task Main(string[] args){Console.WriteLine(Thread.CurrentThread.ManagedThreadId );StringBuilder sb new StringBuilder();for (int i 0; i < 10000; i){sb.Append("…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
