矩阵中的最大得分(Lc3148)——动态规划
给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格(不必相邻)。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。
你可以从 任一 单元格开始,并且必须至少移动一次。
返回你能得到的 最大 总得分。
示例 1:

输入:grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]
输出:9
解释:从单元格 (0, 1) 开始,并执行以下移动:
- 从单元格 (0, 1) 移动到 (2, 1),得分为 7 - 5 = 2 。
- 从单元格 (2, 1) 移动到 (2, 2),得分为 14 - 7 = 7 。
总得分为 2 + 7 = 9 。
示例 2:
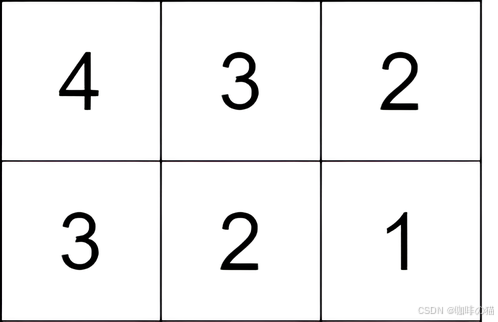
输入:grid = [[4,3,2],[3,2,1]]
输出:-1
解释:从单元格 (0, 0) 开始,执行一次移动:从 (0, 0) 到 (0, 1) 。得分为 3 - 4 = -1 。
提示:
m == grid.lengthn == grid[i].length2 <= m, n <= 10004 <= m * n <= 1051 <= grid[i][j] <= 105
问题简要描述:返回最大总得分
细节阐述:
- f[i][j] 表示以 (i,j) 为终点的路径的最小值
Java
class Solution {public int maxScore(List<List<Integer>> grid) {int m = grid.size(), n = grid.get(0).size();int[][] f = new int[m + 1][n + 1];int inf = 1 << 30, ans = -inf;for (int i = 0; i < m; i++) {for (int j = 0; j < n; j++) {int min = inf;if (i > 0) {min = Math.min(min, f[i - 1][j]);}if (j > 0) {min = Math.min(min, f[i][j - 1]);}ans = Math.max(ans, grid.get(i).get(j) - min);f[i][j] = Math.min(grid.get(i).get(j), min);}}return ans;}
}Python3
class Solution:def maxScore(self, grid: List[List[int]]) -> int:f = [[0] * len(grid[0]) for _ in range(len(grid))]ans = -inffor i, row in enumerate(grid):for j, x in enumerate(row):mi = infif i:mi = min(mi, f[i - 1][j])if j:mi = min(mi, f[i][j - 1])ans = max(ans, grid[i][j] - mi)f[i][j] = min(grid[i][j], mi)return ansTypeScript
function maxScore(grid: number[][]): number {const [m, n] = [grid.length, grid[0].length];const f = Array.from({length: m}, () => Array.from({length: n}, () => 0));let ans = -Infinity;for (let i = 0; i < m; i++) {for (let j = 0; j < n; j++) {let min = Infinity;if (i > 0) {min = Math.min(min, f[i - 1][j]);}if (j > 0) {min = Math.min(min, f[i][j - 1]);}ans = Math.max(ans, grid[i][j] - min);f[i][j] = Math.min(grid[i][j], min);}}return ans;
};C++
class Solution {
public:int maxScore(vector<vector<int>>& grid) {int m = grid.size(), n = grid[0].size();int f[m][n];int inf = 1 << 30, ans = -inf;for (int i = 0;i < m;i++) {for (int j = 0;j < n;j++) {int mi = inf;if (i > 0) {mi = min(mi, f[i - 1][j]);}if (j > 0) {mi = min(mi, f[i][j - 1]);}ans = max(ans, grid[i][j] - mi);f[i][j] = min(grid[i][j], mi);}}return ans; }
};Go
func maxScore(grid [][]int) int {m, n := len(grid), len(grid[0])f := make([][]int, m)for i := range f {f[i] = make([]int, n)}const inf int = 1 << 30ans := -inffor i, row := range grid {for j, x := range row {mi := infif i > 0 {mi = min(mi, f[i-1][j])}if j > 0 {mi = min(mi, f[i][j-1])}ans = max(ans, x-mi)f[i][j] = min(x, mi)}}return ans
}相关文章:

矩阵中的最大得分(Lc3148)——动态规划
给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格(不必相邻)。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。 你可以从 任一 单元格开始,并且必须…...
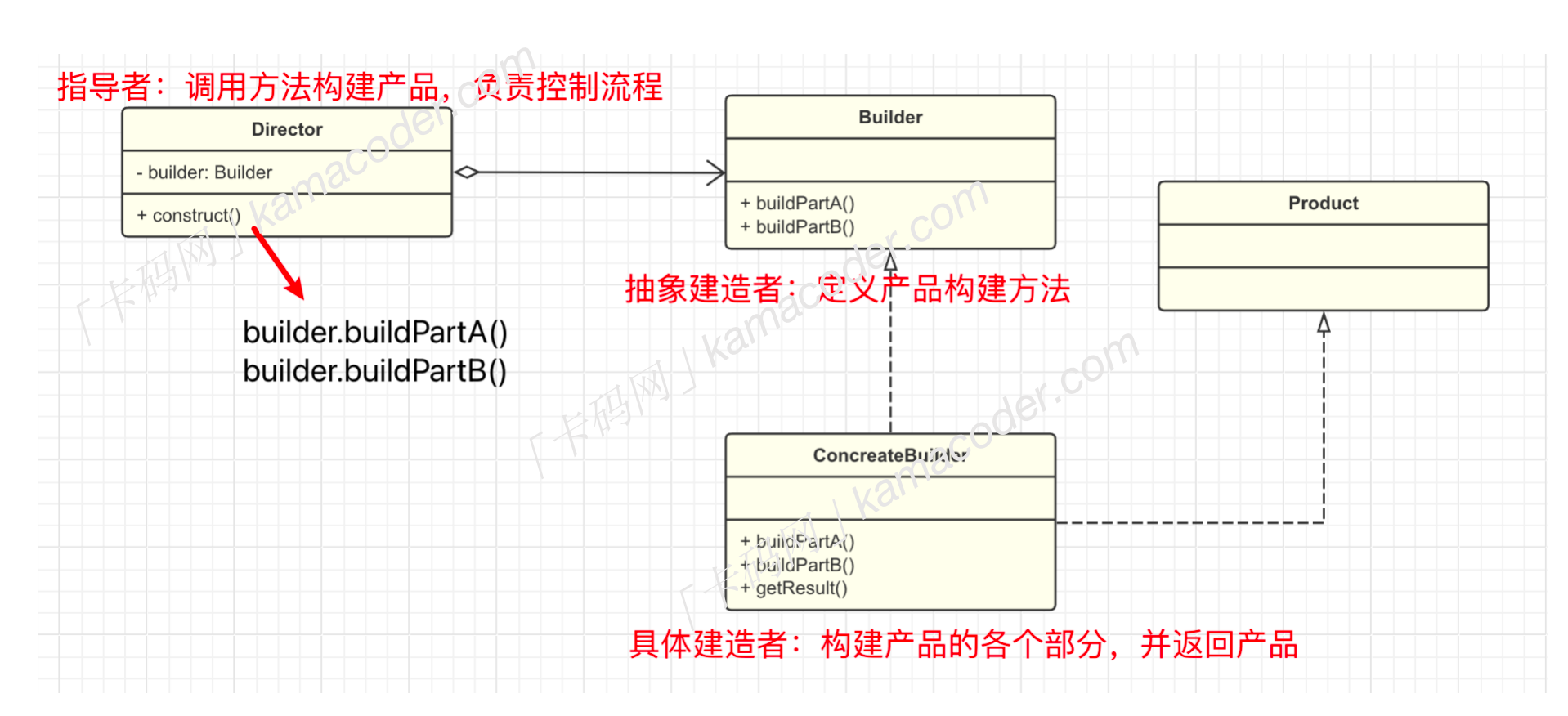
C++ 设计模式(4. 建造者模式)
建造者模式(也被成为生成器模式),是一种创建型设计模式,软件开发过程中有的时候需要创建很复杂的对象,而建造者模式的主要思想是将对象的构建过程分为多个步骤,并为每个步骤定义一个抽象的接口。具体的构建…...

Arbitrum 和 Optimism Layer 2 扩展方案对比
Arbitrum 和 Optimism 对比分析 Arbitrum 和 Optimism 是两个以太坊 Layer 2 扩展方案,它们都使用了 Optimistic Rollup 技术来提升以太坊的可扩展性并降低交易成本。虽然它们有着相似的目标,但在架构设计、性能表现和费用结构上各有特点。 一、架构与…...

热门的蓝牙耳机中,哪种类型更受欢迎?四款热度高的开放式耳机
在如今的耳机市场中,开放式耳机异军突起,成为了众多消费者的新宠。如果你还在为传统入耳式耳机带来的不适而烦恼,那么开放式耳机绝对值得你一试。它不仅能让你在享受音乐的同时,依然可以清晰感知周围环境,保障你的安全…...

基于web的亚热带常见自然林病虫害识别系统——总结与展望
文章目录 一、前言二、总结三、展望参考文献致谢一、前言 这个系列也迎来了结尾,最后说一些碎碎念… 二、总结 本文首先简要介绍了卷积神经网络的基本原理,以及在亚热带常见自然林植物识别领域的研究应用现状。 其重点研究了卷积神经网络在亚热带常见自然林植物叶片病害识…...

其他自动重试的注解
除了 Retryable 注解之外,Spring 提供了其他注解用于自动重试方法,主要包括以下几个注解: 1. Recover Recover 注解用于定义重试次数耗尽后执行的恢复方法。当 Retryable 注解的重试次数达到上限时,Recover 方法会被调用。这通常…...
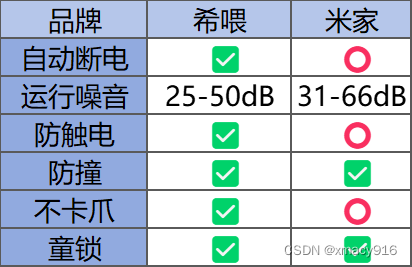
宠物空气净化器哪款能吸毛?希喂、米家宠物空气净化器测评分享
养猫最令人困扰的,就是掉毛与难以彻底消除的异味,这两个问题就成了养猫生活中的一大挑战。每当换季或是猫咪自我梳理时,家中便被一层细腻的绒毛覆盖,从地板到沙发,从床单到衣物,甚至是空气中都漂浮着细小的…...
)
讲清前端开发(入门)
前端开发:创建用户在网页或应用程序中直接与之交互的部分。 简单来说,就是负责打造用户在使用网站、网页应用或者移动应用时直接看到和与之交互的部分。打个比方,前端开发就像是给房子做装修。房子的框架结构已经有了,但是需要有…...

深入理解MySQL索引:原理、数据结构与优化策略
深入理解MySQL索引:原理、数据结构与优化策略 MySQL 是当今最流行的开源关系型数据库管理系统之一,其强大的性能与灵活的可扩展性使得它广泛应用于各种规模的应用程序中。在数据库的日常操作中,索引起着至关重要的作用,能够极大地…...

mysql数据库基础使用
1、登录mysql ① 本地登录 mysql -u 用户名 -p ②远程登入 mysql -h ip主机地址 -P 端口号 -u 用户名 -p 回车输入密码即可. 2、关于用户操作 ①创建用户 % 代表所有ip都可以访问,可指定主机ip create user 用户名% identified by 密码; ②修改密码 alte…...

GATK AlleleList接口介绍
在 GATK(Genome Analysis Toolkit)中,AlleleList 接口是一个用来表示等位基因(alleles)列表的接口。Allele 是遗传学中用于表示某一特定基因座的不同形式的一个基本单位。AlleleList 接口定义了一些操作,使得处理和访问一组等位基因更加方便。 AlleleList 的实现类和继承…...

直播App遭受抓包后的DDoS与CC攻击防御策略
随着直播应用的普及,越来越多的用户开始依赖这些平台进行娱乐和社交活动。然而,这也使得直播平台成为网络攻击的目标之一。其中,DDoS(分布式拒绝服务)攻击和CC(Challenge Collapsar,即HTTP慢速攻…...

【xilinx】 AXI Quad SPI IP - 如果 s_axi_wstrb 不等于 0xf,则寄存器可能无法正确更新
PG153 (v3.2) 规定如下: “AXI4-Lite 写访问寄存器由 32 位 AXI 写数据 (* _wdata ) 信号更新,并且不受 AXI 写数据选通 (* _wstrb ) 信号的影响。” "The AXI4-Lite write access register is updated by the 32-bit AXI Write Data (* _wdata ) s…...

【EPLAN】P8 2.9 使用不了ePLUSE
【更多软件使用问题请点击亿道电子官方网站】 1、 文档目标 解决 EPLAN P8 2.9 使用不了ePLUSE问题 2、 问题场景 客户反应 EPLAN P8 2.9 版本打开后使用不了 ePLUSE 功能,如图 1 所示 EPLAN ePLUSE 界面为空白状态,无法使用。 图 1 3、软硬件环境 …...

页面设计任务 个人简介页面
目录 任务要求 任务讲解 源码: 详细讲解 html部分 CSS部分 任务要求 页面结构: 创建一个基本的 HTML 页面,页面标题为“我的个人简介”。页面内容分为以下四个部分: 顶部导航栏: 包含至少三个导航链接,例如:“主页”、“关于…...

机械学习—零基础学习日志(如何理解概率论3)
随机变量的函数分布 一维随机变量分布,可以看到下图,X为不同情况的概率。而x如果是大于等于X,那么当x在40以内时,没有概率,为0。 当x变大,在40-80之间,那么x大于X的概率为,0.7&…...

YOLOv8添加SE注意力机制有效提升检测精度(已跑通)
SE注意力机制概念 SSqueeze-and-Excitation (SE) 注意力机制是一种专注于增强网络模型对不同特征通道的重要性理解的机制。它通过对通道维度上的特征进行动态调整,增强了网络对重要特征的敏感性。 源码 import numpy as np import torch from torch import nn fro…...

【正点原子K210连载】第三十二章 音频FFT实验 摘自【正点原子】DNK210使用指南-CanMV版指南
第三十二章 音频FFT实验 本章将介绍CanMV下FFT的应用,通过将时域采集到的音频数据通过FFT为频域。通过本章的学习,读者将学习到CanMV下控制FFT加速器进行FFT的使用。 本章分为如下几个小节: 32.1 maix.FFT模块介绍 32.2 硬件设计 32.3 程序设…...
Android Studio修改默认.m2与Gradle user home缓存位置
Android Studio修改默认.m2与Gradle user home缓存位置 1、修改Gradle user home的方法: android studio配置默认.gradle路径_android studio gradle在哪-CSDN博客文章浏览阅读2k次。当android studio新建一个项目时候,默认的.gradle路径均认为是在c盘的…...

BFS解决单源最短路问题
目录 迷宫中离入口最近的出口 最小基因变化 单词接龙 为高尔夫比赛砍树 迷宫中离入口最近的出口 题目 思路 使用宽度优先遍历解决这道题,需要一个二维数组标记是否被遍历过,也需要一个队列辅助完成宽度优先遍历,类似于水波纹一样&#x…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...
