面试题目:(4)给表达式添加运算符
目录
题目
代码
思路解析
例子
题目
- 题目
- 给定一个仅包含数字 0-9 的字符串 num 和一个目标值整数 target ,在 num 的数字之间添加 二元 运算符(不是一元)+、- 或 * ,
- 返回
- 所有能够得到 target 的表达式。
- 1 <= num.length <= 10
- num 仅含数字
- -231 <= target <= 231 - 1
- 注意
- 返回表达式中的操作数 不应该 包含前导零。
- 示例 1:
- 输入: num = "123", target = 6
- 输出: ["1+2+3", "1*2*3"]
- 解释: “1*2*3” 和 “1+2+3” 的值都是6。
- 示例 2:
- 输入: num = "232", target = 8
- 输出: ["2*3+2", "2+3*2"]
- 解释: “2*3+2” 和 “2+3*2” 的值都是8。
- 示例 3:
- 输入: num = "3456237490", target = 9191
- 输出: []
- 解释: 表达式 “3456237490” 无法得到 9191 。
代码
#include <stdlib.h>
#include <string.h>
#include <stdio.h>void evaluate(int* num_list, int* num_flag, int n, int target) {int end = num_list[0]; for (int i = 1; i < n; i++) {if (num_flag[i] == 1) {end *= num_list[i];} else if (num_flag[i] == 2) {end += num_list[i];} else if (num_flag[i] == 3) {end -= num_list[i];}}if (end == target) {printf("找到表达式: ");for (int i = 0; i < n; i++) {if (i > 0) {if (num_flag[i] == 1) printf("*");if (num_flag[i] == 2) printf("+");if (num_flag[i] == 3) printf("-");}printf("%d", num_list[i]);}printf(" = %d\n", target);}
}void backtrack(int* num_list, int* num_flag, int n, int target, int pos) {if (pos == n) {evaluate(num_list, num_flag, n, target);return;}for (int i = 1; i <= 3; i++) { // 遍历三种运算符num_flag[pos] = i;backtrack(num_list, num_flag, n, target, pos + 1);// 递归下一个运算符}
}int main() {char num[256] = "";int target;printf("num = ");fgets(num, sizeof(num), stdin);if (strlen(num) > 10) return 0;int n = strlen(num) - 1;int num_list[n];for (int i = 0; i < n; i++) {if (num[i] >= '0' && num[i] <= '9') {num_list[i] = num[i] - '0';} else {return 0;}}printf("target = ");scanf("%d", &target);if (target > 230 || target < -231) return 0;int num_flag[n]; // 保存操作符的数组backtrack(num_list, num_flag, n, target, 1);return 0;
}
思路解析
- 接收输入的字符串和目标数字
- 判断其是否输入正确
- 将字符串数字转为整数数组
- 调用递归backtrack函数,从第一位开始递归
- 判断递归索引是否是到最后一位
- 是的话调用验算函数
- 递归标志位数组进行判断加减算出答案
- 判断答案于目标数字是否一样,一样就打印
- 是的话调用验算函数
- 不是的话就继续就进行对标志位数组进行初始化
- 一个数字一个标志位,如果是1就表示乘法,2为加法,3为减法
- 递归索引+1进行递归
- 判断递归索引是否是到最后一位
简单来说就是先从第一个字符开始变化标志位,从1到2到3,也就从乘法加法减法,但在第一个执行乘法前,后面的要先完成从1到2到3的变化,所以就是在第一个执行1的时候要等第二个数字从1到2到3变化完才进行变2,然后又要等第二个数字从1到2到3才变3,如果有第三个数字的话第二个数字也要等第三个数字变化完,一层一层递归,直到递归到最后一个数字后,才开始进行计算
例子
输入 1234 目标 10

相关文章:

面试题目:(4)给表达式添加运算符
目录 题目 代码 思路解析 例子 题目 题目 给定一个仅包含数字 0-9 的字符串 num 和一个目标值整数 target ,在 num 的数字之间添加 二元 运算符(不是一元)、- 或 * ,返回 所有能够得到 target 的表达式。1 < num.length &…...

[C#]将opencvsharp的Mat对象转成onnxruntime的inputtensor的3种方法
第一种方法:在创建tensor时候直接赋值改变每个tensor的值,以下是伪代码: var image new Mat(image_path);inpWidth image.Width;inpHeight image.Height;//将图片转为RGB通道Mat image_rgb new Mat();Cv2.CvtColor(image, image_rgb, Col…...

CTF入门教程(非常详细)从零基础入门到竞赛,看这一篇就够了!
一、CTF简介 CTF(Capture The Flag)中文一般译作夺旗赛,在网络安全领域中指的是网络安全技术人员之间进行技术竞技的一种比赛形式。CTF起源于1996年DEFCON全球黑客大会,以代替之前黑客们通过互相发起真实攻击进行技术比拼的方式。…...

数据链路层 I(组帧、差错控制)【★★★★★】
(★★)代表非常重要的知识点,(★)代表重要的知识点。 为了把主要精力放在点对点信道的数据链路层协议上,可以采用下图(a)所示的三层模型。在这种三层模型中,不管在哪一段…...

悟空降世 撼动全球
文|琥珀食酒社 作者 | 积溪 一只猴子能值多少钱? 答案是:13个小目标 这两天 只要你家没有断网 一定会被这只猴子刷屏 它就是咱国产的3A游戏 《黑神话:悟空》 这只猴子到底有多火? 这么跟你说吧 茅台见了它都…...

Swoole 和 Java 哪个更有优势呢
Swoole 和 Java 各有优势,在性能上不能简单地说哪一个更好,需要根据具体的应用场景来分析。 Swoole 优势:高并发:Swoole 是一个基于 PHP 的异步、协程框架,专为高并发场景设计,适用于 I/O 密集型应用&…...
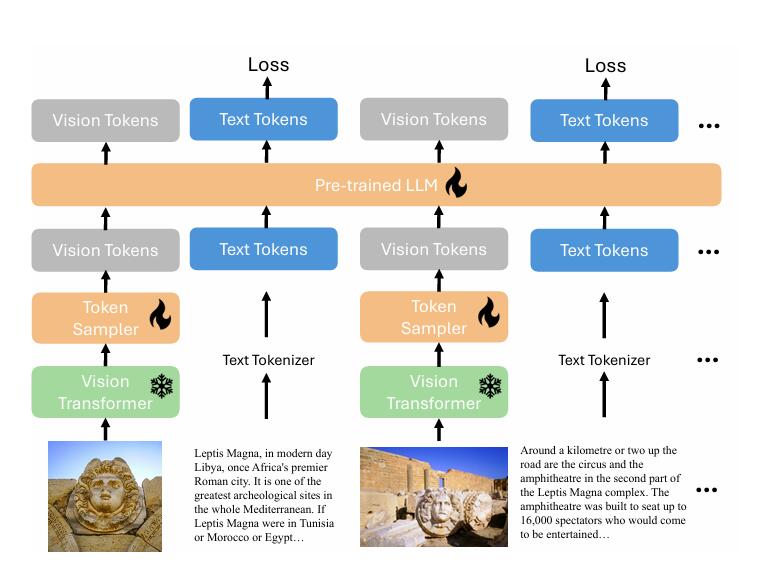
Salesforce 发布开源大模型 xGen-MM
xGen-MM 论文 在当今 AI 技术飞速发展的时代,一个新的多模态 AI 模型悄然崛起,引起了业界的广泛关注。这个由 Salesforce 推出的开源模型—— xGen-MM,正以其惊人的全能特性和独特优势,在 AI 领域掀起一阵旋风。那么,x…...

冒 泡 排 序
今天咱们单独拎出一小节来聊一聊冒泡排序昂 冒泡排序的核心思想就是:两两相邻的元素进行比较(理解思路诸君可看下图) 接下来我们上代码演示: 以上就是我们初步完成的冒泡排序,大家不难发现,不管数组中的元…...

采用先进的人工智能视觉分析技术,能够精确识别和分析,提供科学、精准的数据支持的智慧物流开源了。
智慧物流视频监控平台是一款功能强大且简单易用的实时算法视频监控系统。它的愿景是最底层打通各大芯片厂商相互间的壁垒,省去繁琐重复的适配流程,实现芯片、算法、应用的全流程组合,从而大大减少企业级应用约95%的开发成本可通过边缘计算技术…...

IAA游戏APP如何让合理地让用户观看更多广告,提高广告渗透率
广告变现已经成为休闲游戏开发者重要的收益方式之一,超50%国内休闲游戏已经采用广告变现的方式,游戏广告预算是游戏行业开发者广告变现的主要预算来源。 #深度好文计划#如何合理地提高广告渗透率? 广告渗透率能直接反映游戏中有广告行为用户…...

环网交换机的特殊作用是什么?
环网交换机作为现代网络建设的重要组成部分,具有独特而特殊的作用。在信息技术迅猛发展的今天,各类数据传输和网络连接需求日益增加,环网交换机的出现为解决这些问题提供了理想的方案。环网交换机通常将多个网络节点通过环形结构连接起来&…...

mac电脑安装Zsh并启用
安装 Zsh 1. 安装 Zsh 新版mac系统会默认安装并使用zsh,如没用,需在终端中安装: brew install zsh2. 安装 Oh My Zsh 克隆Oh My Zsh到你的目录: git clone https://github.com/robbyrussell/oh-my-zsh.git ~/.oh-my-zsh3. 复…...

【后续更新】python搜集上海二手房数据
源码如下: import asyncio import aiohttp from lxml import etree import logging import datetime import openpyxlwb = openpyxl.Workbook() sheet = wb.active sheet.append([房源, 房子信息, 所在区域, 单价, 关注人数和发布时间, 标签]) logging.basicConfig(level=log…...
创建GPTs,打造你的专属AI聊天机器人
在2023年11月的「OpenAI Devday」大会上,OpenAI再度带来了一系列令人瞩目的新功能,其中ChatGPT方面的突破尤为引人关注。而GPTs的亮相,不仅标志着个性化AI时代的到来,更为开发者和普通用户提供了前所未有的便利。接下来࿰…...
)
深度学习 vector 之模拟实现 vector (C++)
1. 基础框架 这里我们有三个私有变量,使用 _finish - _start 代表 _size,_end_of_storage - _start 代表 _capacity,并且使用到了模版,可以灵活定义存储不同类型的 vector,这里将代码量较小的函数直接定义在类的内部使…...

关于LLC知识10
在LLC谐振腔中能够变化的量 1、输入电压 2、Rac(负载) 所以增益曲线为红色(Rac无穷大)已经是工作的最大极限了,LLC不可能工作在红色曲线之外 负载越重时,增益曲线越往里面 假设: 输入电压…...

最长的严格递增或递减子数组
给你一个整数数组 nums 。 返回数组 nums 中 严格递增 或 严格递减 的最长非空子数组的长度。 示例 1: 输入:nums [1,4,3,3,2] 输出:2 解释: nums 中严格递增的子数组有[1]、[2]、[3]、[3]、[4] 以及 [1,4] 。 nums 中…...

【JavaEE】SpringBoot 统一功能处理:拦截器、统一数据返回与异常处理的综合应用与源码解析
目录 SpringBoot 统⼀功能处理拦截器拦截器快速⼊⻔拦截器详解拦截路径拦截器执⾏流程 登录校验定义拦截器注册配置拦截器 DispatcherServlet 源码分析(了解)初始化(了解) DispatcherServlet的初始化1. HttpServletBean.init()2. FrameworkServlet.initServletBean() WebApplic…...

I2C学习:上拉电阻选取
一.I2C简介 I2C总线是由Philips公司开发的一种简单、双向二线制同步串行总线。I2C总线在使用时,需要接上拉电阻,这是因为I2C接口是开漏输出,如图1所示。 图1 I2C开漏输出 I2C有5种速度模式:标准(100KHz&am…...

AC自动机-1
AC自动机(Aho-Corasick Automaton)是一种高效的多模式字符串匹配算法。它是由Alfred Aho和Margaret Corasick在1975年提出的。这种算法可以在一次扫描输入文本的情况下,同时查找多个模式串。 基本概念 Trie树 AC自动机是基于字典树数据结构构建的字典树…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
