python-逆序数(赛氪OJ)
[题目描述]
在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。比如一个元素个数为 4 的数列,其元素为 2,4,3,1,则 (2,1),(4,3),(4,1),(3,1) 是逆序,逆序数是4。现在求给定数列的逆序数。
输入格式:
输入共两行。
第一行为 N ,表示数列的元素个数。
第二行为 N 个用空格隔开的整数。
输出格式:
输出占一行,为逆序数的个数。
样例输入
4
2 4 3 1
样例输出
4
数据范围
对于 100% 的数据,保证1≤N≤2000,且每个整数的值都在int范围内。
来源/分类(难度系数:四星)
逆序对
完整代码展示:
n=int(input())
m=list(map(int,input().split()))
sum=0
for i in range(0,len(m)):
for j in range(i+1,len(m)):
if m[i]>m[j]:
sum+=1
print(sum)
代码解释:
“n=int(input()) ”,让用户输入数列中元素的个数n。
“m=list(map(int,input().split())) ”,让用户输入n个元素各自的值,并将其储存在列表m中。
“sum=0
for i in range(0,len(m)):
for j in range(i+1,len(m)):
if m[i]>m[j]:
sum+=1 ”,令sum=0,依次遍历m中元素,接着查找该元素后面是否存在大于该元素的元素(每查找到一个,就令sum+1)。
“print(sum) ”,打印sum的最终结果。
运行效果展示:


(声明:以上内容均为原创)
相关文章:

python-逆序数(赛氪OJ)
[题目描述] 在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。比如一个元素个数为 4 的数列,其元素为 2,4,3,1,则 (2,…...

PCIE-flit mode retry
下一个即将发送的seq num: 下一个即将发送的ack或者nak的seq num: Tx发送exp seq num的个数: Tx发送nak的个数 下一个期望收到的flit的seq num,注意是指下个期望收到的有效的、non-idle、non_duplictae的flit: 收到的flit的真实的seq num(implicit…...

使用Obsidian实现Anki快速制卡
文章目录 前言准备双双启用遇到问题查看是什么问题解决问题 开始使用使用前的一些设置快速制卡 前言 我现在使用 Anki 的同时也使用 Obsidian,正好可以通过插件来让这两个十分好用的软件实现联动。 在 Obsidian 中实现 Anki 的快速制卡。 准备 首先要在这两个软…...

Python编程:从入门到实践书籍介绍
对于Python入门的书籍推荐,以下是五本详细讲解的书籍,它们各自具有不同的特点和适用对象: 1. 《Python编程:从入门到实践》 作者:埃里克马瑟斯(Eric Matthes)《Python编程:从入门到实践》是一本经典的Pyth…...

Vue 3 的 emit 简单使用
在 Vue 3 中使用 emit,子组件可以将事件通知父组件,父组件可以在响应这些事件时执行特定的逻辑。 emit 是一种非常灵活的通信方式,允许组件之间以解耦的方式进行交互。 1. 基本用法 1、使用 defineEmits 子组件 <template><div…...

java在实际开发中反常识bug
目录 1.背景 2.案例 1.包装类型拆箱导致空指针异常 2.switch传入null,导致空指针异常 3.Arrays.asList添加异常 4.转BigDecimal类型时精度丢失 5.除以0不一定抛异常 6.Steam filter后集合修改,会修改原数据 3.完美&评论 1.背景 这篇博客,将列举本人在实际开发中看…...
重排序与Happens-Before)
java多线程(三)重排序与Happens-Before
一、重排序 1.1 指令重排定义和含义 定义:重排序是指编译器和处理器为了提高程序执行效率,在不改变单线程程序执行结果的前提下,对指令执行顺序进行重新排列的一种优化手段。 重排序可以发生在编译器优化阶段,也可以发生在处理…...

RUST知识框架与学习框架
RUST知识框架与学习框架 Rust是一门系统级编程语言,以其内存安全、高性能和并发性而著称,特别适用于开发低级系统、网络服务和并发应用,具有广泛应用前景。 一、Rust知识框架 基础语法与核心概念 变量与类型:包括基本数据类型、…...

git cherry-pick命令使用分享
在日常开发中,有时候会遇到一种情况,线上出了问题,但是现在的预生产环境(Pre-production Environment)或准生产环境(Stage Environment)有还未通过验收的内容,那么想进行修复可以选择…...

关闭Chrome快捷键
chrome是没办法改变快捷键以及屏蔽快捷键的,需要安装插件:shortkey 保证插件是开启的 不用做其他设置所有快捷键已被关闭...

常见DDoS攻击之零日漏洞Zero-day Attacks
目录 一、什么是零日漏洞Zero-day Attacks 二、零日漏洞是如何转化为零日攻击的 三、常见的零日攻击类型 四、为什么零日攻击很危险 五、著名的零日攻击事件 六、如何降低零日攻击的风险 七、DDoS攻击防御解决方案(定制化) 7.1 产品优势 7.2 产品…...

【字符串】Z函数 - 模板
z [ i ] z[i] z[i] 表示字符串 s s s 和 s [ i , n − 1 ] s[i,\ n - 1] s[i, n−1] 的最长前缀的长度,特别的, z [ 0 ] 0 z[0]0 z[0]0 // *********Z函数************** // - 时间复杂度 O(n) vector<int> z_function(string s) {int n (int…...

MySQL范围分区分区表
什么是范围分区分区表? 范围分区是一种根据某个列的范围值来分割表数据的分区方式。在范围分区中,每个分区都有自己的范围条件,当插入数据时,MySQL会根据指定的范围条件将数据分配到相应的分区中。这种分区方式可以使得表的数据按…...

网络UDP报文详细解析
目录 一、简介二、详细介绍三、其他相关链接1、TCP报文段的详细图总结2、TCP三次握手和四次挥手详解3、socket通信原理及相关函数详细总结4、网络包IP首部详细解析 一、简介 本文主要介绍UDP报文格式。 二、详细介绍 UDP是一种无连接、不可靠的用户数据报协议,其…...

望繁信科技入选2024年第3批上海市高新技术成果转化项目名单
近日,上海望繁信科技有限公司(以下简称“望繁信科技”)凭借其自主研发的“数字北极星流程挖掘分析软件”项目,成功入选2024年第3批上海市高新技术成果转化项目名单。这一殊荣根据《上海市高新技术成果转化项目认定办法》ÿ…...

深入探讨MySQL的锁机制:全局锁、表级锁和行级锁
深入探讨MySQL的锁机制:全局锁、表级锁和行级锁 在数据库管理中,锁机制是确保数据一致性和并发控制的重要手段。MySQL提供了多种锁策略,包括全局锁、表级锁和行级锁。本文将详细探讨这些锁机制的概念、使用场景及其示例代码,帮助…...
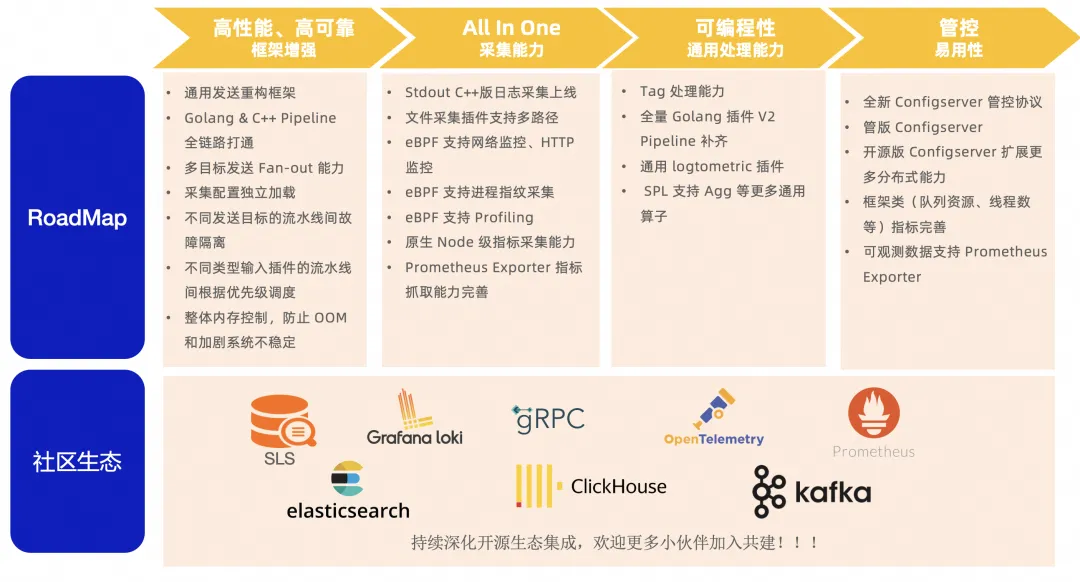
iLogtail 开源两周年:感恩遇见,畅想未来
早在上世纪 60 年代,早期的计算机(例如 ENIAC 和 IBM 的大型机)在操作过程中会输出一些基本的状态信息和错误报告,这些记录通常通过打印机输出到纸带或纸卡上,用于跟踪操作流程和调试,最早期的日志系统借此…...

写给大数据开发:在Databricks中自定义函数
你是否曾经在处理海量数据时感到力不从心?是否在重复编写相似代码时感到厌烦?如果是,那么Databricks中的自定义函数可能就是你一直在寻找的救星。在接下来的5分钟里,让我们一起探索如何利用这个强大的工具来revolutionize你的大数据开发工作流程。 目录 为什么要在Databrick…...

VMware vSphere Client无法访问和连接ESXi虚拟主机解决思路
文章目录 前言1. 问题现象2. 问题原因3. 解决方法4. 参考文章 前言 注意 : 可以先看看参考文章那里,在回过来看 1 、 2 、3 1. 问题现象 版本:VMware vCenter Server 5.5.0 build-2442329 问题描述:用VMware vSphere Client 登录ESXI主机出…...

实现Kruskal算法连通游戏地图地牢
前置知识 c分享|并查集从入门到出门 - 力扣(LeetCode) 彻底搞懂克鲁斯卡尔(Kruskal)算法(附C代码实现) - QuanHa - 博客园 (cnblogs.com) 白色点矩形是地牢,其中白线是按照krsukal…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
