【数据结构初阶】二叉树--基本概念
hello!

目录
一、树
1.1 树的概念和结构
1.2 树的相关术语
1.3 树的表示
1.4 树形结构实际应用场景
二、二叉树
2.1 概念和结构
2.2 特殊的二叉树
2.2.1 满二叉树
2.2.2 完全二叉树
2.3 二叉树的存储结构
2.3.1 顺序结构
2.3.2 链式结构
Relaxing Time!
—————————— 爱的华尔兹 ——————————
一、树
1.1 树的概念和结构
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成的一个具有层次关系的集合。树,顾名思义,因为它看起来像一个倒挂的树,也就是说它根朝上,叶朝下。
- 有一个特殊的结点,称为根节点,根节点没有前驱结点。
- 除根结点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、...、Tm,其中每一个集合Ti(1<=i<=m)又是一棵结构与树类似的子树。每棵子树的结点有且只有一个前驱,可以有0个或多个后继。因此,树是递归定义的。
- 子树是不能相交的。(如果相交就是图了)。
- 除了根结点之外,每个结点有且只有一个父结点。
- 一棵N个结点的树有N-1条边。

【注意】
树形结构中,子树之间不能有交集,否则就不是树形结构。
非树形结构:

1.2 树的相关术语

父结点/双亲结点:若一个结点含有子结点,则这个结点称为其子结点的父结点;如上图中的A是B的父结点。
子结点/孩子结点:一个结点含有的子树的根结点称为该结点的子结点,;B是A的子结点。
结点的度:一个结点有几个孩子,它的度就是多少;A的度为6,E的度为2。
树的度:一棵树中,最大的结点的度称为树的度;;该树的度为6。
叶子结点/终端结点:度为0的结点称为叶结点;B、C、O、P结点等都为叶子结点。
分支结点/非终端结点(非叶子结点):度不为0的结点;A、D、E等结点。
兄弟结点:具有相同父结点的结点互称为兄弟结点(亲兄弟);M和N为兄弟结点。
结点的层次:从根开始定义起,根为第一层,根的子结点为第二层,以此类推。
树的高度或深度:树中结点的最大层次;上图树的高度为4。
结点的祖先:从根到该结点所经分支上的所有结点;A是所有结点的祖先。
路径:一条从树中任意结点出发,沿父结点到子结点连接,达到任意结点的序列;如,从A到P的路径为:A-E-J-P,H到P:H-D-A-E-J-P。
子孙:以某结点为根的子树中任一结点都称为该结点的子孙。上图中,所有结点都为A的子孙。
森林:由m(m>0)棵互不相交的集合称为森林。
1.3 树的表示
树结构相对线性表更复杂,要存储起来比较麻烦,既要保存值域,又要保存结点和结点之间的关系。实际中树有很多表示方法如:双亲表示法,孩子表示法,孩子双亲表示法以及孩子兄弟表示法等。我们先简单了解一下其中最常用的孩子兄弟表示法。
struct TreeNode
{struct Node* child; //左边开始的第一个孩子结点struct Node* brother;//指向其右边的下一个兄弟结点int data; //结点中的数据域
}
1.4 树形结构实际应用场景
文件系统是计算机存储和管理文件的一种方式,它利用树形结构来组织和管理文件和文件夹。在文件系统中,树结构被广泛应用,它通过父结点和子结点之间的关系来表示不同层级文件和文件夹之间的关联。


二、二叉树
2.1 概念和结构
在树形结构中,我们最常用的就是二叉树,一棵二叉树是结点的一个有限集合,该集合由一个根结点加上两棵别称为左子树和右子树的二叉树组成或者为空。

从图中看出二叉树具备以下特点:
- 二叉树不存在度大于2的结点(二叉树只存在度为0,1,2);
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树;
【注意】对于任意二叉树都是由以下几种情况复合而成的。


2.2 特殊的二叉树
2.2.1 满二叉树
一个二叉树,如果每一层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^(k-1),则它就是满二叉树。(结点总数由等比数列求和得出)

2.2.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
通俗点来讲,假设二叉树层次为k,除了第k层之外,每层结点的个数都达到了最大结点数,第k层结点个数不一定达到最大结点数,完全二叉树结点的顺序是从左到右的。

满二叉树一定是完全二叉树,但是,完全二叉树不一定是满二叉树。
根据满二叉树的特点可知:
- 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点;
- 若规定根结点的层数为1,则深度为h的二叉树的最大结点数是2^h -1;
- 若规定根结点的层数为1,具有n个结点的满二叉树的深度h=log2(n+1),log以2为底,n+1为对数。
2.3 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
2.3.1 顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费,完全二叉树更适合使用顺序结构存储。

现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储,需要注意的是这里的堆和操作系统模拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
2.3.2 链式结构
二叉树的链式存储结构是指,用链表来表示一棵二叉树,,即用链来指示元素的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左右孩子所在的链结点的存储地址。链式结构又分为二叉链和三叉链,当前我们学习一般都是二叉链。后面会学习到三叉链。



至此,二叉树的相关概念学习结束!
完——
Relaxing Time!
———————————— 爱的华尔兹 ————————————
【爱的华尔兹_俞灏明_高音质在线试听_爱的华尔兹歌词|歌曲下载_酷狗音乐】

我是云边有个稻草人
期待我们的下一次相遇!
相关文章:

【数据结构初阶】二叉树--基本概念
hello! 目录 一、树 1.1 树的概念和结构 1.2 树的相关术语 1.3 树的表示 1.4 树形结构实际应用场景 二、二叉树 2.1 概念和结构 2.2 特殊的二叉树 2.2.1 满二叉树 2.2.2 完全二叉树 2.3 二叉树的存储结构 2.3.1 顺序结构 2.3.2 链式结构 …...

Pytorch添加自定义算子之(12)-开闭原则设计tensorrt和onnxruntime推理语义分割模型
一、开闭原则 开闭原则是SOLID原则中的一个,指的是尽量使用开放扩展,关闭修改的设计原则。 在C++中如何使用开闭原则导出动态库,可以按照以下步骤进行: 定义抽象基类:定义动态库中的抽象基类,该基类应该封装可扩展的接口。 实现派生类:实现基类的派生类,这些派生类将封…...

第二百零九节 Java格式 - Java数字格式类
Java格式 - Java数字格式类 以下两个类可用于格式化和解析数字: java.text.NumberFormatjava.text.DecimalFormat NumberFormat 类可以格式化一个数字特定地区的预定义格式。 DecimalFormat 类可以格式化数字以特定区域设置的自定义格式。 NumberFormat类的 getXXXInstance…...

LSI-9361阵列卡笔记
背景 要将raid0更改为JBOD直通模式 注意的点是要先将raid模式调整为JBOD之后重启机器,即可 备注:转换过程中硬盘中的数据未丢失。 步骤贴图 refer https://zhiliao.h3c.com/questions/dispcont/123250 https://blog.csdn.net/GreapFruit_J/article/…...

ArcGIS热点分析 (Getis-Ord Gi*)——基于地级市尺度的七普人口普查数据的热点与冷点分析
先了解什么是热点分析 ? 热点分析 (Getis-Ord Gi*) 是一种用于空间数据分析的技术,主要用于识别地理空间数据中值的聚集模式,可以帮助我们理解哪些区域存在高值或低值的聚集,这些聚集通常被称为“热点”或“冷点”,Gi* 统计量为…...

ASIACRYPT 2021
分类文章编号获奖论文1-3后量子密码4-9多方计算10-15物理攻击,泄露和对策16-21理论22-27公钥密码和鉴权密钥交换28-33高级加密和签名34-39对称密钥构建40-46量子安全47-53获奖论文54对称密码分析55-66增强型公钥加密和时间锁难题67-72同态加密和加密搜索73-77NIZK和SNARK78-80…...
C#学习之路day1
目录 一、概念:.net和c# 二、.net发展方向 三、.Net两种交互模式 四、创建项目 五、vs的组成部分 六、我的第一个C#程序 七、多个项目时启动项目的设置 八、注释 九、快捷键 一、概念:.net和c# 1、.net/dotnet :一般指.Net Framework框架&#…...
【安当产品应用案例100集】010-基于国密UKEY的信封加密应用案例
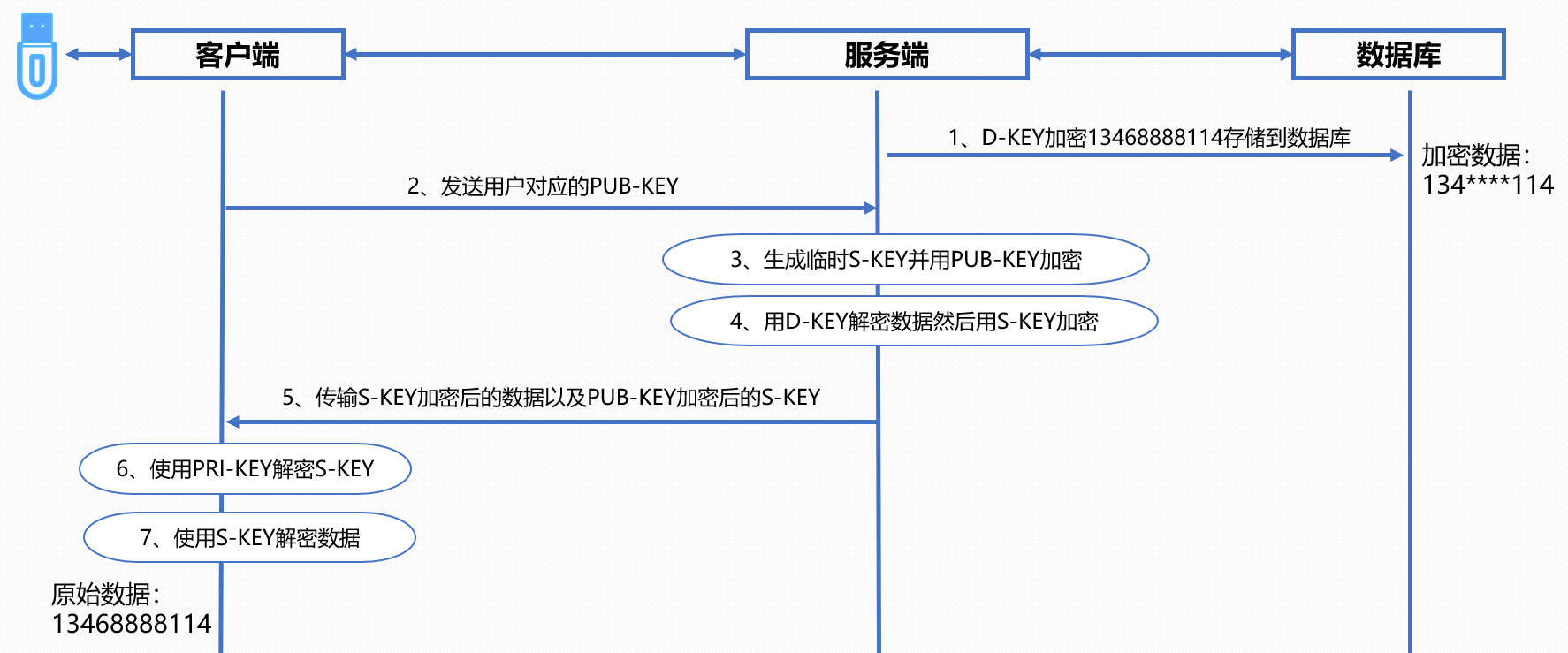
安当有个客户开发了一套C/S架构的软件,Server在云端,Client由不同的用户使用。最初软件设计开发的时候,没有考虑数据安全形势日渐严峻的问题,Server端和Client端直接就建立一个socket连接来进行通信,Server端发出去的数…...
扫码点餐系统小程序功能分析
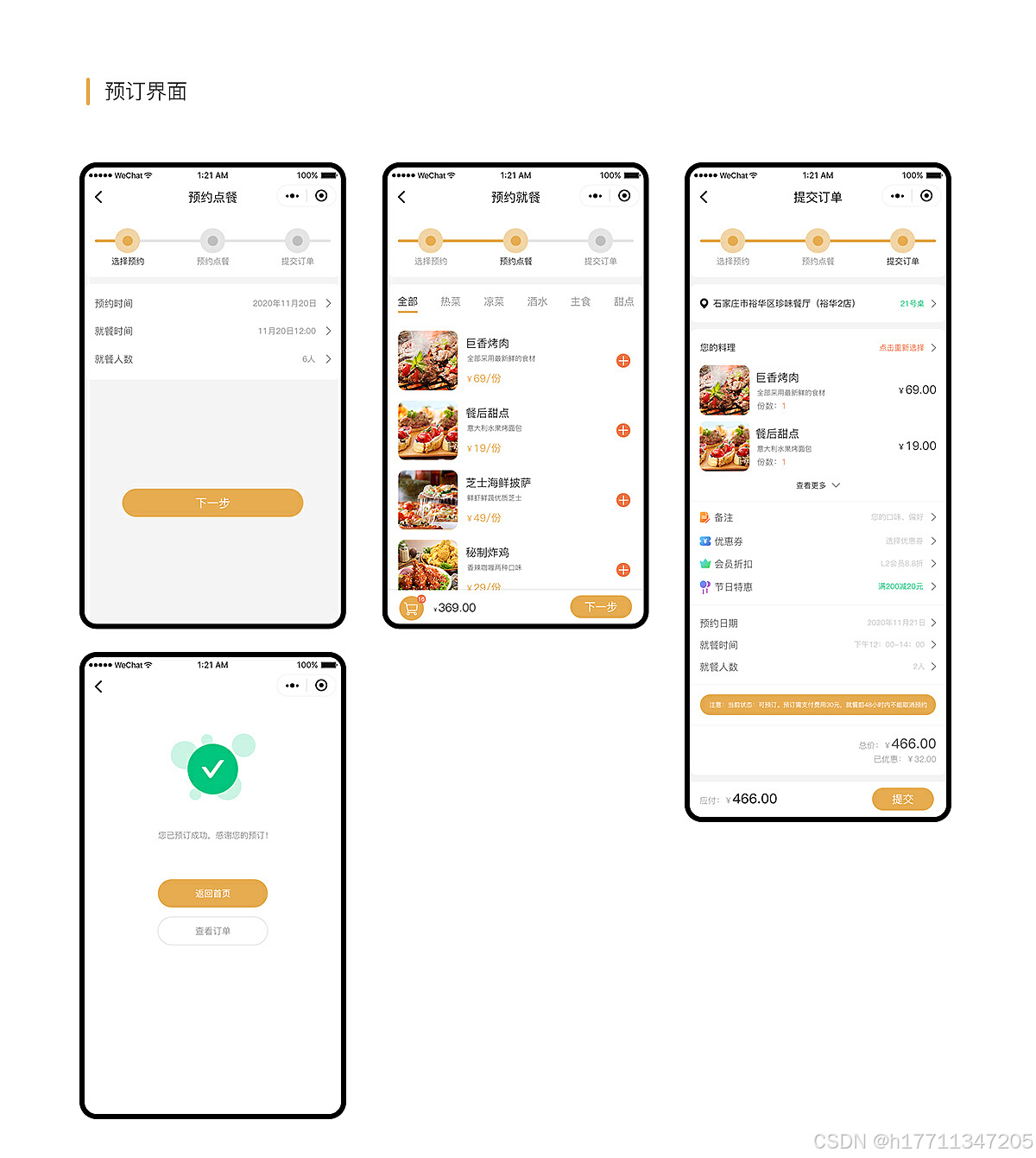
扫码点餐系统小程序通常具备以下核心功能: 用户界面:提供直观易用的界面,方便用户浏览菜单、选择菜品、查看订单状态等 。菜单展示:展示餐厅的菜单,包括菜品图片、价格、描述等信息 。扫码点餐:用户通过…...

网络安全——基础知识记忆梳理
1. SQL注入攻击 SQL注入攻击是一种常见的网络安全威胁,它利用Web应用程序中对用户输入的数据的不正确处理,攻击者可以在SQL查询中注入恶意代码,从而执行非授权的数据库操作。这种攻击方式可以导致数据泄漏、数据篡改、绕过认证等多种安全问题…...

GitHub开源的轻量级文件服务器,可docker一键部署
文件服务器 介绍安装使用命令使用API调用 介绍 项目github官网地址 Dufs是一款由Rust编写的轻量级文件服务器,不仅支持静态文件服务,还能轻松上传、下载、搜索文件,甚至支持WebDAV,让我们通过Web方式远程管理文件变得轻而易举。…...

Scratch编程深度探索:解锁递归与分治算法的奥秘
标题:Scratch编程深度探索:解锁递归与分治算法的奥秘 在编程的世界里,递归和分治算法以其精妙的逻辑结构和解决问题的能力而著称。Scratch,这款专为儿童和初学者设计的图形化编程工具,是否能够支持实现这样复杂的逻辑…...
使用docker compose一键部署 Portainer
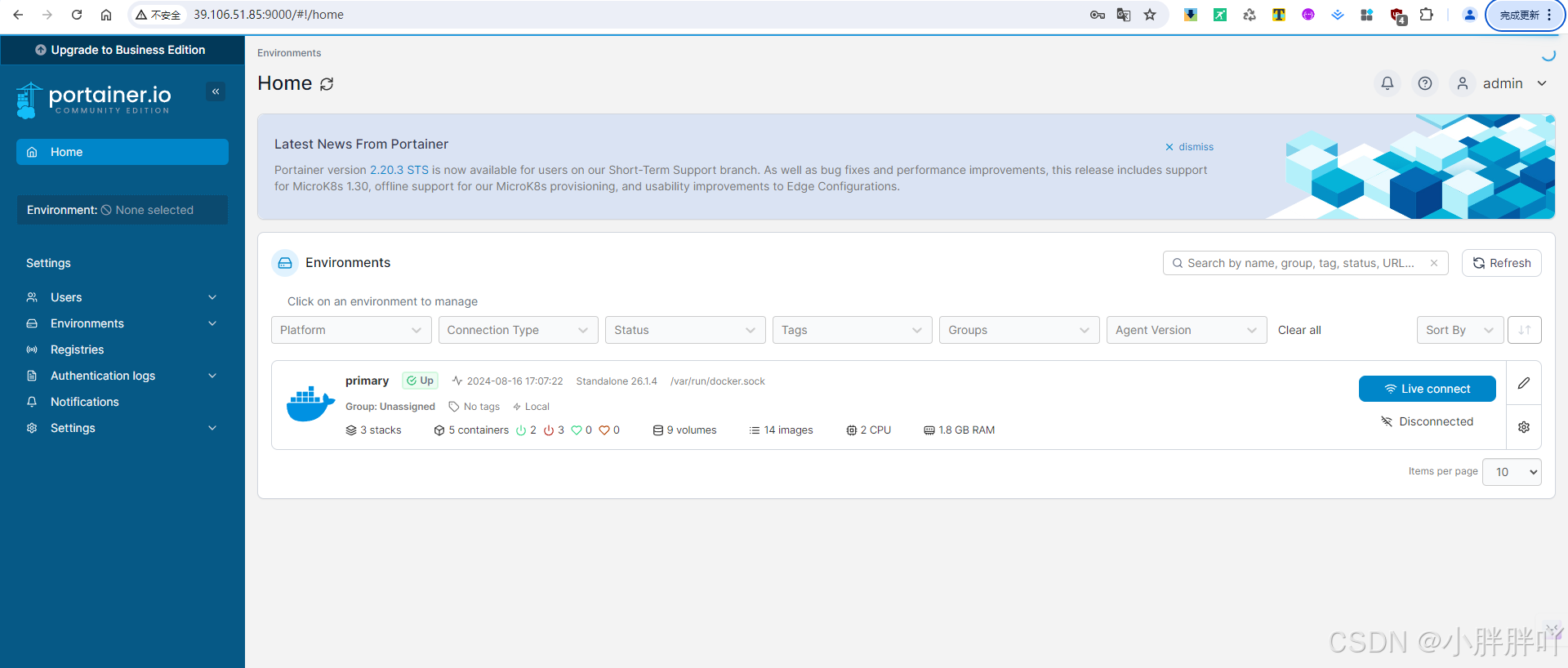
使用docker compose一键部署 Portainer Portainer 是一款轻量级的应用,它提供了图形化界面,用于方便地管理Docker环境,包括单机环境和集群环境。 1、创建安装目录 mkdir /data/partainer/ -p && cd /data/partainer2、创建docker…...

js原生模板引擎
在JavaScript中,可以使用模板字符串(template strings)来创建简单的模板。模板字符串是用反引号(`)标识的字符串,其中内嵌表达式使用${}格式。 下面是一个简单的模板函数示例,它接受一个对象作为参数,并使用模板字符串来生成一个HTML字符串。 function createTemplat…...

Java面试题———MySql篇③
目录 1.查询语句执行流程 2.索引的数据结构是什么 3.数据库中的锁有哪些 4.MySQL日志类型 5.MySQL主从复制的流程 6.谈谈你对sql的优化的经验 1.查询语句执行流程 一条查询语句到达MySQL数据库之后,数据库中的各个组件会按照顺序执行自己的任务 首先是连接器…...
ArcGis在线地图插件Maponline(好用版)
ArcGis加载插件,可在线浏览谷歌地图、天地图、高德地图、必应地图等多种,包含街道、影像、标注地图等信息(谷歌地图需自备上网手段),免费注册账号即可使用,可加载无水印底图。 与大地2000坐标无需配准直接使…...
Chainlit接入DifyAI知识库接口快速实现自定义用户聊天界面
前言 由于dify只提供了一个分享用的网页应用,网页访问地址没法自定义,虽然可以接入NextWeb/ChatGPT web/open webui等开源应用。但是如果我们想直接给客户应用,还需要客户去设置配置,里面还有很多我们不想展示给客户的东西怎么办…...
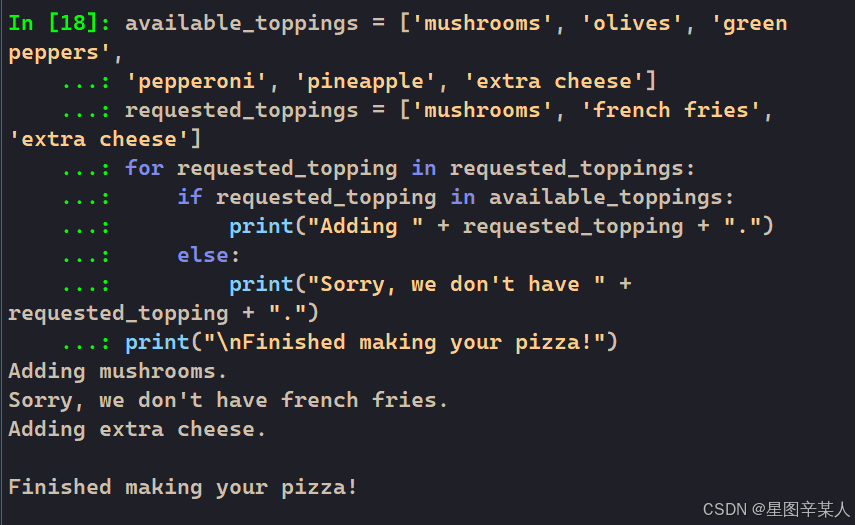
《Python编程:从入门到实践》笔记(一)
一、字符串 1.修改字符串大小写 title()以首字母大写的方式显示每个单词,即将每个单词的首字母都改为大写,其他的改为小写。 upper()将字母都改为大写,lower()将字母都改为小写。 2.合并(拼接)字符串 Python使用加号()来合并字符串。这种合…...
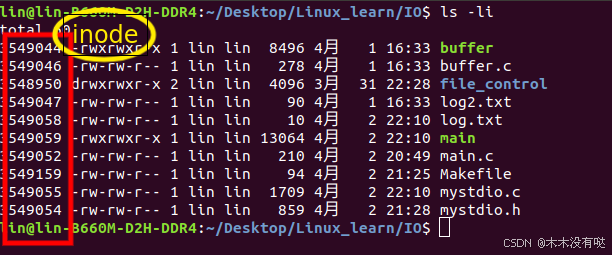
Linux入门——06 基础IO
1.什么是当前路径 exe -> /home/lin/Desktop/Linux_learn/fork_learn/test 当前进程执行是磁盘路径下的哪一个程序 cwd -> /home/lin/Desktop/Linux_learn/fork_learn 当前进程的工作目录------》当前进程 1.1当前路径这个地址能改吗? 可以,使…...

未来城市的科技展望
未来城市,将是科技与人文深度融合的产物,展现出一个全方位智能化、绿色生态且可持续发展的全新面貌。随着物联网、人工智能等技术的飞速发展,未来城市的轮廓逐渐清晰,它将为我们带来前所未有的生活体验。 在未来…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
