【前缀和算法】--- 一维和二维前缀和模板
Welcome to 9ilk's Code World

(๑•́ ₃ •̀๑) 个人主页: 9ilk
(๑•́ ₃ •̀๑) 文章专栏: 算法Journey
本文开始,博主开始讲解有关前缀和的算法,本篇博客我们先来了解一下有关前缀和的两个模板。
🏠 一维前缀和模板
📌 题目内容
一维前缀和
📌题目解析
- 数组的下标是从1开始的。
- 数组中每个值的范围是−10^9 ≤ a[i] ≤ 10^9,因此我们需要考虑如果多个值相加用int可能溢出,可以考虑用long long.
📌算法原理
✏️ 思路一:暴力解法
暴力解法很简单就是进行模拟,每次查询从L下标开始遍历直到到R下标。最坏情况是L是1下标,而R是n下标,n为数组长度。因此时间复杂度为O(q*n).
有没有什么优化的解法?
✏️ 思路二:前缀和
前缀和算tg法分为两步:1.预处理出来一个前缀和数组。2.使用前缀和数组。它可以用来快速求出数组中某一个连续区间的和。
-
预处理出前缀和数组

假设有一个数组arr,同时有个相关联的数组dp,dp[i]表示的是arr数组[1,i]区间内所有值和。
我们发现,比如dp[3]是【1,3】区间值的和,那么就相当于是【1,2】区间的和+arr[3].
因此我们可以得出公式dp[i] = dp[i-1] + arr[i].
通过公式我们在遍历一遍数组的同时,就可以求出前缀和数组。
-
使用前缀和数组

题目要我们求出[l,r]区间内值的和,由于我们提前求出了前缀和数组,我们发现所求区间 = 总和 - 前一段区间,因此【l,r】= dp[r] - dp[l-1],这个过程是很快的达到了O(1)。
参考代码:
typedef long long ll;
int main()
{int n = 0;int q = 0; //查询次数cin >> n >> q;vector<ll> v(n+1,0);vector<ll> dp(n+1,0);ll prev = 0;//获得前缀和数组//dp[i]表示的是从1到i区间值的总和for(int i = 1 ; i <= n ; i++){cin >> v[i];dp[i] = dp[i-1] + v[i];} //使用前缀和数组while(q--){int l = 0;int r = 0;cin >> l >> r;cout << dp[r] - dp[l-1] << endl; }return 0;
}-
细节问题
我们前缀和数组下标是从1开始的,如果下标从0开始,当求[0,2]区间的值之和时就转化成dp[2] - dp[-1]这个dp[-1]是个边界情况需要我们特殊处理且原本数组没有-1开始的;如果下标从1开始,当求[1,2]区间的值之和时转化成dp[2] - dp[0],对于dp[0]我们就容易将它处理为0即可。
总结:前缀和数组下标从1开始,是为了处理边界情况。
🏠 二维前缀和数组
📌 题目内容
二维前缀和
📌 题目解析
- 本题数据范围仍然过大,用int会有溢出的风险。
- 题目要我们求的是以(x1,y1)为左上角,(x2,y2)为右下角的子矩阵的和。
📌 算法原理
✏️ 思路一:暴力解法
暴力解法也就是模拟从第一个点开始直接按照划分区域进行遍历,最坏情况是整个矩阵,时间复杂度是O(n*m*q).
✏️ 思路二:二维前缀和
-
预处理出二维前缀和数组

假设有一个二维数组arr,dp数组是一个与它关联的数组。dp[i][j]表示以(1,1)为左上角,(i,j)为右上角形成的子矩阵中值之和。任取一块区域,假设D为(i,j)点,若我们要求dp[i][j]也就是求(1,1)到(i,j)区域的和,我们可以将这四部分相加,由于B和C不好求,我们可以利用A(dp[i-1][j-1])来间接求这两部分,但是不要忘记减去多进来的A。由于A+B和A+C在dp数组中分别对应的是dp[i-1][j]和dp[i][j-1],因此我们可以得到公式:
dp[ i ][ j ] = dp[ i-1 ][ j ] + dp[ i ][ j-1 ] + arr[ i ][ j ] - dp[ i-1][ j-1 ].
通过公式,我们在遍历二维数组时就可以求出对应的dp二维数组。
-
使用二维前缀和数组

题目要我们求以(x1,y1)为左上角,(x2,y2)为右上角区域的值之和,也就是求区域D。因此D可以由整体减去A,B,C三部分,由于B和C不好求,所以我们利用A间接求。于是有D=(A+B+C+D) - (A+C) - (A+B) +A。对于A就是dp[x1][y1],A+B就是dp[x1-1][y2],A+C就是dp[x2][y1-1],于是得到公式:D = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1]。此时 我们由于提前得到的二维前缀和数组,我们能很快得出D的值,时间复杂度是O(1).
时间复杂度优化为了O(m*n) + O(q).
参考代码:
int main()
{int n = 0; //行 int m = 0; //列int q = 0; //查询次数cin >> n >> m >> q;vector<vector<long long>> vv(n + 1);vector<vector<long long>> dp(n + 1);for (int i = 0; i <= n; i++){vv[i].resize(m + 1, 0);dp[i].resize(m + 1, 0);if (i >= 1){for (int j = 1; j <= m; j++){cin >> vv[i][j];}}}for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + vv[i][j] - dp[i-1][j-1];}}while (q--){int x1, x2, y1, y2 = 0;cin >> x1 >> y1 >> x2 >> y2;cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;}return 0;
}总结:
1. 一维和二维前缀和数组下标都是从1开始。
2.当我们需要快速求出一段连续区间或区域时,可以考虑用前缀和数组,用前缀和数组间接求我们需要的。
3.我们可以根据场景推导出公式获得前缀和数组。
相关文章:

【前缀和算法】--- 一维和二维前缀和模板
Welcome to 9ilks Code World (๑•́ ₃ •̀๑) 个人主页: 9ilk (๑•́ ₃ •̀๑) 文章专栏: 算法Journey 本文开始,博主开始讲解有关前缀和的算法,本篇博客我们先来了解一下有关前缀和的两个模板。 🏠 一维前缀和模板 &…...

有些信息注定会丢失
智能在分析问题、做出决策时,总是希望获取尽可能多的信息,以此更加准确地决策。然而,很遗憾的是,有一些信息注定会丢失,不可能获取完全的信息,而且即使能够获取,智能也不能完全利用。 这一点与…...

c#中Task.Run 和使用 Task 构造函数创建任务的区别
Task.Run 和使用 Task 构造函数创建任务是两种不同的方法,它们在某些方面有显著的区别: 启动方式: Task.Run 是一个静态方法,它立即启动一个任务并在后台执行指定的工作。它通常用于快速启动一个简单的后台任务。使用 Task 构造函数创建任务&…...

使用nginx做代理转发
需求1:通过监听服务器的80端口,将请求转发到另一台服务器的8070端口 打开nginx/nginx.conf文件 server {listen 80;server_name localhost;location /analys {proxy_pass http://10.xx.xx.xx:8070/;} }需求2:通过监听服务器的80端口&am…...

Java前端与后端交互:JSON与XML数据交换 - 掌握现代Web开发的核心技能
引言 随着互联网技术的不断进步,Web应用变得越来越复杂,从前端到后端的每一个环节都需要精心设计以保证良好的用户体验。在这个过程中,数据的传递扮演着至关重要的角色。无论是简单的表单提交还是复杂的API调用,都需要一种可靠的…...

网络攻击原理及过程
网络攻击原理表 攻击者 内容 攻击访问 攻击效果 攻击意图 黑客 挑战 间谍 用户命令 破坏信息 好奇 恐怖主义者 脚本或程序 本地访问 信息泄密 获取情报 公司职员 自治主体 远程访问 窃取服务 经济利益 职业犯罪分子 电磁泄露 拒绝服务 恐怖事…...
——ansible)
day30(8/16)——ansible
目录 一、回顾 1、mysql和python 1. mysql5.7 2. 可以使用pymysql非交互的管理mysql 2、mycat中间件 1. 独属于mysql主从的负载均衡策略 2.配置写主读从 3. 步骤 3.1 安装jdk 3.2 mycat 3.3 配置 3.4 启动和调试 二、运维自动化(ansible) 1、任务背…...

fastadmin 安装
环境要求,大家可以参考官方文档的,我这里使用的是phpstudy,很多已经集成了。 注意一点,PHP 版本:PHP 7.4 。 第二步:下载 下载地址:https://www.fastadmin.net/download.html 进入下载地址后…...

Unity动画模块 之 3D模型导入基础设置 Rig页签
本文仅作笔记学习和分享,不用做任何商业用途本文包括但不限于unity官方手册,unity唐老狮等教程知识,如有不足还请斧正 1.Rig页签 Rig 选项卡 - Unity 手册,rig是设置骨骼与替身系统的,工作流程如下 Avatar是什么…...

⭐️Python在Windows命令行(Command Prompt)运行Python脚本或交互式地执行Python代码详解
Python在Windows命令行(Command Prompt)运行Python脚本或交互式地执行Python代码详解 Python在Windows命令行(Command Prompt)运行Python脚本或交互式地执行Python代码详解一、安装Python二、运行Python脚本1. 打开命令行2. 导航到…...

Python | Leetcode Python题解之第355题设计推特
题目: 题解: class Twitter:class Node:def __init__(self):self.followee set()self.tweet list()def __init__(self):self.time 0self.recentMax 10self.tweetTime dict()self.user dict()def postTweet(self, userId: int, tweetId: int) ->…...

D. Beard Graph
https://codeforces.com/problemset/problem/165/D 主要是边转点 后面都是简单的线段树维护 我们维护ok标记,val值,黑(1),白(0) id.okl.ok&r.ok id.vall.valr.val 注意特判如果两个点一样是0,如果dfn[u]1>dfn[v]就不…...

使用预训练的 ONNX 格式的 YOLOv8n 模型进行目标检测,并在图像上绘制检测结果
目录 __init__方法: pre_process方法: run方法: filter_boxes方法: view_img方法: __init__方法: 初始化类的实例时,创建一个onnxruntime的推理会话,加载名为yolo…...

mac安装xmind
文章目录 介绍软件功能下载安装1.下载完成后打开downloads 双击进行安装2.将软件拖到应用程序中3.在启动台中搜索打开4.提示损坏问题解决5.执行完成关闭命令窗口6.打开成功,点击继续,跳过登录7.打开成功后,点击关于 小结 介绍 XMind 是一款流…...

MySQL分区表入门
MySQL数据库的分区表是一种将表数据分成逻辑上相关的部分并存储在不同的物理位置的技术。使用分区表可以提高查询性能、简化数据维护和提供更好的数据管理。 以下是MySQL中创建和使用分区表的一般步骤: 设计分区策略: 首先,需要确定如何将表…...
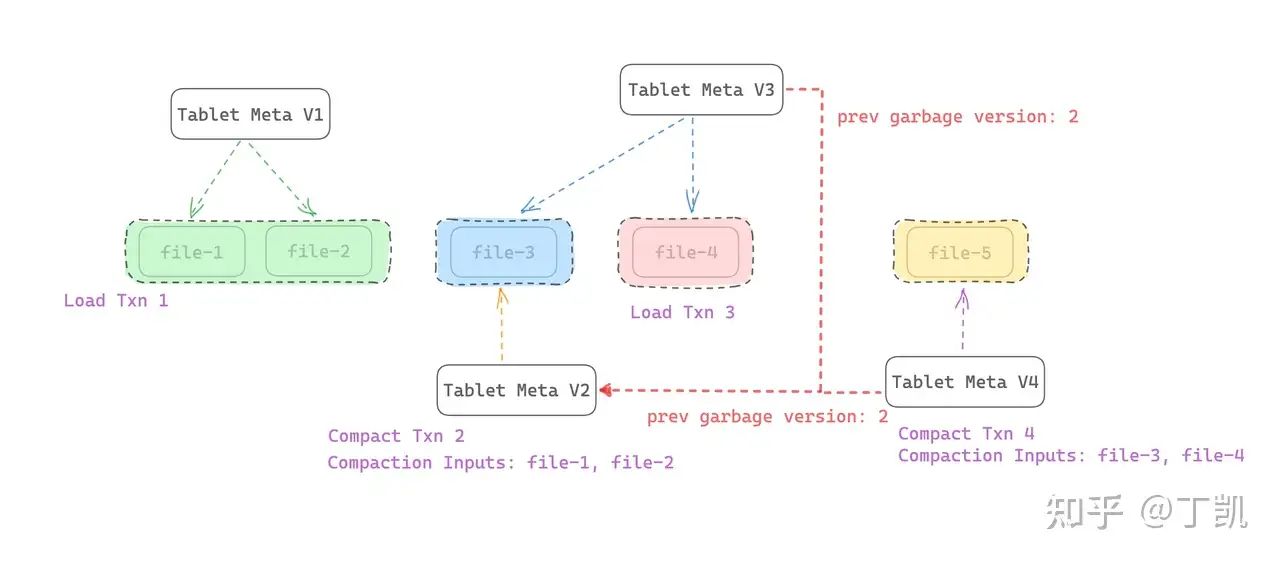
StarRocks 存算分离数据回收原理
前言 StarRocks存算分离表中,垃圾回收是为了删除那些无用的历史版本数据,从而节约存储空间。考虑到对象存储按照存储容量收费,因此,节约存储空间对于降本增效尤为必要。 在系统运行过程中,有以下几种情况可能会需要删…...

【运维】Linux中的xargs指令如何使用?
xargs 是 Linux 中一个非常强大的命令,用于将标准输入中的输出作为参数传递给其他命令。通常情况下,xargs 用于处理长列表或者将多行输入转换成一行。 以下是 xargs 的基本用法和一些常见的例子: 基本语法 command | xargs [options] [command]常见的例子 删除文件:假设…...

日志审计-graylog ssh登录超过6次告警
Apt 设备通过UDP收集日志,在gray创建接收端口192.168.0.187:1514 1、ssh登录失败次数大于5次 ssh日志级别默认为INFO级别,通过系统rsyslog模块处理,日志默认存储在/var/log/auth.log。 将日志转发到graylog vim /etc/rsyslog.conf 文件末…...

4. kafka消息监控客户端工具
KafkaKing官网地址 : https://github.com/Bronya0/Kafka-King github下载地址 : Releases Bronya0/Kafka-King (github.com) (windows、macos、linux版本) 云盘下载地址 : https://pan.baidu.com/s/1dzxTPYBcNjCTSsLuHc1TZw?pwd276i (仅windows版本) 连接kafka 输入本地地址…...

鸿蒙环境和模拟器安装
下载华为开发者工具套件,并解压 https://developer.harmonyos.com/deveco-developer-suite/enabling/kit?currentPage1&pageSize10 双击dmg安装ide 复制并解压sdk 安装模拟器 https://yuque.antfin-inc.com/ainan.lsd/cm586u/po19k1mi9b2728da?singleDoc#…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...


