算法:区间dp
文章目录
- 一、适用场景
- 二、基本思路
- 步骤
- 时间复杂度:
- 三、例题
区间动态规划(Interval DP)是一种用于解决某些需要处理区间或子段问题的动态规划方法,特别适合于问题的解可以通过子区间的解进行组合的情况。该方法的核心思想是在子区间上进行分治,将大问题划分为较小的子问题,通过解决这些子问题来构建整个问题的解。
一、适用场景
区间 DP 主要用于解决一些涉及区间(或序列)的问题。这类问题通常要求在一个序列上做某种操作(如合并、拆分、重排等),并且这些操作的结果取决于其子区间的操作结果。常见的应用包括:
- 石子合并问题(合并区间)。
- 括号匹配问题。
- 最优矩阵连乘问题。
- 回文分割问题。
二、基本思路
区间 DP 的核心是通过枚举区间的分割点,将问题分解为两个或多个子区间的问题。解决每个子区间的问题后,再通过这些子区间的解组合得到整个区间的解。
步骤
- 定义状态:
- 设
dp[i][j]表示在区间[i, j]上的最优解。
- 设
- 状态转移方程:
- 根据问题的性质,找到合适的分割方式,通常是选择一个分割点
k,将区间[i, j]分为[i, k]和[k+1, j]两个部分,并通过已知的子区间解来更新dp[i][j]。 - 一般形式的状态转移方程为:
d p [ i ] [ j ] = min i ≤ k < j ( d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + 合并代价 ) dp[i][j] = \min_{i \leq k < j} (dp[i][k] + dp[k+1][j] + 合并代价) dp[i][j]=i≤k<jmin(dp[i][k]+dp[k+1][j]+合并代价)
其中k是区间的分割点,合并代价由具体问题定义。
- 根据问题的性质,找到合适的分割方式,通常是选择一个分割点
- 初始状态:
- 最小区间的解(例如,当
i == j时,区间仅包含一个元素,通常可以直接得到最优解)。
- 最小区间的解(例如,当
- 结果:
- 最终目标是通过填充
dp数组,找到dp[1][n](即整个区间[1, n]的最优解)。
- 最终目标是通过填充
时间复杂度:
区间 DP 的时间复杂度取决于问题的规模。对于每个区间 [i, j],需要遍历所有的分割点 k,这通常需要三层循环,因此复杂度为 O ( n 3 ) O(n^3) O(n3),其中 n 是序列的长度。
三、例题
Acwing:282.石子合并

这是一个经典的区间dp的问题。根据前面的描述,我们可以知道,区间dp实际上就是将整个区间问题转化成多个区间子问题,然后状态转移至整个区间。
这里所说的石子合并,就是将两个子区间合并成一个大区间。
我们将石子合并成一堆,那么在前一步一定是两堆合并而来的,那么这两堆分别又是一个子问题,实际上动态规划也是处理子问题到整个问题转移的算法。
我们可以定义 d p [ i ] [ j ] dp[i][j] dp[i][j]表示从初始开始编号为i + 1 ~ j + 1的石子合并成一堆的最小代价。那么必然有 d p [ i ] [ j ] = d p [ i ] [ k ] + d p [ k + 1 ] [ j ] + m [ j ] − m [ i − 1 ] dp[i][j] = dp[i][k] + dp[k+1][j] +m[j] - m[i - 1] dp[i][j]=dp[i][k]+dp[k+1][j]+m[j]−m[i−1](其中i<=k<=j)。
我们可以发现,动态规划实际上就是带有记忆的搜素。这里我们并不知道哪个子问题合并起来才是最优的,因此我们遍历所有可能得子区间划分情况来求解。由这个递推,我们从小区间到大区间依次求值。
注意合并才有代价,单个石子代价为0。
时间复杂度: O ( N 3 ) O(N^3) O(N3)
#include<bits/stdc++.h>
using namespace std;
int main(void){ios_base::sync_with_stdio(false);cin.tie(0);int N; cin >> N;vector<int> m(N, 0);vector<vector<int>> dp(N, vector<int>(N, 0x3f3f3f3f));cin >> m[0]; dp[0][0] = 0;for(int i = 1; i < N; ++ i){cin >> m[i];m[i] += m[i - 1];dp[i][i] = 0;}for(int i = 1; i < N; ++ i){for(int j = 0; j + i < N; ++ j){int p = i + j;for(int k = j; k < p; ++ k){if(j != 0)dp[j][p] = min(dp[j][p], dp[j][k] + dp[k + 1][p] + m[p] - m[j - 1]);else dp[j][p] = min(dp[j][p], dp[j][k] + dp[k + 1][p] + m[p]);}}}cout << dp[0][N - 1];return 0;
}
相关文章:

算法:区间dp
文章目录 一、适用场景二、基本思路步骤时间复杂度: 三、例题 区间动态规划(Interval DP)是一种用于解决某些需要处理区间或子段问题的动态规划方法,特别适合于问题的解可以通过子区间的解进行组合的情况。该方法的核心思想是在子…...

【14.1运行版】C++俄罗斯方块-实现欢迎界面
实现欢迎界面 #include <stdio.h>//C语言形式的输入输出 #include <graphics.h>//图形库的头文件//实现欢迎界面 void welcome(void);int main(void) {welcome();//colsegraph();return 0; }void welcome(void) {//初始化画布initgraph(550, 660);//设置窗口标题H…...

数据分析:R语言计算XGBoost线性回归模型的SHAP值
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍SHAP用途计算方法:应用加载R包导入数据数据预处理函数模型介绍 SHAP(SHapley Additive exPlanations)值是一种解释机器学习模型预测的方法。它基于博弈论中的Shapley值概念,…...

SprinBoot+Vue图书馆预约与占座微信小程序的设计与实现
目录 1 项目介绍2 项目截图3 核心代码3.1 Controller3.2 Service3.3 Dao3.4 application.yml3.5 SpringbootApplication3.5 Vue3.6 uniapp代码 4 数据库表设计5 文档参考6 计算机毕设选题推荐7 源码获取 1 项目介绍 博主个人介绍:CSDN认证博客专家,CSDN平…...

云计算之大数据(上)
目录 一、Elasticsearch 1.1 产品组件 1.1.1 X-Pack 1.1.2 Beats数据采集中心 1.1.3 Logstash 1.1.4 Kibana 1.2 架构特性 1.2.1 性能 1.2.2 安全性 1.2.3 可用性 1.2.4 可扩展性 1.2.5 可维护性 1.2.6 国际化 1.3 综合检索分析 1.4 全观测 1.5 大数据检索加速…...

交友系统“陌陌”全方位解析
交友系统在现代社会中扮演着越来越重要的角色,尤其是随着互联网技术的发展,各种交友软件层出不穷。陌陌作为其中的佼佼者,其全方位解析对于理解交友系统的商业开发至关重要。 陌陌的核心功能是提供基于地理位置的社交服务,用户可…...

Android 删除开机动画
Android 删除开机动画 两种方法都是将debug.sf.nobootanimation的值改为属性1 第一种: frameworks/base/cmds/bootanimation/BootAnimationUtil.cpp bool bootAnimationDisabled() {char value[PROPERTY_VALUE_MAX]; // property_get("debug.sf.nobootani…...

我用 GPT 学占星
最近对占星赶兴趣,但是看到星盘中好多名词,不懂是什么意思?所以直接问 gpt , 发现回答的真的很棒🎉 ! 假如我想知道各个状态的具体是根据什么数据来显示的? 分分钟解决了我的问题; 我…...

028、架构_高可用_主从原理
MySQL半同步复制概览 MySQL主从复制是一个异步的复制过程,主库发送更新事件到从库,从库读取更新记录,并执行更新记录,使得从库的内容与主库保持一致。主从复制的基本过程如下图所示: 主从复制的完成通过以下三个进程实现的主库 binary log dump 线程:当从库连接主库时,…...

【启明智显技术分享】探讨CAN总线相关知识以及Model3C 2路CAN的应用
一、 CAN总线相关知识 CAN总线概述 CAN(Controller Area Network)总线是一种高实时性、高可靠性和灵活性的串行通信协议,广泛应用于汽车和工业控制系统中。它由德国BOSCH公司开发,最高速率可达到1Mbps,具有强大的检错…...

【python学习】深度解析 Python 的 .env配置与最佳实践:温格高的环境变量配置之道
1. 文章简介 在开发和部署 Python 项目时,环境变量配置对于管理敏感信息如数据库连接字符串、API 密钥至关重要。本文将以温格高(2023年环法冠军)的项目为例,详细介绍如何通过 .env 文件简化环境配置,并分享多环境管理、Docker 集成等热门功能。我们还将覆盖一些小技巧和…...
)
计算机考研真题知识点——2021(B)
目录 2021(B) 一、选择题 二、判断题 三、简答题 四、综合题 2021(B) 一、选择题 1、以下说法正确的是:C A、switch后面括号中放置的可以是值为任意类型的表达式。 B、continue和break均可以用在switch语句及循环语句中。 C、如果函数的返回类型与返回值类型不一…...

C#中ArrayList
ArrayList 1:位于System.Collections命名空间下, 2:ArrayList的容量可以根据需要自动扩充 3:只能是一维形式,数组可以是多维的 4:提供添加、删除、和插入某一范围元素的方法 三种构造方法 1) ArrayList list1 n…...

【MySQL】批量插入数据造数-存储过程
日常工作中可能有针对需要对某个表进行造数,如何批量插入呢? 可以使用存储过程循环结构。下面是一个存储过程以插入100条,while语句后的<控制循环次数。 concat是一个拼接语句,拼接后是test_1-100,这种也适用于ID/…...

基于Java+SpringBoot+Vue+MySQL的高校物品捐赠管理系统
作者:计算机学姐 开发技术:SpringBoot、SSM、Vue、MySQL、JSP、ElementUI等,“文末源码”。 专栏推荐:前后端分离项目源码、SpringBoot项目源码、SSM项目源码 系统展示 基于SpringBootVue的高校物品捐赠管理系统【附源码文档】、…...

UNION和UNION ALL的区别
一、区别 去重功能 UNION会去除结果集中的重复行。UNION ALL不会去除重复行,它只是简单地将多个结果集合并在一起。 性能 UNION ALL通常比UNION性能更好,因为UNION需要进行去重操作,这会增加额外的计算开销。 二、具体例子 假设有两个表tab…...

科研绘图系列:R语言PCoA图(PCoA plot)
文章目录 介绍PCoA图的作用:说明的问题:加载R包导入数据数据预处理画图参考介绍 PCoA(主坐标分析,Principal Coordinate Analysis)是一种多维数据的降维技术,它用于探索高维空间中样本之间的关系。PCoA通常用于生态学、遗传学和其他领域的数据分析,以揭示样本或个体之间…...
)
C++ 容器元素排序函数sort()
前言 std::sort()是C标准库提供了一个模板函数,这个函数用于对给定范围内的元素进行排序,默认情况下,它使用元素类型的 < 操作符来确定元素的顺序。如果元素类型不支持 < 操作符,或者你需要按照不同于 < 的顺序来排序&a…...
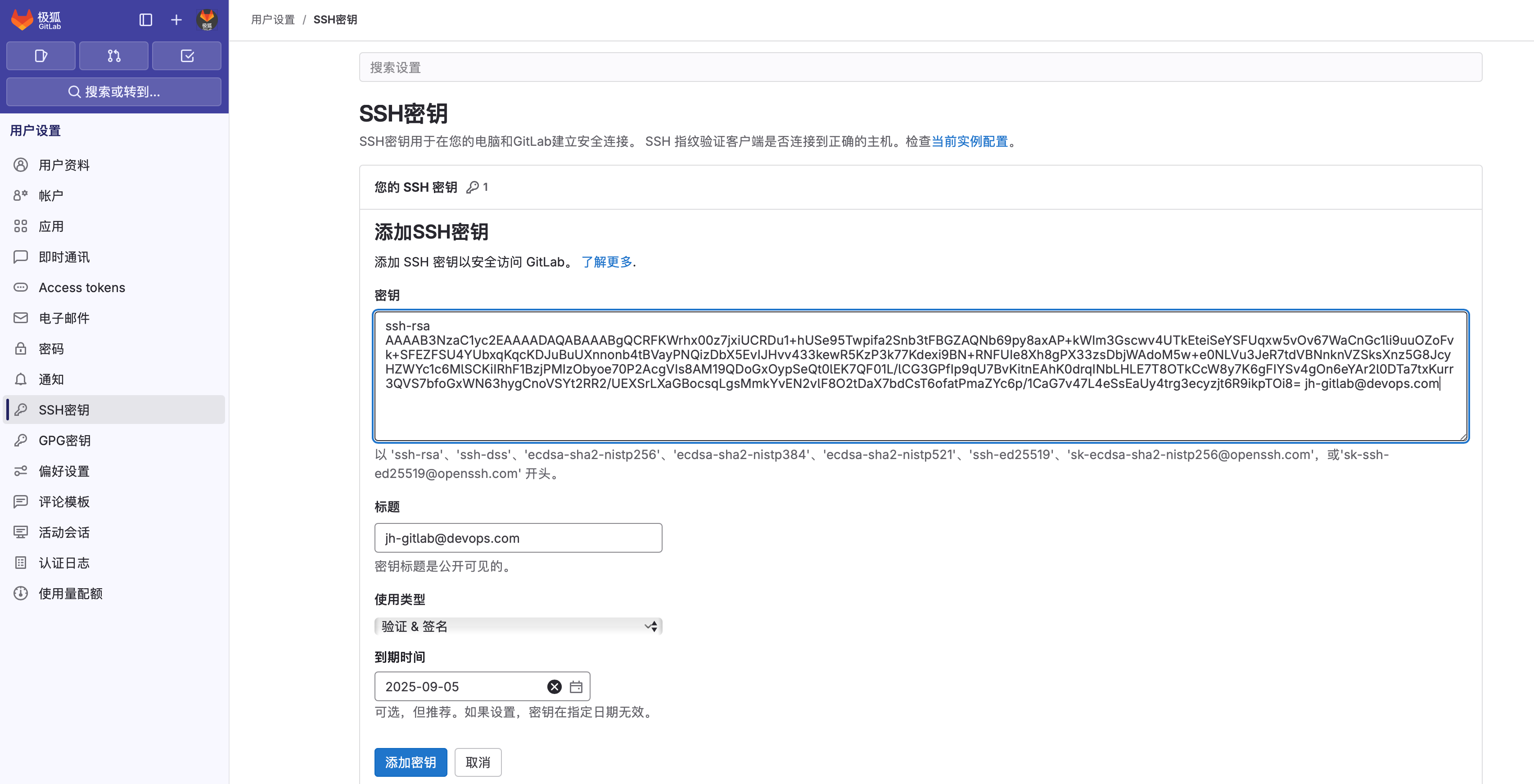
如何在极狐GitLab中添加 SSH Key?
本文分享如何生成 SSH Key 并添加到极狐GitLab 中,然后用 SSH Key 进行代码拉取。 极狐GitLab 是 GitLab 在中国的发行版,可以私有化部署,对中文的支持非常友好,是专为中国程序员和企业推出的企业级一体化 DevOps 平台࿰…...

Kafka-设计原理
ControllerLeader - PartitionRebalance消息发布机制HW与LEO日志分段 Controller Kafka核心总控制器Controller:在Kafka集群中会有一个或者多个broker,其中有一个broker会被选举为控制器(Kafka Controller),它负责管理…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...

Python 高效图像帧提取与视频编码:实战指南
Python 高效图像帧提取与视频编码:实战指南 在音视频处理领域,图像帧提取与视频编码是基础但极具挑战性的任务。Python 结合强大的第三方库(如 OpenCV、FFmpeg、PyAV),可以高效处理视频流,实现快速帧提取、压缩编码等关键功能。本文将深入介绍如何优化这些流程,提高处理…...
