当前位置： 首页 > news >正文

1990-2022年各地级市gdp、一二三产业gdp及人均gdp数据

news 2026/2/10 3:04:26

1990-2022年各地级市gdp、一二三产业gdp及人均gdp数据

1、时间：1990-2022年

2、来源：城市统计年鉴

3、指标：年度、城市名称、城市代码、城市类别、省份标识、省份名称、国内生产总值/亿元、第一产业占GDP比重(%)、第二产业占GDP比重(%)、第三产业占GDP比重(%)、人均地区生产总值/元、地区生产总值同比/%、第一产业生产总值/万元、第二产业生产总值/万元、第三产业生产总值/万元

4、范围：地级市

5、缺失情况：参看链接内数据预览
链接: https://pan.baidu.com/s/126fu0btJtu32pLBMSn6kew

提取码: 7yty 

6、下载链接：

1990-2022年各地级市GDP、一二三产业GDP及人均GDP数据icon-default.png?t=O83Ahttps://download.csdn.net/download/m0_71334485/89716492

相关文章：

1990-2022年各地级市gdp、一二三产业gdp及人均gdp数据

1990-2022年各地级市gdp、一二三产业gdp及人均gdp数据 1、时间：1990-2022年 2、来源：城市统计年鉴 3、指标：年度、城市名称、城市代码、城市类别、省份标识、省份名称、国内生产总值/亿元、第一产业占GDP比重(%)、第二产业占GDP比重(%)、第…...

编程日记 2024/9/6 17:33:19

c++ 原型模式

文章目录 什么是原型模式为什么要使用原型模式使用场景示例 什么是原型模式 用原型实例指定创建对象的种类，并通过拷贝这些原型创建新的对象，简单理解就是“克隆指定对象” 为什么要使用原型模式 原型模式（Prototype Pattern）是…...

编程日记 2024/9/6 17:30:15

论tomcat线程池和spring封装的线程池

Tomcat 中的线程池是什么？ 内部线程池：Tomcat 确实有一个内部的线程池，用于处理 HTTP 请求，通常是org.apache.tomcat.util.threads.ThreadPoolExecutor 类的实例。这个线程池专门用于处理进入的 HTTP 请求和发送响应。可以通过 T…...

编程日记 2024/9/6 17:29:14

阿里P7大牛整理自动化测试高频面试题

最近好多粉丝咨询我，有没有软件测试方面的面试题，尤其是Python自动化测试相关的最新面试题，所以今天给大家整理了一份，希望能帮助到你们。 接口测试基础 1、公司接口测试流程是什么？ 从开发那边获取接口设计文档、分…...

编程日记 2024/9/6 17:27:13

vue如何实现路由缓存

&#xff08;以下示例皆是以vue3vitets项目为例&#xff09; 场景一&#xff1a;所有路由都可以进行缓存 在渲染路由视图对应的页面进行缓存设置&#xff0c;代码如下&#xff1a; <template><router-view v-slot"{ Component, route }"><transiti…...

编程日记 2024/9/6 17:25:11

基于Openjdk容器打包运行jar程序

文章目录 应用场景基于Openjdk容器打包运行jar程序1.编译项目成jar包2.构建Dockerfile文件精简版-含jar包精简版-不含jar包带注释版-含jar包 3.编译Dockerfile成镜像。4.运行镜像&#xff1a; 应用场景 部署多版本jdk的应用程序。 基于Openjdk容器打包运行jar程序 1.编译项目…...

编程日记 2024/9/6 17:24:11

DNN学习平台（GoogleNet、SSD、FastRCNN、Yolov3）

DNN学习平台&#xff08;GoogleNet、SSD、FastRCNN、Yolov3&#xff09; 前言相关介绍1&#xff0c;登录界面&#xff1a;2&#xff0c;主界面&#xff1a;3&#xff0c;部分功能演示如下&#xff08;1&#xff09;识别网络图片&#xff08;2&#xff09;GoogleNet分类&#xf…...

编程日记 2024/9/6 17:22:09

HTTP协议(超文本传输协议)

HTTP请求消息 http请求消息组成&#xff1a; 请求行 &#xff1a;包含请求的方法 操作资源的地址 协议的版本号 http请求方法&#xff1a; GET&#xff1a;从服务器获取资源 POST&#xff1a;添加资源信息 PUT&#xff1a;请求服务器更新资源信息 DELETE&#xff1a;请…...

编程日记 2024/9/6 17:20:07

FFmpeg的日志系统（ubuntu 环境）

1. 新建.c文件 vim ffmpeg_log.c2. 输入文本 #include<stdio.h> #include<libavutil/log.h> int main() {av_log_set_level(AV_LOG_DEBUG);av_log(NULL,AV_LOG_INFO,"hello world");return 0; }当log level < AV_LOG_DEBUG 都可以印出来 #define A…...

编程日记 2024/9/6 17:19:07

浅析VO、DTO、DO、PO

一、概念介绍 POJO&#xff08;plain ordinary java object&#xff09; &#xff1a; 简单java对象&#xff0c;个人感觉POJO是最常见最多变的对象&#xff0c;是一个中间对象&#xff0c;也是我们最常打交道的对象。一个POJO持久化以后就是PO&#xff0c;直接用它传递、传递…...

编程日记 2024/9/6 17:18:05

android kotlin基础复习 enum

1、kotlin中&#xff0c;关键字enum来定义枚举类型。枚举类型可以包含多个枚举常量&#xff0c;并且每个枚举常量可以有自己的属性和方法。 2、测试代码&#xff1a; enum class Color{RED,YELLOW,BLACK,GOLD,BLUE,GREEN,WHITE }inline fun <reified T : Enum<T>>…...

编程日记 2024/9/6 17:17:04

个股场外期权怎么交易？场外期权交易流程是怎样的？

今天带你了解个股场外期权怎么交易&#xff1f;场外期权交易流程是怎样的&#xff1f;个股场外期权是一种非标准化的期权合约&#xff0c;通常在场外市场&#xff08;OTC市场&#xff09;由金融机构和投资者之间进行交易。 场外个股期权主要功能 风险管理&#xff1a; 帮助投…...

编程日记 2024/9/6 17:16:03

企业选ETL还是ELT架构？

作为数据处理的重要工具&#xff0c;ETL工具被广泛使用&#xff0c;同时ETL也是数据仓库中的重要环节。本文将从解释ETL工具是怎么处理数据&#xff0c;同时介绍ELT和ETL工具在企业搭建数据仓库的重要优势。 一、什么是ETL? ETL是Extract-Transform-Load的缩写&#xff0c;将…...

编程日记 2024/9/6 17:13:00

【Spring Boot 3】【Web】同时启用 HTTP 和 HTTPS

【Spring Boot 3】【Web】同时启用 HTTP 和 HTTPS 背景介绍开发环境开发步骤及源码工程目录结构背景 软件开发是一门实践性科学，对大多数人来说，学习一种新技术不是一开始就去深究其原理，而是先从做出一个可工作的DEMO入手。但在我个人学习和工作经历中，每次学习新技术总是…...

编程日记 2024/9/6 17:11:59

【Android】最好用的网络库：Retrofit

最好用的网络库&#xff1a;Retrofit 文章目录 最好用的网络库&#xff1a;RetrofitRetrofit的基本用法Retrofit的使用逻辑Retrofit的基本操作处理复杂的接口地址类型进阶删除提交header中指定参数 Retrofit构建器的最佳写法Retrofit的使用封装 用户网络请求的接口配置繁琐&…...

编程日记 2024/9/6 17:10:58

SpringBoot自动化配置原理

SpringBoot自动化配置原理 01-SpringBoot2高级-starter依赖管理机制 目的&#xff1a;通过依赖能了解SpringBoot管理了哪些starter 讲解&#xff1a; 通过依赖 spring-boot-dependencies 搜索 starter- 发现非常多的官方starter&#xff0c;并且已经帮助我们管理好了版本。 …...

编程日记 2024/9/6 17:06:55

2024级新生数组字符串专题题解

一、题解&#xff1a; 1.A-[NOIP2005]校门外的树_24级新生数组字符串训练题 (nowcoder.com) 这题常见的解法有两种&#xff1a; 第一种是这道题我们可以直接按照题目意思枚举 #include<bits/stdc.h> #define int long long using namespace std;int road[10010];sig…...

编程日记 2024/9/6 17:05:54

C++学习 虚函数，容器

一、虚函数 虚函数是C中的一种函数&#xff0c;允许子类重写父类中的函数&#xff0c;以便在运行时通过基类指针或引用调用子类的函数实现。虚函数的主要作用是实现多态性&#xff0c;这使得基类指针或引用可以根据实际指向的对象类型调用不同的函数实现。具体用法 虚函数的声…...

编程日记 2024/9/6 17:04:53

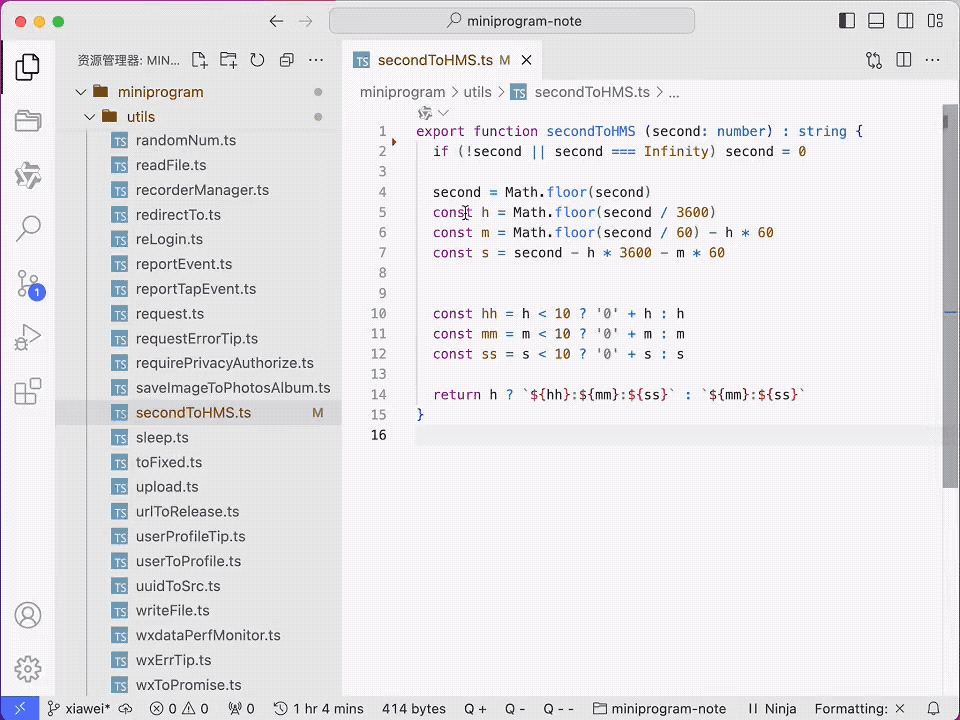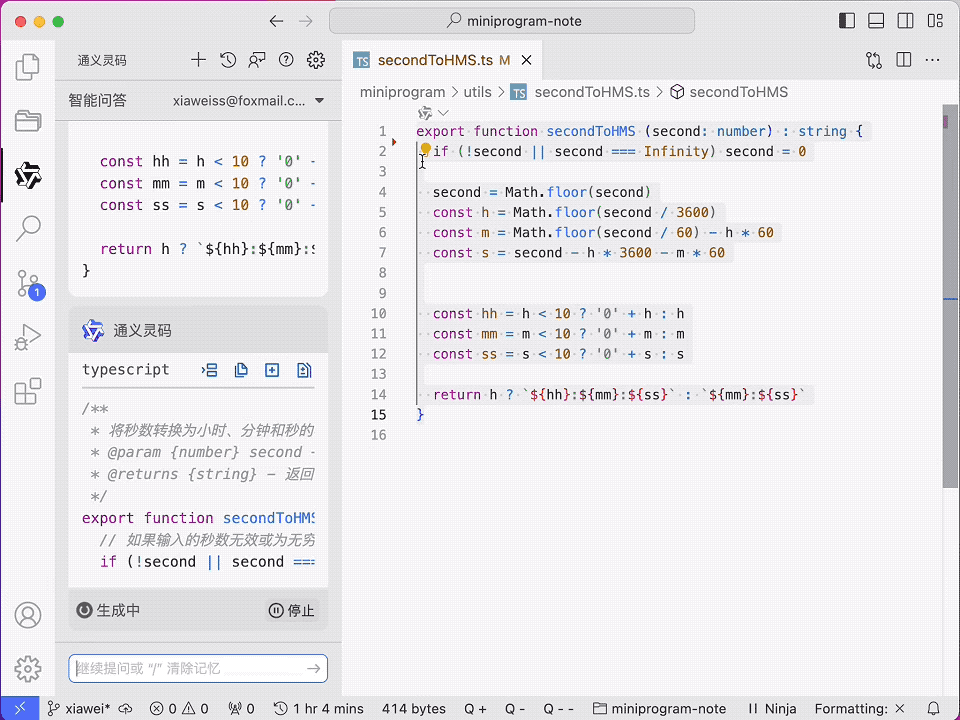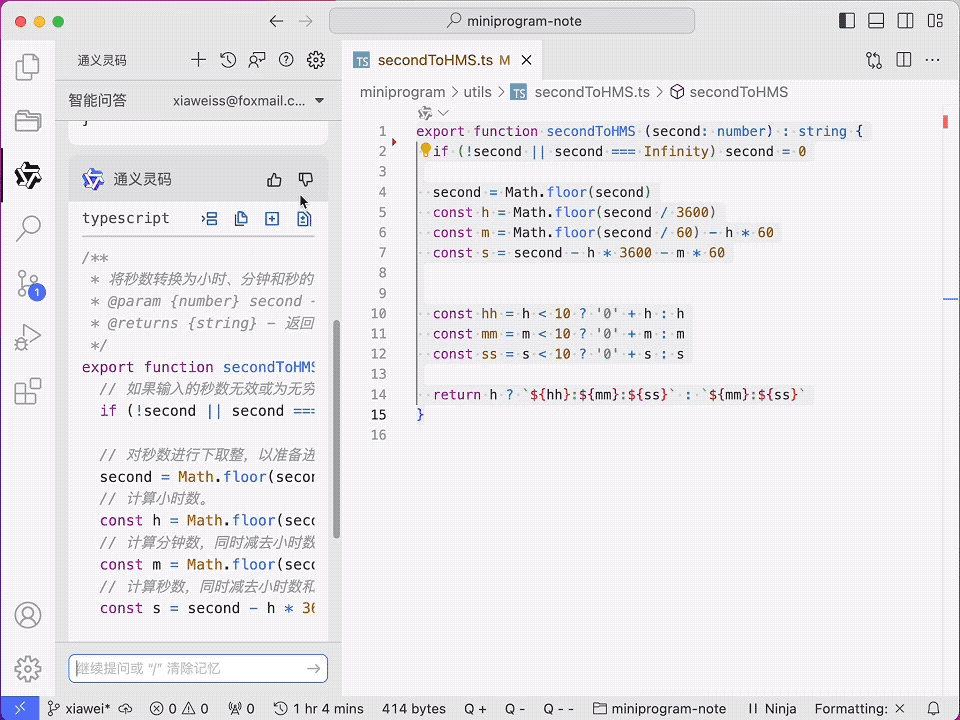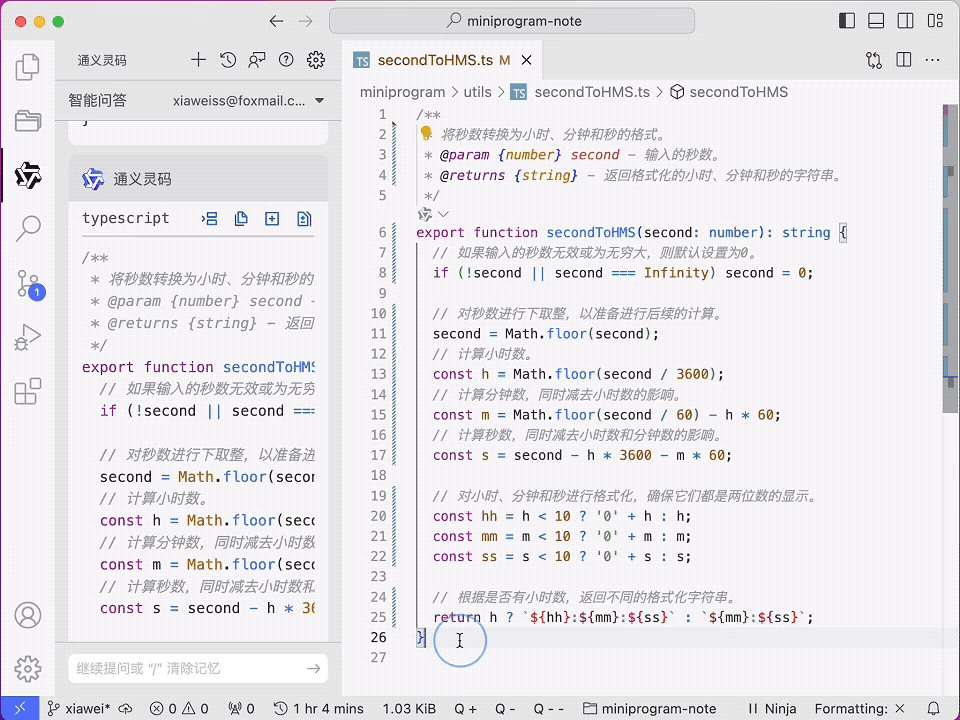
MacTalk 测评通义灵码，如何实现“微信表情”小功能？

作者&#xff1a;池建强&#xff0c;墨问西东创始人 前段时间&#xff0c;我写了篇墨问研发团队放弃 GitHub Copilot 的文章&#xff0c;没想到留言区一些读者推荐我们试试通义灵码&#xff0c;说它效果很不错。我呢&#xff0c;一直没腾出时间折腾。 直到月中时&#xff0c;…...

编程日记 2024/9/6 17:01:50

Canvas Confetti - 免费开源的五彩纸屑飞舞特效的 JS 库，多用于在网页上实现欢乐庆祝的场景

今天看科技周刊看到的一个酷炫的动效库&#xff0c;使用简单&#xff0c;视觉效果很好&#xff0c;推荐给大家。 Canvas Confetti 是一个基于 JavaScript 的特效动画库&#xff0c;可以在网页界面上轻松地实现五彩纸屑飞舞的庆祝场景特效。这个特效库封装了几种酷炫的特效&…...

编程日记 2024/9/6 16:59:48

JVM垃圾回收机制全解析

Java虚拟机&#xff08;JVM&#xff09;中的垃圾收集器&#xff08;Garbage Collector&#xff0c;简称GC&#xff09;是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象&#xff0c;从而释放内存空间&#xff0c;避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

编程新知 2026/1/9 14:53:35

【SQL学习笔记1】增删改查+多表连接全解析（内附SQL免费在线练习工具）

可以使用Sqliteviz这个网站免费编写sql语句&#xff0c;它能够让用户直接在浏览器内练习SQL的语法&#xff0c;不需要安装任何软件。 链接如下&#xff1a; sqliteviz 注意&#xff1a; 在转写SQL语法时&#xff0c;关键字之间有一个特定的顺序&#xff0c;这个顺序会影响到…...

编程新知 2026/2/5 4:36:53

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测；从基础到高级，涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等

&#x1f50d; 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术&#xff0c;可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势&#xff0c;还能有效评价重大生态工程…...

编程新知 2025/9/12 15:10:44

【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张（Windows/Linux）

要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况&#xff0c;可以通过以下几种方式模拟或触发&#xff1a; 1. 增加CPU负载 运行大量计算密集型任务&#xff0c;例如&#xff1a; 使用多线程循环执行复杂计算&#xff08;如数学运算、加密解密等&#xff09;。运行图…...

编程新知 2025/11/30 10:30:15

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/10/13 2:26:14

Linux --进程控制

本文从以下五个方面来初步认识进程控制&#xff1a; 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程&#xff0c;创建出来的进程就是子进程&#xff0c;原来的进程为父进程。…...

编程新知 2026/1/30 15:27:25

JAVA后端开发——多租户

数据隔离是多租户系统中的核心概念&#xff0c;确保一个租户&#xff08;在这个系统中可能是一个公司或一个独立的客户&#xff09;的数据对其他租户是不可见的。在 RuoYi 框架&#xff08;您当前项目所使用的基础框架&#xff09;中&#xff0c;这通常是通过在数据表中增加一个…...

编程新知 2025/12/18 8:35:12

处理vxe-table 表尾数据是单独一个接口，表格tableData数据更新后，需要点击两下，表尾才是正确的

修改bug思路&#xff1a; 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑&#xff1a;async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

编程新知 2026/1/25 6:16:49

全面解析数据库：从基础概念到前沿应用​

在数字化时代&#xff0c;数据已成为企业和社会发展的核心资产&#xff0c;而数据库作为存储、管理和处理数据的关键工具&#xff0c;在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理&#xff0c;到社交网络的用户数据存储&#xff0c;再到金融行业的交易记录处理&a…...

编程新知 2025/9/19 11:48:17

GAN模式奔溃的探讨论文综述（一）

简介 简介：今天带来一篇关于GAN的，对于模式奔溃的一个探讨的一个问题，帮助大家更好的解决训练中遇到的一个难题。 论文题目：An in-depth review and analysis of mode collapse in GAN 期刊：Machine Learning 链接：...

编程新知 2026/2/8 17:40:01