常用算法实现【必会】:sort/bfs/dfs
文章目录
- 常用排序算法实现(Go版本)
- BFS 广度优先遍历,利用queue
- DFS 深度优先遍历,利用stack
- 前序遍历(根 左 右)
- 中序遍历(左根右)
- 后序遍历(左 右 根)
- BFS/DFS 总结
常用排序算法实现(Go版本)
// 快排(分治)
// 时间复杂度:O(nlogn) 空间复杂度:O(logn)
func QuickSort(arr []int, left, right int) {var QuickSorting = func(arr []int, left, right int) int {tmp := arr[right] // 1、从右向左依次选基准值tmpfor left < right {for arr[left] <= tmp && left < right { // 2、每轮循环中先从左向右,遇到比基准值小的数则left++left++}if left < right {arr[right] = arr[left] // 3、直至遇到比基准值大的数x=array[left]为止,然后再交换基准值与较大值x的位置(保证基准值左侧的值都比基准值tmp小)}for arr[right] >= tmp && left < right { // 4、每轮循环中再从右向左,遇到比基准值大的数则right--right--}if left < right { // 5、直至遇到比基准值小的数y=array[right]为止,然后再交换基准值与较小值y的位置(保证基准值右侧的值都比基准值tmp大)arr[left] = arr[right]}}arr[left] = tmpreturn left}if left < right {mid := QuickSorting(arr, left, right)QuickSort(arr, left, mid-1)QuickSort(arr, mid+1, right)}
}// 快排(非递归)// todo:待补充
// https://www.bilibili.com/video/av758822583/?vd_source=2c268e25ffa1022b703ae0349e3659e4
func QuickSortNotByRecursion(arr []int) {
}// 堆排(大顶堆:每个节点的值都大于或等于其左右孩子节点的值)
// 时间复杂度:O(nlogn) 空间复杂度:O(1)
func HeapSort(arr []int) {var CreateHeap = func(arr []int, i, length int) {tmp := arr[i]// 注意for循环条件:是 j<length 而不是 j<len(arr)for j := 2*i + 1; j < length; j = j*2 + 1 { // j=2i+1:当前根节点的左孩子下标 j= 2*j + 1:以当前叶子节点为新根节点,该新根节点的下一层叶子节点左孩子下标if j+1 < length && arr[j] < arr[j+1] { // j+1<length:右孩子(j+1)不能超出len长度范围j++}if tmp > arr[j] { // 左右孩子节点中选较大的节点值,并与父节点比较大小break // 若父节点值满足"大于或等于其左右孩子节点的值"则break,否则与较大的孩子节点相互交换}arr[i] = arr[j]i = j}arr[i] = tmp // 将最终比较后较小值放到合适的位置}// 首次构建堆l := len(arr)for i := l / 2; i >= 0; i-- { // 从二叉树最后一个父节点从底向上遍历(最上面的父节点:i = 0;最后一个父节点下标:i = len(arr) / 2)CreateHeap(arr, i, l)}// 再次重建堆for i := l - 1; i > 0; i-- { // 从下往上不断在每轮循环中置换出当前最大值,arr长度i也逐渐减到0arr[0], arr[i] = arr[i], arr[0] // swap 把大顶堆根节点(下标为0)上的最大值交换到末尾,置换出来.CreateHeap(arr, 0, i)}
}// 归并
// 时间复杂度:O(nlogn) 空间复杂度:O(n)
func MergeSort(arr []int, length int) {var MergeSorting = func(arr1, arr2 []int, length1, length2 int) {i, j := 0, 0tempArr := make([]int, 0 /*, length1+length2*/)// 1.分别将两个子数组中较小一方的值按大小顺序移动到临时数组tempArr中for i < length1 && j < length2 {if arr1[i] < arr2[j] {tempArr = append(tempArr, arr1[i]) // 将较小值加入临时数组tempArri++// fmt.Println("i ", i)} else {tempArr = append(tempArr, arr2[j])j++// fmt.Println("j ", j)}}// 2.肯定存在一个子数组先移动完,所以需要将另一个未移动完的有序子数组剩下的元素继续移动到tempArr中if i < length1 {tmpArr = append(tmpArr, arr1[i:]...)}if j < length2 {tmpArr = append(tmpArr, arr2[j:]...)}// 3.将合并数组值赋给原始数组copy(arr, tmpArr) // arr = tempArr // 此赋值方式不会影响main()中原数组arr中的值,仅仅在该函数作用域内的结果是排好序的// for i := 0; i < length1+length2; i++ {// arr[i] = tmpArr[i]// }}// 注意:下面的l1和l2不能写成 "len(arr)/2" 和 "len(arr)-l1"if length > 1 { // 最后拆至每个子数组只有一个元素l1 := length / 2l2 := length - l1arr1, arr2 := arr, arr[l1:] // arr1原数组前半部分、arr2原数组后半部分MergeSort(arr1, l1) // 不断拆分数组长度直至长度为1MergeSort(arr2, l2) // 不断拆分数组长度直至长度为1MergeSorting(arr1, arr2, l1, l2)// mid := length / 2// arr1, arr2 := arr[:mid], arr[mid:] // arr1原数组前半部分、arr2原数组后半部分// MergeSort(arr1, len(arr1)) // 不断拆分数组长度直至长度为1// MergeSort(arr2, len(arr2)) // 不断拆分数组长度直至长度为1// MergeSorting(arr1, arr2, len(arr1), len(arr2))}
}// 冒泡
// 时间复杂度:O(n^2) 空间复杂度:O(1)
func MaoPaoSort(arr []int) {for i := 0; i < len(arr); i++ {for j := i + 1; j < len(arr); j++ {if arr[i] > arr[j] {arr[i], arr[j] = arr[j], arr[i] // swap}}}
}func main() {array := []int{5, 28, 73, 19, 6, 0, 5}// MaoPaoSort(array)// QuickSort(array, 0, len(array)-1)// QuickSortNotByRecursion(array)// HeapSort(array)MergeSort(array, len(array))fmt.Println(array)return
}
BFS 广度优先遍历,利用queue
// BFS(利用队列:尾进头出)
func levelOrder(root *TreeNode) []int {res := make([]int, 0)if root == nil { return res}queue := []*TreeNode{root} // 开始循环前,先塞入rootfor len(queue) > 0 {root = queue[0] // 获取即将出队的头节点res = append(res, root.Val)queue = queue[1:] // 头结点出队if root.Left != nil {queue = append(queue, root.Left)}if root.Right != nil {queue = append(queue, root.Right)}}return res
}
DFS 深度优先遍历,利用stack
前序遍历(根 左 右)
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
// 迭代
func preorderTraversal(root *TreeNode) []int {array := make([]int, 0)stack := make([]*TreeNode, 0)for root != nil || len(stack) > 0 {// 不断遍历左子树for root != nil {array = append(array, root.Val) // result, finally return stack = append(stack, root) // pushroot = root.Left}// 左子树遍历完了,开始从下往上遍历右子树(每次找栈顶指针,然后pop出栈)if len(stack) > 0 {root = stack[len(stack) - 1] // 获取栈顶元素root = root.Rightstack = stack[: len(stack) - 1] // pop}}return array
}// 递归
var array []int
func preorderTraversal(root *TreeNode) []int {array = make([]int, 0)dfs(root)return array
}func dfs(root *TreeNode) {if root == nil {return}array = append(array, root.Val)dfs(root.Left)dfs(root.Right)
}
中序遍历(左根右)
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/// 迭代
func inorderTraversal(root *TreeNode) []int {res := make([]int, 0)stack := make([]*TreeNode, 0)for root != nil || len(stack) > 0 {for root != nil {stack = append(stack, root)root = root.Left}if len(stack) > 0 {top := stack[len(stack) - 1]res = append(res, top.Val)root = top.Rightstack = stack[:len(stack) - 1] // pop}}return res
}// 递归
func inorderTraversal(root *TreeNode) []int {res := make([]int, 0)var inorder func(root *TreeNode)inorder = func(root *TreeNode) {if root != nil {inorder(root.Left)res = append(res, root.Val)inorder(root.Right)}}inorder(root)return res
}
后序遍历(左 右 根)
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/// 迭代
// https://github.com/HelloWorld-666/C_Tree/blob/master/C_Tree/main.cpp
// 每个节点会经过两次栈,第一次不断遍历左子节点会经过,第二次遍历完右子节点后,获取栈顶节点时也会经过;
// 且当某个根节点root左右孩子节点都为空时,root出栈并置空
func postorderTraversal(root *TreeNode) []int {res := make([]int, 0)stack:= make([]*TreeNode, 0)flagMap := make(map[*TreeNode]int) // 标记节点是第几次经过根节点 => 入栈for root != nil || len(stack) > 0 {for root != nil { // 遍历左子节点stack = append(stack, root) // pushflagMap[root] = 1 // 第1次经过该节点时,做标记:1root = root.Left}if len(stack) > 0 {root = stack[len(stack) - 1] // 获取栈顶节点if flagMap[root] == 1 {flagMap[root] = 2 // 第2次经过该节点时,做标记:2root = root.Right} else {res = append(res, root.Val)stack = stack[:len(stack) - 1] // pop stack top noderoot = nil // 当前root的左右子节点都为空时(叶子节点),将该root出栈且置空,避免该root因不等于空而再次进入上方内循环中逻辑.}}}return res
}// 递归
func postorderTraversal(root *TreeNode) []int {res := make([]int, 0)var recursion func(root *TreeNode)recursion = func(root *TreeNode) {if root != nil {recursion(root.Left)recursion(root.Right)res = append(res, root.Val)}}recursion(root)return res
}
BFS/DFS 总结
将所有结点都看作根结点,关键在于何时访问。
前序:入栈时访问;中序:第一次退栈时访问;后序:第二次退栈时访问。
深度优先遍历(借助栈stack结构来实现) = 前中后序遍历
dfs:一条路走的死,用栈实现,进栈、退栈,一搜到底!一般用 递归 实现
bfs: 辐射八方,用队实现,入队、出队,步步为营!一般用 迭代 实现
深度优先,就是 一条路走到底,广度优先,就是 每条路都同时派人走 。
另外:删除一棵二叉树,即释放一棵二叉树的内存,用后序遍历即可实现(这里的“访问”变成了delete 结点).
相关文章:

常用算法实现【必会】:sort/bfs/dfs
文章目录常用排序算法实现(Go版本)BFS 广度优先遍历,利用queueDFS 深度优先遍历,利用stack前序遍历(根 左 右)中序遍历(左根右)后序遍历(左 右 根)BFS/DFS 总…...
瑟瑟发抖吧——用了这款软件,我的开发效率提升了50%
一、前言 开发中,一直听到有人讨论是否需要重复造轮子,我觉得有能力的人,轮子得造。但是往往开发周期短,用轮子所节省的时间去更好的理解业务,应用到业务中,也能清晰发现轮子的利弊,一定意义上…...
笔记本只使用Linux是什么体验?
个人主页:董哥聊技术我是董哥,嵌入式领域新星创作者创作理念:专注分享高质量嵌入式文章,让大家读有所得!近期,也有朋友问我,笔记本只安装Linux怎么样,刚好我也借此来表达一下我的感受…...

pipeline业务发布
业务环境介绍公司当前业务上线流程首先是通过nginx灰度,dubbo-admin操作禁用,然后发布上线主机,发布成功后,dubbo-admin启用,nginx启用主机;之前是通过手动操作,很不方便,本次优化为…...

【巨人的肩膀】JAVA面试总结(七)
💪MyBatis 1、谈谈你对MyBatis的理解 Mybatis是一个半ORM(对象关系映射)框架,它内部封装了JDBC,加载驱动、创建连接、创建statement等繁杂的过程,开发者开发时只需要关注如何编写SQL语句,可以…...

Python满屏表白代码
目录 前言 爱心界面 无限弹窗 前言 人生苦短,我用Python!又是新的一周啦,本期博主给大家带来了一个全新的作品:满屏表白代码,无限弹窗版!快快收藏起来送给她吧~ 爱心界面 def Heart(): roottk.Tk…...
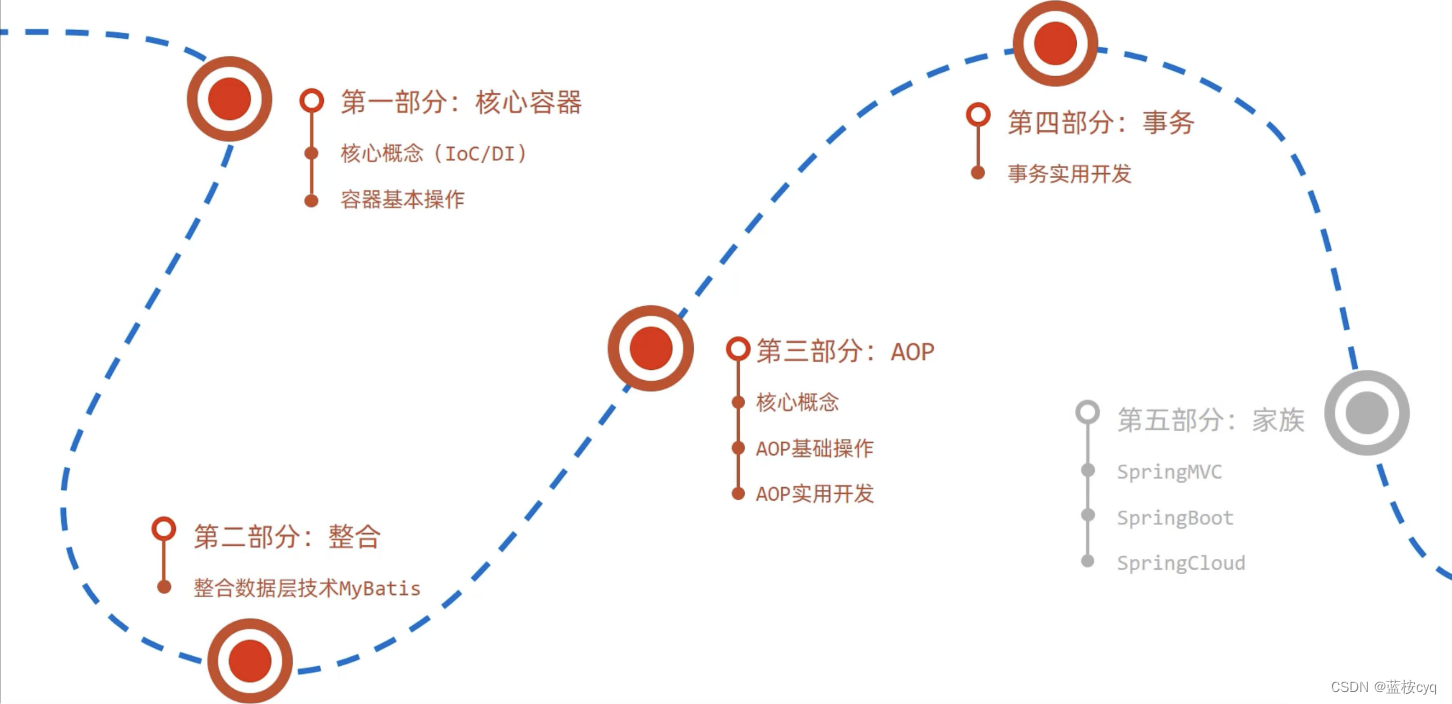
Spring学习流程介绍
Spring学习流程介绍 Spring技术是JavaEE开发必备技能,企业开发技术选型命中率>90%; Spring有下面两大优势: 简化开发: 降低企业级开发的复杂性 框架整合: 高效整合其他技术,提高企业级应用开发与运行效率 Spring官网: https://spring.io/ Spring发展…...
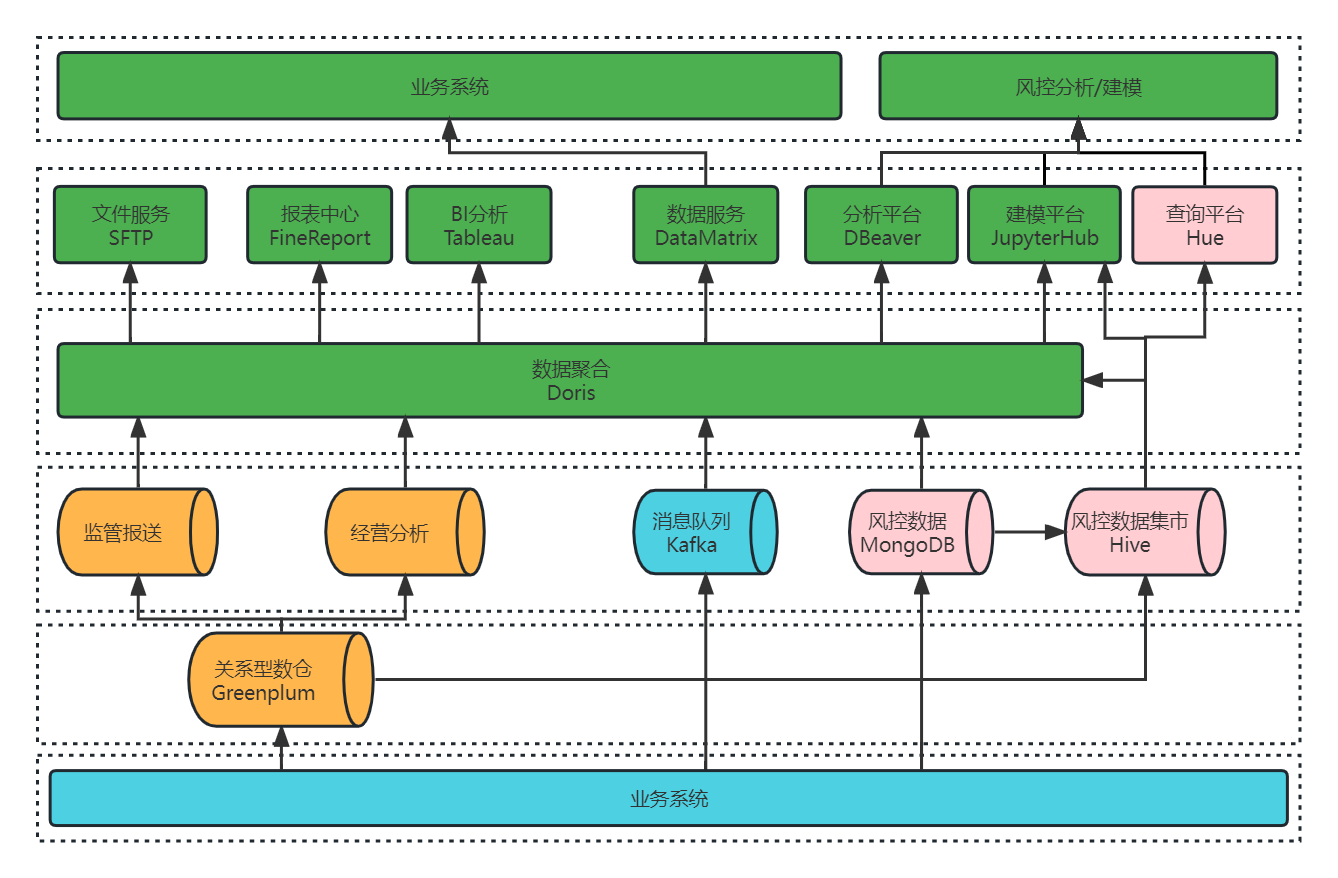
杭银消金基于 Apache Doris 的统一数据查询网关改造
导读: 随着业务量快速增长,数据规模的不断扩大,杭银消金早期的大数据平台在应对实时性更强、复杂度更高的的业务需求时存在瓶颈。为了更好的应对未来的数据规模增长,杭银消金于 2022 年 10 月正式引入 Apache Doris 1.2 对现有的风…...
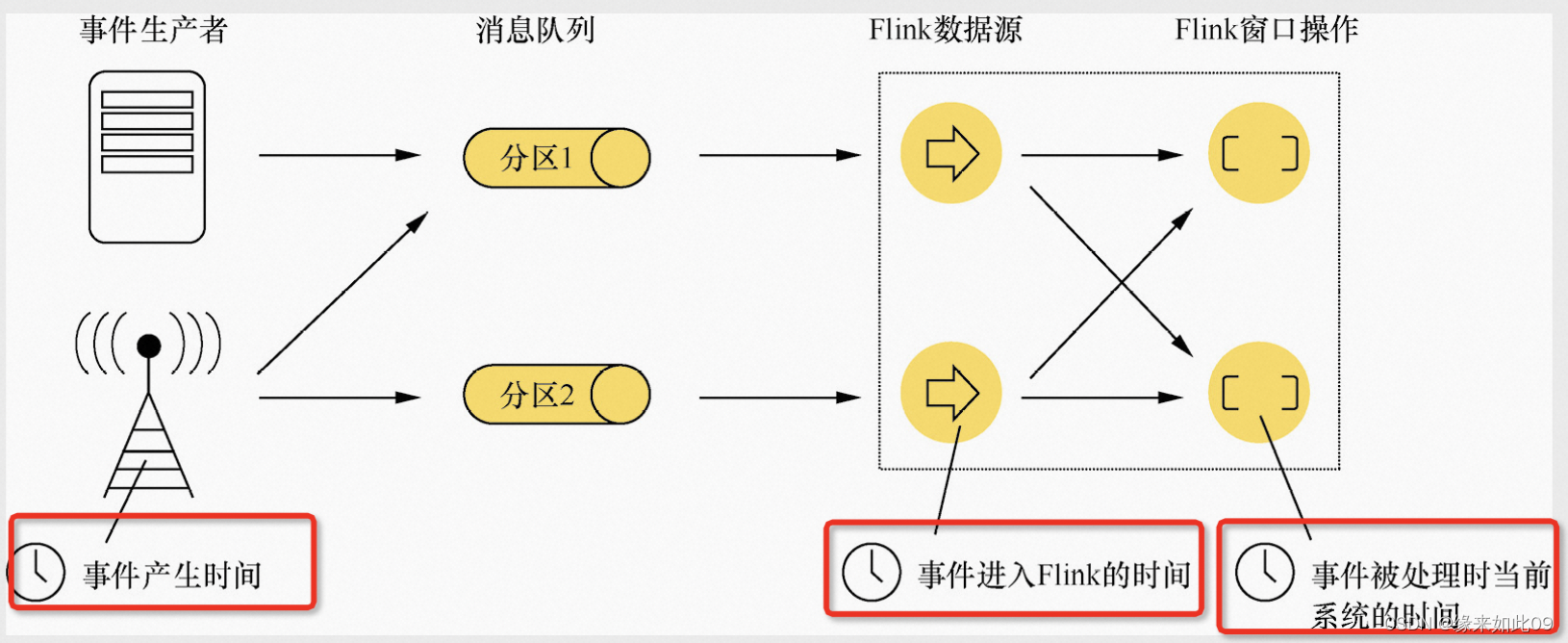
Flink学习笔记(六)Time详解
一、Flink中Time的三种类型: Stream数据中的Time(时间)分为以下3种: 1.Event Time(事件产生的时间): 事件的时间戳,通常是生成事件的时间。Event time 是事件本身的时间,…...

「Vue面试题」在项目中你是如何解决跨域的?
文章目录一、跨域是什么二、如何解决CORSProxy一、跨域是什么 跨域本质是浏览器基于同源策略的一种安全手段 同源策略(Sameoriginpolicy),是一种约定,它是浏览器最核心也最基本的安全功能 所谓同源(即指在同一个域&…...
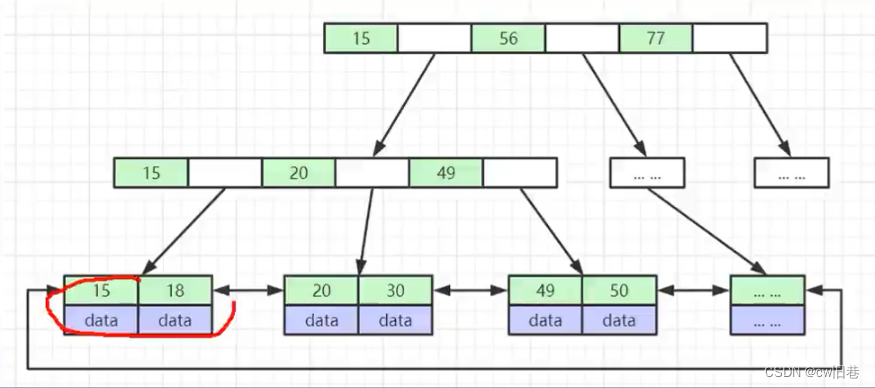
java八股文--数据库
数据库1.索引的基本原理2.聚簇和非聚簇索引的区别3.mysql索引的数据结构以及各自的优劣4.索引的设计原则5.事务的基本特性和隔离级别6.mysql主从同步原理7.简述MyISAM和InnoDB的区别8.简述mysql中索引类型及对数据库性能的影响9.Explain语句结果中各个字段分别表示什么10.索引覆…...

vue中名词解释
No名称略写作用应用场景其他1 单页面应用 (Single-page application) SPA 1,控制整个页面 2,抓取更新数据 3,无需加载,进行页面切换 丰富的交互,复杂的业务逻辑的web前端一般要求后端提供api数据…...

基于Java+SSM+Vue的旅游资源网站设计与实现【源码(完整源码请私聊)+论文+演示视频+包运行成功】
博主介绍:专注于Java技术领域和毕业项目实战 🍅文末获取源码联系🍅 👇🏻 精彩专栏推荐订阅👇🏻 不然下次找不到哟 Java项目精品实战案例(200套) 目录 一、效果演示 二、…...
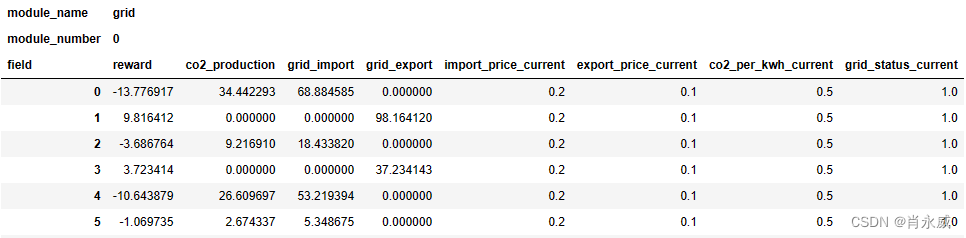
用于人工智能研究的开源Python微电网模拟器pymgrid(入门篇)
pymgrid是一个开源Python库,用于模拟微型电网的三级控制,允许用户创建或自行选择的微电网。并可以使用自定义的算法或pymgrid中包含的控制算法之一来控制这些微电网(基于规则的控制和模型预测控制)。 pymgrid还提供了与OpenAI Gy…...
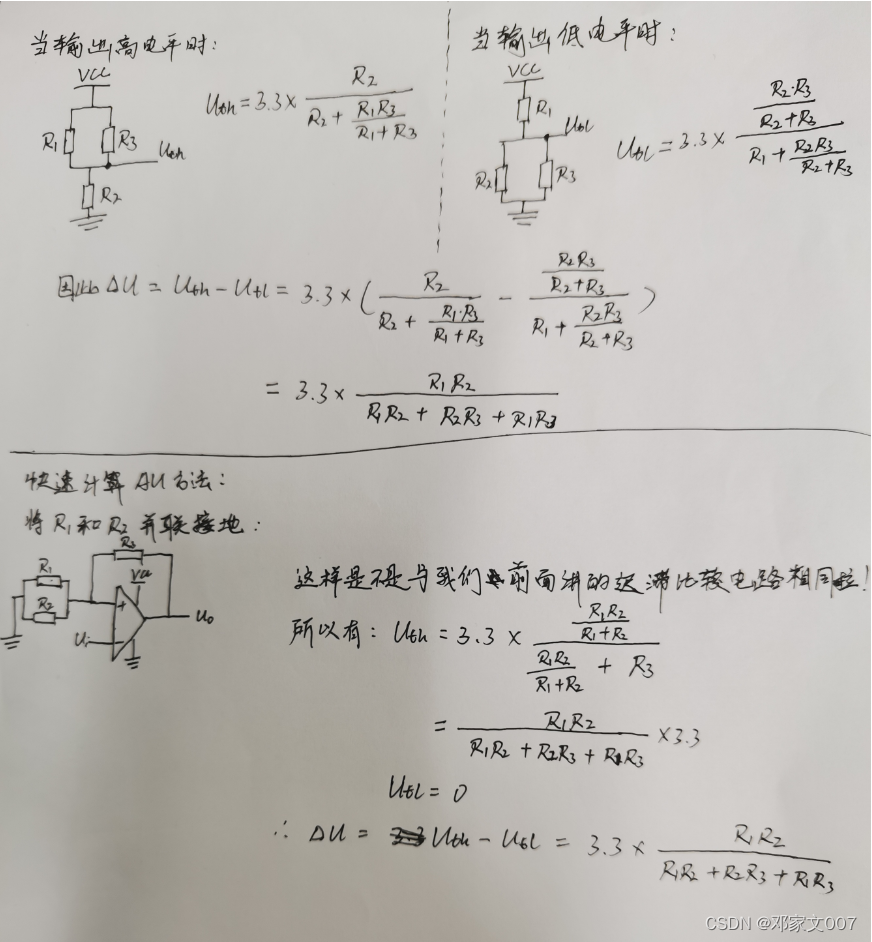
运算放大器:电压比较器、电压跟随器、同相比例放大器
目录一、单限电压比较器二、滞回电压比较器三、窗口电压比较器四、正点原子直流电机驱动器电路分析实战1、电压采集电路2、电流采集电路3、过流检测电路Ⅰ、采用分压后的输入电压:Ⅱ、采用理想电压源的输入电压:Ⅲ、同相输入电压采用的是非理想电压源&am…...

Vector - CAPL - 实时时间on *(续2)
继续继续。。。四、键盘事件这个键盘事件是我个人起的名字,为了方便与其他事件进行区分,为什么要把这一个单独拉出来说呢,因为它的用处实在是太广泛了,基本只要是使用CANoe做一些基本的自动化测试小工具,都会用到它&am…...

数据质量管理的四个阶段
然而,我们需要按照什么流程来对数据质量进行有效的管控,从而提升数据质量,释放数据价值?一般来讲,数据质量控制流程分为4个阶段:启动、执行、检查、处理。在管控过程中这4个阶段需不断循环,螺旋…...
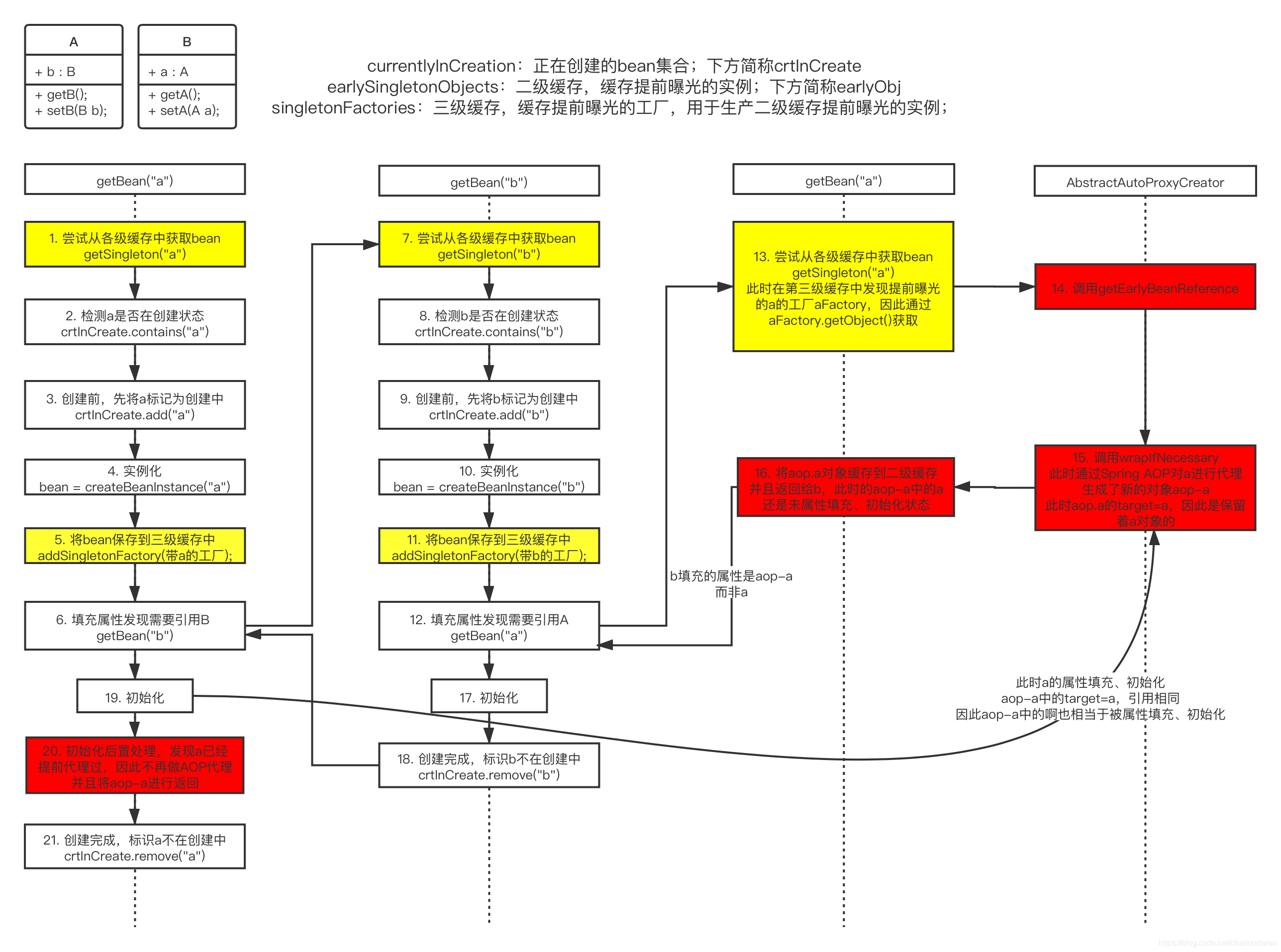
Spring源码面试最难问题——循环依赖
前言 问:Spring 如何解决循环依赖? 答:Spring 通过提前曝光机制,利用三级缓存解决循环依赖(这原理还是挺简单的,参考:三级缓存、图解循环依赖原理) 再问:Spring 通过提前…...
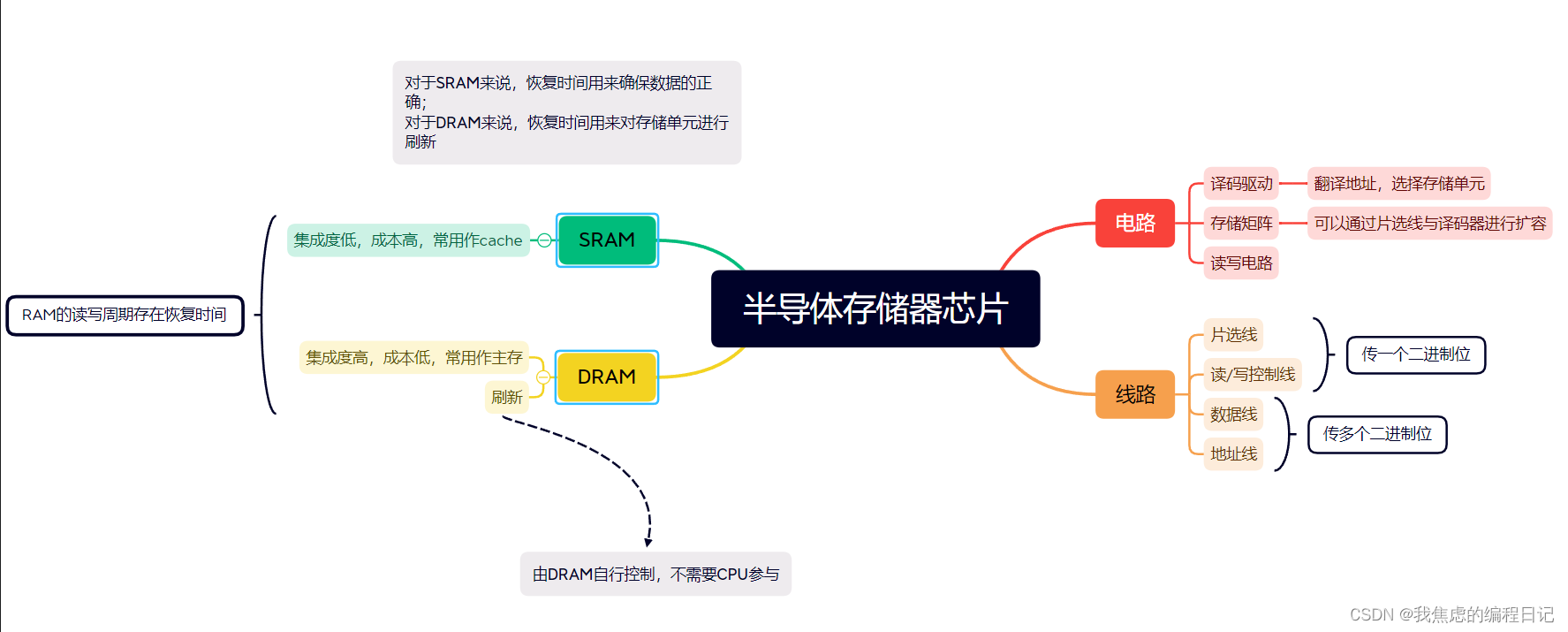
【计组】RAM的深入理解
一、存储机理 RAM的实现逻辑有种,分别是触发器和电容。 SRAM(Static)DRAM(Dynamic)存储方式触发器电容破坏性读出否(触发器具有稳态,能够锁住0或1两种状态)是(电容需要…...

JavaScript 之数据交互
在前后端交互中,前端通常需要对接口返回的数据进行格式转换、遍历、循环等;通常会用到以下函数和方法: forEach()、map()遍历数组(map返回新的数组);forEach()只能使用try catah终止循环;for in…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
