Mybatis_基础
文章目录
- 第一章 Mybatis简介
- 1.1 Mybatis特性
- 1.2 和其它持久化层技术对比
- 第二章 Mybatis的增删改查
- 第三章 Mybatis的增删改查
第一章 Mybatis简介
1.1 Mybatis特性
- MyBatis 是支持定制化 SQL、存储过程以及高级映射的优秀的持久层框架。
- MyBatis 避免了几乎所有的 JDBC 代码和手动设置参数以及获取结果集。
- MyBatis可以使用简单的XML或注解用于配置和原始映射,将接口和Java的POJO(Plain Old Java Objects,普通的Java对象)映射成数据库中的记录 。
- MyBatis 是一个 半自动的ORM(Object Relation Mapping)框架。
1.2 和其它持久化层技术对比
JDBC
- SQL 夹杂在Java代码中耦合度高,导致硬编码内伤。
- 维护不易且实际开发需求中 SQL 有变化,频繁修改的情况多见。
- 代码冗长,开发效率低。
Hibernate 和 JPA
- 操作简便,开发效率高。
- 程序中的长难复杂 SQL 需要绕过框架。
- 内部自动生产的 SQL,不容易做特殊优化。
- 基于全映射的全自动框架,大量字段的 POJO 进行部分映射时比较困难。
- 反射操作太多,导致数据库性能下降。
第二章 Mybatis的增删改查
查询的标签select必须设置属性resultType或resultMap,用于设置实体类和数据库表的映射关系:
- resultType:自动映射,用于属性名和表中字段名一致的情况。
- resultMap:自定义映射,用于一对多或多对一或字段名和属性名不一致的情况
第三章 Mybatis的增删改查
参考资料:
1.SSM框架全套课程_尚硅谷
相关文章:

Mybatis_基础
文章目录 第一章 Mybatis简介1.1 Mybatis特性1.2 和其它持久化层技术对比 第二章 Mybatis的增删改查第三章 Mybatis的增删改查 第一章 Mybatis简介 1.1 Mybatis特性 MyBatis 是支持定制化 SQL、存储过程以及高级映射的优秀的持久层框架。MyBatis 避免了几乎所有的 JDBC 代码和…...

8Manage采购申请管理:轻松实现手动采购流程自动化
您是否感受到通过手动采购申请流程管理成本的压力? 信息的不充分常常导致现金流的不透明,这已成为财务高管们的常见痛点。本文将展示采购申请管理软件如何帮助您减轻负担,使您能够简化流程。 没有采购申请软件会面临哪些挑战? …...

PADS Router 入门基础教程(一)
有将近三周没有更新过博客了,最近在整理PADS Router 入门基础教程,希望喜欢本系列教程的小伙伴可以点点关注和订阅!下面我们开始进入PADS Router课程的介绍。 一、PADS Router 快捷键 二、课程介绍 本教程主要介绍:PADS Rou…...

一台手机一个ip地址吗?手机ip地址泄露了怎么办
在数字化时代,手机作为我们日常生活中不可或缺的一部分,其网络安全性也日益受到关注。其中一个常见的疑问便是:“一台手机是否对应一个固定的IP地址?”实际上,情况并非如此简单。本文首先解答这一问题&a…...

【扇贝编程】使用Selenium模拟浏览器获取动态内容笔记
文章目录 selenium安装 selenium下载浏览器驱动 获取数据处理数据查找一个元素查找所有符合条件的元素 控制浏览器 selenium selenium是爬虫的好帮手, 可以控制你的浏览器,模仿人浏览网页,从而获取数据,自动操作等。 我们只要让…...

TCP Analysis Flags 之 TCP Port numbers reused
前言 默认情况下,Wireshark 的 TCP 解析器会跟踪每个 TCP 会话的状态,并在检测到问题或潜在问题时提供额外的信息。在第一次打开捕获文件时,会对每个 TCP 数据包进行一次分析,数据包按照它们在数据包列表中出现的顺序进行处理。可…...

【Python机器学习】核心数、进程、线程、超线程、L1、L2、L3级缓存
如何知道自己电脑的CPU是几核的,打开任务管理器(同时按下:Esc键、SHIFT键、CTRL键) 然后,点击任务管理器左上角的性能选项,观察右下角中的内核:后面的数字,就是你CPU的核心数,下图中我的是16个核心的。 需要注意的是,下面的逻辑处理器:32 表示支持 32 线程(即超线…...

JavaScript使用地理位置 API
前言 在JavaScript中,Geolocation API 是一种用于访问用户地理位置的接口。这个API允许网页应用程序获取用户的位置并提供基于位置的服务。 if (navigator.geolocation)navigator.geolocation.getCurrentPosition(function () {},function () {});这个函数中需要传…...

dockerfile部署fastapi项目
dockerfile部署fastapi项目 1、Dockerfile # 使用Python官方镜像作为基础镜像 FROM python:3.8-slim# 更新apt-get源并安装依赖 # RUN apt-get update -y && apt-get install -y git# 设置环境变量 ENV PYTHONDONTWRITEBYTECODE 1 ENV PYTHONUNBUFFERED 1# 创建工作目…...
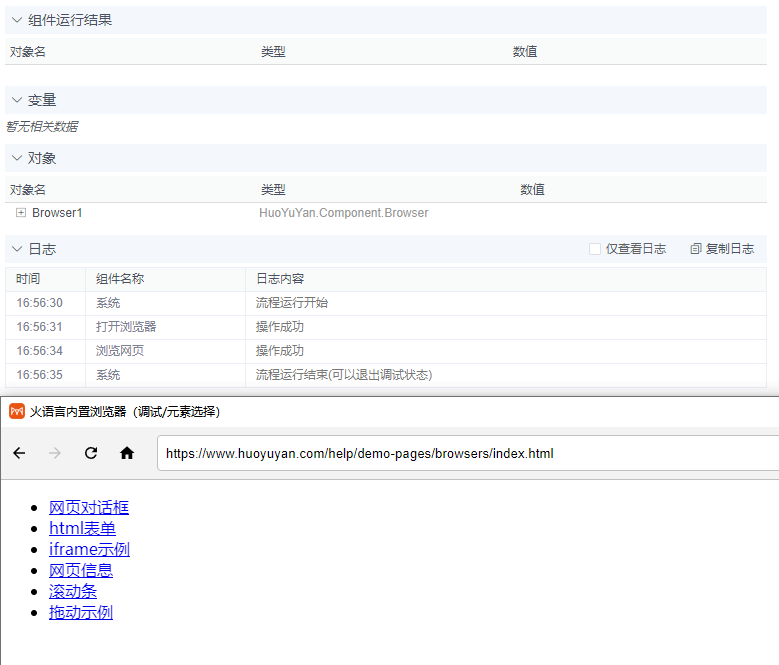
火语言RPA流程组件介绍--浏览网页
🚩【组件功能】:浏览器打开指定网址或本地html文件 配置预览 配置说明 网址URL 支持T或# 默认FLOW输入项 输入需要打开的网址URL 超时时间 支持T或# 打开网页超时时间 执行后后等待时间(ms) 支持T或# 当前组件执行完成后继续等待的时间 UserAgen…...

【Linux系统学习】2.Linux基础命令
Linux基础命令 Linux的目录结构 Linux命令入门 目录切换相关命令(cd/pwd) 相对路径、绝对路径和特殊路径符 创建目录命令(mkdir) 文件操作命令part1(touch、cat、more) 文件操作命令part2(cp、mv、rm) 查找命令(which、find) grep、wc和管道符…...

ABAP正则表达式 特殊字符处理
REPLACE ALL OCCURRENCES OF REGEX [[:space:]] IN <fs_purhdinfo>-cell_value WITH ."可去掉空格或回车键 REPLACE ALL OCCURRENCES OF : IN <fs_purhdinfo>-cell_value WITH ."可去掉空格或回车键 REPLACE ALL OCCURRENCES OF R…...

【2024高教社杯全国大学生数学建模竞赛】ABCDEF题 问题分析、模型建立、参考文献及实现代码
【2024高教社杯全国大学生数学建模竞赛】ABCDEF题 问题分析、模型建立、参考文献及实现代码 1 比赛时间 北京时间:2024年9月5日 18:00-2024年9月8日20:00 2 思路内容 2.1 往届比赛资料 【2022高教社杯数学建模】C题:古代玻璃制品的成分分析与鉴别方案…...

# VMware 共享文件
VMware tools快速安装 VMware 提供了 open-vm-tools,这是 VMware 官方推荐的开源工具包,通常不需要手动安装 VMware Tools,因为大多数 Linux 发行版(包括 Ubuntu、CentOS 等)都包含了 open-vm-tools,并且已…...

[UVM]3.核心基类 uvm_object 域的自动化 copy() compare() print() pack unpack
1.核心基类:uvm_object (1)虚类只能声明,不能例化。 (2)uvm_object提供的方法 2.域的自动化(field automation) (1)简述 (2)示例 格…...

Java网络编程入门
在现代软件开发中,网络编程是一项不可或缺的技能。Java提供了强大的网络编程支持,使得开发者能够轻松地创建网络应用程序。今天将介绍Java中的网络编程基础,重点讲解Socket和ServerSocket类的使用。 什么是Socket? Socket是网络通…...
)
前端基础面试题·第三篇——JavaScript(其一)
1.JavaScript数据类型与运算符 数据类型 原始数据类型: 1.Number 2.String 3.Boolean 4.undefined 5.null 6.Symbol 7.bigint 复杂数据类型: 1.Function 2.非函数: Array: 数组 Object: 对象 Date: 日期 RegExp: 正则 Map: 映射 Set: 集合 …...

【机器学习】生成对抗网络(Generative Adversarial Networks, GANs)详解
1.引言 生成对抗网络(Generative Adversarial Networks, GANs)是近年来人工智能领域最具创新性和颠覆性的模型之一。自2014年由Ian Goodfellow及其团队提出以来,GAN的出现彻底改变了生成模型的研究范式。传统的生成模型,如变分自编码器(VAE)、隐马尔可夫模型(HMM)等,…...

QT作业1
1> 手写unique_ptr指针指针 代码: #include <iostream>using namespace std;// 自定义的unique_ptr类模板 template <typename T> class unique_ptr { public:// 构造函数,接收一个指针explicit unique_ptr(T* ptr nullptr) noexcept …...

Mybatis-设计模式总结
1、Builder模式 Builder模式的定义是“将一个复杂对象的构建与它的表示分离,使得同样的构建过程可以创建不同的表示。”,它属于创建类模式,一般来说,如果一个对象的构建比较复杂,超出了构造函数所能包含的范围&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
