Codeforces Round 970 (Div. 3)(ABCDEF)
Codeforces Round 970 (Div. 3)
A:Sakurako's Exams
签到
题意:给定1,2的数量,判断是否能用加减符号使得这些1,2计算出0
void solve()
{cin>>n>>m;if(n%2)cout<<"NO\n";else{if(m%2==0||n)cout<<"YES\n";else cout<<"NO\n";}return ;
}B:Square or Not
签到
题意:给定01序列,问从上到下,从左到右排列是否可以得到一个周围为1,内部为0的正方形
void solve()
{string s;cin>>n;cin>>s;int t=sqrt(n);if(t*t!=n){cout<<"No\n";return;}else {int idx=0;for(int i=0;i<t;i++){for(int j=0;j<t;j++){int now=i*t+j;if(i==0||j==0||i==t-1||j==t-1){if(s[now]=='0'){cout<<"No\n";return;}}else if(s[now]=='1'){cout<<"No\n";return;}}}}cout<<"Yes\n";return ;
}C:Longest Good Arrays
题意:给定左右边界了l,r,问在范围内凑出最长的满足a[i]-a[i-1]<a[i+1]-a[i](i>=2)的最长数组的长度
思路:最优一定是前后两项差从左到右分别为1,2,3,4...,所以二分数组最后一个元素,满足小于r-l的第一个元素位置,再+1就是答案
int n,m;
int cha;
bool check(int x)
{return (x+1)*x/2>cha;
}
void solve()
{cin>>n>>m;cha=m-n;int l=0,r=1e8;while(l+1<r){int mid=l+r>>1;check(mid)?r=mid:l=mid;}cout<<l+1<<'\n';return ;
}D:Sakurako's Hobby
题意:输入一个数组大小n,然后输入n个数q[i](1<=i<=n)代表i可以到达q[i](保证q数组一定是一个排列),然后输入一个01串,当第i个位置为‘1’代表为白块,为'0'代表为黑块,f[i]为能够到达i这个点的所有黑块的数量,输出所有f[i](1<=i<=n)
例如:
输入
2
2 1
00
输出
2 2
(因为1位置的点都能由1,2到达)
思路:并查集,把所有有联系的点都缩到一个根上(由于是一个排列,所以所有可以直接可以到达或者间接到达的点都可以形成一个环,也就是相互到达),最后问f[i]只需要把一个环中的所有店都累加到find(i),也就是根节点上
代码:
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <cmath>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define pp pop_back()
#define int long long
#define laile cout<<"laile"<<endl
#define lowbit(x) ((x)&(-x))
#define double long double
#define sf(x) scanf("%lld",&x)
#define sff(x,y) scanf("%lld %lld",&x,&y)
#define sd(x) scanf("%Lf",&x)
#define sdd(x,y) scanf("%Lf %Lf",&x,&y)
#define _for(i,n) for(int i=0;i<(n);++i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
#define _pre(i,a,b) for(int i=(a);i>=(b);--i)
#define all(x) (x).begin(), (x).end()
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
typedef unsigned long long ULL;
typedef pair<int,int>PII;
const int N=1e6+10,INF=4e18;
int n,m;
int f[N],q[N],cnt[N];
bool st[N];
int find(int x)
{if(x!=f[x])return f[x]=find(f[x]);return f[x];
}
void root(int a,int b)
{int x=find(a),y=find(b);if(x!=y)f[x]=y;
}
void solve()
{cin>>n;_rep(i,1,n)cin>>q[i],f[i]=i,st[i]=false,cnt[i]=0;string s;cin>>s;s=" "+s;_rep(i,1,n){int now=i;while(!st[now]){st[now]=true;root(now,q[now]);now=q[now];}} _rep(i,1,n)if(s[i]=='0')cnt[find(i)]++;_rep(i,1,n)cout<<cnt[find(i)]<<" ";cout<<'\n';return ;
}
signed main()
{IOS;int T=1;cin>>T;while(T--)solve();return 0;
}E:Alternating String
题意:给定一个字符串,现在有两个操作
1:选一个字母删除(但是这个最多只能操作一次)
2:将一个位置的字母改成另一个字母
问你把这个字符串变成一个:奇数位置字母都相同,偶数位置字母都相同 的字符串的最小操作次数
思路
只要发现一个特点就可以想到这个思路,那就是当你选择把当前这个点i的字母删除之后,后面所有的字母所在的奇偶位置就发生了互换
1.首先考虑不删除字母的情况
维护一个hou[26][2]的数组,其中第一维代表哪个字母(0~25),第二维 0/1 代表 奇数位/偶数位
那么我首先遍历奇数位置的所有字母,求和sum就是奇数位置字母的数量,求最大值ma就是奇数位置 字母的众数那么sum-ma就是奇数位置最少需要改变的字母的数量
偶数位置同理,那么就能求导不删除字母情况下最小操作次数
2,考虑删除字母的情况
假如我现在删除的是i号点,那么1~i-1号点的奇偶性质未发生改变,那么我就从小到大遍历即可,i+1~n号点的奇偶性质全部发生了改变,那么显然如果我能预处理出i+1~n的所有状态,也就是前面说到的hou[26][2],那么奇数位本来是hou[0~25][0]现在只需要考虑hou[0~25][1],偶数位置同理,那么就可以发现这个hou[0~25][2]显然可以提前预处理出来,然后遍历到第i个点的时候把1~i的状态删去就行,这些都可以线性处理,时间复杂度O(26*n)
代码:
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <cmath>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define pp pop_back()
#define int long long
#define laile cout<<"laile"<<endl
#define lowbit(x) ((x)&(-x))
#define double long double
#define sf(x) scanf("%lld",&x)
#define sff(x,y) scanf("%lld %lld",&x,&y)
#define sd(x) scanf("%Lf",&x)
#define sdd(x,y) scanf("%Lf %Lf",&x,&y)
#define _for(i,n) for(int i=0;i<(n);++i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
#define _pre(i,a,b) for(int i=(a);i>=(b);--i)
#define all(x) (x).begin(), (x).end()
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
typedef unsigned long long ULL;
typedef pair<int,int>PII;
const int N=1e6+10,INF=4e18;
int n,m;
int now[26][2],hou[26][2];//now储存1~i-1的状态,hou储存i+1~n的状态
void solve()
{cin>>n;string s;cin>>s;memset(now,0,sizeof(now));memset(hou,0,sizeof(hou));s=" "+s;_rep(i,1,n)hou[s[i]-'a'][i%2]++;int res=0,sum,ma;_rep(j,0,1){sum=0; ma=0;_rep(i,0,25){sum+=hou[i][j];ma=max(hou[i][j],ma);}res+=sum-ma;}if(n%2){res=INF;_rep(i,1,n){int nowres=0;hou[s[i]-'a'][i%2]--;_rep(j,0,1){sum=0;ma=0;_rep(k,0,25){sum+=hou[k][j];sum+=now[k][j^1];ma=max(ma,hou[k][j]+now[k][j^1]);}nowres+=sum-ma;}now[s[i]-'a'][i%2]++;res=min(res,nowres+1);}}cout<<res<<"\n";return ;
}
signed main()
{IOS;int T=1;cin>>T;while(T--)solve();return 0;
}F:Sakurako's Boxt
题意:给定一个数组,为元素之间两两相乘(a[1]*a[2]和a[2]*a[1]重复不算)的平均数是什么
思路:
假设四个元素
那么答案就是
等价于
用一个后缀和维护形如的东西这道题就轻松解决了,只需要注意一下取模和乘法逆元的问题就行了
#include <map>
#include <set>
#include <queue>
#include <deque>
#include <cmath>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
using namespace std;
#define fi first
#define se second
#define pb push_back
#define pp pop_back()
#define int long long
#define laile cout<<"laile"<<endl
#define lowbit(x) ((x)&(-x))
#define double long double
#define sf(x) scanf("%lld",&x)
#define sff(x,y) scanf("%lld %lld",&x,&y)
#define sd(x) scanf("%Lf",&x)
#define sdd(x,y) scanf("%Lf %Lf",&x,&y)
#define _for(i,n) for(int i=0;i<(n);++i)
#define _rep(i,a,b) for(int i=(a);i<=(b);++i)
#define _pre(i,a,b) for(int i=(a);i>=(b);--i)
#define all(x) (x).begin(), (x).end()
#define IOS ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
typedef unsigned long long ULL;
typedef pair<int,int>PII;
const int N=1e6+10,INF=4e18,P=1e9+7;
int n,m;
int hou[N],q[N];
int qmi(int a,int b)
{int res=1;while(b){if(b&1)res=res*a%P;a=a*a%P;b>>=1;}return res;
}
void solve()
{cin>>n;_rep(i,1,n)cin>>q[i];hou[n+1]=0;_pre(i,n,1)hou[i]=hou[i+1]+q[i];int res=0;_rep(i,1,n){res+=(q[i]*(hou[i+1]%P)%P);res%=P;}
// cout<<"res="<<res<<" "<<n<<endl;cout<<(res*qmi((n*(n-1)/2)%P,P-2)%P)<<'\n';return ;
}
signed main()
{IOS;int T=1;cin>>T;while(T--)solve();return 0;
}相关文章:
Codeforces Round 970 (Div. 3)(ABCDEF)
Codeforces Round 970 (Div. 3) A:Sakurakos Exams 签到 题意:给定1,2的数量,判断是否能用加减符号使得这些1,2计算出0 void solve() {cin>>n>>m;if(n%2)cout<<"NO\n";else{if(m%20||n)cout<<"YES\n";else cout<<"…...

springboot基于ssm+Jsp的人才招聘网站系统的设计与实现 jw2cs
目录 前言详细视频演示后端技术栈具体实现截图开发核心技术:开发工具核心代码部分展示系统设计操作可行性可行性论证试验方案源码获取 前言 👇🏻 博主介绍:👇🏻 全网粉丝50W,博客专家、CSDN特邀作者、CSDN…...

高质量共建“一带一路”!苏州金龙助力非洲交通驶向共同繁荣之旅
9月6日,中非合作论坛在北京落下帷幕。此次论坛,“高质量共建‘一带一路’”成为重要议题。截止至目前,苏州金龙海格客车已向阿尔及利亚、埃塞俄比亚、南非等所有参与共建“一带一路”的非洲国家累计出口客车14000台。从产品销售,到…...

嵌入式初学-C语言-数据结构--四
栈 1. 基本概念 栈是一种逻辑结构,是特殊的线性表。特殊在: 只能在固定的一端操作 只要满足上述条件,那么这种特殊的线性表就会呈现一种“后进先出”的逻辑,这种逻辑就被称为栈。栈 在生活中到处可见,比如堆叠的盘子…...

【HarmonyOS 4】应用性能优化
1. ArkTs 高性能编程 1.1 ArkTs 高性能编程规则 1.1.1 限制一些 TypeScript 的特性,比如需要不支持属性的动态变更、变量或参数需要明确的类型声明和返回值声明等。1.1.2 禁用 ts-ignore、ts-expect-error 等屏蔽编译校验的命令。1.1.3 开启 TypeScript 的严格模式…...

MySQL——表操作
目录 一、创建表 二、查看表 2.1 查看表中某成员的数据 2.2 查看整个表中的表成员 2.3 查看创建表时的句柄 三、修改表 alter 3.1 重命名 rename 3.2 新增一列 add 3.3 更改列属性 modify 3.4 更改列名称 change 3.5 删除某列 上一篇博客介绍了库的操作,…...
)
阅读笔记--Guiding Attention in End-to-End Driving Models(二)
端到端驾驶的注意力学习(Attention Learning for End-to-End Driving)关键内容学习 3.1 问题设置(Problem Setup) 模仿学习(Imitation Learning, IL):介绍了模仿学习的概念,即通过…...

Linux: network: TCP: errno: EWOULDBLOCK
https://mzhan017.blog.csdn.net/article/details/108010013 这个errno的意思: 如果是send接口函数返回的错误,代表tcp socket的sending buffer满了,让应用程序等上一段时间重试send。 所以,这个产生的原因就不固定了: 可能是当前系统太忙,导致系统发包慢,buffer累积; 可…...

闲话“设计模式”
Q1、请详细介绍 软件架构设计模式(智能化),应用程序设计模式(自动化),编程语言设计模式(人性化)(后面括号中 是我 希望 其 具有的特点) 的概念,有…...
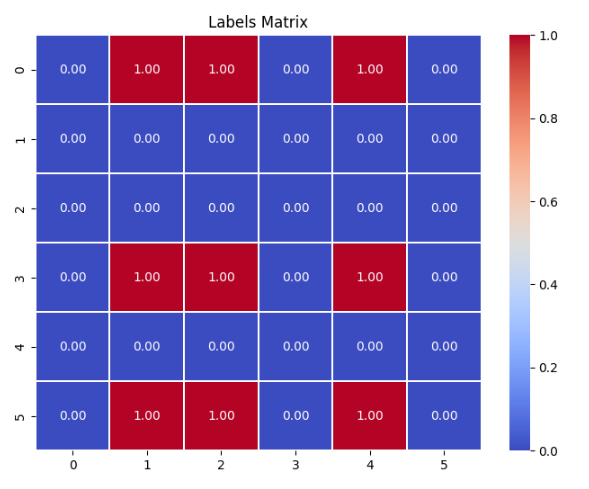
Sentence-BERT实现文本匹配【CoSENT损失】
引言 还是基于Sentence-BERT架构,或者说Bi-Encoder架构,但是本文使用的是苏神提出的CoSENT损失函数1。 点击来都是缘分,之前过时的方法可以不细看,别的文章可以不收藏,现在是最流行的方法,这篇文章建议收藏…...

业余考什么证书比较实用?
在业余时间里,获得一些有用的证书不仅能提升你的专业素养,还能增强你在职场上的竞争力。 特别是职业技能证书和行业认证证书,这两者受到了广大职场人士的高度关注。 一、业余时间考取的实用证书 行业认证证书主要针对特定行业或职业&#…...

16款facebook辅助工具,总有一款适合你!
Hey小伙伴们~👋 是不是想利用FB大展拳脚,却苦于不知道如何开始?别急,今天就给你们安利16个超实用的FB营销工具,涵盖了内容创建和发布的应用程序,以及数据追踪分析、商品销售等多个方面让你轻松get海外获客新…...

给网站发外链的好处,你了解多少?
在当今这个信息爆炸的互联网时代,网站优化和推广成为了每一个网站主不可忽视的重要环节。其中,给网站发外链,即在其他网站上设置指向自己网站的链接,是一种高效且被广泛采用的策略。那么,给网站发外链究竟能带来哪些好…...

安卓链接正常显示,ios#符被转义%23导致链接访问404
原因分析: url中含有特殊字符 中文未编码 都有可能导致URL转换失败,所以需要对url编码处理 如下: guard let allowUrl webUrl.addingPercentEncoding(withAllowedCharacters: .urlQueryAllowed) else {return} 后面发现当url中有#号时&a…...

excel分列
Excel中有这么几列,希望将每一列内容再分出3列: 可以通过以下步骤在 Excel 表格中将 B 到 F 列的内容拆分为每列的 3 列,分别为 pred_label、pred_score 和 pred_class: 确定数据结构:假设 B 列到 F 列中的内容都是按类…...

STM32 HAL DMA 中断碰到的问题
流程 串口收数据—>dma搬运到变量—>空闲中断----->接收完成 配置 dma中断全部去掉 串口中断开启 freertos中断全部去掉 时钟配置 代码 开启中断 // DMA 空闲检查 void receives_uaru_7(void) {RXU7 0;//清除中断标志HAL_UARTEx_ReceiveToIdle_DMA(&hua…...

让树莓派智能语音助手实现定时提醒功能
最初的时候是想直接在rasa 的chatbot上实现,因为rasa本身是带有remindschedule模块的。不过经过一番折腾后,忽然发现,chatbot上实现的定时,语音助手不一定会有响应。因为,我目前语音助手的代码设置了长时间无应答会结束…...
AIoTedge边缘计算+边缘物联网平台
在数字化转型的浪潮中,AIoTedge边缘计算平台以其边云协同的架构和强大的分布式AIoT处理能力,正成为推动智能技术发展的关键力量。AIoTedge通过在数据源附近处理信息,实现低延迟、快速响应,增强了应用的实时性。同时,它…...

Java使用拷贝asset文件,解密,并用DexclassLoader加载执行
//asset中加密的apk文件重命名为index.html,拷贝到私有目录 //解密 //加载,执行apk中的方法 public static void handleByJava(Context context){File copyedFile new File(context.getFilesDir().getAbsolutePath() "/" "main.html");FileUtil.copyAss…...

【AcWing】861. 二分图的最大匹配(匈牙利算法)
匈牙利算法,他可以在比较快的时间复杂度之内告诉我们左边和右边成功匹配的最大数是多少 匹配指的是边的数量,成功的匹配指的是两个未被使用的点之间存在一条边(就不存在两条边共用了一个点的)。 匈牙利算法可以返回成功匹配的最大匹配数是多少。 #incl…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
