哈希表 and 算法
哈希表:
哈希表(Hash table),也被称为散列表,是一种根据关键码值(Key value)而直接进行访问的数据结构。它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数被称为散列函数或哈希函数,而存放记录的数组则被称为散列表或哈希表。
哈希表的优点
- 查找速度快:哈希表通过哈希函数直接定位到数组中的位置,因此查找速度非常快,时间复杂度接近O(1)。
- 插入和删除操作方便:由于哈希表是基于数组实现的,因此插入和删除操作也相对简单。
- 空间利用率高:哈希表通过哈希函数将关键码值映射到有限的数组空间中,可以高效地利用存储空间。
哈希表的缺点
- 冲突问题:不同的关键码值可能通过哈希函数得到相同的哈希值,即产生冲突。解决冲突的方法有多种,如开放寻址法、链地址法等。
- 哈希函数的选择:哈希函数的选择对哈希表的性能有很大影响。一个好的哈希函数应该能够均匀地分布哈希值,减少冲突的发生。
- 动态扩容问题:当哈希表中的元素数量增加到一定程度时,可能需要进行动态扩容以维持性能。扩容操作会涉及到数据的重新哈希和存储,可能会带来一定的性能开销。
#include "hash.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>HSNode_t *hashtable[HASH_SIZE] = {NULL};int hash_function(char key) //哈希表函数
{if (key >='a'&&key<='z'){return key - 'a';}else if(key >= 'A'&&key <= 'Z'){return key - 'A';}else{return HASH_SIZE-1;}
}int intsert_hashtable(HSDataType data)//向哈希表添加元素
{int addr = hash_function(data.name[0]);HSNode_t *pnode =(HSNode_t*)malloc(sizeof(HSNode_t));if(pnode == NULL){perror("malloc fail");return 0;}pnode->data = data;pnode -> pnext = NULL;if(hashtable[addr] == NULL){hashtable[addr] = pnode;return 0;}pnode ->pnext = hashtable[addr]->pnext;hashtable[addr]->pnext = pnode;return 0;
}HSNode_t *find_hashtable(char *name)//查找
{int addr = hash_function(name[0]);HSNode_t *p = hashtable[addr];while(p != NULL){if(!strncmp(p->data.name,name,strlen(name))){break;}p = p->pnext;}return p;
}void print_hashtable()//打印哈希表
{int i = 0;for( i = 0 ; i<HASH_SIZE;++i){HSNode_t *p = hashtable[i];while( p!= NULL){printf("%s,%s\n",p->data.name,p->data.tel);p = p->pnext;}}return ;
}void destroy_hashtable()//销毁哈希表
{for (int i = 0;i < HASH_SIZE;++i){while(hashtable[i] != NULL){HSNode_t *p = hashtable[i];hashtable[i] = p->pnext;free (p);}}
}
算法:
排序:
选择排序法:
基本思想:
第1次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后 再从剩余的元素中选择最小(或最大)的元素,然后放到已排序的序列的末尾。以此类推, 直到全部待排序的数据元素排完。
时间复杂度:O(n^2)
稳定性:不稳定
代码:
int main(void)
{int a[] = {1,2,4,3,6,7,8,5,9,0};int len = sizeof(a) / sizeof(a[0]);int i,j;for(i = 0;i < len -1;++i){for(j = i + 1;j < len;++j){if(a[i] > a[j]){int t;t = a[i];a[i] = a[j];a[j] = t;}}}
}插入排序法:
基本思想:
是将一个记录插入到已经排好序的有序表中,从而得到一个新的、记录数增加1的有序表。在 整个排序过程中,我们反复地将一个记录插入到前面已排好序的序列中,直到全部记录插入 完成,排序也就结束了。
时间复杂度:O(n^2)
稳定性:不稳定
代码:
int main(void)
{int a[] = {1,4,5,6,2,8,3,7,9,0};int len = sizeof(a) / sizeof(a[0]);int i;for(i = 1; i< len;++i){int j;int t = a[i];j = i;while(j >0 && a[j - 1]>t){a[j] = a[j - 1];--j;}a[j] = t;}return 0;
}冒泡排序法:
基本思想:
通过重复地遍历要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过 来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
时间复杂度:O(n^2)
稳定性:稳定
代码
int main(void)
{int a[] = {1,4,5,6,2,8,3,7,9,0};int len = sizeof(a) / sizeof(a[0]);int i,j;for(j = len - 1;j > 0;--j){for(i = 0;i < j;++i){if(a[i] > a[i + 1]){int t;t = a[i];a[i] = a[i + 1];a[i + 1] = t;}}}return 0;
}快速排序法:
基本思想:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分 的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以 递归进行,以此达到整个数据变成有序序列。
时间复杂度:O(n log n)
稳定性:不稳定
代码:
#include <stdio.h>void print_array(int *a,int len)
{for(int i = 0;i < len ;++i){printf("%d,",a[i]);}printf("\n");
}void quick_sort(int *a,int begin ,int end)
{int i = begin;int j = end;int key = a[i];if(i > j){return ;}while(i < j){while(i<j && a[j] >= key){--j;}a[i] = a[j];while(i < j && a[i] <= key){++i;}a[j] = a[i];}a[i] = key;quick_sort(a,begin,i-1);quick_sort(a,i+1,end);
}int main(int argc, char *argv[])
{int a[] = {1,-1,3,2,4,-5,6,-7,8,9}; int len = sizeof(a)/sizeof(a[0]);quick_sort(a,0,len-1);print_array(a,len);return 0;
}相关文章:

哈希表 and 算法
哈希表: 哈希表(Hash table),也被称为散列表,是一种根据关键码值(Key value)而直接进行访问的数据结构。它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射…...
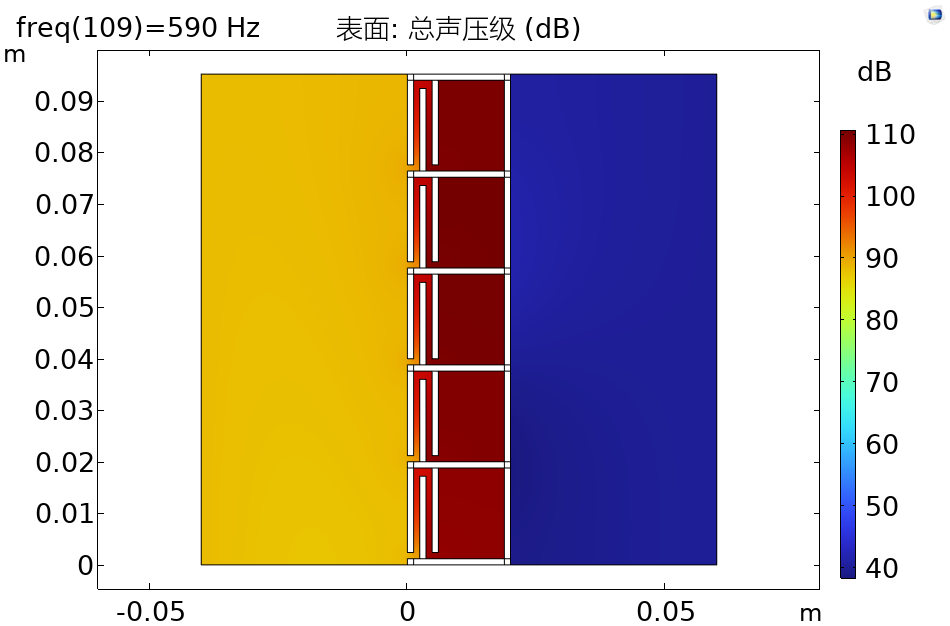
Comsol 共用声固耦合边界与热粘性声学边界的亥姆霍兹腔体超材料板精准隔声设计
声子晶体可分为局域共振型声子晶体和布拉格散射型声子晶体, 由于布拉格声子晶体需要的结构尺寸往往很大, 不便于实际应用; 而基于局域共振型机理的声子晶体能够实现“小体积控制大波长”, 因而有更加广泛的应用, 其中利用Helmholtz共鸣腔是局域共振型机理的典型应用, 近年来, H…...

Linux系统本地化部署Dify并安装Ollama运行llava大语言模型详细教程
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

极光出席深圳国际人工智能展并荣获“最具投资价值人工智能奖”
9月8-10日,由深圳市工业和信息化局、深圳市发展和改革委员会、深圳市科技创新局、深圳市政务服务和数据管理局、深圳市中小企业服务局共同指导,深圳市人工智能行业协会主办的第五届深圳国际人工智能展正式开幕。作为中国领先的客户互动和营销科技服务商&…...

人工智能领域的性能指的是什么
目录 1. 准确性(Accuracy) 2. 精确率与召回率(Precision & Recall) 3. F1分数 4. 运行时间与延迟(Latency) 5. 吞吐量(Throughput) 6. 可扩展性(Scalability&a…...

SQL进阶技巧:如何利用SQL解决趣味赛马问题?| 非等值关联匹配问题
目录 0 问题描述 1 数据准备 2 问题分析 方法一:先分后合思想 方法2:非等值关联匹配 3 小结 0 问题描述 有一张赛马记录表,如下所示: create table RacingResults ( trace_id char(3) not null,race_date date not null, race_nbr int not null,win_name char(30) n…...

Vue Echarts报错Initialize failed: invalid dom解决方法
此问题是图表初始化时 找不到dom,以下是解决方法 1、不要用created(用mounted),created这时候还只是创建了实例,但模板还没挂载完成; created: 在模板渲染成 html 前调用,通常初始…...

MySQL—死锁
什么是死锁? 好比是两个事务都在等待对方释放锁,之后进行下一步操作,但是最后双方都没有释放资源,所以导致一直处于等待的状态。 但是服务器不会让死锁的状态一直持续,会关闭其中一个影响较小的事务(右边的…...

CS5363|CS5263升级方案|DP转HDMI 4K60HZ芯片方案
CS5363是一种高度集成的单芯片,适用于多个细分市场和显示应用,如Typec扩展、手机/电脑投屏、扩展底座、投影仪等。 CS5363管脚分布情况如下: CS5363是一款高度集成的单芯片,适用于多个mGeneral 支持最高分辨率/定时4k60Hz 支持…...

Git Lab 项目迁移到gitee 并且包含提交记录
步骤 1: 准备工作 1.安装Git:确保你在本地计算机上安装了Git。如果尚未安装,可以从Git官网下载并安装。 2.创建Gitee账号:如果你还没有Gitee账号,请先注册一个,访问Gitee官网进行注册。 3.创建新的Gitee仓库࿱…...

如何用用智能码二维码zhinengma.cn做空调机房巡检
用智能码二维码做空调机房巡检 引言 空调机房是保障建筑物内环境舒适度的关键设施,其巡检工作对于确保空调系统的稳定运行至关重要。通过引入智能码二维码技术,可以大大提高空调机房巡检的效率和准确性。 一、二维码在空调机房巡检中的应用 1.1 巡检…...

如何与客户保持高度粘性?这个系统给您答案
客户粘性是企业成功的关键因素之一,企客宝企微版在打通获客、转化、运营全链路方面发挥着重要作用,实现客户粘性的提升。 前言 客户粘性是企业成功的关键因素之一。企业需要不断通过各种手段提升客户粘性,保持客户忠诚度和长期合作关系。企客…...

算法知识点————两个栈实现一个队列
思路:当队列入队的时候,将元素入栈(instack),当队列出栈的时候,先判断栈(outstack)是否为空,如果为空,则将栈(instack)的元素全部放入…...
)
并行程序设计基础——并行I/O(1)
目录 一、概述 1、按照读写定位分类 2、按照同步机制分类 3、按照参加读写操作的进程的限制分类 二、并行文件管理的基本操作 1、MPI_FILE_OPNE 2、MPI_FILE_CLOSE 3、MPI_FILE_DELETE 4、MPI_FILE_SET_SIZE 5、MPI_FILE_PREALLOCATE 6、MPI_FILE_GET_SIZE 7、MPI_…...

在JS中的设计模式的单例模式、策略模式、代理模式、原型模式浅讲
1. 单例模式(Singleton Pattern) 确保一个类只有一个实例,并提供一个全局访问点。 示例代码: class Singleton {constructor() {if (Singleton.instance) {return Singleton.instance;}Singleton.instance this;this.data []…...
JVM系列(十) -垃圾收集器介绍
一、摘要 在之前的几篇文章中,我们介绍了 JVM 内部布局、对象的创建过程、运行期的相关优化手段以及垃圾对象的回收算法等相关知识。 今天通过这篇文章,结合之前的知识,我们一起来了解一下 JVM 中的垃圾收集器。 二、垃圾收集器 如果说收集算法是内存回收的方法论,那么…...
---UI与上层service的交互优化)
项目实战 ---- 商用落地视频搜索系统(9)---UI与上层service的交互优化
目录 背景 第一次优化(UI优化) 优化前UI 优化方向与问题 代码 修改效果 第二次优化(整合优化) 优化方向与问题 代码 优化效果 第三次优化(js层优化) 优化方向与问题 代码 优化效果 第四次优化(UI逻辑再优化) 优化方向与问题 代码 优化效果 第五次优化(纯U…...

媒体服务器软件BUG说明及改进方案
媒体服务器软件BUG说明及改进方案 一、BUG描述二、问题分析三、改进方案四、实施计划五、预期效果六、总结一、BUG描述 在当前版本的媒体服务器中,存在一个关于静音媒体流处理的问题。具体表现为:当主叫连续发送静音帧到媒体服务器时,媒体服务器并未将这些静音帧转发给被叫…...

Gitlab修改已push的历史commit信息
文章目录 一、需求 二、思路 三、修改过程 四、注意 五、参考链接 一、需求 项目组结合使用JIRA和Gitlab进行项目开发。其中,JIRA用于管理开发任务(每个任务都存在一个JIRA_ID),Gitlab用于进行代码版本管理。每次代码提交时,commit mes…...

[Linux入门]---进程替换
文章目录 1.进程替换原理2.进程替换函数2.1execl函数2.2execlp函数2.3execv函数2.4execvp函数2.5execle函数2.6execve函数2.7跨语言调用程序 3.总结 1.进程替换原理 一个程序替换的函数: #include <unistd.h> int execl(const char *path, const char *arg,…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...
