LeetCode:322. 零钱兑换——动态规划从案例入门
🌻算法,不如说它是一种思考方式🍀
算法专栏: 👉🏻123
一、🌱322. 零钱兑换
-
题目描述:给你一个整数数组coins,表示不同面额的硬币;以及一个整数 amount,表示总金额。计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回-1。你可以认为每种硬币的数量是无限的。
-
来源:力扣(LeetCode)
-
难度:中等
-
提示:
1 <= coins.length <= 12
1 <= coins[i] <= 231 - 1
0 <= amount <= 104 -
示例 1:
输入:coins = [1, 2, 5], amount = 11
输出:3
解释:11 = 5 + 5 + 1
示例 2:
输入:coins = [2], amount = 3
输出:-1
示例 3:
输入:coins = [1], amount = 0
输出:0
🌾动态规划
动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其他的算法。
- 先不考虑动态规划来看这道题:就是求解一个最优组合使得最少个数达到总金额目标。
我们最容易想到就是去暴力求解,就是找出所有合适的组合,确定一个最小的。以示例1来看【coins = [1, 2, 5], amount = 11】,3个硬币那我们套三层循环,总可以遍历出来的。但是当这个amout非常大呢、硬币数量非常多的时候,这总时间开销会非常大,指数级别了。 - 那么这时候换一个思路:我们要求出最后完成amout,那我们看最后一枚硬币假如是ck,这个ck就会有3种可能取值:1,2,5。
假如我们设置一个函数来求解最少需要用多少枚硬币凑出x:f(x)。
那么当ck=1,f(11)=f(10)+1;——就是当最后一枚硬币是1,那我们就要进一步求如何最小的凑出10;
那么当ck=2,f(11)=f(9) + 1;——就是当最后一枚硬币是2,那我们就要进一步求如何最小的凑出9;
那么当ck=5,f(11)=f(6) + 1;——就是当最后一枚硬币是5,那我们就要进一步求如何最小的凑出6;
这时候我们发现上面就是:f(11)=min{f(10)+1,f(9) + 1,f(6) + 1},后面也是类似的过程,于是我们可以写出一个递归实现的方法:跳转到递归实现。👇🏻 - 但是递归实现仍然时间复杂度太高,我们继续上面的推一下就会发现,里面存在大量重复计算,例如在计算f(10)又会出现f(9)…
还是对于f(11)=min{f(10)+1,f(9) + 1,f(6) + 1},我们可以写为f(x)=min{f(x-1)+1,f(x-2) + 1,f(x-5) + 1}。我们把f看为数组,把每一个amout看为下标,
❶amount当然不能小于0,那小于0的暂设置为无穷大吧,
❷f(0)就代表凑0元,那么就只有0枚,
❸f(1)就代表凑1元,根据f(x),计算是1
…
| 0 | 1 | 2 | 3 | … |
|---|---|---|---|---|
| 0 | 1 | 1 | 2 | … |
这样计算方程的时候,后面的直接使用数组前面已计算的,就不会造成重复计算了。
上面的过程我们就完成了确定状态、状态转移方程、初始化、递推求解。跳转到动态规划实现。👇🏻
动态规划算法思想
通常用于解决具有重叠子问题和最优子结构性质的问题。动态规划算法的思想是将原问题拆解成若干个子问题,通过求解子问题的最优解来求解原问题的最优解。
动态规划算法一般分为以下几个步骤:
- 确定状态:将原问题拆解成若干个子问题,确定状态,状态表示的是原问题和子问题中的变量。
- 确定状态转移方程:根据子问题和原问题之间的关系,确定状态转移方程,状态转移方程表示的是子问题之间的关系。
- 初始化:确定初始状态,即最小的子问题的解。
- 递推求解:按照状态转移方程,从初始状态开始逐步求解子问题,直到求解出原问题的最优解。
动态规划算法的优点是可以避免重复计算,大大提高了算法的效率。动态规划算法可以解决很多问题,如最长公共子序列、背包问题、最短路径问题等。
状态转移方程
状态转移方程是动态规划算法的核心,是求解最优子结构问题的重要手段。其实质是将问题从大到小分解为若干个子问题,然后根据子问题之间的关系,通过递推的方式求解出原问题的最优解。
状态转移方程的一般形式为:
dp[i] = f(dp[i-1], dp[i-2], ..., dp[0])
其中,dp[i]表示原问题中规模为i的问题的解,f为求解dp[i]的函数,dp[0]到dp[i-1]表示规模比i小的子问题的解。状态转移方程的求解需要满足以下条件:
- 问题具有最优子结构性质,即原问题的最优解可以由子问题的最优解递推得到。
- 问题具有重叠子问题性质,即子问题之间存在重叠,同一个子问题可能被多次求解。
状态转移方程的求解通常需要一定的数学分析能力和算法设计能力,需要根据问题的特点和规模,选择合适的递推方式和边界条件,确保算法的正确性和高效性。常见的状态转移方程包括斐波那契数列、最长公共子序列、背包问题等,这些问题的状态转移方程都具有简单明了的形式和良好的递推性质,是动态规划算法的经典例题。
- 以斐波那契数列(从第三项开始,每一项都等于前两项之和)为例,其状态转移方程为:
f(n) = f(n-1) + f(n-2)(n >= 2)
其中,f(n)表示第n个斐波那契数;f(n-1)表示第n-1个斐波那契数;f(n-2)表示第n-2个斐波那契数。根据状态转移方程,我们可以通过求解第n-1个和第n-2个斐波那契数来求解第n个斐波那契数,从而计算出整个斐波那契数列。在这个例子中,状态转移方程描述了一个状态如何从前面的状态转移而来,即第n个斐波那契数等于前两个斐波那契数的和。
在实际应用中,状态转移方程是根据问题的具体特点而确定的,通常需要对问题进行抽象和分析,确定问题的状态和状态之间的关系,才能得到正确的状态转移方程。
背包问题
有一个容量为capacity的背包和n个物品,每个物品有一个重量和一个价值,要求选择一些物品放入背包中,使得背包的总重量不超过容量,且所选物品的总价值最大。
用动态规划算法求解:
public class KnapsackProblem {public static void main(String[] args) {int[] weights = {2, 2, 6, 5, 4};int[] values = {6, 3, 5, 4, 6};int capacity = 10;int maxValue = knapsack(weights, values, capacity);System.out.println("The maximum value is: " + maxValue);}public static int knapsack(int[] weights, int[] values, int capacity) {int n = weights.length;int[][] dp = new int[n + 1][capacity + 1];for (int i = 1; i <= n; i++) {for (int j = 1; j <= capacity; j++) {if (weights[i - 1] <= j) {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1]);} else {dp[i][j] = dp[i - 1][j];}}}return dp[n][capacity];}
}
时间复杂度为O(n×capacity),空间复杂度为O(n×capacity)。
🌴解题
1.直接递归(超时)
- code:
class Solution {public int coinChange(int[] coins, int amount) {int ans=mcoinChange(coins,amount);return ans==10000?-1:ans;}public static int mcoinChange(int[] coins, int amount) {if(amount==0)return 0;int res=10000;for (int i = 0; i < coins.length; i++) {if (amount >= coins[i]) {res = Math.min(mcoinChange(coins, amount - coins[i]) + 1, res);}}return res;}
}
2.动态规划
对于一个状态方程我们可以使用for循环进行展开:for (int j = 0; j < coins.length; j++)。
- code:
class Solution {public int coinChange(int[] coins, int amount) {if(amount==0)return 0;int res=1000000;int[] ans=new int[amount+1];ans[0]=0;//初始for (int i = 1; i <= amount; i++) {int temp=res;for (int j = 0; j < coins.length; j++) {if(i-coins[j]<0)continue;temp= Math.min(ans[i-coins[j]]+1,temp);}ans[i]=temp;}return ans[amount]==res?-1:ans[amount];}
}

返回第一页。☝
☕物有本末,事有终始,知所先后。🍭
🍎☝☝☝☝☝我的CSDN☝☝☝☝☝☝🍓
相关文章:

LeetCode:322. 零钱兑换——动态规划从案例入门
🍎道阻且长,行则将至。🍓 🌻算法,不如说它是一种思考方式🍀算法专栏: 👉🏻123 一、🌱322. 零钱兑换 题目描述:给你一个整数数组coins,…...
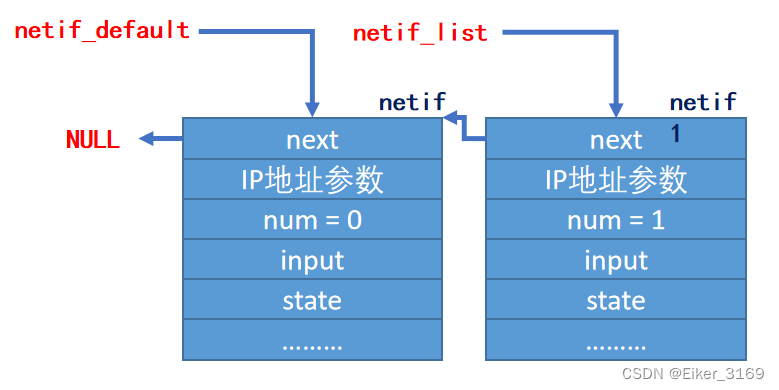
【lwIP(第四章)】网络接口
目录一、lwIP网络接口简介二、lwIP的netif结构三、lwIP的netif相关函数1. lwIP网络接口的全局变量2. netif_add()函数3. netif_remove()函数4. netif_set_default()函数一、lwIP网络接口简介 lwIP协议栈支持多种不同的网络接口(网卡),由于网卡…...

Vue3 pinia入门篇(一)
系列文章目录 主要为了记录如何使用Pinia在Vue3中的使用方式(下面会介绍为什么使用Vue3选型) 文章目录系列文章目录不用Vue2使用Pinia举例子?1.笔者的个人看法:2.总结一、Pinia是什么1.状态管理工具(类比Vuexÿ…...

python面向对象编程解释
python是一个面向对象的编程语言 面向过程的开发语言有C,面向对象除了python还有java等语言 具体来讲: 面向过程 :举个例子,比如说,把大象装进冰箱总共分几步,第一步,把冰箱门打开,…...
ARM(IMX6U)嵌入式软件裸机开发之环境搭建与配置
目录 前沿 Ubuntu 和 Windows 文件互传 Ubuntu 下 NFS 和 SSH 服务开启 Ubuntu 交叉编译工具链安装 Source Insight 软件安装和使用 Visual Studio Code 软件的安装和使用 前沿 为什么我们要学习裸机开发呢? 1、裸机开发是了解所使用的 CPU 最直接、最简单的方…...

Java文件复制多种方法
1、InputStream与OutputStream 创建两个文件 - 源和目标。然后我们从源创建InputStream并使用OutputStream将其写入目标文件进行 java 复制文件操作。 private static void copyFileUsingStream(File source, File dest) throws IOException {InputStream is null;OutputStr…...
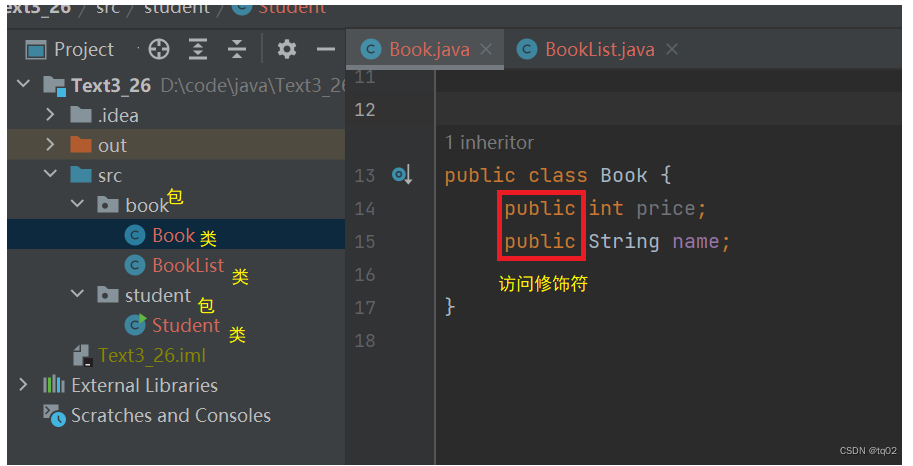
Java语言-----封装、继承、抽象、多态、接口
目录 前言 一.封装 1.1封装的定义 1.2访问修饰符的使用 二.继承 2.1继承的定义 2.2继承的方法 2.3继承使用注意点 三.多态 3,1多态的定义 3.2动态绑定 3.3方法重写 3.4向上(向下)转型 四.抽象 4.1抽象的概述和定义 4.2抽象的使用 五…...
基于深度学习的瓶子检测软件(UI界面+YOLOv5+训练数据集)
摘要:基于深度学习的瓶子检测软件用于自动化瓶子检测与识别,对于各种场景下的塑料瓶、玻璃瓶等进行检测并计数,辅助计算机瓶子生产回收等工序。本文详细介绍深度学习的瓶子检测软件,在介绍算法原理的同时,给出Python的…...
仿网易云小程序(一)
目录 一、项目准备 二、项目初始化 1.新建项目 2.封装service请求 三、底部导航栏的设计 四、MV页面的设计 1.将获取到的数据进行渲染 2.播放量数据进行处理转换 3.时长数据进行处理转换 五、MV组件的抽离封装 六、请求的抽离video 七、下拉重新请求新的数据 八、跳转到…...
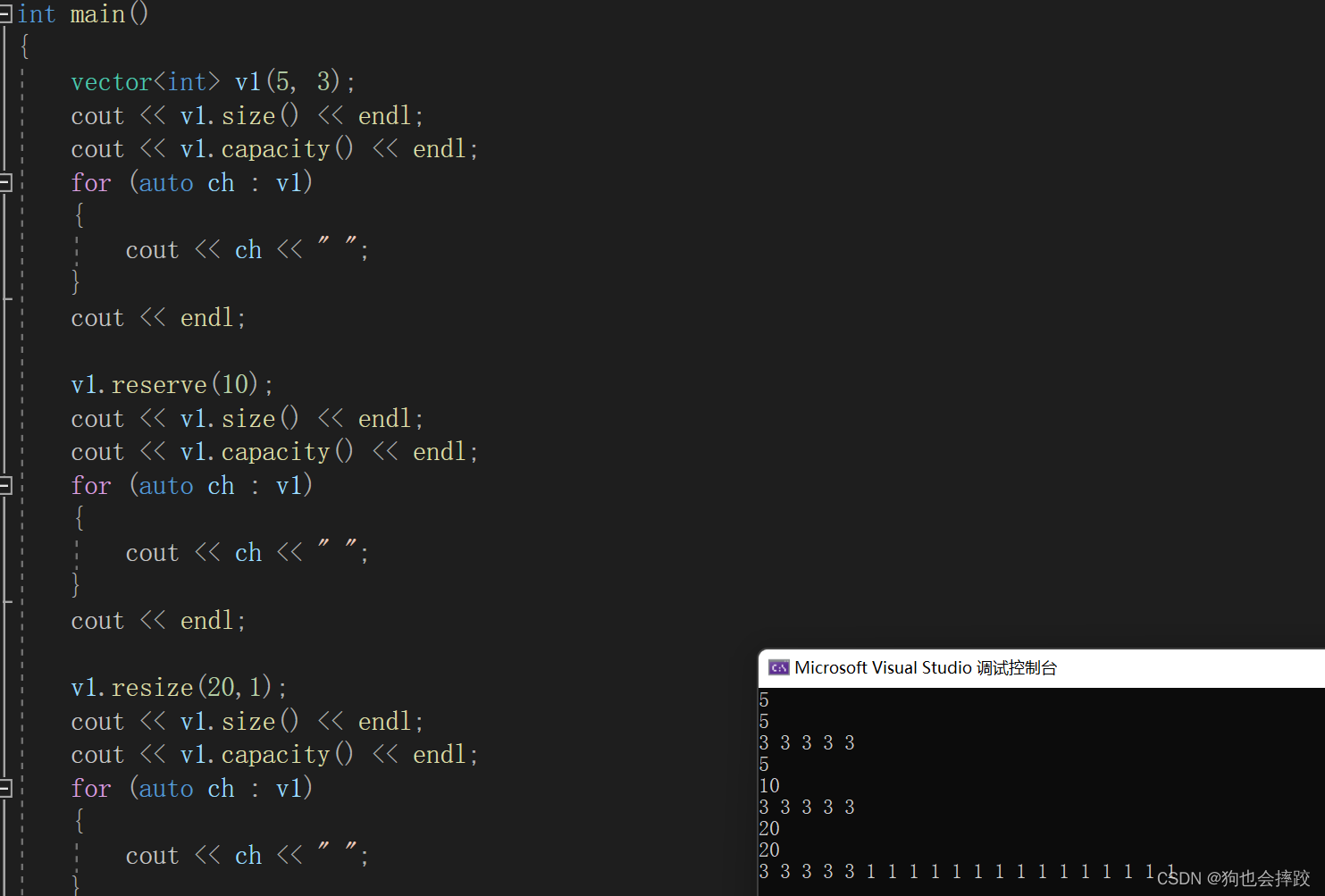
【C++】vector模拟实现及其应用
文章目录vector的介绍vector的使用及其实现vector的定义vector iterator 的使用vector空间增长问题vector的增删查改vector的介绍 vector是表示可变大小数组的序列容器。就像数组一样,vector也采用的连续存储空间来存储元素。也就是意味着可以采用下标对vector的元素…...

JS看这一篇就够啦,JS基础大全,可用于快速回顾知识,面试首选
1 JS简介 更多JS内容可以看MDN:点击传送 浏览器分成两部分:渲染引擎和 JS 引擎 渲染引擎:用来解析HTML与CSS,俗称内核,比如 chrome 浏览器的 blink ,老版本的 webkitJS 引擎:也称为 JS 解释器…...

武汉凯迪正大GB4208外壳防护等级试具
一、IP1X 试验探棒 产品概述: 符合IEC61032图1试具A、GB16842试具A、GB4208IP1、IEC60529IP1、IEC60065 等标准要求。用于防止手背触及的防护检验。 技术参数: 1、探球直径:50mm 2、挡板直径:45mm 3、挡板厚度:…...

Cent OS 从零部署ruoyi-cloud教程
1、java环境安装 https://blog.csdn.net/m0_61035257/article/details/125705400 Java_home设置 https://blog.csdn.net/m0_51104427/article/details/123924893 2、mysql安装 https://blog.csdn.net/ShockChen7/article/details/126965940 若安装的是Mysql8,建议…...

ChatGPT相关核心算法
ChatGPT 的卓越表现得益于其背后多项核心算法的支持和配合。本文将分别介绍作为其实现基础的 Transformer 模型、激发出其所蕴含知识的Prompt/Instruction Tuning 算法、其涌现出的思维链能力、以及确保其与人类意图对齐的基于人类反馈的强化学习算法。 1.基于Transformer的预…...
)
Python导入模块,Python import用法(超级详细)
使用 Python 进行编程时,有些功能没必须自己实现,可以借助 Python 现有的标准库或者其他人提供的第三方库。比如说,在前面章节中,我们使用了一些数学函数,例如余弦函数 cos()、绝对值函数 fabs() 等,它们位…...

大量产品“GPT 化”,开源大模型 AI 应用开发框架发布
大型语言模型(LLM)的出现,让我们看到了 AI 在自然语言处理方面的潜力,它涌现出来的创造力和思维能力令人叹为观止,并在新一代人机交互领域释放了大量的想象空间。 目前,决策者、产品负责人和开发者都在抢滩…...
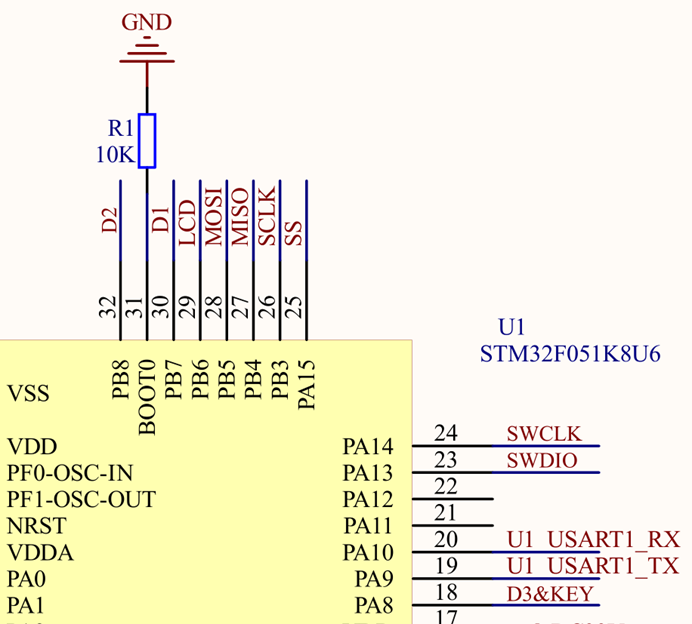
STM32——IIC总线(MPU6050应用)
目录 一、IIC介绍 二、MPU6050 三、MPU6050实例 四、EEPROM ---------------------------------------------------------------------------------------------------------------------------- 每次都是IIC好没新意啊,我决定这次录视频的时候举两个例子&…...

ADB使用经验
adb是Android Debug Bridge的缩写,是一种用于与Android设备通信的命令行工具。它可以通过USB连接或Wi-Fi连接,允许开发者在计算机和Android设备之间进行文件传输、安装应用程序、调试应用程序等操作。要使用adb,需要先将Android设备与计算机连…...
详解LinkedHashSet和LinkedHashMap
目录 一.LinkedHashSet和LinkedHashMap 1.基本介绍 2.与HashSet和HashMap的区别 3.LinkedHashSet和LinkedHashMap具体的方法 1.LinkedHashSet 2.LinkedHashMap 二.模拟代码实现LinkedHashMap 三.具体应用 一.LinkedHashSet和LinkedHashMap 1.基本介绍 顾名思义,根据名…...
C++ LinuxWebServer 2万7千字的面经长文(下)
⭐️我叫忆_恒心,一名喜欢书写博客的在读研究生👨🎓。 如果觉得本文能帮到您,麻烦点个赞👍呗! Linux Web Server项目虽然是现在C求职者的人手一个的项目,但是想要吃透这个项目,还是…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
