备战秋招60天算法挑战，Day34

题目链接： https://leetcode.cn/problems/coin-change/

视频题解： https://www.bilibili.com/video/BV1qsvDeHEkg/

LeetCode 322.零钱兑换

题目描述

给你一个整数数组coins，表示不同面额的硬币；以及一个整数amount，表示总金额。

计算并返回可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回-1 。

你可以认为每种硬币的数量是无限的。

举个例子：

输入： coins = [1, 2, 5], amount = 11
输出： 3 
解释： 11 = 5 + 5 + 1

视频题解

零钱兑换

思路来源

思路来源

知识回顾

动态规划是一种通过将原问题分解为子问题来求解复杂问题的算法思想。它通常用于求解最优化问题，例如最长公共子序列、背包问题等。动态规划的核心思想是将原问题分解为若干个子问题，通过求解子问题的最优解推导出原问题的最优解。可以通过两点来判断一个问题能不能通过动态规划来解，一是该问题是否存在递归结构，二是对应的子问题能否记忆化。动态规划可以通过带备忘录的自上而下的递归和自下而上的迭代来分别实现。由于递归需要用到栈来实现，一些语言对递归的深度是有限制的，所以自下而上的迭代是动态规划的最佳实现方式。

思路解析

根据题意，零钱兑换的决策树如下图:

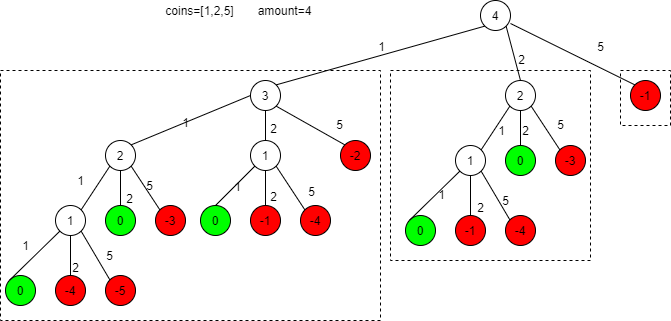
根节点表示要兑换的总金额amount，每个子节点表示amount已经兑换了coins[i]（对于图中的例子0 <= i < 3）以后剩余要兑换的钱。叶子结点为0表示从根节点到叶子结点这条兑换路径是行得通的，叶子结点为负数表示行不通。

实际上本题就是要求在这棵树上所有行得通的兑换路径中，寻找最短合法路径的长度。

整个决策树存在递归结构，还存在重复子问题两个节点2、三个节点1，这些子问题计算一次后可以直接保存下来，避免多次重复计算。这就满足了使用动态规划的条件：存在递归结构和子问题可以记忆化。所以本题可以用动态规划来解。动态规划可以通过带备忘录的自上而下的递归和自下而上的迭代来分别实现。

方法一 自上而下的递归+备忘录

本题单纯的使用递归会超时的。

通过观察上图，可以看出每个分支存在很多相同的子问题，比如兑换总金额2元，兑换总金额1元。我们可以在递归的过程中使用备忘录把这些子问题的结果保存起来，后面就作为跳出递归的一个条件，这样可以大大节约时间。

C++代码

class Solution {
public:int coinChange(vector<int> &coins, int amount) {//定义备忘录vector<int> count(amount + 1, INT_MAX);count[0] = 0;int res = help(coins, count, amount);return res;
}int help(vector<int> &coins, vector<int>& count, int amount) {//如果备忘录中已经保存结果if (count[amount] < INT_MAX - 1) {//直接返回return count[amount];}int coins_len = coins.size();int min_res = INT_MAX;for (int i = 0; i < coins_len; ++i) {if (amount - coins[i] >= 0) {//递归遍历（DFS）所以的可能性int res = help(coins, count, amount - coins[i]);if (res >= 0 && res < min_res) {min_res = res + 1;}}}//更新备忘录count[amount] = min_res == INT_MAX ? -1 : min_res;//返回结果return count[amount];
}};

java代码

class Solution {public int coinChange(int[] coins, int amount) {// 定义备忘录int[] count = new int[amount + 1];Arrays.fill(count, Integer.MAX_VALUE);count[0] = 0;int res = help(coins, count, amount);return res;}private int help(int[] coins, int[] count, int amount) {// 如果备忘录中已经保存结果if (count[amount] < Integer.MAX_VALUE - 1) {// 直接返回return count[amount];}int min_res = Integer.MAX_VALUE;for (int coin : coins) {if (amount - coin >= 0) {// 递归遍历（DFS）所有的可能性int res = help(coins, count, amount - coin);if (res >= 0 && res < min_res) {min_res = res + 1;}}}// 更新备忘录count[amount] = (min_res == Integer.MAX_VALUE) ? -1 : min_res;// 返回结果return count[amount];}
}

python代码

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:# 定义备忘录count = [float('inf')] * (amount + 1)count[0] = 0res = self.help(coins, count, amount)return resdef help(self, coins, count, amount):# 如果备忘录中已经保存结果if count[amount] < float('inf') - 1:# 直接返回return count[amount]min_res = float('inf')for coin in coins:if amount - coin >= 0:# 递归遍历（DFS）所有的可能性res = self.help(coins, count, amount - coin)if res >= 0 and res < min_res:min_res = res + 1# 更新备忘录count[amount] = -1 if min_res == float('inf') else min_res# 返回结果return count[amount]

复杂度分析

时间复杂度： 时间复杂度为O(mn)，其中m为coins中元素的个数，n为要兑换的总金额。

空间复杂度： 空间复杂度为O(n)，n为要兑换的总金额。

方法二 自下而上的迭代

实现自下而上而上迭代的两个关键步骤：确定状态转移公式和边界情况。

首先定义dp[i]表示兑换金额为i，使用coins中的零钱兑换所需最少的个数。dp[i]的准确定义是状态转移公式成功推导的关键。

针对coins = [1, 2, 5]，amount = 4。从上面的决策树可以看出可以把兑换4块钱分解成兑换3元，兑换2元，兑换-1元，三个子问题。其中-1元是无法兑换的，可以直接把这个分支剪掉。可以得到下面的公式：

dp[4] = min{dp[3], dp[2]} + 1

类似地，把amount = 4扩展到amount = n，可以得到如下状态转移公式：

dp[n] = min{dp[n-coins[0]], dp[n-coins[1]], ..., dp[n-coins[m-1]]} + 1

其中m为coins的大小，且需要n - coins[i] >= 0，0 <= i < m​。

接下来看一下边界情况，题目中已经说明amount = 0时对应的兑换个数为0，所以dp[0] = 0。

C++代码

class Solution {
public:int coinChange(vector<int> &coins, int amount) {int coins_len = coins.size();//因为dp是从0开始，要兑换总金额为amount，所以要申请amount+1个元素vector<int> dp(amount + 1, amount + 1);//边界处理dp[0] = 0;for (int i = 1; i <= amount; ++i) {for (int j = 0; j < coins_len; ++j) {//剪掉节点为负的情况if (i - coins[j] >= 0) {//状态转移公式dp[i] = min(dp[i], dp[i-coins[j]] + 1);}}}return dp[amount] == amount + 1 ? -1: dp[amount];}
};

java代码

class Solution {public int coinChange(int[] coins, int amount) {int coins_len = coins.length;// 因为dp是从0开始，要兑换总金额为amount，所以要申请amount+1个元素int[] dp = new int[amount + 1];Arrays.fill(dp, amount + 1);// 边界处理dp[0] = 0;for (int i = 1; i <= amount; i++) {for (int j = 0; j < coins_len; j++) {// 剪掉节点为负的情况if (i - coins[j] >= 0) {// 状态转移公式dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);}}}return dp[amount] == amount + 1 ? -1 : dp[amount];}
}

python代码

class Solution:def coinChange(self, coins: List[int], amount: int) -> int:coins_len = len(coins)# 因为dp是从0开始，要兑换总金额为amount，所以要申请amount+1个元素dp = [amount + 1] * (amount + 1)# 边界处理dp[0] = 0for i in range(1, amount + 1):for j in range(coins_len):# 剪掉节点为负的情况if i - coins[j] >= 0:# 状态转移公式dp[i] = min(dp[i], dp[i - coins[j]] + 1)return -1 if dp[amount] == amount + 1 else dp[amount]

复杂度分析

时间复杂度： 时间复杂度为O(m*n)，其中m为coins中元素的个数，n为要兑换的总金额。

空间复杂度： 空间复杂度为O(n)，n为要兑换的总金额。