Numpy中数组的形状处理
目录
- 将多维数组降为一维数组
- 竖直方向或水平方向数组的堆叠
数组形状处理的手段主要有reshape,resize,ravel,flatten,vstack,hstack,row_stack,column_stack,下面通过简单
的案例来解释这些方法或函数的区别。
import numpy as np
arr2=np.array([[1,5,7],[3,6,1],[2,4,8],[5,8,9]])
#使用reshape方法更改数组的形状
print(arr2.reshape(4,3))
#打印arr2的形状
print(arr2.shape)#使用resize的方法改变数组的形状
print(arr2.resize(4,3))
#打印arr2的形状
print(arr2.shape)[[1 5 7][3 6 1][2 4 8][5 8 9]]
(4, 3)
None
(4, 3)结论:
1.reshape方法只是返回改变形状的预览,但未真正改变数组的形状;
2.resize方法则不会返回预览,而会直接改变数组的形状
将多维数组降为一维数组
利用ravel,flatten和reshape三种方法均可解决;
import numpy as np
arr2=np.array([[1,5,7],[3,6,1],[2,4,8],[5,8,9]])
print(arr2)
#默认排序降维
print(arr2.ravel())
print(arr2.flatten())
print(arr2.reshape(-1))
# 改变排序模式的降维
print(arr2.ravel(order ='F'))
print(arr2.flatten(order ='F'))
print(arr2.reshape(-1,order ='F'))[[1 5 7][3 6 1][2 4 8][5 8 9]]
[1 5 7 3 6 1 2 4 8 5 8 9]
[1 5 7 3 6 1 2 4 8 5 8 9]
[1 5 7 3 6 1 2 4 8 5 8 9]
[1 3 2 5 5 6 4 8 7 1 8 9]
[1 3 2 5 5 6 4 8 7 1 8 9]
[1 3 2 5 5 6 4 8 7 1 8 9]对降维后的数组进行元素修改,看是否会影响到原数组arr4的变化;
import numpy as np
arr2=np.array([[1,5,7],[3,6,1],[2,4,8],[5,8,9]])
arr2.flatten()[0]=1000
print(arr2)
arr2.ravel()[1]=2000
print(arr2)
arr2.reshape(-1)[2]=1000
print(arr2)[[1 5 7][3 6 1][2 4 8][5 8 9]]
[[ 1 2000 7][ 3 6 1][ 2 4 8][ 5 8 9]]
[[ 1 2000 1000][ 3 6 1][ 2 4 8][ 5 8 9]]
结论:
1、通过flatten方法实现的降维返回的是复制,因为对降维后的元素做修改,并没有影响到原数组arr4的结果;
2、ravel方法与reshape方法返回的则是视图,通过视图的修改会影响到原数组;
竖直方向或水平方向数组的堆叠
vstack用于垂直方向(纵向)的数组堆叠,其功能与row_stack函数一致;hstack则用于水平方向(横向)的数组合并,其功能与column_stack函数一致;
import numpy as np
arr2=np.array([[1,5,7],[3,6,1],[2,4,8],[5,8,9]])
arr3=np.array([1,2,3])
print(np.vstack(arr2,arr3))
print(np.row_stack(arr2,arr3))print(np.hstack(arr2,arr3))
print(np.column_stack(arr2,arr3))相关文章:

Numpy中数组的形状处理
目录 将多维数组降为一维数组竖直方向或水平方向数组的堆叠 数组形状处理的手段主要有reshape,resize,ravel,flatten,vstack,hstack,row_stack,column_stack,下面通过简单 的案例来解释这些方法…...

【动态规划】子序列问题二(数组中不连续的一段)
子序列问题二 1.最长定差子序列2.最长的斐波那契子序列的长度3.最长等差数列4.等差数列划分 II - 子序列 点赞👍👍收藏🌟🌟关注💖💖 你的支持是对我最大的鼓励,我们一起努力吧!😃&am…...

可视耳勺方便吗?可视耳勺热销第一名品牌!
在生活中,耳部清洁是我们常常会关注却又容易忽视细节的一项日常护理。传统挖耳勺有着不可视的局限性,只能凭感觉和经验反复刮蹭耳朵,很容易将耳垢越捅越深,而且还会刮伤耳道。因此,可视耳勺应运而生,它通过…...

micropython 3-wire spi 9bit 写入的问题
网上猛找把,没有,找不到,mpy不愧是没朋友的缩写,没有咋办,自己造! 此库特别适用那些rgb屏的初始化,大多用3线spi,好家伙rgb用了十多个引脚现在想起来省引脚了是吧,就差这…...

导致JVM内存泄露的ThreadLocal详解
1. ThreadLocal介绍 1.1 什么是ThreadLocal Java官方文档中的描述:ThreadLocal类用来提供线程内部的局部变量。这种变量在多线程环境下访问(通过get和set方法访问)时能保证各个线程的变量相对独立于其他线程内的变量。ThreadLocal实例通常来…...

windows下关闭解除占用端口的进程
环境:windows 10 场景:启动某一应用程序时,提示其他应用已占用此端口,比如端口2425。 解决步骤: 1/3、打开windows的命令提示符,输入以下命令,查找占用此端口2425的PID号: # win…...

Baumer工业相机堡盟工业相机如何通过NEOAPI SDK获取相机当前数据吞吐量(Python)
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK里函数来获取相机当前数据吞吐量(Python) Baumer工业相机Baumer工业相机的数据吞吐量的技术背景CameraExplorer如何查看相机吞吐量信息在NEOAPI SDK里通过函数获取相机接口吞吐量 Baumer工业相机通过NEOAPI…...

版权与开源协议:一场创新与自由的边界之争
在数字时代的浪潮中,版权与开源协议作为知识产权领域的两大支柱,既相互依存又暗自较劲,共同绘制着科技创新的宏伟蓝图。本文将带您深入这场创新与自由的边界之争,探讨版权与开源协议之间的微妙关系,以及它们如何共同推…...

学生用的蓝牙耳机推荐有哪些?实测四款实力出众机型!
在当今数字化学习环境中,学生对蓝牙耳机的需求日益增长,无论是在线课程的学习、图书馆的集中阅读还是日常通勤中的音频资料复习,一款性能优异、舒适度高且价格合理的蓝牙耳机对学生来说至关重要,面对市场上琳琅满目的产品选择&…...
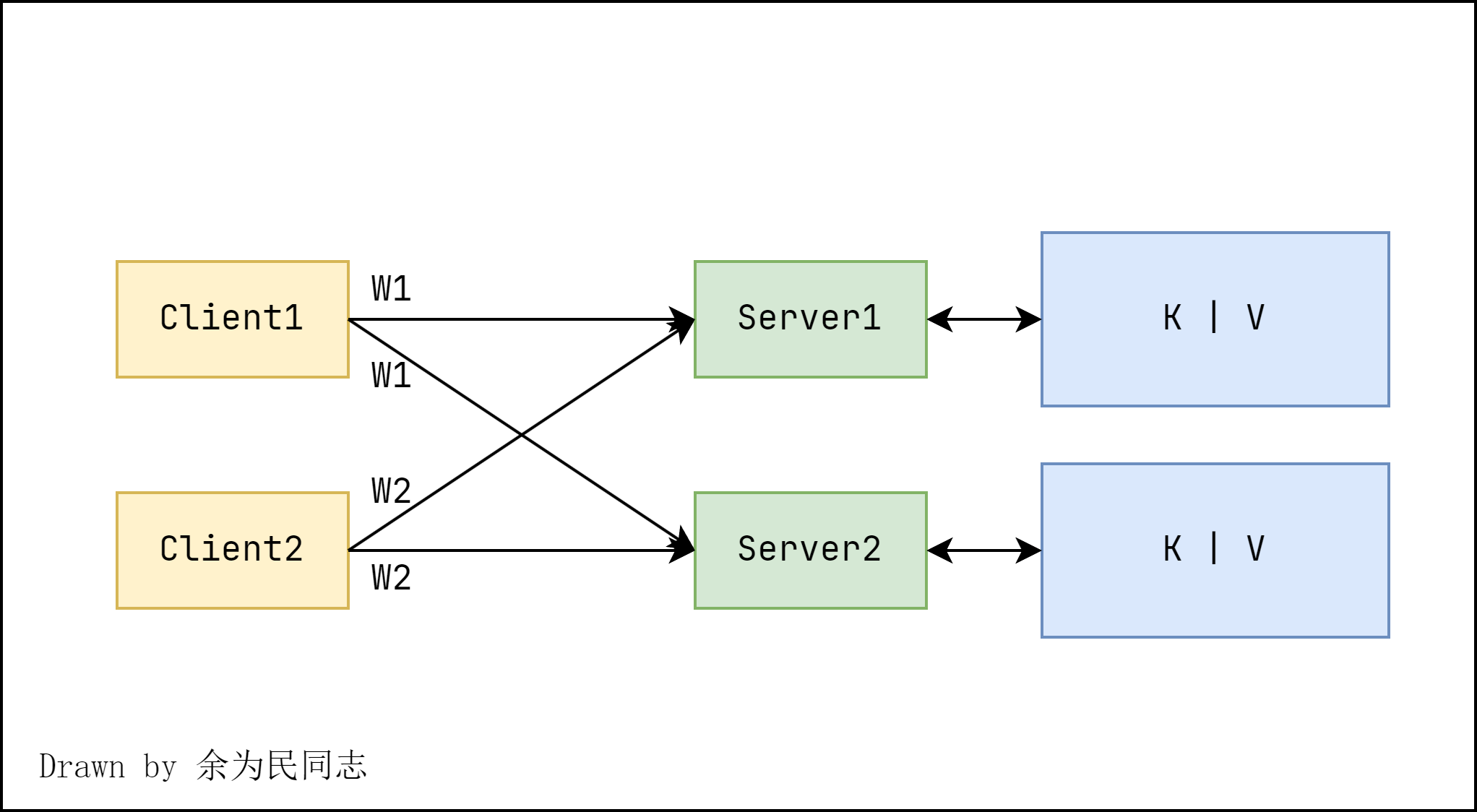
MIT6.824 课程-GFS
GFS 原文:https://zhuanlan.zhihu.com/p/113161014 搬运用于参考学习 概述 存储(Storage)是一个非常关键的抽象,用途广泛。 GFS 论文还提到了很多关于容错、备份和一致性的问题。 GFS 本身是 Google 内部一个很成功的实用系统&…...

力扣第200题 岛屿数量
前言 记录一下刷题历程 力扣第200题 岛屿数量 岛屿数量 原题目: 给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。 岛屿总是被水包围,并且每座岛屿只能由水平…...

协议头,wireshark,http
目录 协议头 ip头 udp头 mac层 网络工具 telnet wireshark Http 一、HTTP 协议介绍 二、HTTP 协议的工作过程 三、使用抓包工具抓取报文 四、获取到http请求报文: 五、http请求(request) (一)、认识URL 项…...

vscode ssh离线远程连接ubuntu调试
遇见问题: 1 ssh连接上无法启动服务器的虚拟环境; 2 ssh连接上启动服务器的虚拟环境后无法打断点; 对于问题需要参考下面连接安装python和debugy的插件拓展,并且配置json文件link。VSCode - 离线安装扩展python插件教程_vscode…...

Jenkins 通过 Version Number Plugin 自动生成和管理构建的版本号
步骤 1:安装 Version Number Plugin 登录 Jenkins 的管理界面。进入 “Manage Jenkins” -> “Manage Plugins”。在 “Available” 选项卡中搜索 “Version Number Plugin”。选中并安装插件,完成后可能需要重启 Jenkins。 步骤 2:配置…...

元学习之应用案例
现在在做元学习的时候,我们最常拿来测 试元学习技术的任务叫做少样本图像分类,简单来讲就是每一个任务都只有几张图片,每一 个类别只有几张图片。比如我们使用图1的案例为例说明。现在分类的任务是分为三个 类别,每个类别都只有两…...

网络高级(学习)2024.9.10
目录 一、Modbus简介 1.起源 2.特点 3.应用场景 二、Modbus TCP协议 1.特点 2.协议格式 3.MBAP报文头 4.功能码 5.寄存器 (1)线圈寄存器,类比为开关量,每一个bit都对应一个信号的开关状态。 (2)…...

【软件全文档】项目概要设计说明书(2024实际项目Word原件)
一、 引言 (一) 编写目的 (二) 范围 (三) 文档约定 (四) 术语 二、 项目概要 (一) 建设背景 (二) 建设目标 (三࿰…...

震惊!国产数据库厂商减少了51家!
前面文章我提到国产数据库厂商实际上大部分都不赚钱,我估计国产目前国产数据库厂商利润为正的,目前不超过5家。 而经济寒冬,融资困难,那么对于很多厂商,尤其是全靠融资的数据库厂商来讲,这将变得极其困难。…...

[AI书籍分享]<AI时代,学什么,怎么学 - 和渊>
本文由Markdown语法编辑器编辑完成。 1, 背景: 本书是一位清华大学毕业的生物学博士,和渊老师,现就职于人大附中, 是一名一线的高中生物教师. 她之前已经写过几本关于教育类的书籍,而这本书,则是她针对当前, AI时代迅猛发展的背…...

鸿蒙HarmonyOS开发:一次开发,多端部署(界面级)断点和媒体查询
文章目录 概述引入与使用流程媒体查询条件语法规则媒体类型(media-type)媒体逻辑操作(media-logic-operations)媒体特征(media-feature) 场景示例1、监听设备屏幕的方向(竖屏,横屏&a…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
