代码随想录训练营 Day57打卡 图论part07 53. 寻宝（prim，kruskal算法）

代码随想录训练营 Day57打卡 图论part07

卡码53. 寻宝

题目描述
在世界的某个区域，有一些分散的神秘岛屿，每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路，方便运输。
不同岛屿之间，路途距离不同，国王希望你可以规划建公路的方案，如何可以 以最短的总公路距离 将所有岛屿联通起来（注意：这是一个无向图）。
给定一张地图，其中包括了所有的岛屿，以及它们之间的距离。以最小化公路建设长度，确保可以链接到所有岛屿。
输入描述
第一行包含两个整数V 和 E，V代表顶点数，E代表边数 。顶点编号是从1到V。例如：V=2，一个有两个顶点，分别是1和2。
接下来共有 E 行，每行三个整数 v1，v2 和 val，v1 和 v2 为边的起点和终点，val代表边的权值。
输出描述
输出联通所有岛屿的最小路径总距离
输入示例
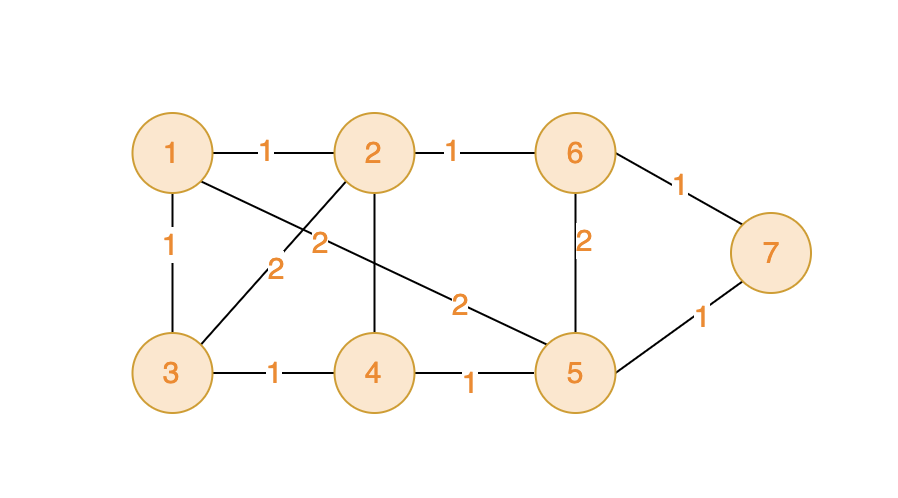
7 11
1 2 1
1 3 1
1 5 2
2 6 1
2 4 2
2 3 2
3 4 1
4 5 1
5 6 2
5 7 1
6 7 1
输出示例
6
提示信息
数据范围：
2 <= V <= 10000;
1 <= E <= 100000;
0 <= val <= 10000;
如下图，可见将所有的顶点都访问一遍，总距离最低是6.

版本一 prim算法

这是一个典型的 Prim算法 问题，目的是找到图的最小生成树（MST），即连接所有节点的总边权值最小的树。

def prim(v, e, edges):# 初始化一个 v+1 * v+1 的邻接矩阵，初始值为一个很大的数grid = [[float('inf')] * (v + 1) for _ in range(v + 1)]# 读取所有边的信息，构建邻接矩阵for x, y, k in edges:grid[x][y] = kgrid[y][x] = k# 最小生成树中每个节点与其他树节点的最小距离minDist = [float('inf')] * (v + 1)# 标记节点是否在最小生成树中isInTree = [False] * (v + 1)# 从第一个节点开始，设定它的初始距离为0minDist[1] = 0# 最小生成树的权值总和result = 0# Prim算法，执行 v-1 次，选择 v-1 条边构造最小生成树for _ in range(1, v):  # v-1次cur = -1  # 当前选中要加入树的节点minVal = float('inf')# 第一步：选择离生成树最近的节点for j in range(1, v + 1):if not isInTree[j] and minDist[j] < minVal:minVal = minDist[j]cur = j# 第二步：将选中的节点加入最小生成树isInTree[cur] = Trueresult += minVal# 第三步：更新所有非生成树节点到生成树的最小距离for j in range(1, v + 1):if not isInTree[j] and grid[cur][j] < minDist[j]:minDist[j] = grid[cur][j]return result# 读取输入
v, e = map(int, input().split())  # v 为节点数，e 为边数
edges = []
for _ in range(e):x, y, k = map(int, input().split())edges.append((x, y, k))# 调用 Prim 算法并输出结果
print(prim(v, e, edges))

1. 邻接矩阵：我们用 grid 来表示邻接矩阵，初始值为 float(‘inf’)，表示两个节点之间没有边连接。对于每个输入的边 (x,
   y, k)，我们设置 grid[x][y] = k 和 grid[y][x] = k，因为这是一个无向图。
2. minDist 数组：该数组用于存储每个节点到已加入最小生成树的最近距离，初始值为 float(‘inf’)，表示未与最小生成树相连。
3. isInTree 数组：该数组用于记录每个节点是否已经被加入最小生成树。
4. Prim算法：我们进行 v-1次迭代，每次选择一个离当前生成树最近的节点，加入最小生成树，并更新所有未加入树的节点与当前生成树的最小距离。
5. 结果计算：在每次迭代时，将选中的边的权值加到最终结果 result 中，最后返回最小生成树的权值总和。

时间复杂度：

• 构建邻接矩阵：时间复杂度是 O(v^2)，因为我们存储了所有节点对之间的边。
• 主循环：由于每次我们都需要遍历 v 个节点，寻找最近的节点，因此每次循环的复杂度为 O(v)，总的时间复杂度为 O(v^2)。

版本二 kruskal算法

Kruskal算法是一种贪心算法，它的目标是通过选择最小的边来构建最小生成树。Kruskal算法的核心思想是维护边的集合，而不是像Prim算法那样维护节点的集合。

Kruskal算法的步骤：

1. 边权排序：首先对所有的边按权值从小到大排序，因为我们要优先选择权值最小的边。
2. 并查集判断：遍历每条边，判断它连接的两个节点是否已经属于同一个集合（即是否已经连通）。如果两个节点属于同一个集合，添加这条边将形成环路，应该跳过这条边；如果两个节点不属于同一个集合，就可以添加这条边，并将两个节点合并到同一个集合。
3. 结束条件：当我们选择了 n-1 条边时（其中 n 是图中的节点数），生成树构建完毕。

Kruskal算法的关键数据结构是并查集（Union-Find），并查集可以帮助我们高效地判断两个节点是否已经连通。

Kruskal算法的关键点：

• 并查集：用于维护节点的集合关系，主要支持两个操作：

  Find：查找某个节点所在集合的根节点，使用路径压缩加速查找。
  Union：将两个节点所在的集合合并。

• 边权排序：对所有的边按权值从小到大排序，以贪心策略构建最小生成树。

class Edge:def __init__(self, l, r, val):self.l = l  # 边的左端点self.r = r  # 边的右端点self.val = val  # 边的权值# 节点的最大数量假设为 10001
n = 10001
father = list(range(n))  # 并查集的父节点数组，初始时每个节点的父节点都是它自己# 初始化并查集
def init():global fatherfather = list(range(n))# 并查集的查找操作，使用路径压缩优化
def find(u):if u != father[u]:father[u] = find(father[u])  # 路径压缩，将节点 u 直接指向根节点return father[u]# 并查集的合并操作，将节点 u 和节点 v 所在的集合合并
def join(u, v):u = find(u)v = find(v)if u != v:father[v] = u  # 将 v 的根节点指向 u 的根节点# Kruskal算法，求最小生成树的权值总和
def kruskal(v, edges):edges.sort(key=lambda edge: edge.val)  # 将边按权值从小到大排序init()  # 初始化并查集result_val = 0  # 最小生成树的权值总和edge_count = 0  # 记录已经加入生成树的边数# 遍历排序后的边for edge in edges:if edge_count == v - 1:  # 如果已经选择了 v-1 条边，生成树构建完毕break# 查找边的两个端点的根节点x = find(edge.l)y = find(edge.r)# 如果两个端点不属于同一个集合，说明可以加入最小生成树if x != y:result_val += edge.val  # 累加边的权值join(x, y)  # 合并这两个端点的集合edge_count += 1  # 增加已加入的边数return result_val  # 返回最小生成树的权值总和# 主函数，处理输入并输出结果
if __name__ == "__main__":import sysinput = sys.stdin.read  # 读取标准输入data = input().split()v = int(data[0])  # 节点数量e = int(data[1])  # 边的数量edges = []  # 存储所有边index = 2for _ in range(e):v1 = int(data[index])  # 边的左端点v2 = int(data[index + 1])  # 边的右端点val = int(data[index + 2])  # 边的权值edges.append(Edge(v1, v2, val))  # 将边加入到列表中index += 3# 调用 Kruskal 算法求解最小生成树的权值总和result_val = kruskal(v, edges)# 输出最小生成树的总权值print(result_val)

卡码题目链接
题目文章讲解

总结

Prim算法和Kruskal算法都是用于求解 最小生成树（MST） 的经典贪心算法。尽管它们的目标相同，但它们的实现方式和使用的数据结构有所不同。

1. 思路与操作对象的区别
   Prim算法：
   节点为中心：Prim算法从一个起始节点开始，不断向已连接的生成树中添加最小边。它通过逐步扩展树的节点来构建最小生成树。
   局部贪心策略：每次选择的都是与已构建的生成树相连的最小边。
   Kruskal算法：
   边为中心：Kruskal算法从所有边中选择权值最小的边开始，逐步将未连通的部分通过边连接起来。
   全局贪心策略：Kruskal算法直接对所有边进行排序，然后逐步选择不会形成环的最小边。

2. 使用的数据结构
   Prim算法：
   邻接矩阵或邻接表：通常使用邻接矩阵或邻接表来表示图，逐步更新已连接节点与其他未连接节点之间的最小权值。
   优先队列（可选）：使用优先队列（堆）优化查找最小边的操作，复杂度可以优化为 O(E log V)。
   Kruskal算法：
   边列表：Kruskal算法将所有边按权值排序，然后依次选择边，因此直接使用边的列表。
   并查集（Union-Find）：Kruskal算法需要并查集来判断两个节点是否已经在同一集合中，用于检测是否形成环路。

3. 适用的图类型
   Prim算法：
   适用于稠密图：由于 Prim算法逐步扩展已连接的节点集合，因此在边数较多的稠密图中表现较好。
   时间复杂度为 O(V^2)（邻接矩阵）或 O(E log V)（使用优先队列的邻接表）。
   Kruskal算法：
   适用于稀疏图：Kruskal算法对边进行排序并依次选择最小边，在边数较少的稀疏图中表现较好。
   时间复杂度为 O(E log E)，其中 E 是边数。

4. 执行流程
   Prim算法：
   从任意起始节点开始，将该节点标记为已访问。
   每次选择已访问节点集合中与未访问节点集合之间的最小边，将新节点加入最小生成树。
   重复该过程，直到所有节点都被访问。
   Kruskal算法：
   将所有边按权值从小到大排序。
   依次选择最小的边，如果该边连接的两个节点不在同一集合中，则将它们加入最小生成树，并使用并查集进行合并。
   重复该过程，直到树中包含 n-1 条边。

5. 结束条件
   Prim算法：
   当所有节点都已加入生成树时，算法结束。
   Kruskal算法：
   当选中的边数达到 n-1 条时，算法结束（其中 n 是节点数）。