碰撞检测 | 详解圆-矩形碰撞检测与N圆覆盖模型(附ROS C++可视化)
目录
- 0 专栏介绍
- 1 N N N圆覆盖碰撞模型
- 2 圆与矩形的碰撞检测
- 3 算法仿真与可视化
- 3.1 核心算法
- 3.2 仿真实验
0 专栏介绍
🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰撞检测、安全走廊、优化建模(QP、SQP、NMPC、iLQR等)、轨迹优化(梯度法、曲线法等),每个算法都包含代码实现加深理解
🚀详情:运动规划实战进阶:轨迹优化篇
本期实现如下的碰撞检测效果

1 N N N圆覆盖碰撞模型
在车辆的路径规划过程中,需要评估和避开可能的障碍物。 N N N圆覆盖碰撞检测算法可以快速检测和响应路径上的障碍物,从而优化行驶路线。
直观地,如图所示,采用单个外接圆包围物体,此时只需要检查圆心和半径的关系即可实现碰撞检测。然而这种方法容易造成自由空间狭窄,更精细的做法是利用 个圆盘覆盖物体,对这些圆依次进行单圆碰撞检测,如图所示
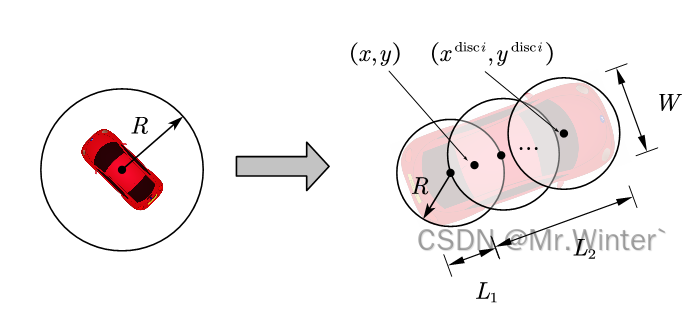
形式化地,设自车后轴中心坐标为 ( x , y ) (x, y) (x,y),由几何关系可知
{ x i d i s c = x + ( 2 i − 1 2 N ⋅ ( L 1 + L 2 ) − L 1 ) cos θ y i d i s c = y + ( 2 i − 1 2 N ⋅ ( L 1 + L 2 ) − L 1 ) sin θ i = 1 , 2 , ⋯ , N \begin{cases} x_{i}^{\mathrm{disc}}=x+\left( \frac{2i-1}{2N}\cdot \left( L_1+L_2 \right) -L_1 \right) \cos \theta\\ y_{i}^{\mathrm{disc}}=y+\left( \frac{2i-1}{2N}\cdot \left( L_1+L_2 \right) -L_1 \right) \sin \theta\\\end{cases}\,\,i=1,2,\cdots ,N {xidisc=x+(2N2i−1⋅(L1+L2)−L1)cosθyidisc=y+(2N2i−1⋅(L1+L2)−L1)sinθi=1,2,⋯,N
其中 θ \theta θ是航向角; N N N是覆盖圆的数量, N N N越大碰撞检测越精细但同时计算负担更大。圆的半径由 N N N和自车几何形状唯一确定
R d i s c = ( L 1 + L 2 2 N ) 2 + ( W 2 ) 2 R^{\mathrm{disc}}=\sqrt{\left( \frac{L_1+L_2}{2N} \right) ^2+\left( \frac{W}{2} \right) ^2} Rdisc=(2NL1+L2)2+(2W)2
2 圆与矩形的碰撞检测
如图所示,核心原理是计算圆心与矩形的最短距离 ∣ u ∣ \left| \boldsymbol{u} \right| ∣u∣,若 ∣ u ∣ < r \left| \boldsymbol{u} \right|<r ∣u∣<r则两者相交。算法上,首先考虑无旋转的矩形,不失一般性地将圆投影到第一象限,得到
v = [ ∣ p x − c x ∣ ∣ p y − c y ∣ ] T \boldsymbol{v}=\left[ \begin{matrix} \left| p_x-c_x \right|& \left| p_y-c_y \right|\\\end{matrix} \right] ^T v=[∣px−cx∣∣py−cy∣]T
其中 p \boldsymbol{p} p与 c \boldsymbol{c} c分别是矩形和圆的中心向量。设 l − l^- l−、 w − w^- w−分别为矩形长、宽的一半,则矩形中心到第一象限顶点向量为 h = [ l − w − ] \boldsymbol{h}=\left[ \begin{matrix} l^-& w^-\\\end{matrix} \right] h=[l−w−],从而得到最近距离向量
u = [ max ( v x − h x , 0 ) max ( v y − h y , 0 ) ] T \boldsymbol{u}=\left[ \begin{matrix} \max \left( v_x-h_x, 0 \right)& \max \left( v_y-h_y, 0 \right)\\\end{matrix} \right] ^T u=[max(vx−hx,0)max(vy−hy,0)]T
即将负数分量设为0;再比较 ∣ u ∣ \left| \boldsymbol{u} \right| ∣u∣和圆的半径大小关系即可
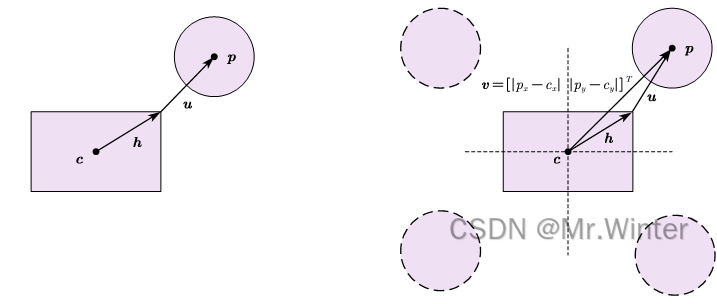
推广到一般情形,设矩形旋转角度为 α \alpha α,则只需要将 v \boldsymbol{v} v反向旋转 α \alpha α角度即可转换为无旋转的场景,算法流程如下所示

3 算法仿真与可视化
3.1 核心算法
核心算法如下所示
-
圆与矩形的碰撞检测
auto other_rect = std::dynamic_pointer_cast<VRectangle>(other);for (const auto& disc : discs_) {auto v = disc.first - other_rect->center();// rotate ang project first quadrantfloat theta = -other_rect->angle();float rotate_vx = std::fabs(v.x * std::cos(theta) - v.y * std::sin(theta));float rotate_vy = std::fabs(v.x * std::sin(theta) + v.y * std::cos(theta));// right-top point of rectanglefloat h_x = std::fabs(other_rect->length()) / 2.0f;float h_y = std::fabs(other_rect->width()) / 2.0f;// closest vectorfloat u_x = std::max(0.0f, rotate_vx - h_x);float u_y = std::max(0.0f, rotate_vy - h_y);if (std::hypot(u_x, u_y) < disc.second)return true; } return false; -
圆与圆的碰撞检测
auto other_circle = std::dynamic_pointer_cast<VCircle>(other); const auto& other_circle_center = other_circle->center(); const auto& other_circle_radius = other_circle->radius();for (const auto& disc : discs_) {if (std::hypot(other_circle_center.x - disc.first.x, other_circle_center.y - disc.first.y) <=disc.second + other_circle_radius)return true; } return false;
3.2 仿真实验
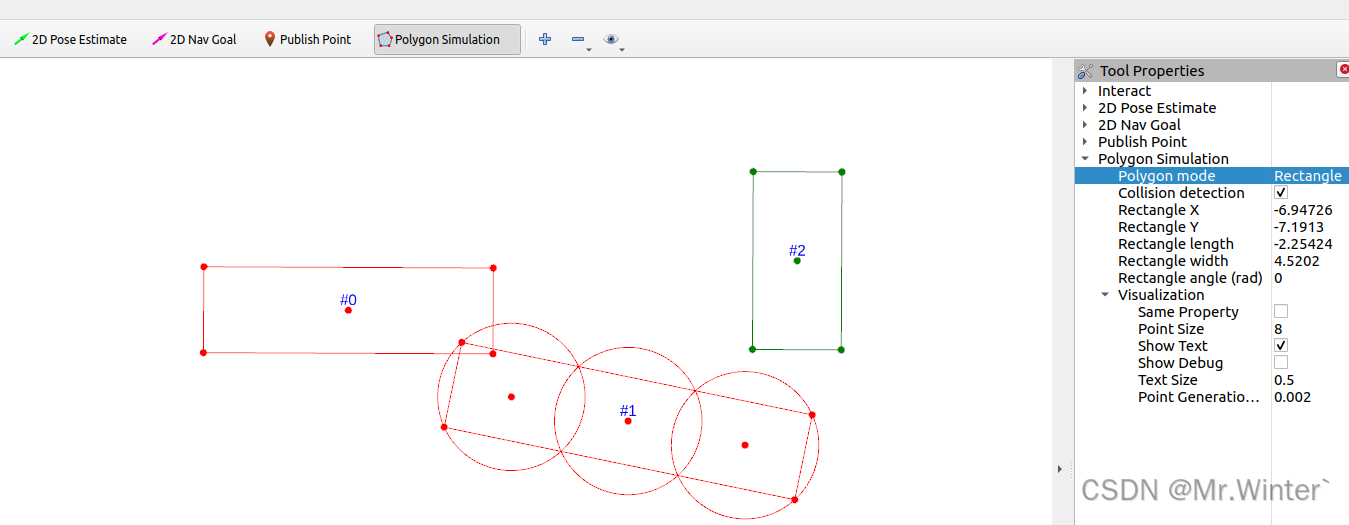
通过Rviz->Add New Tool添加Polygon Simulation插件

开启碰撞检测功能后,验证 N N N圆覆盖碰撞检测算法
- 单圆碰撞与无碰撞情形
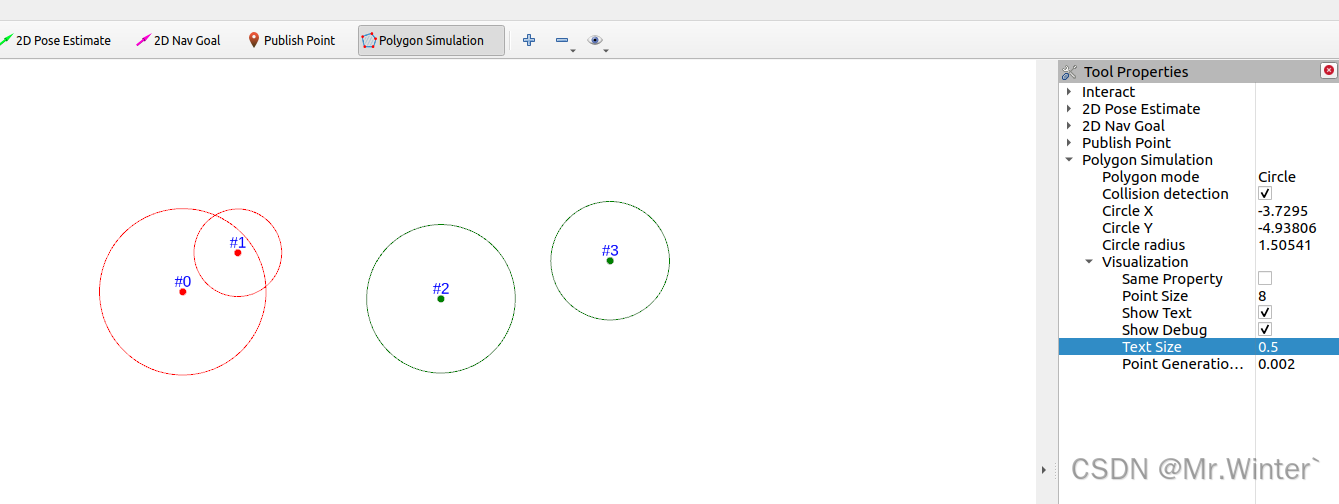
- N N N圆覆盖模型与圆的碰撞检测
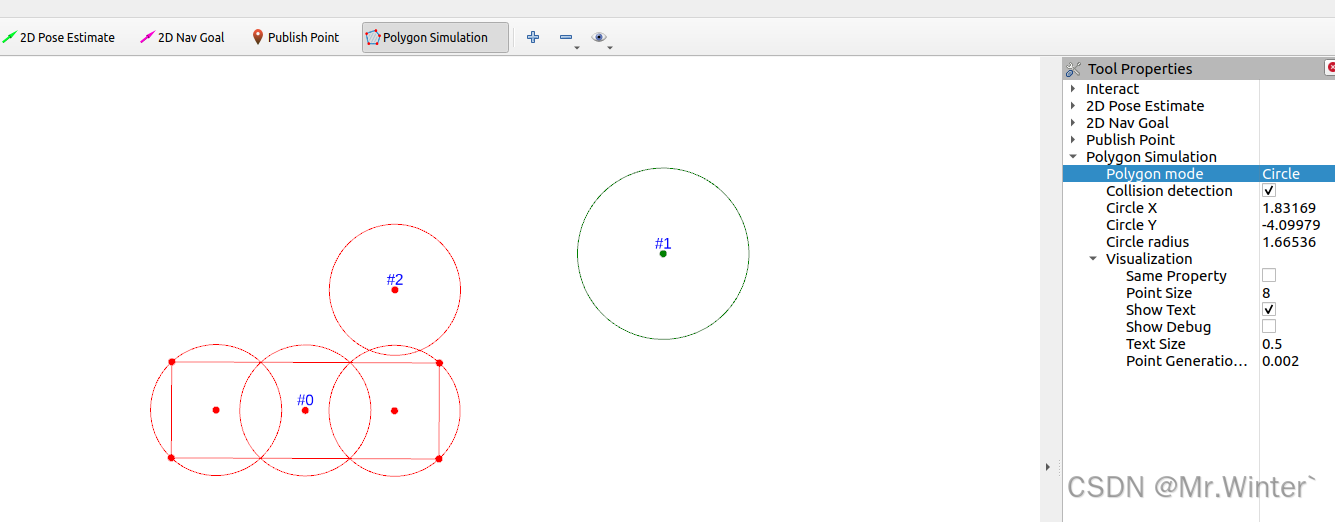
- N N N圆覆盖模型与矩形的碰撞检测
完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

碰撞检测 | 详解圆-矩形碰撞检测与N圆覆盖模型(附ROS C++可视化)
目录 0 专栏介绍1 N N N圆覆盖碰撞模型2 圆与矩形的碰撞检测3 算法仿真与可视化3.1 核心算法3.2 仿真实验 0 专栏介绍 🔥课设、毕设、创新竞赛必备!🔥本专栏涉及更高阶的运动规划算法轨迹优化实战,包括:曲线生成、碰…...

pandas读取Excel文件单元格中的百分数时保持数据格式及精度
pandas读取Excel文件单元格中的百分数时保持数据格式及精度 在使用Pandas读取Excel文件时,通常Excel中的百分数会被转换为浮点数。在这种情况下,如果你希望保留数据的格式和精度,有几个步骤可以帮助你实现这个目标: 读取数据:使用Pandas的read_excel函数来读取Excel文件。…...

【重学 MySQL】二十五、等值连接vs非等值连接、自连接vs非自连接
【重学 MySQL】二十五、等值连接vs非等值连接、自连接vs非自连接 等值连接(Equijoin) vs 非等值连接(Non-equijoin)等值连接(Equijoin)非等值连接(Non-equijoin) 自连接(…...

Springboot工程配置https访问
背景 因为前端工程使用nginx配置了https访问,在https直接请求我们Springboot后端的http接口会报错。那么我们就需要配置使得我们后端的springboot服务支持https访问。 证书生成 在配置springboot工程https之前,我们需要生成自签名证书以及Spring Boot…...

智慧水务建设的核心内容
智慧水务解决方案的主要对象客户是全国各地水务投资集团、水务局、水司、水厂、农水办,也会有少量项目涉及到住建局或城管局。解决方案通常会以具体的某个业务单位的职能工作为切入点,配合物联感知、大数据分析、人工智能等技术手段,为城市供水、乡村供水的水质安全、供水调…...

opencv之图像轮廓
文章目录 前言查找并绘制轮廓查找图像轮廓:findContours函数绘制图像轮廓:drawContours函数轮廓实例 矩特征Hu矩Hu矩函数形状匹配 前言 图像轮廓指的是图像中物体边缘或形状的外部线条,通常通过图像处理技术来检测和提取。轮廓是用于描述物体…...

shader 案例学习笔记之step函数
step函数 参数是float step(edge,x):当x>edge时返回1,否则返回0 #ifdef GL_ES precision mediump float; #endifuniform vec2 u_resolution;void main(){vec2 st gl_FragCoord.xy/u_resolution.xy;float f step(0.5, st.x);gl_FragColor vec4(f…...

node快速复制文件或文件夹,排除部分文件(node_modules)
const fs require(fs) const path require(path)/*** description: 获取完整的文件路径* param {*} url 路径* return {*} 返回完整的文件路径*/ const getPath (url) > {return path.join(__dirname, url) }/*** description: 获取参数* return {*} target【目标文件夹】…...

网络层 VIII(网络层设备——路由器)【★★★★★★】
一、冲突域与广播域 这里的“域”表示冲突或广播在其中发生并传播的区域。 1. 冲突域 冲突域是指连接到同一物理介质上的所有结点的集合,这些结点之间存在介质争用的现象(能产生冲突的所有设备的集合)。也就是说,若这些设备同时发…...

302.AI学术论文搜索工具的智能体验
Hey朋友们, 你是否曾在学术的海洋里迷失方向,为了找到一篇论文而苦苦挣扎? 就像在茫茫大海中寻找灯塔,我们渴望一盏明灯,指引我们前行。 别担心,今天我来给你介绍一个超级给力的工具——302.AI学术论文…...

arm平台常用工具和动态库编译
目录 perf 交叉编译交叉编译zlib交叉编译 elfutils交叉编译 perfperf 使用 libconfig 交叉编译openssl 交叉编译libpcap 交叉编译统信、龙芯等平台编译QT交叉编译编译QT源码编译QtCreator 编译ssl编译libsrtp(2.3.0版本)编译libyuvlibopus编译libopenh264编译libusrsctp编译lib…...

代码随想录训练营day45|115.不同的子序列,583. 两个字符串的删除操作,72. 编辑距离
115.不同的子序列 题目 dp[i][j]表示的是在以是s[j]为结尾的字符串中最多可以找到几种组成以t[i]为结尾的字符串的方式。 如果s[i]t[j], 1.利用第i个和第j个匹配,在j-1中寻找i-1. 2.不适用这两个进行匹配,在j-1中寻找i 如果s[i]!…...

椋鸟C++笔记#7:标准模板库STL初识
文章目录 标准模板库(Standard Template Library)STL的版本P.J.版RW版SGI版 STL的组成部分 萌新的学习笔记,写错了恳请斧正。 标准模板库(Standard Template Library) 标准模板库STL,是C标准库的一个非常重…...

滴滴嘀嗒,出行行业响起Robotaxi“倒计时”
文:互联网江湖 作者:刘致呈 前几天,各大出行平台的半年报陆续披露完毕,有的还在亏损,但也有人开始盈利。 如祺出行上市后的首份半年报营收10.37亿,同比增长13.6%。上半年运营亏损为2.56亿元,同…...

【MATLAB源码-第264期】基于matlab的跳频通信系统仿真,采用MSK调制方式,差分解调;输出误码率曲线和各节点波形图。
操作环境: MATLAB 2022a 1、算法描述 跳频通信系统是一种能够提高通信抗干扰能力的技术,它通过在传输过程中不断地改变载波频率来避开干扰或者窃听。在这套跳频通信系统中,我们采用了最小频移键控(MSK)作为调制方式…...

如何在多台电脑上同步 VSCode配置和插件
上一篇文章最新前端开发VSCode高效实用插件推荐清单总结了前端开发实用的插件,换电脑的时候怎么同步这些配置与插件呢,难道又要重新安装一遍吗😱 现在就来聊聊要在多台电脑上同步 VSCode配置和插件的几种方法: 方法一࿱…...

深度优先算法,广度优先算法,hill climbing,贪心搜索,A*算法,启发式搜索算法是什么,比起一般搜索法算法有什么区别
深度优先算法(Depth-First Search, DFS) 深度优先搜索是一种用于遍历或搜索树或图的算法。它沿着树的深度遍历树的节点,尽可能深地搜索树的分支。当节点v的所在边都已被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程…...

《python语言程序设计》2018版第8章第14题金融:信用卡号合法性 利用6.29题
一、之前6.29题我做的代码 这是用数字来进行分辨的 is_txt 4383576018402626 #合法def split_the_data_even(vis_n):current_a1 vis_n // 10000a_t1 vis_n % 10000# print("1th", a_t1)a_t2 current_a1 % 10000# print("2th", a_t2)current_a3 curre…...

QT 基础学习
1> 使用绘制事件完成钟表的绘制 头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPainter> #include <QDebug> #include <QTime> #include <QTimer> #include <QDateTime> //#include <string> #includ…...

【Gephi】可视化教程
此教程专供欣欣向荣及其舍友使用 文章目录 导入数据上色改变布局设置节点大小统计拓扑结构输出图形保存文件 导入数据 点击【文件】-【导入电子表格】 先选择csv格式的network 直接下一步 点击完成 【图的类型】改为“有向的” 点击确认 会弹出报错,直接clos…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
