高阶数据结构之 B树 B+树 B*树
文章目录
- B树
- B树节点的设计
- 插入key的过程
- B树的验证
- B树的性能分析
- B+树和B*树
- B+树
- B*树
- 总结B树、B+树、B*树
- B树的应用
- 做索引
- MySQL索引
- MyISAM
- InnoDB
B树
在前面几章中我们介绍了AVL树和红黑树,简单复习一下,我们说到原本的二叉搜索树会存在缺陷(不能保证树的平衡,可能会退化成一个链表),由此引入了AVL树和红黑树来限制树的高度,以提高搜索的效率。
但是,不管是以上的哪种树,在对树进行元素查找的时候,都是需要先将数据加载到内存中再进行查找的,而如果数据量太大,以至于内存已经存储不下了,那么再使用上面的这些数据结构就都不成立了。
为了解决这个问题,就引出了一种适合外查找(也就是不需要依赖内存,一般来说外部查找是在磁盘或其他外部存储设备上进行的)的树,它是一种平衡的多叉树,称为B树。
其中,一颗M阶的B树,是一颗平衡的M路平衡搜索树,可以是空树或者是满足以下的性质:
(1)根节点至少有两个孩子。
(2)每个非根节点至少有M/2-1(上取整)个关键字,至多有M-1个关键字,并且以升序排序。
(3)每个非根节点至少有M/2(上取整)个孩子,至多有M个孩子。
(4)key[i]和key[i+1]之间的孩子节点的值是介于key[i]和key[i+1]之间的。
(5)所有叶子节点都在同一层上。
以上是B树的性质,在操作B树无论什么时候都要遵循这些性质,下面以一个简单的例子看一下B树插入的流程:
第一阶段:
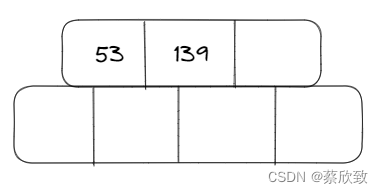
当插入一个元素值为75的时候:

第二阶段:
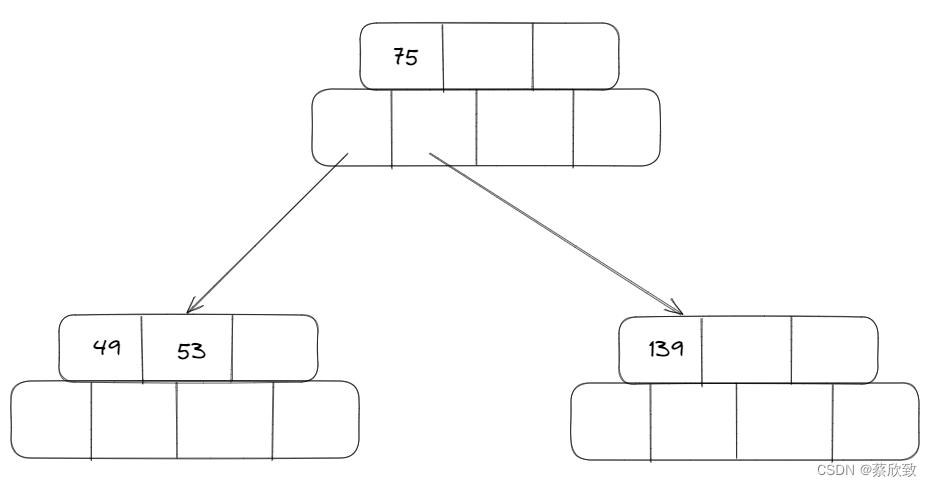
当插入一个元素值为36的时候:
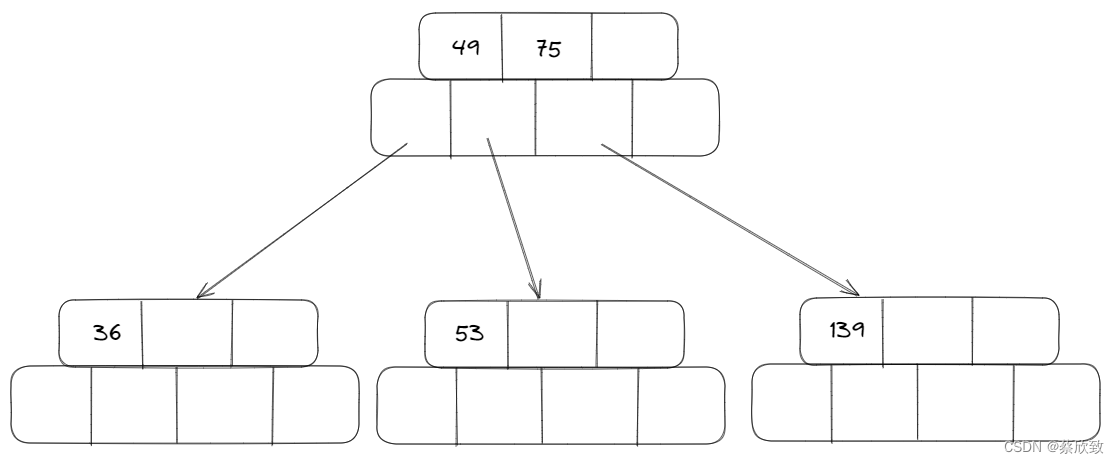
第三阶段:
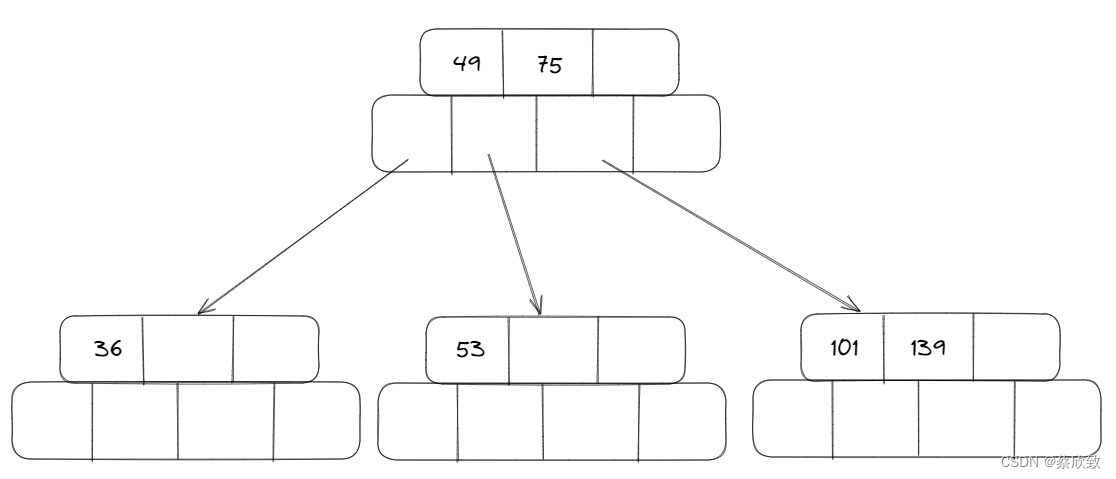
当插入一个元素值为145的时候:
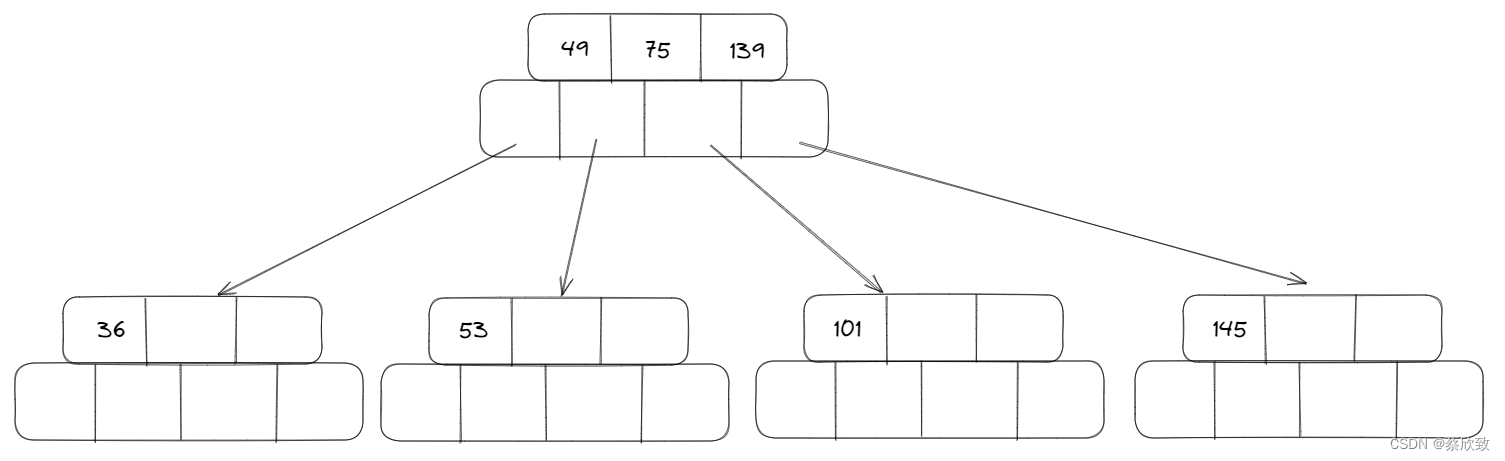
首先会变成这样,但是不满足B树的性质,所以还需要继续调整:
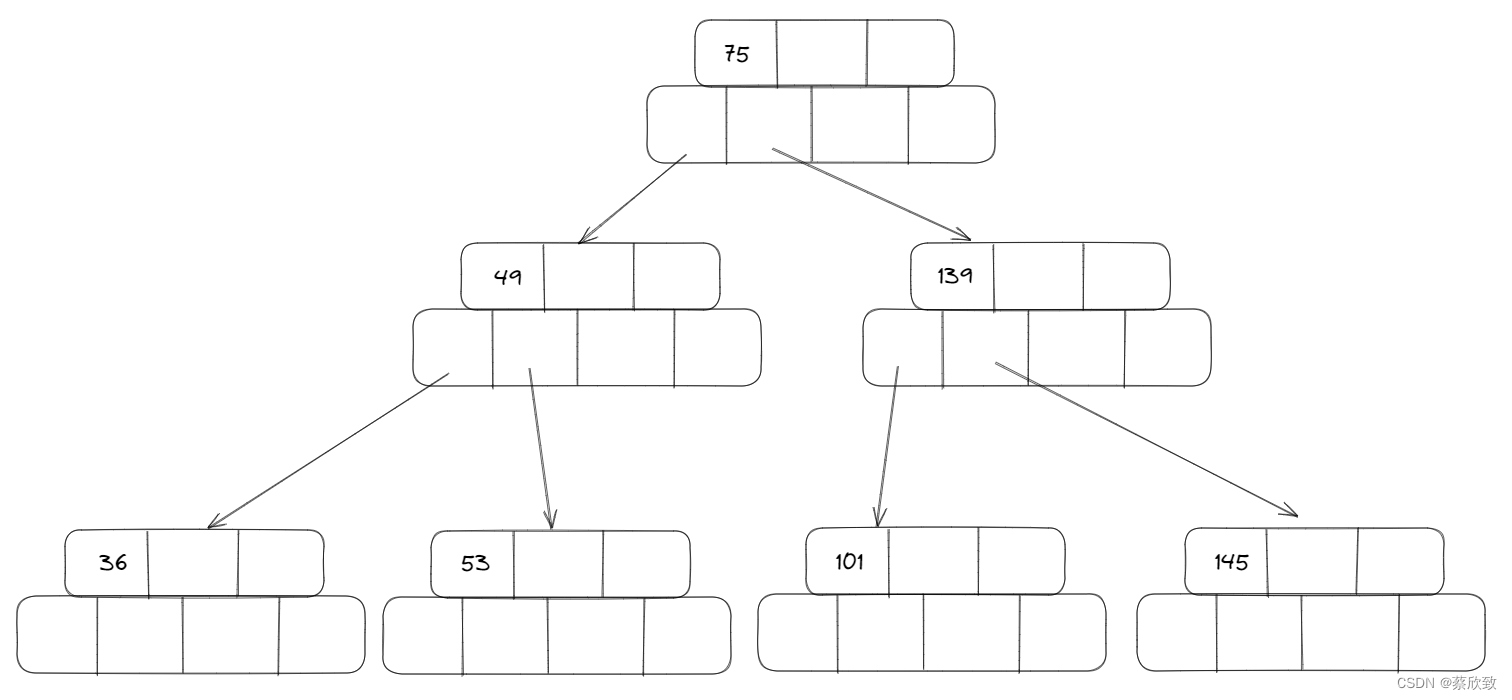
总结:
1. 如果树为空的话,直接插入新节点中,该节点为树的根节点。
2. 树非空的时候,找待插入元素在树中的插入位置(找到的插入节点位置一定要在叶节点中)。
3. 检测是否找到插入位置(假设树中的key唯一,即这个元素已经存在,不允许再插入)。
4. 按照插入排序的思想将该元素插入到找到的节点中。
5. 检测节点是否满足B树的性质(即该节点中的元素个数是否等于M,如果小于则满足)。
6. 如果插入后节点不满足B树的性质,则需要对该节点进行分裂(申请新节点、找到该节点的中间位置、将该节点中间位置右侧的元素以及其孩子搬移到新节点中、将中间位置元素以及新节点往该节点的双亲节点中插入)。
7. 如果向上已经分裂到根节点的位置,则插入结束。
B树节点的设计
static class BTreeNode{public int[] keys; //关键字public BTreeNode[] subs; //孩子public BTreeNode parent; //父节点public int usedSize; //关键字数量public BTreeNode(){this.keys = new int[M];this.subs = new BTreeNode[M + 1];}}
插入key的过程
//插入操作public boolean insert(int key){if(root == null){root = new BTreeNode();root.keys[0] = key;root.usedSize++;return true;}//首先查看当前树中是否存在key节点Pair<BTreeNode, Integer> pair = find(key);if(pair.value != -1){return false;}BTreeNode parent = pair.key;int index = parent.usedSize - 1;for(; index >= 0; index--){if(parent.keys[index] >= key){parent.keys[index + 1] = parent.keys[index];}else{break;}}parent.keys[index + 1] = key;parent.usedSize++;if(parent.usedSize >= M){split(parent);return true;}else{return true;}}//分裂当前节点private void split(BTreeNode cur) {BTreeNode newNode = new BTreeNode();BTreeNode parent = cur.parent;int mid = cur.usedSize >> 1;int i = mid + 1;int j = 0;for(; i < cur.usedSize; i++, j++){newNode.keys[j] = cur.keys[i];newNode.subs[j] = cur.subs[i];//记得更新父节点if(newNode.subs[j] != null){newNode.subs[j].parent = newNode;}}newNode.subs[j] = cur.subs[i]; //记得多拷贝一次//记得更新父节点if(newNode.subs[j] != null){newNode.subs[j].parent = newNode;}//更新新节点的参数newNode.parent = parent;newNode.usedSize = j;cur.usedSize = cur.usedSize - j - 1;//特殊处理根节点的情况if(cur == root){root = new BTreeNode();root.keys[0] = cur.keys[mid];root.subs[0] = cur;root.subs[1] = newNode;root.usedSize = 1;cur.parent = root;newNode.parent = root;return;}int endT = parent.usedSize - 1;int midVal = cur.keys[mid];for(; endT >= 0; endT--){if(parent.keys[endT] >= midVal){parent.keys[endT + 1] = parent.keys[endT];parent.subs[endT + 2] = parent.subs[endT + 1];}else{break;}}parent.keys[endT + 1] = midVal;parent.subs[endT + 2] = newNode;parent.usedSize++;if(parent.usedSize >= M){split(parent);}}//查找元素是否在树中存在private Pair<BTreeNode, Integer> find(int key) {BTreeNode cur = root;BTreeNode parent = null;while(cur != null){int i = 0;while(i < cur.usedSize){if(cur.keys[i] == key){return new Pair<>(cur, i);}else if(cur.keys[i] < key){i++;}else{break;}}parent = cur;cur = cur.subs[i];}return new Pair<>(parent, -1);}
B树的验证
对B树的验证其实就是对B树进行中序遍历,如果此时能得到一个有序的序列,那么则可以说明B树的插入是正确的。
private void inorder(BTreeNode root){if(root == null)return;for(int i = 0; i < root.usedSize; ++i){inorder(root.subs[i]);System.out.println(root.keys[i]);}inorder(root.subs[root.usedSize]);}
B树的性能分析
对于一棵节点为N度为M的B树来说,树的高度会在log(M-1)N和log(M/2)N之间,采用二分查找的方式可以快速定位到该元素,大大减少了读取磁盘的次数。
B+树和B*树
B+树
B+树也是一种多路搜索树,是B树的一种变形,他的定义基本和B树是相同的。
不同点:
1. 非叶子节点的子树指针与关键字个数相同。
2. 非叶子节点的子树指针p[i],指向关键字值属于(k[i], k[i+1])的子树。
为所有叶子节点增加一个链指针。
5. 所有关键字都在叶子节点出现。
以下是B+树的基本示意图(辅助理解):
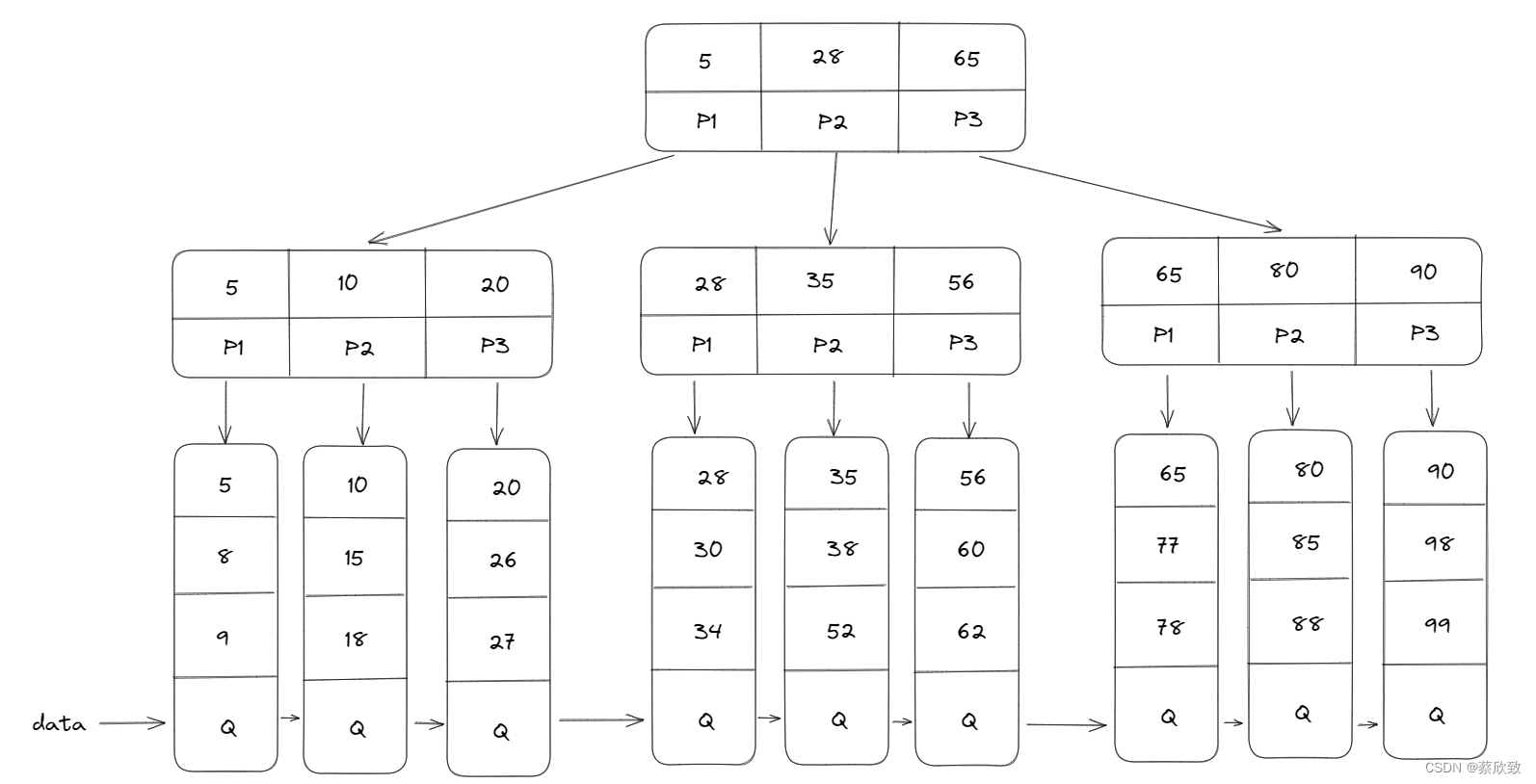
总结: B+树的搜索基本上和B树是相同的,区别是B+树只有达到叶子节点才能命中(B树可以在非叶子节点中命中),此处的命中指的是查询插入操作,他的性能也是等价于在关键字全集做一个二分查找。所有关键字都出现在叶子节点的链表中(稠密索引),且链表中的节点都是有序的;非叶子节点相当于是叶子节点的稀疏索引(不可能会在非叶子节点中命中),叶子节点相当于是存储数据的数据层;综上所述:B+树整体上来说,会更适合做文件索引的系统。
B*树
B*树又是B+树的变形,在B+树的非根和非叶子节点再增加指向兄弟节点的指针。
以下是B树的基本示意图(辅助理解):
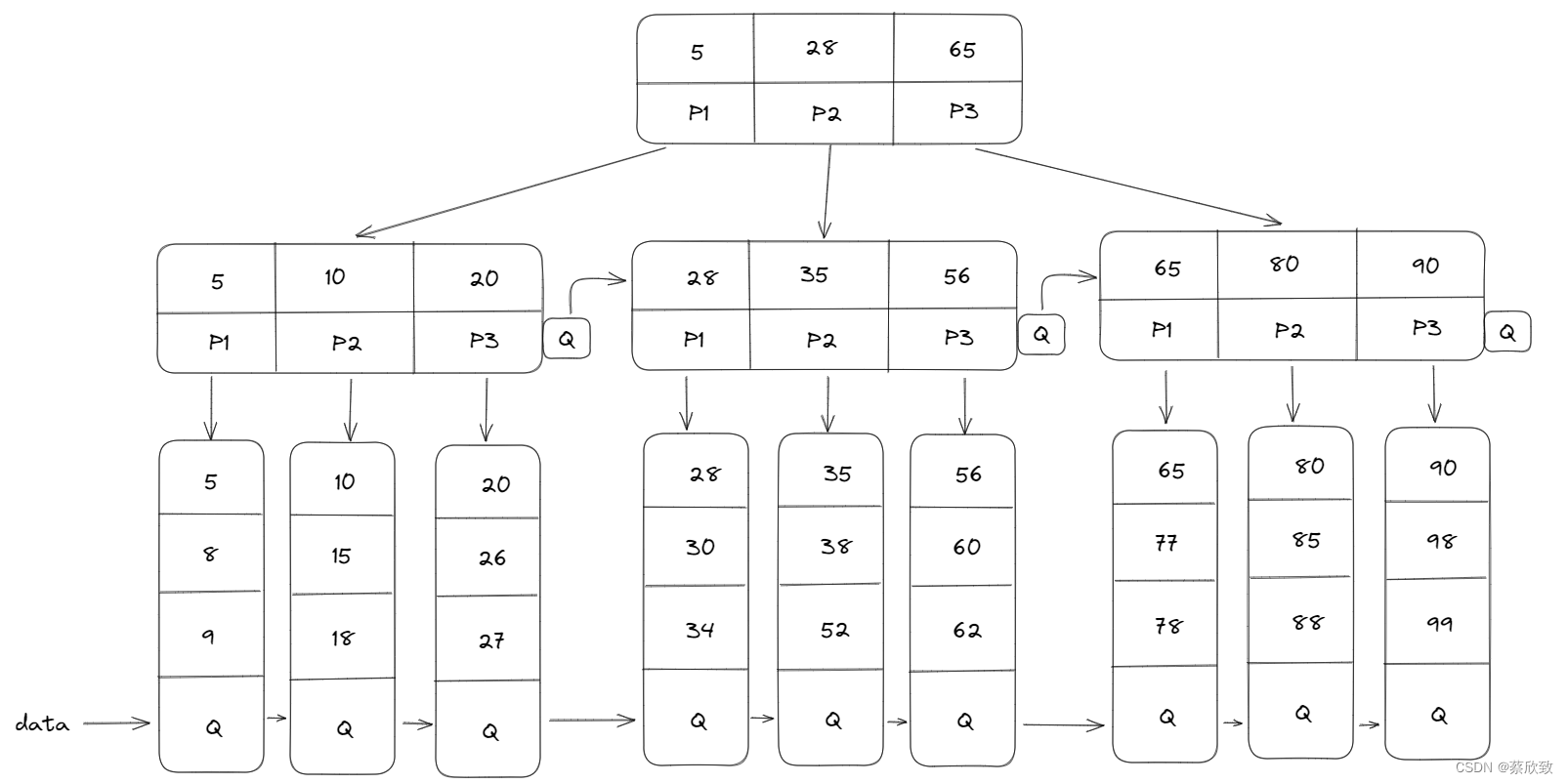
总结: B树在分裂的时候,当一个节点满的时候,如果它的下一个兄弟节点未满,那么将一部分数据移到兄弟节点中,再在原节点插入关键字,最后修改父节点中的兄弟节点的关键字,最后修改父节点中兄弟节点的关键字(因为兄弟节点的关键字范围被改变了);如果兄弟也满了,则会在原节点与兄弟节点之间增加新节点,并各复制1/3的数据到新节点,最后在父节点增加新节点的指针。所以,B*树分配新节点的概率比B+树要低,空间的使用率更高。
总结B树、B+树、B*树
B树:多路搜索树,每个节点存储M/2到M个关键字,非叶子节点存储指向关键字范围的子节点,所有关键字在整棵树中只会出现一次,非叶子节点可以命中。
B+树:在B树的基础上,为叶子节点增加链表指针,所有关键字都在叶子节点中出现,非叶子节点仅作为叶子节点的索引,只有到叶子节点才会被命中。
B*树:在B+树的基础上,为非叶子节点也增加了链表指针,将节点的最低利用率从1/2提高到2/3。
B树的应用
做索引
B树最常见的应用就是用来做索引。索引通俗来说就是为了方便用户快速找到目标的东西,例如我们的搜索网站,本质上就是互联网页面中的索引结构,有了这个索引就可以快速找到有价值的分类网站(这让我想到之前做的搜索引擎项目中倒排索引的构建,是比较相似的)。
索引在MySQL数据库中也有被应用,MySQL官方对索引的定义:索引是帮助MySQL高效获取的数据结构,当数据量很大的时候,为了能够方便管理数据,提高数据查询的效率,一般都会选择将数据保存到数据库中,因此数据库不仅仅是帮助用户管理数据,而且还维护着满足特定查找算法的数据结构,这些数据结构以某种方式引用数据,这样就可以在这些数据结构上实现高级查找算法,这个数据结构就是索引。
MySQL索引
对于MySQL底层使用的数据结构,我之前有写过一篇相关文章,地址:https://blog.csdn.net/Faith_cxz/article/details/125871321?spm=1001.2014.3001.5501,可以当做部分参考~
MyISAM
MyISAM引擎是MySQL5.5.8版本之前默认的存储引擎,不支持事务,支持全文检索,使用B+树作为索引结构,叶节点的data域存放的是数据记录的地址。
MyISAM中索引检索的算法为首先按照B+树搜索算法搜索索引,如果指定的key存在,则取出其data域的值,然后以data域的值为地址,读取相应的数据记录,MyISAM的索引方式也叫做“非聚簇索引”。(关于聚簇索引和非聚簇索引的相关知识点可以先简单看一下这篇文章:一分钟明白MySQL聚簇索引和非聚簇索引)
InnoDB
InnoDB存储引擎支持事务,其设计目标主要面向在线事务处理的应用,从MySQL5.5.8版本开始,InnoDB存储引擎就是默认的存储引擎。InnoDB支持B+树索引、全文索引、哈希索引,但是InnoDB使用B+树作为索引结构是,具体的实现方式与MyISAM是不一样的。
区别一: MyISAM索引文件和数据文件是分离的,索引文件仅保存数据记录的地址;而InnoDB的表数据文件本身就是按B+树组织的索引结构,这棵树的叶节点data域保存了完整的数据记录,这个索引的key是数据表的主键,因此InnoDB表数据文件本身就是主索引。
区别二: InnoDB的辅助索引data域存储相应记录主键的值而不是地址,所有辅助索引都引用主键作为data域。聚簇索引的这种实现方式使得按主键的搜索十分高效,但是辅助索引需要检索两遍索引:首先检索辅助索引获得主键,然后用主键到主索引中检索获得记录。
注意:索引是基于表的,不是基于数据库的。
由于本文总结的是B树和B+树相关的知识点,所以MySQL的底层简略带过,后面我会查阅更多文章,总结出MySQL详细的知识点~
相关文章:

高阶数据结构之 B树 B+树 B*树
文章目录B树B树节点的设计插入key的过程B树的验证B树的性能分析B树和B*树B树B*树总结B树、B树、B*树B树的应用做索引MySQL索引MyISAMInnoDBB树 在前面几章中我们介绍了AVL树和红黑树,简单复习一下,我们说到原本的二叉搜索树会存在缺陷(不能保…...

CSS3之动画属性
系列文章目录 前端系列文章——传送门 CSS系列文章——传送门 文章目录系列文章目录CSS3 中的动画第一步:定义一个动画第二步:执行这个动画第三步:暂停或启动这个动画过渡和动画的区别CSS3 中的动画 CSS3 动画是使元素从一种样式逐渐变化为…...
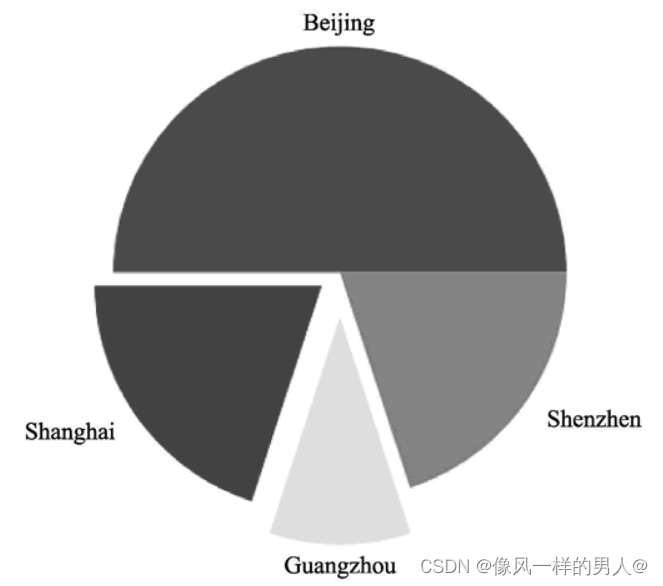
python --Matplotlib详解
安装 pip install matplotlib导包 import matplotlib.pyplot as plt绘制散点图 如果输入的是两个列表,一个表示 x 轴的值,一个表示 y 轴的值,那么就可以在直角坐标系中划出很多个点,然后将这些点用指定的线段连接起来就得到了散…...
手机(Android)刷NetHunter安装指南,无需ssh执行kali命令, NetHunter支持的无线网卡列表!
一、安装NetHunter 前提:确保手机已经root,已装上magisk。如果没有root,可用尝试magisk root 后执行此文 1、下载Nethunter:Get Kali | Kali Linux 然后push 到sdcard 里, 2、打开magisk,选择刚刚下好的…...

教育行业ChatGPT的新挑战
随着科技不断发展,AI的水平越来越高,尤其是最近火出圈的ChatGPT不仅仅可以与人类对话,而且还可以为人们提供关于各种信息帮助。 作为一个先进的“聊天”AI,无论是正苦恼,还是只是需要一些关于如何更有效地管理时间的建…...
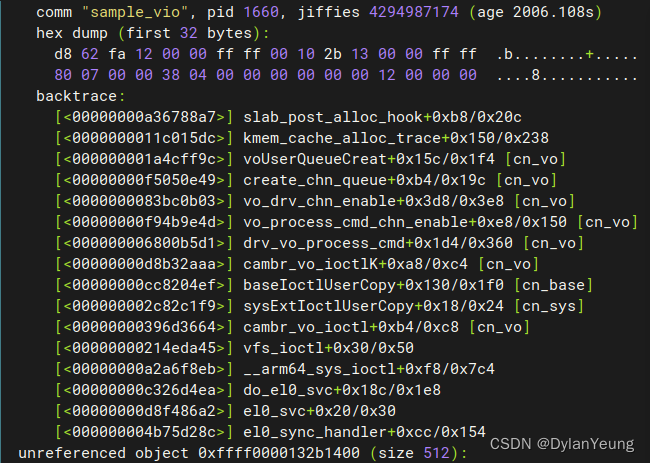
内存泄漏 定位方法
目录 内存概念 物理内存 虚拟内存 内存泄漏 定位方法和手段 1.MemInFo MemTotal MemFree MemAvailable Cached 2 vmalloc info 3.Kmemleak 算法原理 使用方法 参考文献与链接: 如果你点进这篇文章,那么要么你是一个C\C程序员,…...
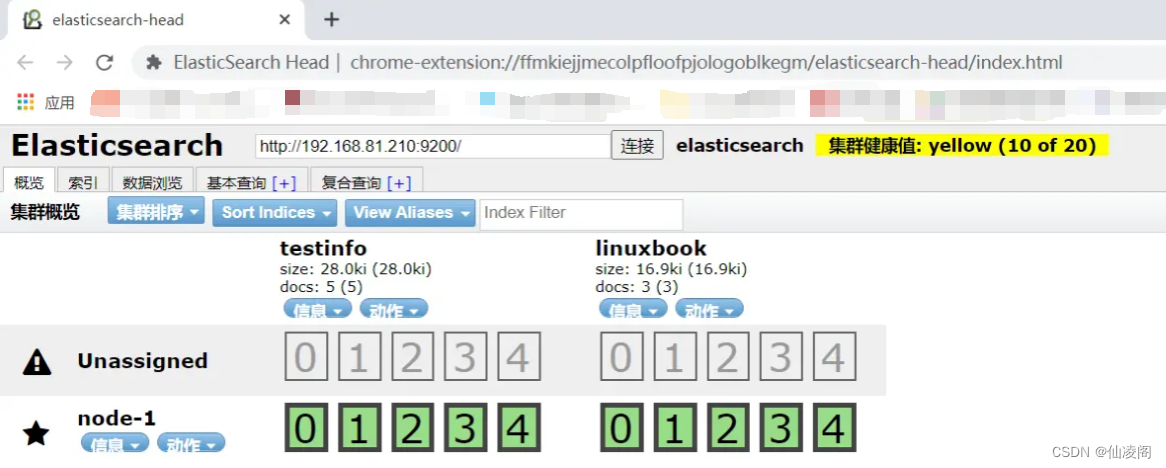
es-head插件插入查询以及条件查询(五)
es-head插件插入查询以及条件查询 1.es-head插件页面介绍 页面详细介绍 2.es-head查询语句 2.1.查询索引中的全部数据 curl命令交互,采用GET请求 语法格式: curl -XGET es地址:9200/索引名/_search?pretty [rootelaticsearch ~]# curl -XGET 192…...
安装python教程并解决Python安装完没有Scripts文件夹问题
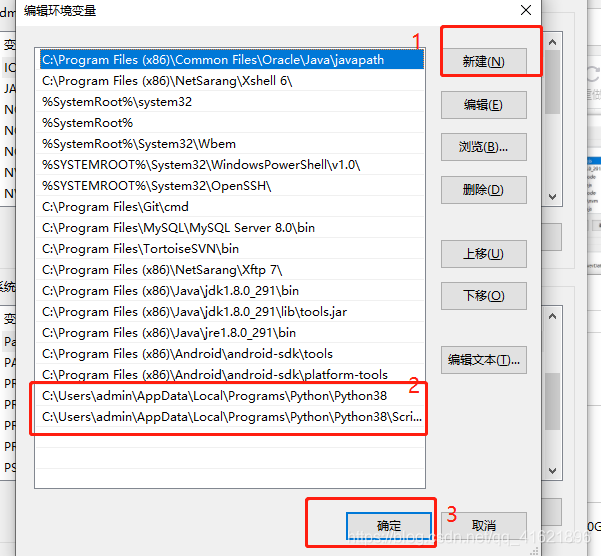
安装python教程 并解决Python安装完没有Scripts文件夹问题 ** 一背景 **首先要了解这个出现的原因是下载安装的版本问题 系統是32 bit 的版本还是 64bit 的 web-based: 透过网络安装的,就是执行安装后才透过网络下载python executable: 可執行文件的ÿ…...
postman的断言、关联、参数化、使用newman生成测试报告
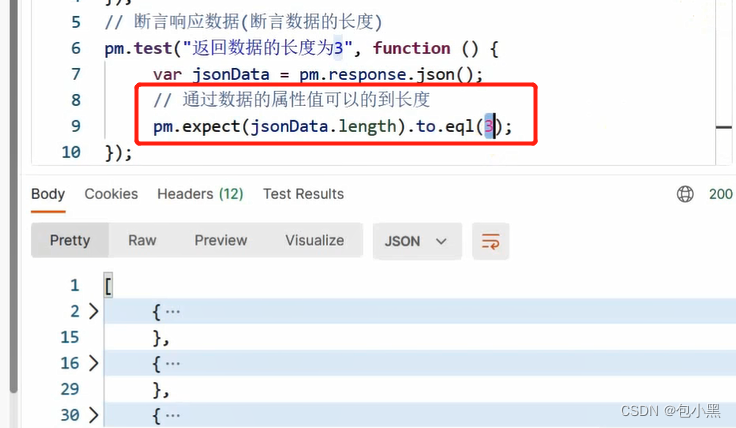
Potman 断言 Postman 断言简介 让 Postman工具 代替 人工 自动判断 预期结果 和 实际结果 是否一致断言代码 书写在 Tests 标签页中。 查看断言结果 Test Results 标签页 Postman 常用断言 1. 断言响应状态码 Status code:Code is 200 // 断言响应状态码为 200…...

春招大盘点:找工作除了招聘网站还有哪些渠道?
又是一年毕业季,估计同学们都正在写论文、找工作两头忙,很多同学和小C“诉苦”说现在找实习的渠道太少了,招聘网站都刷完了,也没看到很合适的岗位。那找工作除了招聘网站还有什么渠道呢?其实是有的,今天就为…...
eNSP 构建基本WLAN
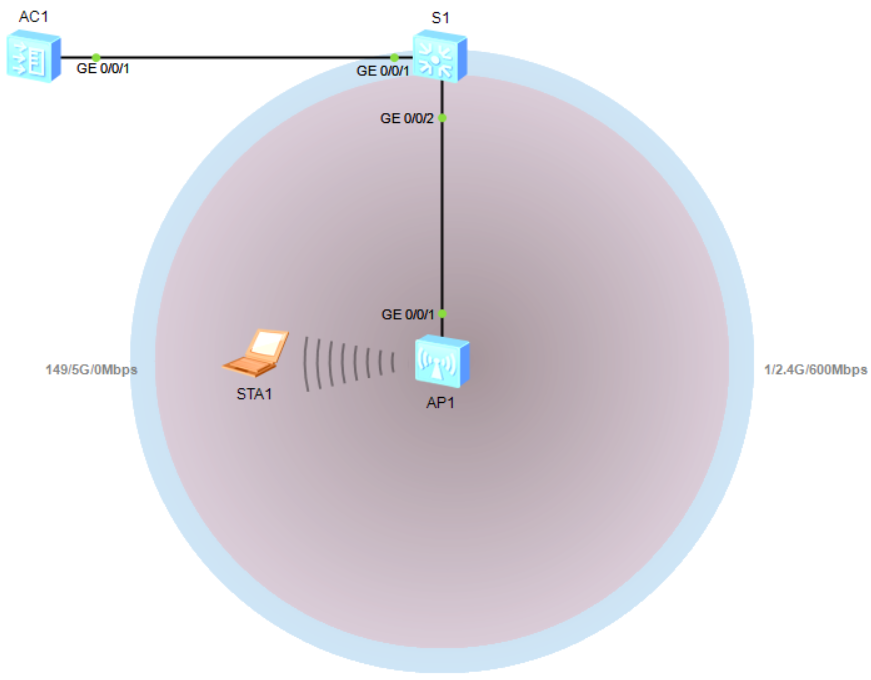
配置项配置参数AP组 名称:hcia-group 应用模板:域管理模板hcia-domain、VAP模板hcia-vap 域管理模板 名称:hcia-domain 国家码:cn SSID模板 名称:hcia-ssid SSID名称:hcia-wlan 安全模板 名称:h…...

Python是不是被严重高估了?
Python起源一种shell的脚本语言 ,而现在已经发展成最通用的语言之一了,TIOBE指数的数据显示,Python是目前世界上最受欢迎的编程语言。 Python之所以这么受欢迎有很多原因。从Web开发到物联网编程再到AI等各个方面都能用到它。另外Python代码…...

给你一个购物车模块,你会如何设计测试用例?【测试用例设计】
测试购物车 从使用场景上,把自己想象成一个使用购物车的人,模拟流程,可以主要从两个方面进行考虑: 涉及操作:增(添加商品)删(删除商品)改(编辑、跳转商品&a…...
【wps】【毕业论文】三线表的绘制
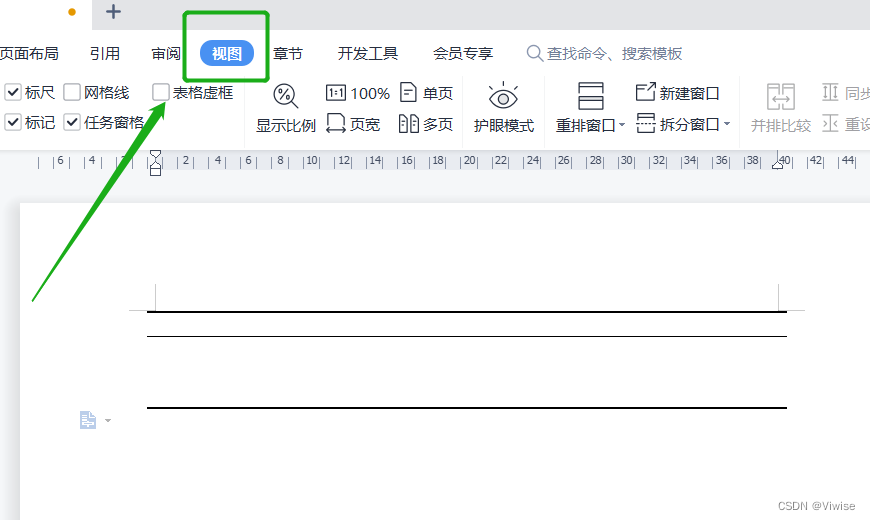
目录 一、三线表 二、制作步骤 (1)点击“插入”——点击“表格”创建一个表格 (2)选中整个表格——鼠标右键选择“边框和底纹”,“表格属性”再点击“边框和底纹”——点击“自定义”——选择表格的边的宽度——如图…...
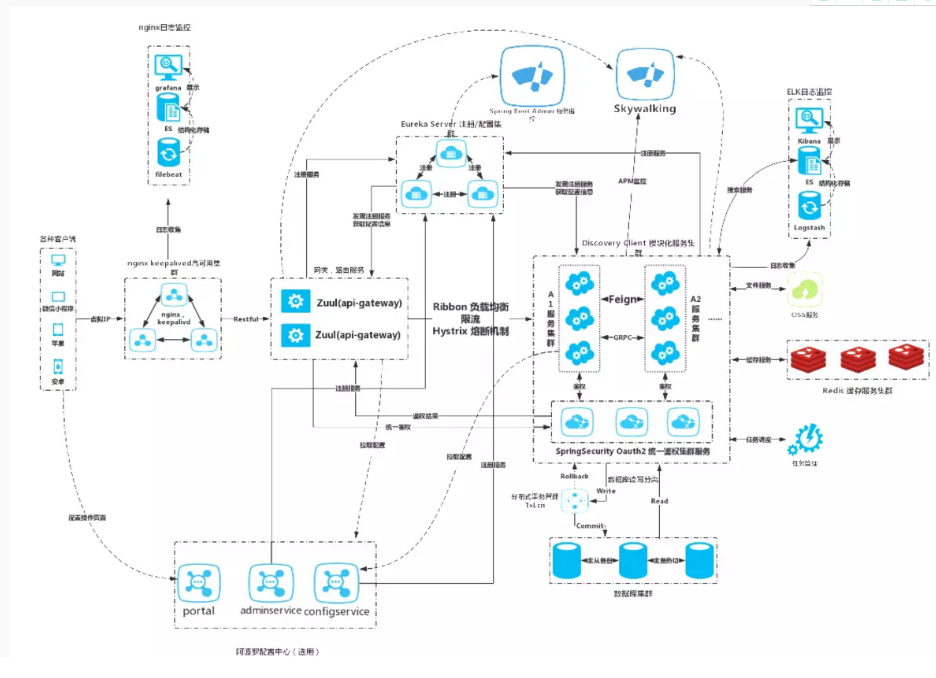
Spring Cloud Alibaba 多租户saas企业开发架构技术选型和设计方案
基于Spring Cloud Alibaba 分布式微服务高并发数据平台化(中台)思想多租户saas设计的企业开发架构,支持源码二次开发、支持其他业务系统集成、集中式应用权限管理、支持拓展其他任意子项目。 一、架构技术选型 核心框架 Spring Boot SOA Spring Cloud …...

Unity IL2CPP 游戏分析入门
一、目标 很多时候App加密本身并不难,难得是他用了一套新玩意,天生自带加密光环。例如PC时代的VB,直接ida的话,汇编代码能把你看懵。 但是要是搞明白了他的玩法,VB Decompiler一上,那妥妥的就是源码。 U…...

Python的23种设计模式(完整版带源码实例)
作者:虚坏叔叔 博客:https://xuhss.com 早餐店不会开到晚上,想吃的人早就来了!😄 Python的23种设计模式 一 什么是设计模式 设计模式是面对各种问题进行提炼和抽象而形成的解决方案。这些设计方案是前人不断试验&…...
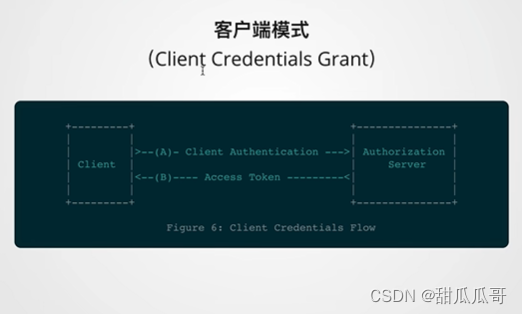
OAuth2协议
OAuth2协议流程图协议角色和流程授权所需信息授权方式授权码模式(authorization code)参数简化模式密码模式客户端模式授权方式小结流程图 协议角色和流程 user-agent:浏览器或者手机App平台 资源所有者(resourc owner࿰…...

LeetCode-115. 不同的子序列
目录动态规划题目来源 115. 不同的子序列 动态规划 1.确定dp数组(dp table)以及下标的含义 dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。 2.确定递推公式 这一类问题,基本是要分析两种情况 t[i - 1…...

kubernetes scheduler 源码解析及自定义资源调度算法实践
kubernetes scheduler 浅析 什么是kubernetes scheduler? 小到运行着几十个工作负载的 kubernetes 集群,大到运行成千上万个工作负载 kubernetes 集群,每个工作负载到底应该在哪里运行,这需要一个聪明的大脑进行指挥,…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
